M∀TH Workout

November 2023

 
  • Nov 01, 2023

11/01/2023

Morley’s Theorem: the three points of intersection of the adjacent angle trisectors of any triangle form an equilateral triangle.

image-20231101020158661

Prove:

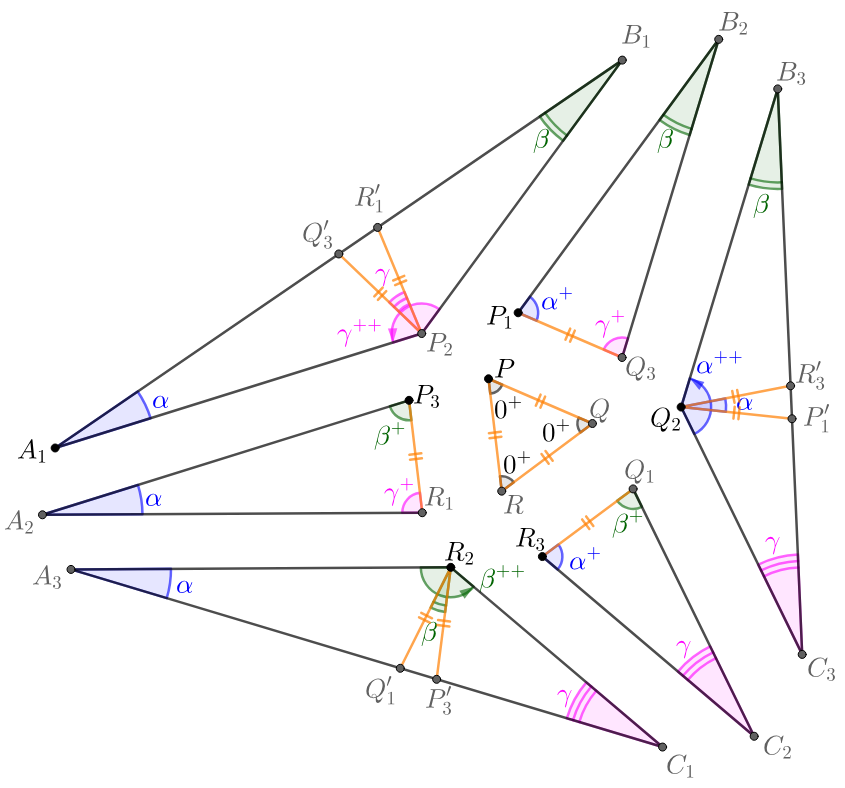
image-20231108215829814

image-20231108221245268 \(\begin{multline}\nonumber \shoveleft \text{This approval is originated from John conway.}\\ \shoveleft \text{Suppose for any angles }\alpha, \beta, \gamma \text{ such that }\alpha+\beta+\gamma=60^{\circ}\\ \shoveleft \text{ seven triangles can be constructed as above where}\\ \shoveleft 0^{+}=60^{\circ}, \alpha^{+}=\alpha+60^{\circ}, \alpha^{++}=\alpha+120^{\circ}, \text{ etc} \implies \\ \shoveleft\triangle{A_1P_2R_1'}\cong\triangle{A_2P_3R_1}\cong\triangle{A_3R_2P_3'}\\ \shoveleft \triangle{B_1P2Q_3'}\cong\triangle{B_2P_1Q_3}\cong\triangle{B_3Q_2P_1'}\\ \shoveleft \triangle{C_1R_2Q_1'}\cong\triangle{C_2R_3Q_1}\cong\triangle{C_3R_3'Q_2}\\ \shoveleft \implies P_2R_1'=P_3R_1=R_2P_3'=PR=P_2Q_3'=P_1Q_3=P_1'Q_2=PQ=R_3'Q_2=R_3Q_1=R_2Q_1'=QR\\ \shoveleft \implies \triangle{PQR} \text{ is equilateral}\implies \text{The construction is unique and determined}\\ \shoveleft \implies \text{The seven triangles can be combined to a triangle}\\ \shoveleft \implies \text{This means for any triangle, its adjacent angle trisectors form an equilateral triangle.}\blacksquare \end{multline}\)

11/02/2023

Point $E, F$ are on side $AB, AD$ of rectangle $ABCD$ such that $EF=CF, \angle{EFC}=120^{\circ}, [AEF]=M, [BCE]=N$, find $[CDF]$

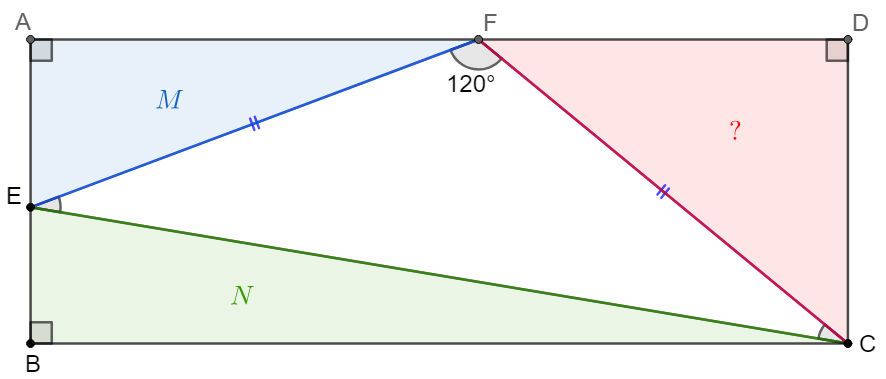
image-20231102072634776

Solve:

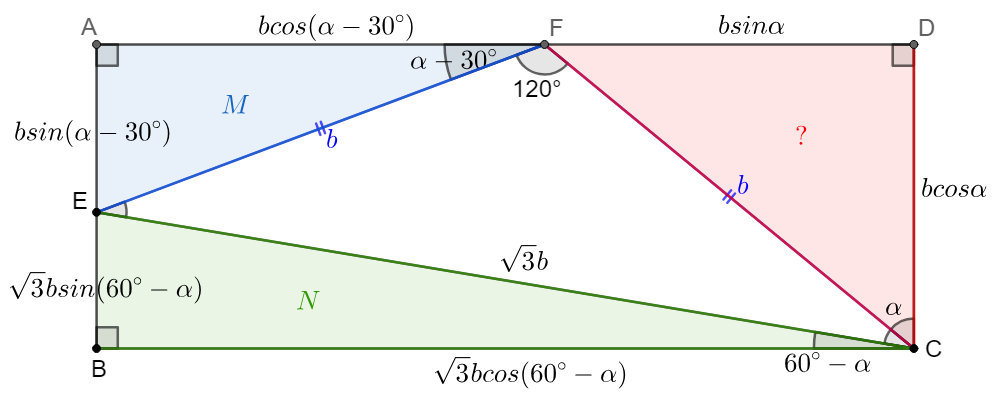image-20231102072752847 \(\begin{multline}\nonumber \shoveleft \text{Let }EF=CF=b, \angle{DCF}=\alpha \implies CE=\sqrt{3}b \\ \shoveleft \angle{AFE}=\alpha-30^{\circ}, \angle{BCE}=60^{\circ}-\alpha \implies\\ \shoveleft [AEF]=\dfrac{b^2\cdot sin(\alpha-30^{\circ})\cdot cos(\alpha-30^{\circ})}{2}\\ \shoveleft =\dfrac{b^2sin(2\alpha-60^{\circ})}{4}=M \implies sin(2\alpha-60^{\circ})=\dfrac{4M}{b^2}\\ \shoveleft \implies sin(2\alpha)cos60^{\circ}-cos(2\alpha)sin60^{\circ}=\dfrac{4M}{b^2}\\ \shoveleft [BCE]=\dfrac{3b^2\cdot sin(60^{\circ}-\alpha)\cdot cos(60^{\circ}-\alpha)}{2}\\ \shoveleft =\dfrac{3b^2sin(120^{\circ}-2\alpha)}{4}=N\implies sin(120^{\circ}-2\alpha)=\dfrac{4N}{3b^2}\\ \shoveleft \implies sin(2\alpha+60^{\circ})=\dfrac{4N}{3b^2}\implies sin(2\alpha)cos60^{\circ}+cos(2\alpha)sin60^{\circ}=\dfrac{4N}{3b^2}\\ \shoveleft [CDF]=\dfrac{b^2\cdot sin(\alpha)\cdot cos(\alpha)}{2}=\dfrac{b^2sin(2\alpha)}{4}=\dfrac{b^2(\dfrac{4M}{b^2}+\dfrac{4N}{3b^2})}{4}=\bbox[5px, border: 1px solid black]{M+\dfrac{N}{3}} \end{multline}\)

11/04/2023

$E,F$ are points on side $AD, AB$ of square $ABCD$ such that $\angle{AEF}=\angle{CEF}$,$[CBF]=4$, $[CEF]=5$, find $[CDE]$.

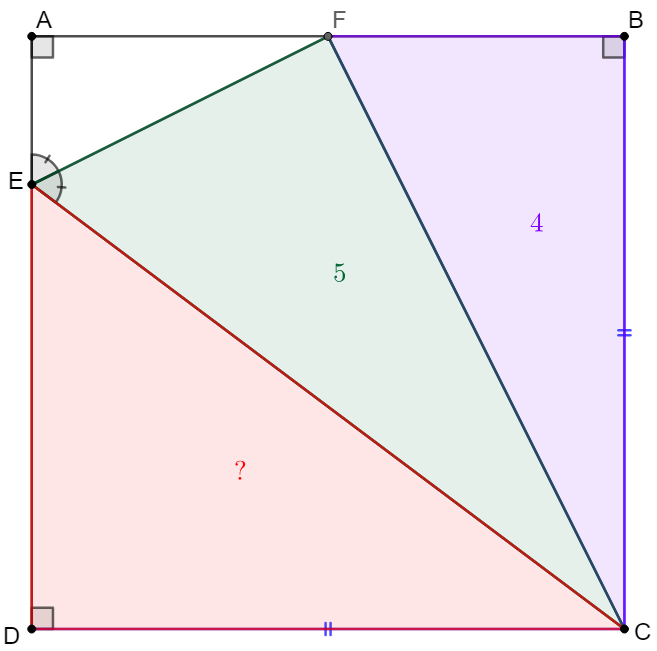
image-20231104061857887

Solve:

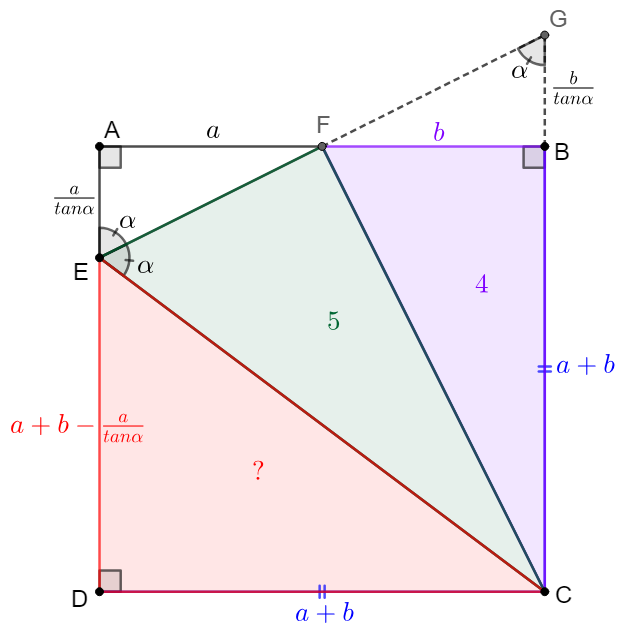image-20231105023141644 \(\begin{multline}\nonumber \shoveleft \text{Let }AF=a, BF=b, \angle{AEF}=\angle{CEF}=\alpha, \text{Extend }EF, CB \text{ and intersect at }G\\ \shoveleft \implies CD=BC=a+b, AE=\dfrac{a}{tan \alpha}, BG=\dfrac{b}{tan \alpha}, DE=a+b-\dfrac{a}{tan\alpha}\\ \shoveleft [BCF]=\dfrac{b(a+b)}{2}=4\implies \bbox[5px, border: 3px dotted red]{b(a+b)=8} \implies b < 2\sqrt{2}, [CEF]=[CEG]-[CFG]=5\\ \shoveleft \implies \dfrac{(a+b+\dfrac{b}{tan \alpha})a}{2}=5 \implies \bbox[5px, border: 3px dotted red]{tan\alpha=\dfrac{ab^2}{10b-8a}=\dfrac{b^2(8-b^2)}{18b^2-64} \gt 0} \implies 2\sqrt{2} \gt b\gt\dfrac{4a}{5}\\ \shoveleft [CDE]=\dfrac{(a+b)(a+b-\dfrac{a}{tan\alpha})}{2}=\dfrac{(a+b)(4a-b)}{b^2}=\dfrac{\dfrac{256}{b^2}-40}{b^2}\\ \shoveleft \text{For example: } a=b=2, tan\alpha=2, [CDE]=6; \text{If claim } a=b, \text{ then this is the only solution.}\\ \shoveleft \text{Otherwise, for example: }b=2.05, a=\dfrac{8}{2.05}-2.05=1.852439, b^2=4.2025, tan\alpha=1.37, [CDE]=4.977 \end{multline}\)

11/06/2023

$D$ is a point on side $BC$ of $\triangle{ABC}$ such that $\angle{DAC}=12^{\circ}, \angle{BAD}= \angle{ACB}=18^{\circ}$, show that $AB=CD$.

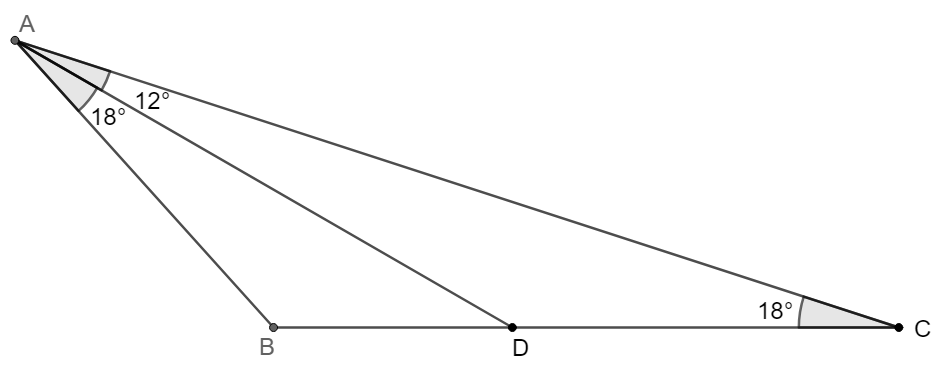
image-20231106130003362

Prove:

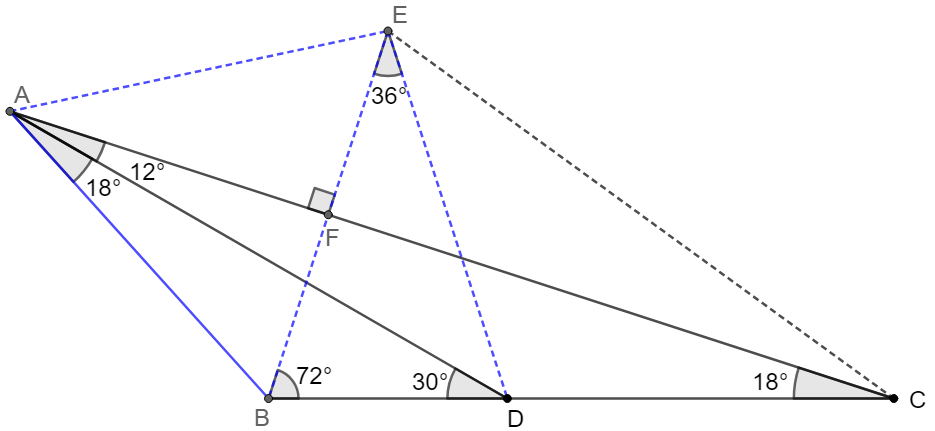image-20231106124415980 \(\begin{multline}\nonumber \shoveleft \text{Let }E \text{ be the circum-center of }\triangle{ABD}, BE \text{ and } AC \text{ intersect at } F\\ \shoveleft \angle{BAD}=18^{\circ},\angle{ADB}=30^{\circ} \implies \angle{BED}=36^{\circ}, \triangle{AEB} \text{ is equilateral}\\ \shoveleft \implies AB=AE=BE=DE, \angle{EBD}=\angle{EDB}=\dfrac{180^{\circ}-36^{\circ}}{2}=72^{\circ}\\ \shoveleft \angle{BAF}=30^{\circ}\implies AC\perp BE, BF=EF \implies \triangle{CEF}\cong\triangle{CBF}\\ \shoveleft \implies \angle{CEF}=\angle{CBF}=72{^\circ} \implies \angle{CED}=\angle{ECD}=36^{\circ}\implies CD=DE=AB\blacksquare \end{multline}\)

11/07/2023

$D$ is the mid point of side $BC$ of $\triangle{ABC}$, and $\angle{B}=30^{\circ}, \angle{C}=15^{\circ}$. Find $\angle{CAD}$.

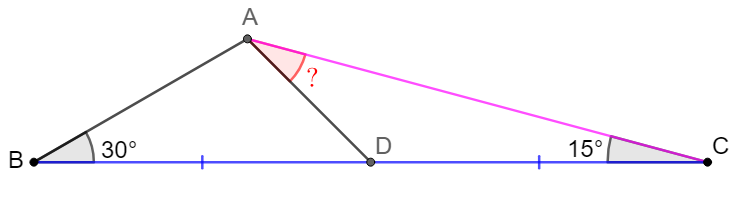
image-20231107012247835

Solve:

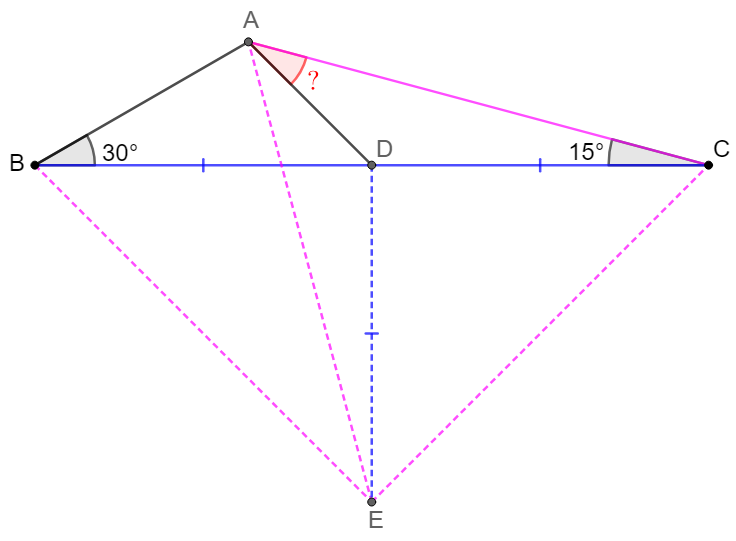image-20231107012210732 \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ the circum-center of }\triangle{ABC} \implies \\ \shoveleft AE=BE=CE, \angle{AEB}=30^{\circ}, \angle{AEC}=60^{\circ}\\ \shoveleft \implies \triangle{ACE}\text{ is equilateral}\implies AE=AC\\ \shoveleft \angle{ABE}=\angle{BAE}=75^{\circ}\implies \angle{CBE}=\angle{BCE}=45^{\circ}\\ \shoveleft \implies BD=DE=CD \implies \triangle{ADE}\cong\triangle{ADC}\\ \shoveleft \implies \angle{CAD}=\angle{EAD}=\dfrac{60^{\circ}}{2}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

11/08/2023

$\triangle{ABC}$ has $AB=6, BC=10, \angle{B}=90^{\circ}$. $D$ is midpoint of side $AB$, and $E$ is a point on $BC$ such that AE and CD intersect at $F$, $\angle{CFE}=45^{\circ}$, find $BE$.

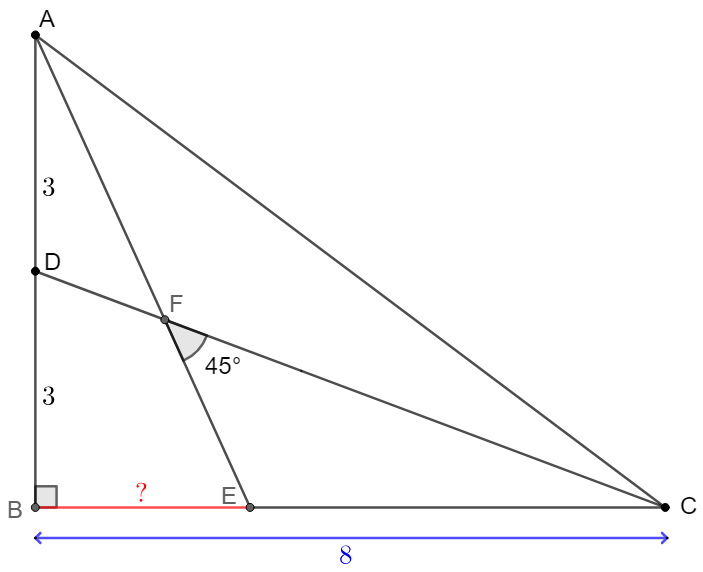
image-20231108004311680

Solve 1:

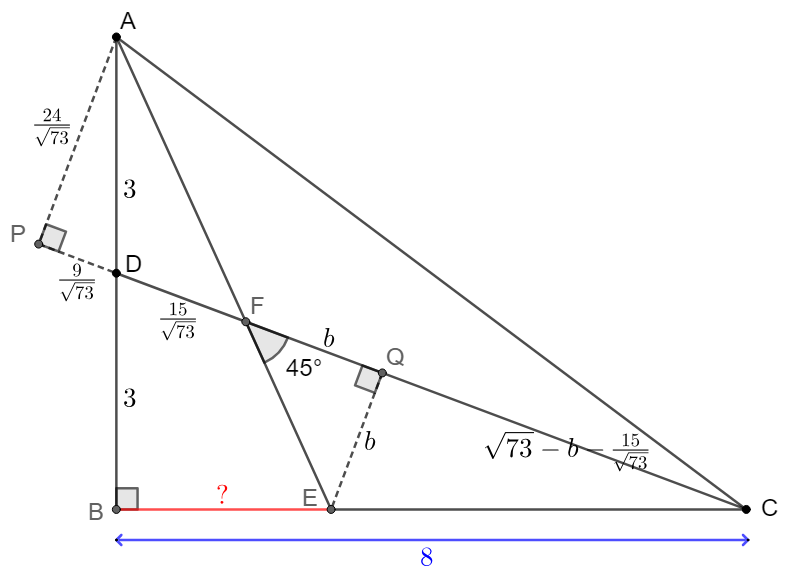image-20231108004205525 \(\begin{multline}\nonumber \shoveleft \text{Make }AP\perp CD \text{ at }P, EQ \perp CD \text{ at }Q\\ \shoveleft \triangle{ADP}\sim\triangle{CDB}\implies AP=\dfrac{24}{\sqrt{73}}, DP=\dfrac{9}{\sqrt{73}}\\ \shoveleft \implies DF=PF-PD=AP-PD=\dfrac{15}{\sqrt{73}}\\ \shoveleft \text{Let }FQ=EQ=b, CD=\sqrt{73},CQ=\sqrt{73}-\dfrac{15}{\sqrt{73}}-b\\ \shoveleft \triangle{CEQ}\sim \triangle{CDB}\implies \dfrac{\sqrt{73}-\dfrac{15}{\sqrt{73}}-b}{b}=\dfrac{8}{3}\\ \shoveleft \implies b=\dfrac{174}{11\sqrt{73}}\implies \dfrac{CE}{\dfrac{174}{11\sqrt{173}}}=\dfrac{\sqrt{73}}{3}\\ \shoveleft \implies CE=\dfrac{58}{11}\implies BE=\bbox[5px, border: 1px solid black]{\dfrac{30}{11}} \end{multline}\) Solve 2: \(\begin{multline}\nonumber \shoveleft tan(\angle{AEB})=tan(45^{\circ}+\angle{BCD})\\ \shoveleft =\dfrac{tan45^{\circ}+tan(\angle{BCD})}{1-tan45^{\circ}\cdot tan(\angle{BCD})}\\ \shoveleft =\dfrac{1+\dfrac{3}{8}}{1-\dfrac{3}{8}}=\dfrac{11}{5}=\dfrac{AB}{BE}=\dfrac{6}{BE}\\ \shoveleft \implies BE=\bbox[5px, border: 1px solid black]{\dfrac{30}{11}} \end{multline}\)

11/09/2023

In quadrilateral $ABCD$, $\angle{ABC}=38^{\circ}, \angle{CBD}=44^{\circ}, \angle{CAD}=22^{\circ},\angle{BAD}=16^{\circ}$, find $\angle{ADC}$.

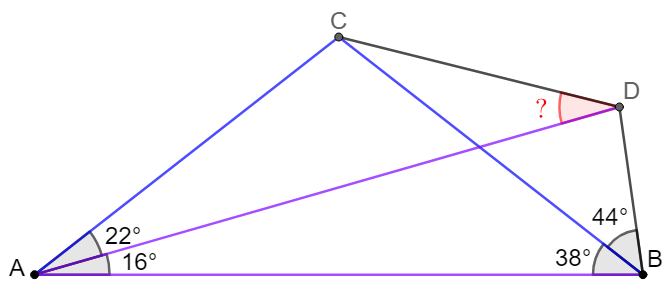
image-20231108015106962

Solve:

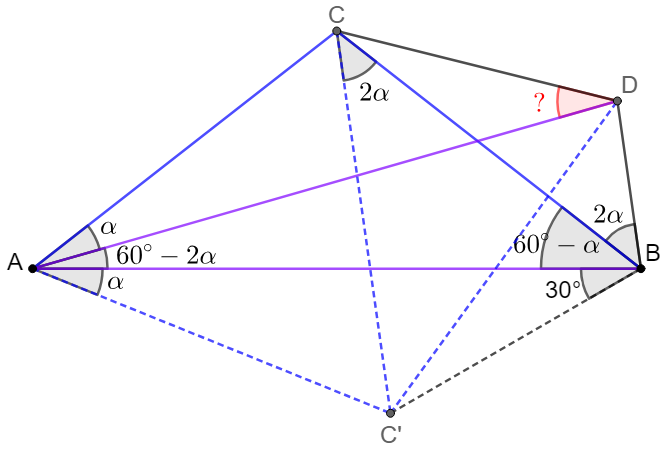image-20231108021306099 \(\begin{multline}\nonumber \shoveleft \text{It can be generalized to above figure. Easy to see }AB=AD, AC=BC.\\ \shoveleft AB=AD \implies \text{Make }C' \text{ below } AB \text{ such that }\triangle{AC'B}\cong\triangle{ACD} \implies\\ \shoveleft \angle{C'AB}=\angle{CAD}=\alpha, AC=AC'\implies \triangle{ACC'}\text{ is equilateral}\\ \shoveleft \implies CC'=AC=AC'=BC \implies C \text{ is the circum-center of }\triangle{ABC'}\\ \shoveleft \implies \angle{BCC'}=2\angle{C'AB}=2\alpha\implies \angle{CBC'}=\dfrac{180^{\circ}-2\alpha}{2}=90^{\circ}-\alpha\\ \shoveleft \implies \angle{ABC'}=90^{\circ}-\alpha-(60^{\circ}-\alpha)=30^{\circ}\implies \angle{ADC}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

11/10/2023

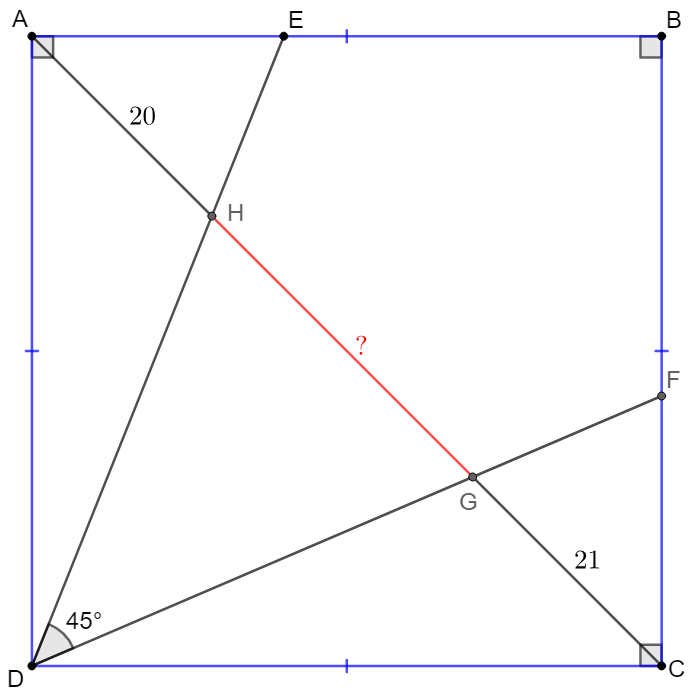
$E,F$ are on side $AB, BC$ of square $ABCD$ respectively such that $\angle{EDF}=45^{\circ}$. $DE, DF$ intersect with $AC$ at $H,G$ respectively such that $AH=20, CG=21$. Find $GH$.

image-20231108192953069

Solve:

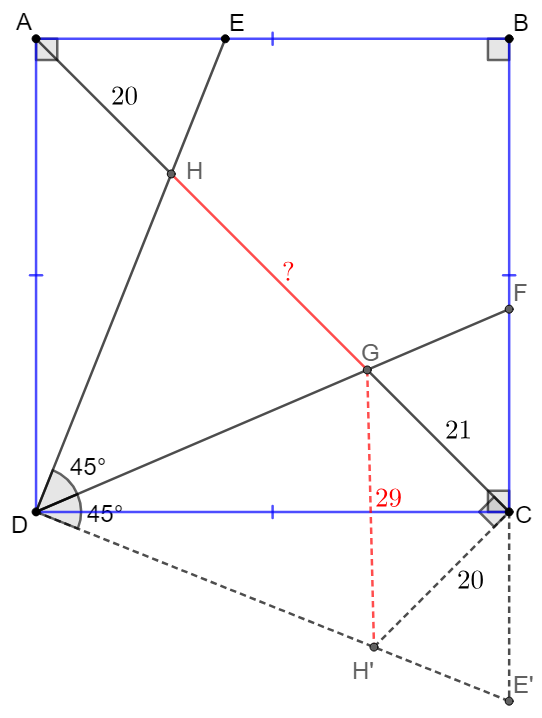
image-20231108203050122 \(\begin{multline}\nonumber \shoveleft \text{Rotate }\triangle{ADE} \text{ clockwise for } 90^{\circ}\text{ to get }\triangle{CDE'} \text{ where } H \text{ is mapped to }H'.\\ \shoveleft \implies AH=CH'=20,DH=DH', \angle{GDH'}=45^{\circ}=\angle{GDH}\\ \shoveleft \implies \triangle{DGH}\cong\triangle{DGH'}\implies GH=GH'\\ \shoveleft \text{Easy to see that }\angle{GCH'}=90^{\circ}\implies GH=GH'=\sqrt{20^2+21^2}=\bbox[5px, border: 1px solid black]{29}\\ \shoveleft \end{multline}\)

11/11/2023

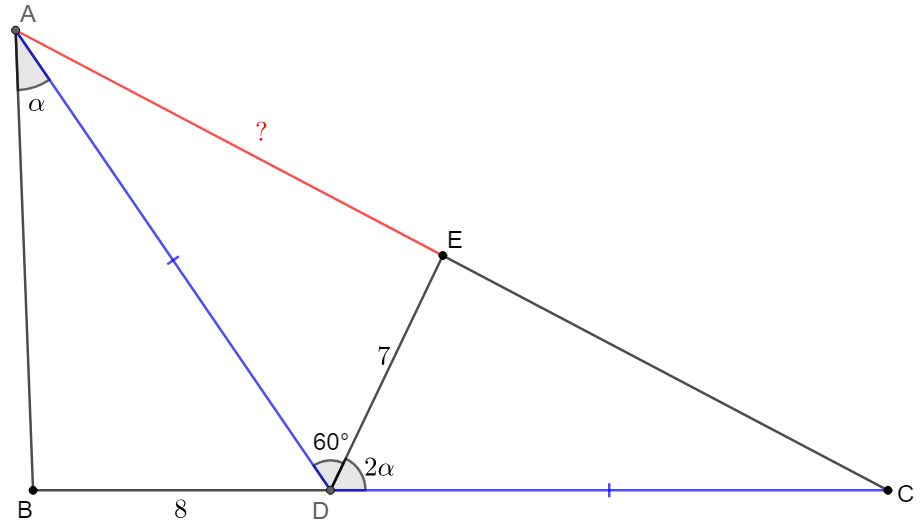
$D,E$ are points in side $BC, CA$ respectively of $\triangle{ABC}$ such that $BD=8$, $DE=7, $AD=CD$, $\angle{CDE}=2\angle{BAD}, $\angle{ADE}=60^{\circ}$, find $AE$

image-20231110223136875

Solve 1:

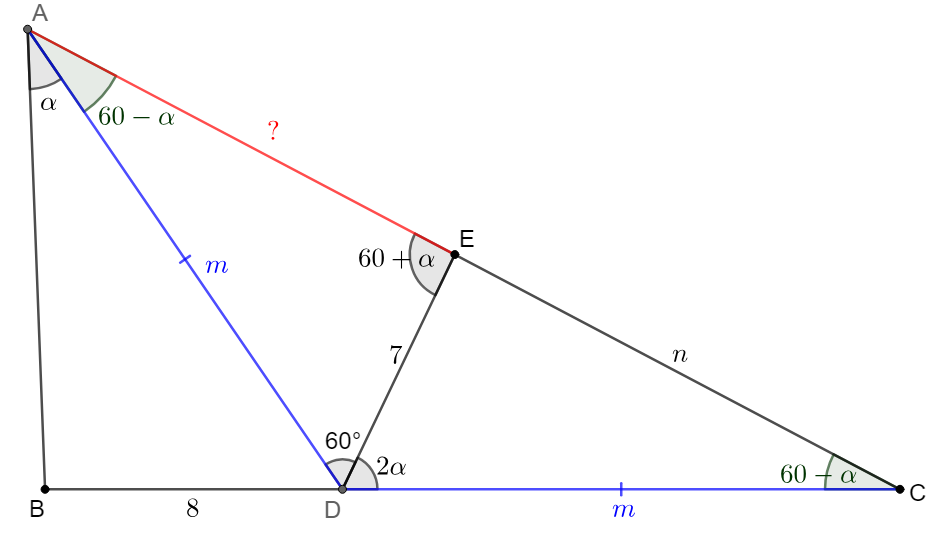
image-20231110223040915 \(\begin{multline}\nonumber \shoveleft \text{Let }AE=x, AD=CD=m, CE=n, \angle{BAD}=\alpha \implies\\ \shoveleft \angle{CDE}=2\alpha, \angle{ADB}=180^{\circ}-60^{\circ}-2\alpha=2\angle{CAD}=2\angle{ACD}\\ \shoveleft \implies \angle{CAD}=\angle{ACD}=60^{\circ}-\alpha \implies \angle{BAC}=60^{\circ}, \angle{AED}=60^{\circ}+\alpha\\ \shoveleft \implies \dfrac{7}{sin(60^{\circ}-\alpha)}=\dfrac{x}{sin60^{\circ}}=\dfrac{m}{sin(60^{\circ}+\alpha)}\\ \shoveleft \dfrac{8}{sin\alpha}=\dfrac{m}{sin(120^{\circ}-2\alpha+\alpha)}=\dfrac{m}{sin(60^{\circ}+\alpha)}\\ \shoveleft \implies \dfrac{x}{sin60^{\circ}}=\dfrac{8}{sin\alpha}=\dfrac{7}{sin60^{\circ}cos\alpha-cos60^{\circ}sin\alpha}\implies tan\alpha=\dfrac{4\sqrt{3}}{11}\\ \shoveleft \implies cos\alpha=\dfrac{11}{13}, cos\alpha=\dfrac{4\sqrt{3}}{13}\implies sin(60^{\circ}-\alpha)=\dfrac{7\sqrt{3}}{26}\\ \shoveleft \implies x=\dfrac{\dfrac{7\sqrt{3}}{2}}{\dfrac{7\sqrt{3}}{26}}=\bbox[5px, border: 1px solid black]{13} \end{multline}\) Solve 2:

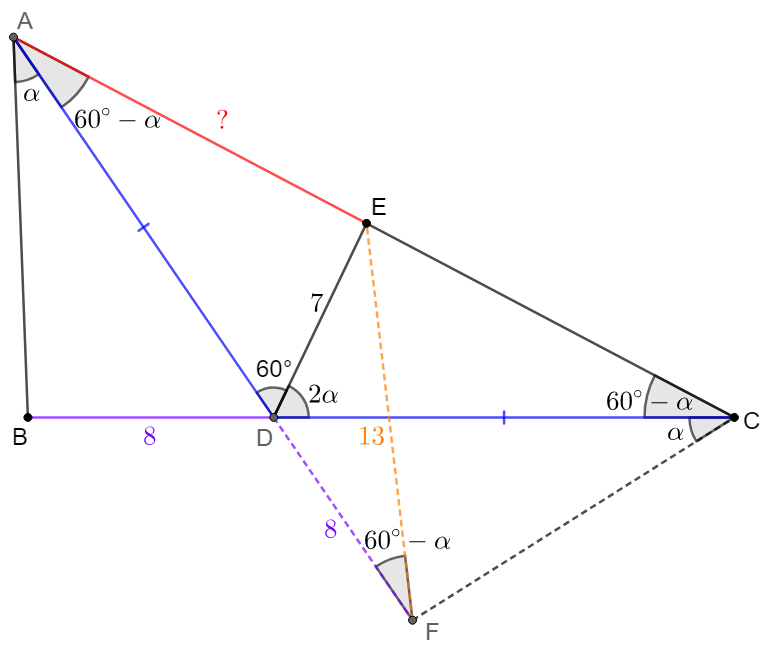image-20231110230146111 \(\begin{multline}\nonumber \shoveleft \text{Let }\angle{BAD}=\alpha \implies \angle{CDE}=2\alpha, \angle{ADB}=180^{\circ}-60^{\circ}-2\alpha=2\angle{CAD}=2\angle{ACD}\\ \shoveleft \implies \angle{CAD}=\angle{ACD}=60^{\circ}-\alpha \implies \angle{BAC}=60^{\circ}, \angle{AED}=60^{\circ}+\alpha\\ \shoveleft \text{Notice that a triangle with side length 7,8,13 has an angle } 120^{\circ}, cos120^{\circ}=\dfrac{49+64-169}{2\times7\times 8}\\ \shoveleft \text{Extend } AD \text{ to } F \text{ such that } BD=FD=8, \angle{EDF}=120^{\circ}\implies EF=13\\ \shoveleft \triangle{ABD}\cong\triangle{CFD}\implies \angle{BAD}=\angle{FCD}=\alpha\implies \angle{ECF}=60^{\circ}=\angle{ADE}\\ \shoveleft \implies CEDF \text{ is cyclic}\implies \angle{EFD}=\angle{ECD}=\angle{CAD}\implies AE=EF=\bbox[5px, border: 1px solid black]{13} \end{multline}\)

Note:

  • A triangle with sides $7, 8, 13$ has angle $120^{\circ}$

11/12/2023

$D,E,F$ are points on side $AB,BC,CA$ respectively of right angle triangle $\triangle{ABC}$ , where $DE\parallel AC, BD=18, CF=10$, find $[BEF]$

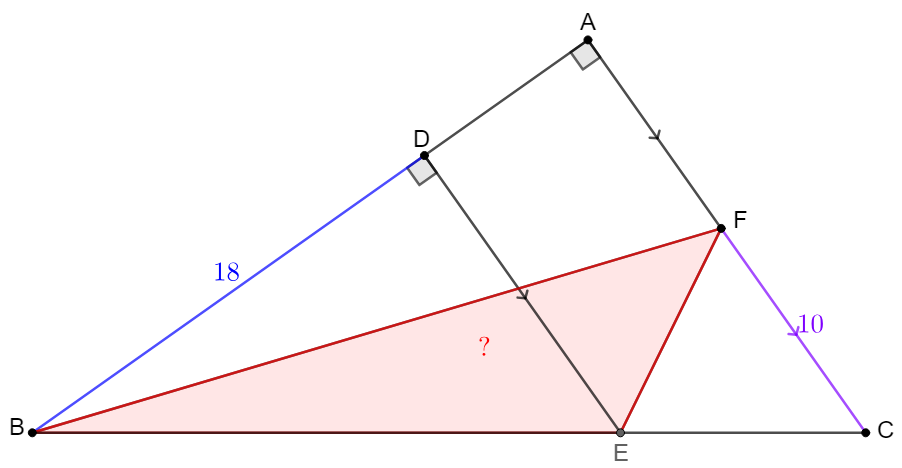
image-20231111141941543

Solve: \(\begin{multline}\nonumber \shoveleft [BEF]=[BCF]-[CEF]=\dfrac{CF \cdot AB}{2}-\dfrac{CF\cdot AD}{2}=\dfrac{CF \cdot BD}{2}=\dfrac{18\cdot10}{2}=\bbox[5px, border: 1px solid black]{90} \end{multline}\)

11/13/2023

$P,Q$ are two points outside of circle $\odot O$. $A,B,C$ are points on the circle $\odot O$. $PQ, PA, QB$ are tangent to the circle. $AC=BC$. $CP, CQ$intersect with $AB$ at $D,E$. Show that $AB=2DE$.

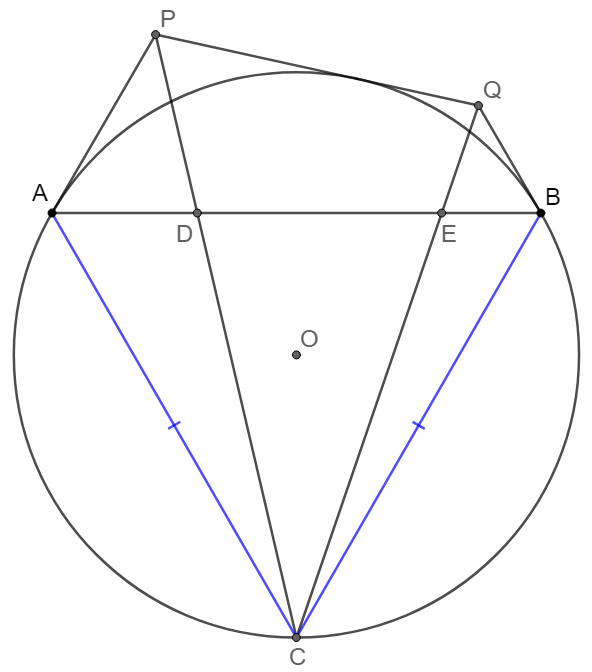
image-20231112105312922

Prove 1:

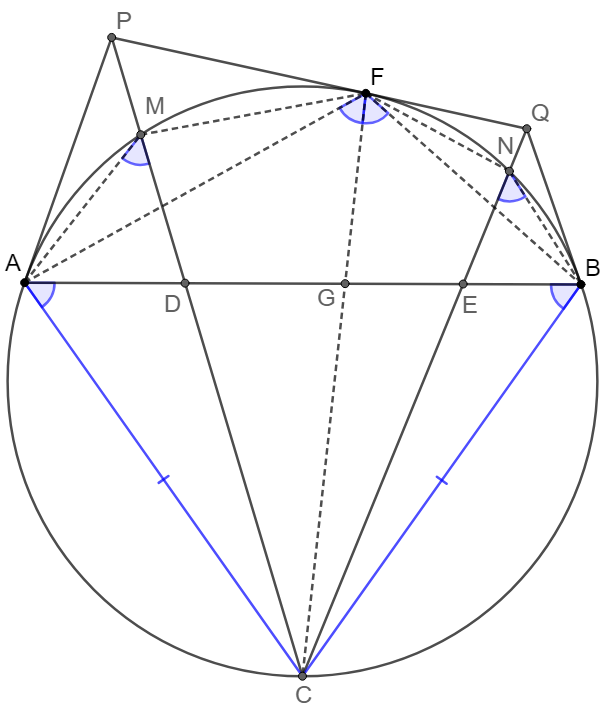image-20231114222205538 \(\begin{multline}\nonumber \shoveleft \triangle{PFM}\sim\triangle{PCF}\implies \dfrac{FM}{FC}=\dfrac{PF}{PC}=\dfrac{PA}{PC}\implies \dfrac{AM}{AC}=\dfrac{FM}{FC}\\ \shoveleft \triangle{AMC}\sim\triangle{DAC}\implies AC^2=CD\cdot CM, \dfrac{DA}{DC}=\dfrac{AM}{AC} \implies \dfrac{DA}{DC}=\dfrac{FM}{FC}\\ \shoveleft \triangle{AFC}\sim\triangle{GAC}\implies AC^2=FC \cdot CG \implies \dfrac{CD}{CG}=\dfrac{FC}{CM}\\ \shoveleft \implies \triangle{CDG}\sim\triangle{CFM}\implies \dfrac{DG}{DC}=\dfrac{FM}{FC}=\dfrac{DA}{DC}\implies DG=DA\\ \shoveleft \text{Similarly } BE=GE\implies AB=AD+DG+BE+GE=2DE\blacksquare \end{multline}\)

Prove 2 (better expressed): \(\begin{multline}\nonumber \shoveleft \triangle{PAM}\sim\triangle{PCA},\triangle{PFM}\sim\triangle{PCF}\implies \dfrac{AM}{AC}=\dfrac{PA}{PC}=\dfrac{PF}{PC}=\dfrac{FM}{FC}\\ \shoveleft \triangle{AMC}\sim\triangle{DAC}\implies \dfrac{DA}{DC}=\dfrac{AM}{AC}=\dfrac{FM}{FC}\\ \shoveleft \angle{CDG}=\angle{DAC}+\angle{ACD}=\angle{AFG}+\angle{MFA}=\angle{MFG}\\ \shoveleft \implies \triangle{CDG}\sim\triangle{CFM} \implies \dfrac{DG}{DC}=\dfrac{FM}{FC}=\dfrac{DA}{DC}\implies DA=DG\\ \shoveleft \text{Similarly } BE=GE\implies AB=AD+DG+BE+GE=2DE\blacksquare \end{multline}\)

11/14/2023

Two circles intersect at $A,D$, $B,C$ are points on one circle and $P,Q$ are points on the other. $B,P,Q,C$ are colinear. Prove that $\angle{BAP}=\angle{CDQ}$.

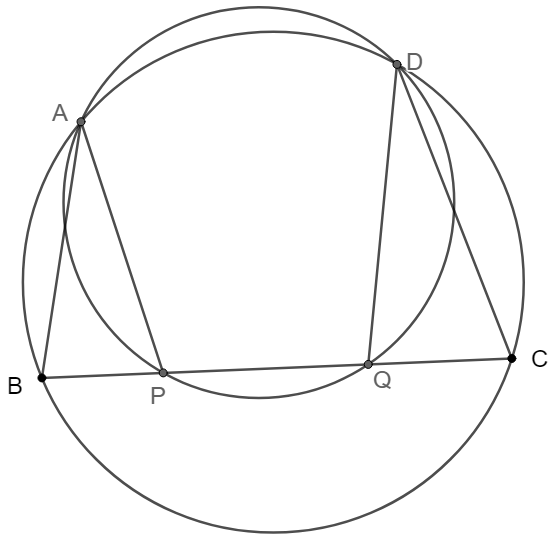
image-20231114125013991

Prove 1:

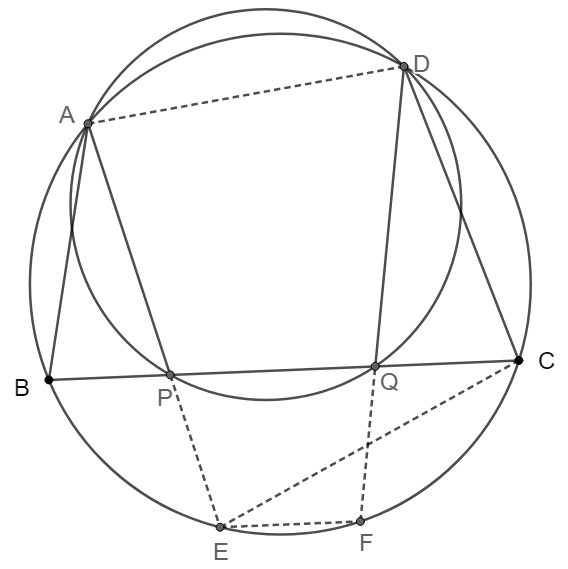image-20231114124328392 \(\begin{multline}\nonumber \shoveleft \text{Extend }AP, DQ \text{ and intersect with the circle at }E, F. \text{ Connect }CE.\\ \shoveleft APQD \text{ is cyclic }\implies \angle{PAD}=\angle{PQF}\\ \shoveleft AEFD \text{ is cyclic }\implies \angle{PAD}+\angle{EFQ}=180^{\circ}\\ \shoveleft \implies \angle{PQF}+\angle{EFQ}=180^{\circ}\implies BC\parallel EF\\ \shoveleft \implies \angle{BAP}=\angle{BCE}=\angle{CEF}=\angle{CDQ}\blacksquare \end{multline}\) Prove 2: \(\begin{multline}\nonumber \shoveleft \angle{APQ}+\angle{ADQ}=180^{\circ}=\angle{ABP}+\angle{ADC}\\ \shoveleft \implies \angle{APQ}-\angle{ABP}=\angle{ADC}-\angle{ADQ}\\ \shoveleft \implies \angle{BAP}=\angle{CDQ}\blacksquare \end{multline}\)

11/15/2023

$D,F,G$ are points on side $AC,AB,BC$ of $\triangle{ABC}$ respectively. extended $DF, CB$ intersect at $E$, extended $DG,AB$ intersect at $F$, $[AEF]=M$, $[BEF]=N$, $[BFG]=P$,$[CFG]=Q$, find $X=[ADF]$,$Y=[BFDG]$,$Z=[CDG]$

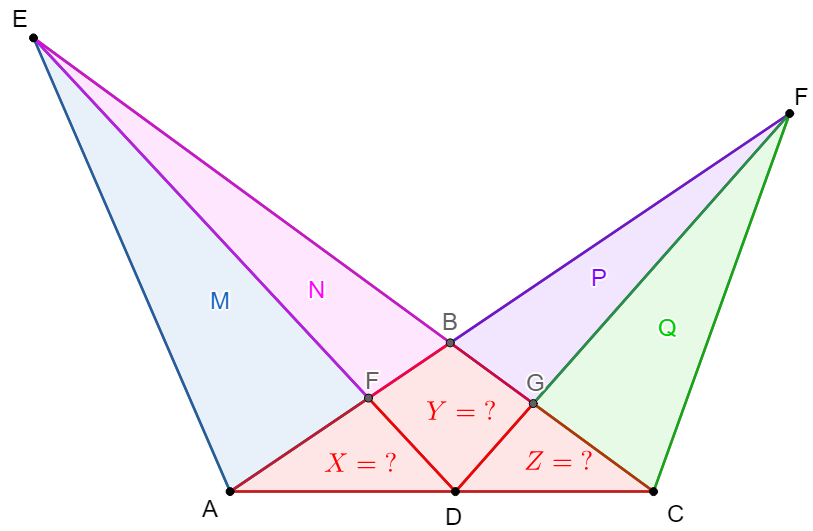
image-20231114140726225

solve:

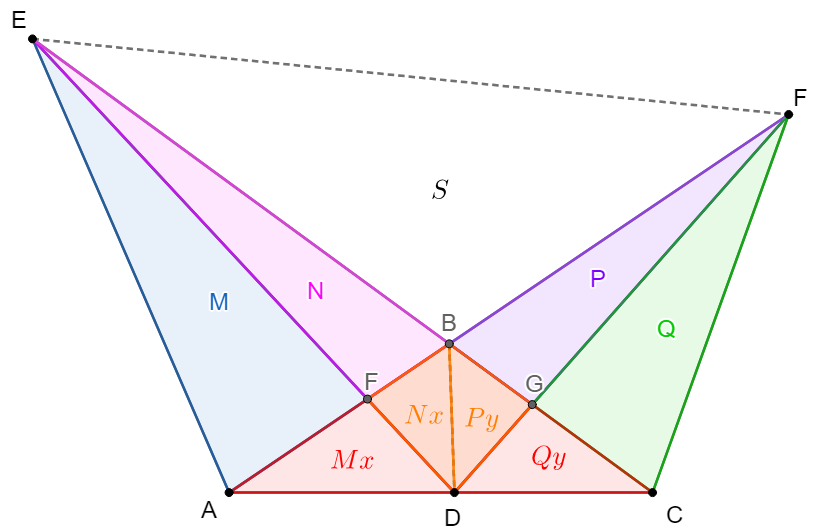image-20231115162101075 \(\begin{multline}\nonumber \shoveleft \dfrac{P+Q}{S}=\dfrac{(M+N)x+(P+Q)y}{M+N}\implies S=\dfrac{(P+Q)(M+N)}{(M+N)x+(P+Q)y}\\ \shoveleft \dfrac{Mx}{M}=x=\dfrac{P+Nx+Py}{S+N}\implies Sx=(1+y)P \implies S=\dfrac{(1+y)P}{x}\\ \shoveleft \dfrac{Qy}{Q}=y=\dfrac{N+Nx+Py}{S+P}\implies Sy=(1+x)N \implies S=\dfrac{(1+x)N}{y}\\ \shoveleft \implies \bbox[5px, border: 2px dotted red]{\dfrac{(1+y)P}{x}=\dfrac{(1+x)N}{y}=S}\\ \shoveleft \dfrac{(1+x)M}{(1+x)N+(P+Q)y}=\dfrac{(1+y)P+(M+N)x}{(1+y)Q}=\dfrac{(M+N)x}{(P+Q)y}\\ \shoveleft \implies \dfrac{(1+x)M}{(S+P+Q)y}=\dfrac{(S+M+N)x}{(1+y)Q}=\dfrac{(M+N)x}{(P+Q)y}\implies \\ \shoveleft x=\dfrac{M(P+Q)}{S(M+N)+N(P+Q)}, y=\dfrac{Q(M+N)}{S(P+Q)+P(M+N)}\implies \\ \shoveleft (1+x)N(P+Q)+P(M+N)y=Q(M+N)\\ \shoveleft (1+y)P(M+N)+N(P+Q)x=M(P+Q)\\ \shoveleft \implies \bbox[5px, border: 2px dotted red]{N(P+Q)x+P(M+N)y=MQ-NP}\\ \shoveleft \text{The answer is given by solving equation system: }\\ \shoveleft \begin{cases} x(1+x)N=y(1+y)P\\ N(P+Q)x+P(M+N)y=MQ-NP \end{cases} \\ \shoveleft \text{The result is: }X=Mx, Y=Nx+Py,Z=Qy \end{multline}\) Solve 2: \(\begin{multline}\nonumber \shoveleft placeholder \end{multline}\)

11/16/2023

Three circles radius as $6,7,8$ are externally tagent to each other. The fourth large circle has the three circles inscribed is tagent to all of them. Find the radius of this larger circle.

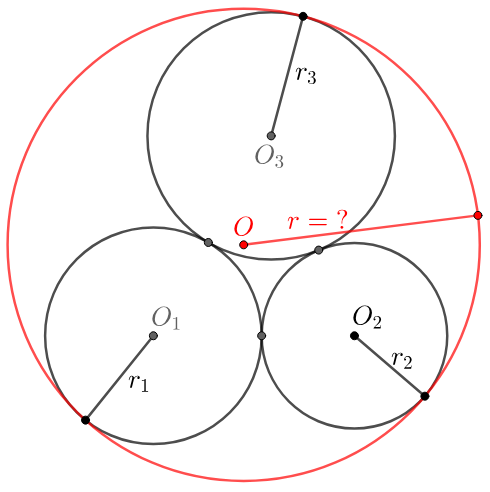
image-20231116133223805

Solve: \(\begin{multline}\nonumber \shoveleft \text{Applying Descarte's Theorem: }\\ \shoveleft (\dfrac{1}{r_1}+\dfrac{1}{r_2}+\dfrac{1}{r_3}-\dfrac{1}{r})^2=2(\dfrac{1}{r_1^2}+\dfrac{1}{r_2^2}+\dfrac{1}{r_3^2}+\dfrac{1}{r^2})\\ \shoveleft \text{Let }A=\prod_{cyc}r_i, B=\sum_{cyc}{r_ir_j},C=B^2-2\sum_{cyc}{r_i^2r_j^2}\\ \shoveleft \implies r=\bbox[5px, border: 1px solid black]{\dfrac{A}{C}\Big(B+\sqrt{B^2+C}\Big)}\\ \shoveleft \text{For }r_1=6, r_2=7, r_3=8, A=336, B=146, C=6908\\ \shoveleft \implies r=\dfrac{336}{6908}\Big(146+\sqrt{146^2+6908}\Big)=\bbox[5px, border: 1px solid black]{\dfrac{168}{11}} \end{multline}\)

11/17/2023

$D$ is a point inside $\triangle{ABC}$ such that $\angle{BAD}=10^{\circ}$, $\angle{ABD}=\angle{CAD}=20^{\circ}$, $\angle{CBD}=60^{\circ}$, find $\angle{BCD}$.

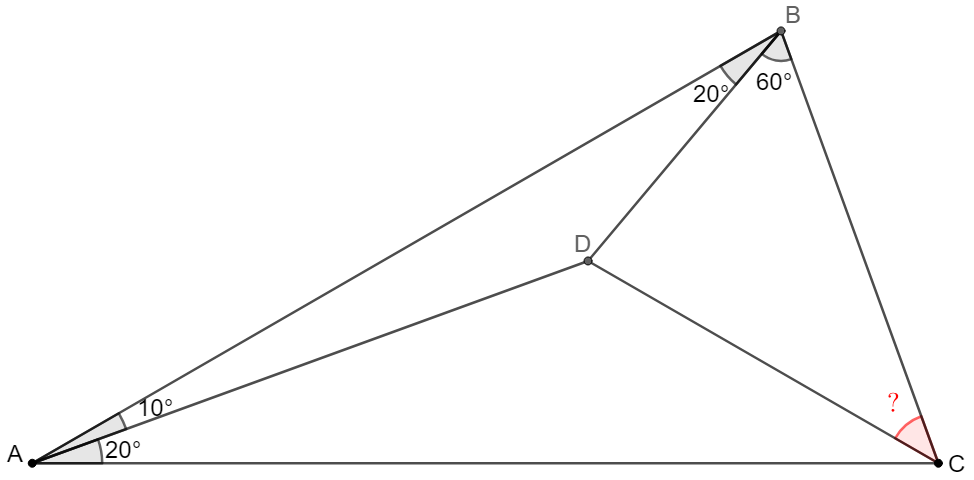
image-20231118020431371

Solve:

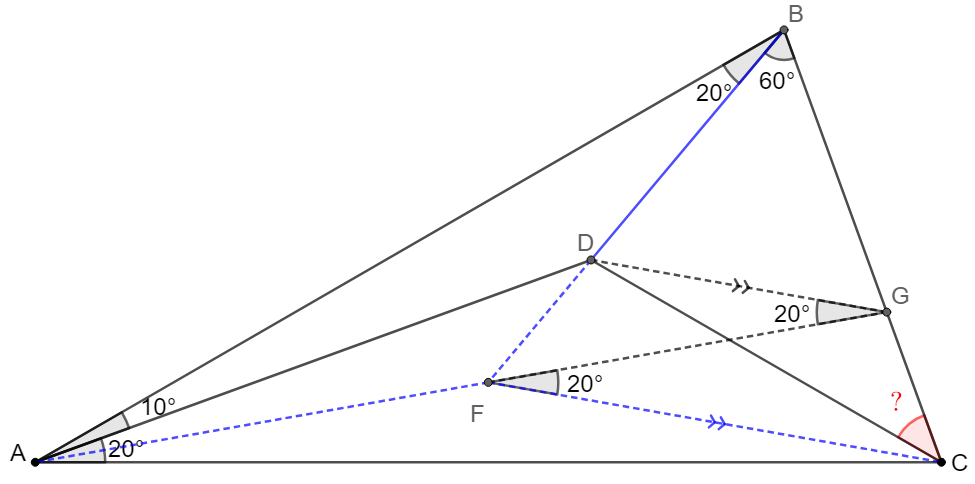image-20231118020341011 \(\begin{multline}\nonumber \shoveleft \text{Let }F \text{ be the circumcenter of } \triangle{ABC} \implies\\ \shoveleft AF=BF=CF, \angle{BFC}=2\angle{BAC}=60^{\circ}=\angle{DBC}\\ \shoveleft \implies B,D,F \text{ are colinear}, \triangle{BFC}\text{ is equilateral}\\ \shoveleft \implies \angle{FAB}=\angle{FBA}=20^{\circ}\implies \angle{FAD}=\angle{BAD}=10^{\circ}\\ \shoveleft \implies \text{Extend }AF \text{ and intersect } BC \text{ at }G \implies \angle{AGB}=80^{\circ}=\angle{ABG}\\ \shoveleft \implies AB=AG \implies \triangle{BAD}\cong\triangle{GAD}\implies \angle{DGF}=20^{\circ}, BD=BG\\ \shoveleft \implies \triangle{BDG}\text{ is equilateral} \implies DG\parallel CF\implies CGDF \text{ is cyclic}\\ \shoveleft \implies \angle{CDG}=\angle{CFG}=\angle{DGF}=20^{\circ}\\ \shoveleft \implies \angle{BCD}=180^{\circ}-60^{\circ}-60^{\circ}-20^{\circ}=\bbox[5px, border: 1px solid black]{40^{\circ}} \end{multline}\)

11/18/2023

$\displaystyle\sum_{n=1}^{\infty}{\dfrac{1}{n^4}}=?$

Solve 1: \(\begin{multline}\nonumber \shoveleft \text{Recall that the Fourier series for a } 2\pi \text{-periodic function }f \text{ has the complex form}\\ \shoveleft S(x)=\displaystyle \sum_{n=-\infty}^{\infty}{c_ne{inx}}, \quad c_n=(f, e_n)=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{f(x)e^{-inx}dx}\\ \shoveleft \text{The convergence theorem states that if }f: \mathbb{R} \rightarrow \mathbb{R} \text{ is continuous}, 2\pi \text{-periodic,}\\ \shoveleft \text{and piecewise, then the series converges uniformly on } \mathbb{R}\text{, and }S(x)=f(x) \text{ for all }x \in \mathbb{R}.\\ \shoveleft \text{Taking the limit }N\rightarrow \infty \text{ in the generalized Pythagoream theorem will get}\\ \shoveleft \sum_{n=-\infty}^{\infty}{|c_n|^2}=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{|f(x)|^2dx}. \text{ This is called Parseval's identity.}\\ \shoveleft \text{To apply this identity, we define }f(x)=x^2 \text{ for } x \in[-\pi, \pi], \text{ then}\\ \shoveleft c_n=(f, e_n)=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{x^2e^{-inx}dx}=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{x^2(cos(nx)-isin(nx))dx}=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{x^2cos(nx)dx}\\ \shoveleft \implies 2\pi c_n=2\int_{0}^{\pi}{x^2cos(nx)dx}=2\Big(x^2\dfrac{sin(nx)}{n}-2x\dfrac{-cos(nx)}{n^2}+2\dfrac{-sin(nx)}{n^3}\Big)\bigg|_{0}^{\pi}=\dfrac{4\pi cos(n\pi)}{n^2}\\ \shoveleft \implies c_n=2\dfrac{(-1)^n}{n^2} \text{for } n \ne 0. \text{ For } n=0 \text{ we have: } c_0=(f, e_0)=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{x^2dx}=\dfrac{1}{\pi}\int_{0}^{\pi}{x^2dx}=\dfrac{\pi^2}{3}\\ \shoveleft c_n=-c_n \implies \text{for all }x\in [-\pi, \pi], x^2=c_0+\sum_{n=1}^{\infty}{c_n(e^{inx}+e^{-inx})}=\dfrac{\pi^2}{3}+\sum_{n=1}^{\infty}{4\dfrac{(-1)^n}{n^2}cos(nx)}\\ \shoveleft \text{Furthermore, Parseval's identity says that }|c_0|^2+\sum_{n=1}^{\infty}{(|c_n|^2+|-c_n|^2)}=\dfrac{1}{2\pi}\int_{-\pi}^{\pi}{|x^2|^2dx}\\ \shoveleft \implies \dfrac{\pi^4}{9}+2\sum_{n=1}^{\infty}{\frac{4}{n^4}}=\dfrac{1}{\pi}\int_{0}^{\pi}{x^4dx}=\dfrac{1}{\pi}\dfrac{\pi^5}{5}=\dfrac{\pi^4}{5}\implies \zeta(4)=\sum_{n=1}^{\infty}{\dfrac{1}{n^4}}=\dfrac{\pi^4}{8}(\dfrac{1}{5}-\dfrac{1}{9})=\bbox[5px, border: 1px solid black]{\dfrac{\pi^4}{90}} \end{multline}\) Solve 2: \(\begin{multline}\nonumber \shoveleft \text{Without using } Parseval's identity \text{, starting from Euler's approach:}\\ \shoveleft \text{Euler devides the infinite power series } sin\theta=\frac{\theta}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+... \text{ by }y=sin\theta:\\ \shoveleft 0=1-\dfrac{\theta}{1!y}+\dfrac{\theta^3}{3!y}-\dfrac{\theta^5}{5!y}+\dfrac{\theta^7}{7!y}-...=(1-\dfrac{\theta}{\theta_0})(1-\dfrac{\theta}{\theta_1})(1-\dfrac{\theta}{\theta_2})(1-\dfrac{\theta}{\theta_3})(1-\dfrac{\theta}{\theta_4})...\\ \shoveleft \text{where the infinitely many roots }\theta_0, \theta_1, \theta_2,...\text{ are the angles for which }sin\theta_n=y=sin\theta.\\ \shoveleft \text{Coefficients on each power of }\theta \text{ on both sides gives the respective powers of }\theta, \theta^2, \theta^3, \theta^4:\\ \shoveleft \text{Then check the values for }y=sin\theta=1, \theta_0=\frac{\pi}{2}:\\ \shoveleft \dfrac{1}{1!y}=\dfrac{1}{\theta_0}+\dfrac{1}{\theta_1}+\dfrac{1}{\theta_2}+\dfrac{1}{\theta_3}+...=\dfrac{1}{\theta_0}+\dfrac{1}{\pi-\theta_0}+\dfrac{1}{-\pi-\theta_0}+\dfrac{1}{-2\pi+\theta_0}+\dfrac{1}{2\pi+\theta_0}+...\implies \\ \shoveleft 1=\dfrac{1}{\tfrac{\pi}{2}}+\dfrac{1}{\pi-\tfrac{\pi}{2}}+\dfrac{1}{-\pi-\tfrac{\pi}{2}}+\dfrac{1}{-2\pi+\tfrac{\pi}{2}}+\dfrac{1}{2\pi+\tfrac{\pi}{2}}+...=\dfrac{2}{\pi}\Big(\dfrac{1}{1}+\dfrac{1}{1}-\dfrac{1}{3}-\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{5}-...\Big)\\ \shoveleft 0=\dfrac{1}{\theta_0\theta_1}+\dfrac{1}{\theta_0\theta_2}+\dfrac{1}{\theta_0\theta_3}+\dfrac{1}{\theta_0\theta_4}+\dfrac{1}{\theta_1\theta_2}+\dfrac{1}{\theta_1\theta_3}+\dfrac{1}{\theta_1\theta_4}+\dfrac{1}{\theta_2\theta_3}+\dfrac{1}{\theta_2\theta_4}+\dfrac{1}{\theta_3\theta_4}...\\ \shoveleft -\dfrac{1}{3!y}=\dfrac{1}{6}=\dfrac{1}{\theta_0\theta_1\theta_2}+\dfrac{1}{\theta_0\theta_1\theta_3}+\dfrac{1}{\theta_0\theta_1\theta_4}+\dfrac{1}{\theta_0\theta_2\theta_3}+\dfrac{1}{\theta_0\theta_2\theta_4}+\dfrac{1}{\theta_0\theta_3\theta_4}+\dfrac{1}{\theta_1\theta_2\theta_3}+\dfrac{1}{\theta_1\theta_2\theta_4}+...\\ \shoveleft 0=\dfrac{1}{\theta_0\theta_1\theta_2\theta_3}+\dfrac{1}{\theta_0\theta_1\theta_2\theta_4}+\dfrac{1}{\theta_0\theta_1\theta_3\theta_4}+\dfrac{1}{\theta_0\theta_2\theta_3\theta_4}+\dfrac{1}{\theta_1\theta_2\theta_3\theta_4}+...\\ \shoveleft \text{Euler expresses the sum of fourth powers of terms in an arbitrary series }a,b,c,d,e,... \text{ as}\\ \shoveleft a^4+b^4+c^4+d^4+e^4+... = \alpha^4 -4\alpha^2 \beta +4\alpha\gamma + 2\beta^2-4\delta \text{, where} \\ \shoveleft \alpha=a+b+c+d+e+...=\dfrac{2}{\pi}\Big(1+1-\dfrac{1}{3}-\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{5}-...\Big) \implies\\ \shoveleft a=\dfrac{1}{\theta_0}=\dfrac{2}{\pi}=b=\dfrac{1}{\theta_1}, c=\dfrac{1}{\theta_2}=-\dfrac{2}{\pi}\dfrac{1}{3}=-\dfrac{2}{3\pi}=d=\dfrac{1}{\theta_4}, e=\dfrac{1}{\theta_5}=\dfrac{2}{\pi}\dfrac{1}{5}=\dfrac{2}{5\pi},...\\ \shoveleft \beta=ab+ac+ad+ae+bc+bd+be+cd+ce+de+... \\ \shoveleft \gamma=abc+abd+abe+acd+ace+ade+bcd+bce+cde+... \\ \shoveleft \delta=abcd+abce+abde+acde+bcde+... \\ \shoveleft \implies a^4+b^4+c^4+d^4+e^4+...=\dfrac{16}{\pi^4}\Big(1+1+\dfrac{1}{3^4}+\dfrac{1}{3^4}+\dfrac{1}{5^4}+\dfrac{1}{5^4}+...\Big)=1^4-\dfrac{4}{6}=\dfrac{1}{3}\\ \shoveleft \implies \sum_{n=1,3,5,...}^{\infty}{\dfrac{1}{n^4}}=\dfrac{1}{1^4}+\dfrac{1}{3^4}+\dfrac{1}{5^4}+\dfrac{1}{7^4}+...=\dfrac{\pi^4}{96}\\ \shoveleft \implies \sum_{n=1,2,3...}^{\infty}{\Big(\dfrac{1}{1^4}+\dfrac{1}{2^4}+\dfrac{1}{3^4}+\dfrac{1}{4^4}+...\Big)}=\dfrac{16}{15}\dfrac{15}{16}\Big(\dfrac{1}{1^4}+\dfrac{1}{2^4}+\dfrac{1}{3^4}+\dfrac{1}{4^4}+...\Big)\\ \shoveleft =\dfrac{16}{15}\Big(1-\dfrac{1}{2^4}\Big)\Big(\dfrac{1}{1^4}+\dfrac{1}{2^4}+\dfrac{1}{3^4}+\dfrac{1}{4^4}+...\Big)\\ \shoveleft =\dfrac{16}{15}\Big(\dfrac{1}{1^4}+\dfrac{1}{2^4}+\dfrac{1}{3^4}+\dfrac{1}{4^4}+...-\dfrac{1}{2^4}-\dfrac{1}{4^4}-\dfrac{1}{6^4}-\dfrac{1}{8^4}-...\Big)\\ \shoveleft =\dfrac{16}{15}\Big(\dfrac{1}{1^4}+\dfrac{1}{3^4}+\dfrac{1}{5^4}+\dfrac{1}{7^4}+...\Big)=\dfrac{16}{15}\dfrac{\pi^4}{96}=\bbox[5px, border: 1px solid black]{\dfrac{\pi^4}{90}} \end{multline}\) Note:

11/20/2023

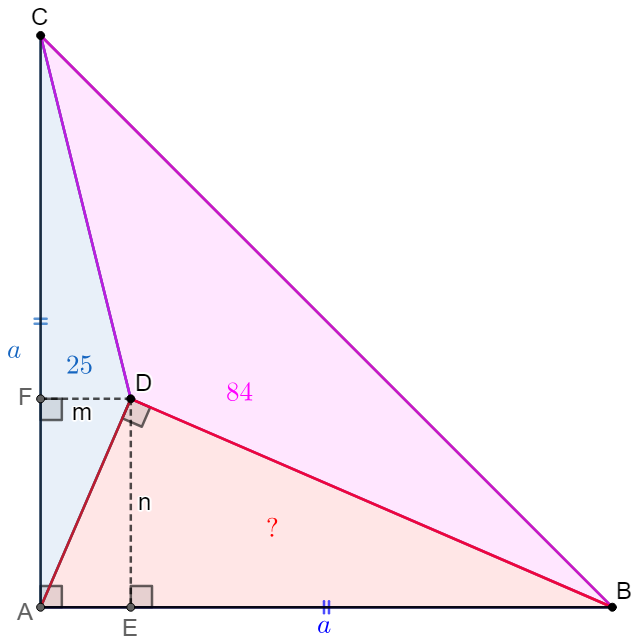
$AB=AC, \angle{CAB}=90^{\circ}$ for $\triangle{ABC}$. $D$ is inside $\triangle{ABC}$ such that $\angle{ADB}=90^{\circ}$, $[ADC]=25$, $[BCD]=84$, find $[ADB]$.

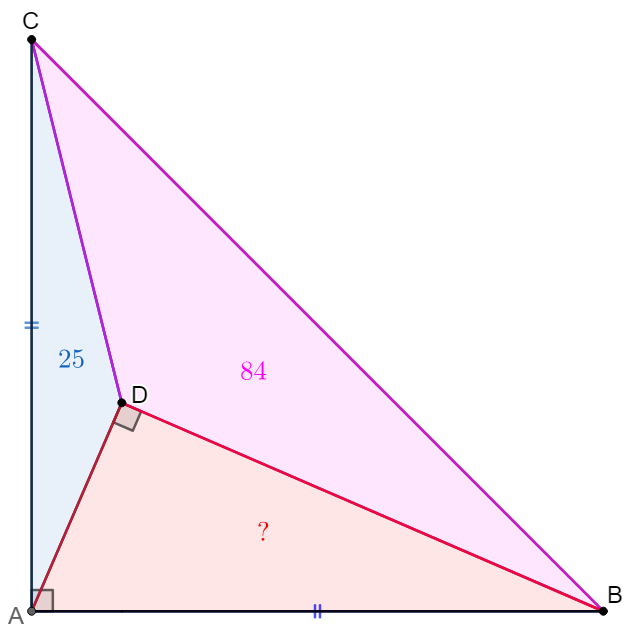
image-20231120134852451

Solve:

image-20231120140142842 \(\begin{multline}\nonumber \shoveleft \text{Make } DE\perp AB \text{ at }E, DF\perp AC \text{ at }F, \text{ let }AB=AC=a, DF=m, DE=n\\ \shoveleft \implies AE=m, BE=a-m, n^2=m(a-m), \dfrac{am}{2}=25, \dfrac{a^2}{2}-\dfrac{am}{2}-\dfrac{an}{2}=84\\ \shoveleft \implies am=50, an=a^2-218, 2500+(a^2-218)^2=50a^2 \implies a^4-486a^2+50024=0\\ \shoveleft \implies a^2=338 \text{ or } 148 \implies a=\sqrt{338} \text{ (}a=\sqrt{148} \text{ is abandoned}) \implies [ABD]=\dfrac{an}{2}=\bbox[5px, border: 1px solid black]{60} \end{multline}\) Solve 2:

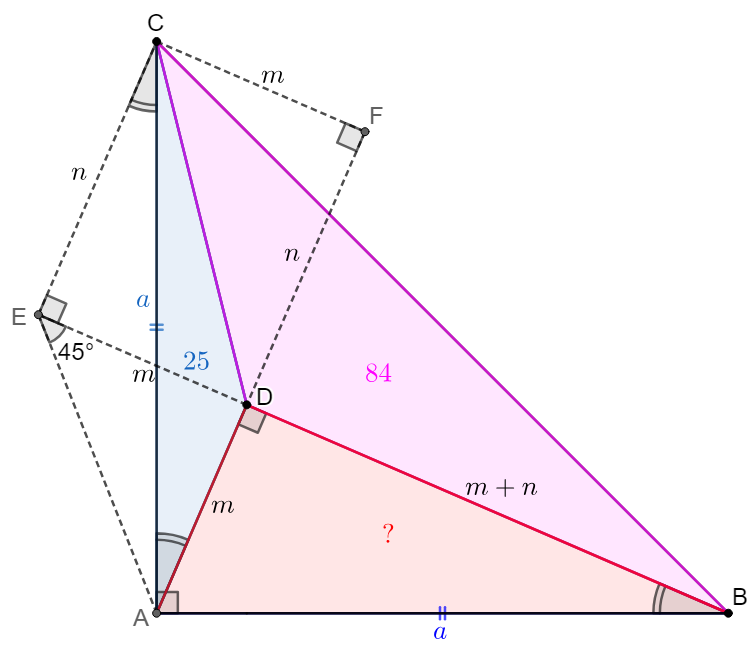image-20231120125805676 \(\begin{multline}\nonumber \shoveleft \text{Make } CE\perp DB \text{ at }E, CF\perp AD \text{ at }F, \text{ let }AB=AC=a, DE=m, DF=n\\ \shoveleft \implies \angle{ABD}=\angle{CAD}=\angle{ACE}\implies ABCE\text{ is cyclic}\implies \angle{AEB}=45^{\circ}\\ \shoveleft \implies AD=m=CF \implies \triangle{ACF}\cong\triangle{BAD}\implies BD=m+n\\ \shoveleft \implies \dfrac{m^2}{2}=25 \implies m=5\sqrt{2} \implies \dfrac{(m+n)n}{2}=84 \implies n=7\sqrt{2}\\ \shoveleft \implies [ABD]=\dfrac{m(m+n)}{2}=\bbox[5px, border: 1px solid black]{60} \end{multline}\)

11/21/2023

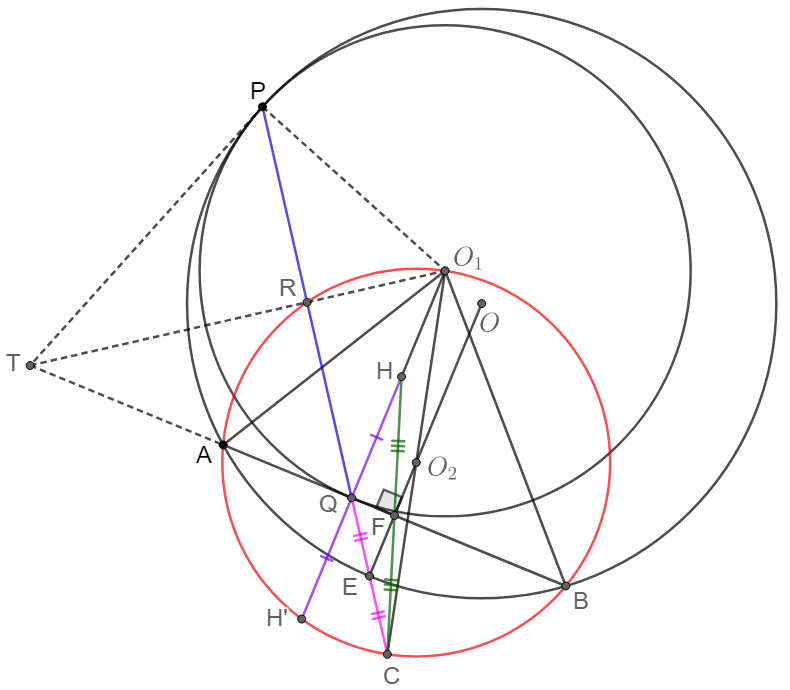
$\odot{O_1}, \odot{O_2}$ are two circles tangent to each other at $E$ and are inscribed in segment of $\odot{O}$ and its secant $AB$. $P,Q$ are the tangent points of $\odot{O_1}, \odot{O_2}$ on $AB$, show that $\angle{AEP}=\angle{BEQ}$.

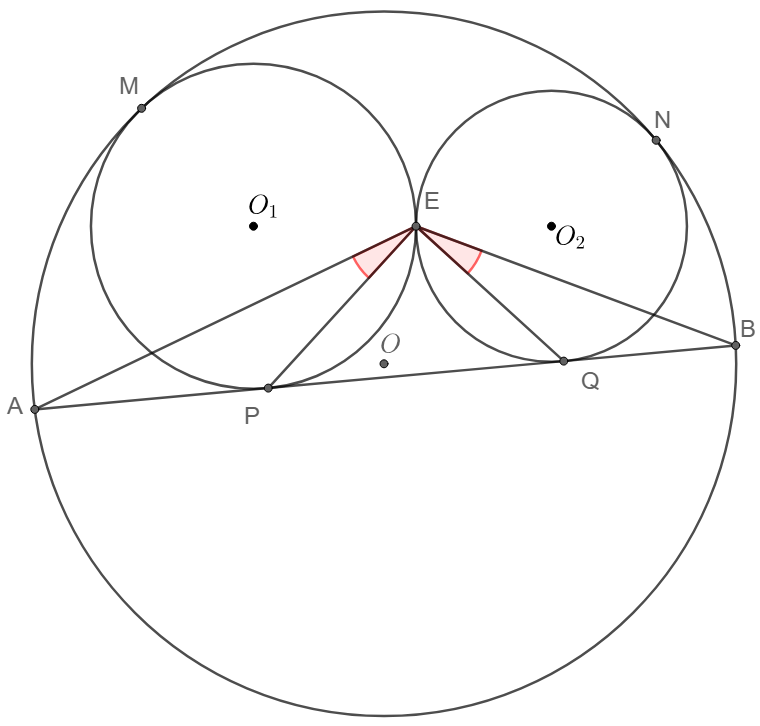
image-20231123031957455

Prove:

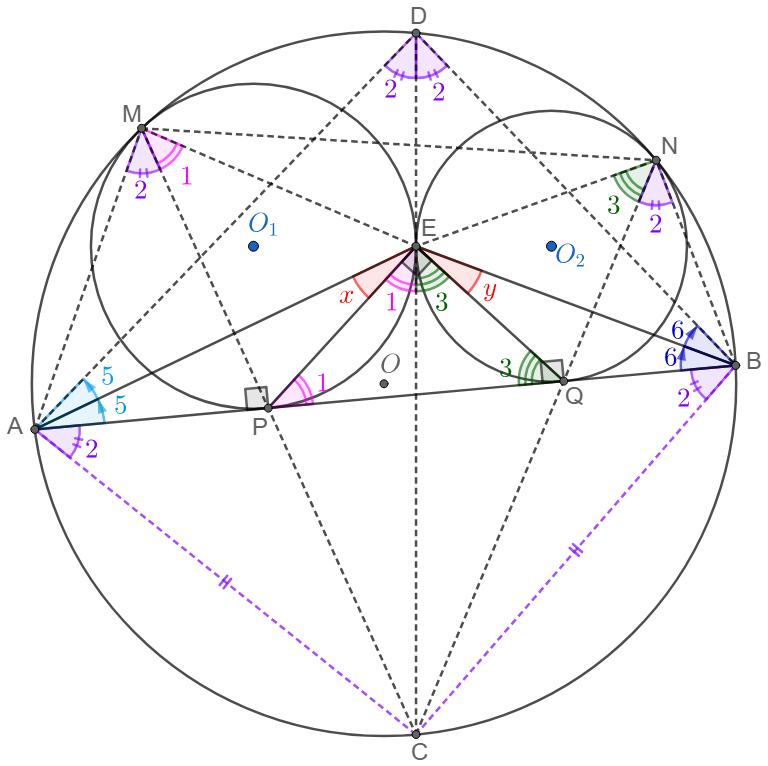
image-20231220175346128 \(\begin{multline}\nonumber \shoveleft \text{Let } M,N \text{ be the tangent points of }\odot{O_1},\odot{O_2} \text{ with }\odot{O}\\ \shoveleft CED \text{ be the tangent line of }\odot{O_!}, \odot{O_2} \text{ and intersect with } \odot{O}\text{ at } C, D\\ \shoveleft \text{The structure of inscribed circles in circular segments has some properties:}\\ \shoveleft AC=BC, E \text{ is the incenter of }\triangle{ABD}: \text{details can be checked at the notes below.}\\ \shoveleft \implies \angle{CAP}=\angle{AMC}=\angle{ADC}=\angle{CDB}=\angle{CNB}=\angle{ABC}=\angle{2}\\ \shoveleft \angle{QPE}=\angle{PEC}=\angle{PME}=\angle{1}, \angle{PQE}=\angle{CEQ}=\angle{ENQ}=\angle{3}\\ \shoveleft \angle{DAE}=\angle{EAP}=\angle{5}, \angle{DBE}=\angle{EBQ}=\angle{6}\\ \shoveleft \angle{1}=\angle{5}+\angle{AEP}, \angle{2}+\angle{5}=\angle{1}+\angle{AEP}\implies \angle{2}=2\angle{AEP}\\ \shoveleft \angle{3}=\angle{6}+\angle{BEQ}, \angle{2}+\angle{6}=\angle{3}+\angle{BEQ}\implies \angle{2}=2 \angle{BEQ}\\ \shoveleft \implies \angle{AEP}=\angle{BEQ}\blacksquare \end{multline}\)

Notes:

  • There are some other properties easy to be proved: $MPQN$ is cyclic, $PE\perp EQ$.
  • Cut-the-knot has some explanations on the topic of circles inscribed in circular segments.
  • Here is the online copy of the best resource on this topic, and here is the local copy of this PDF.

Proof to the properties:

  • $\odot{O_1}$ is tangent to $\odot{O}$ at $M$ and is tangent to secant $AB$ of $\odot{O}$ at $P$, $C$ is the midpoint of arc $\overset{\huge\frown}{AB}$ not containing $M$, then $MPC$ are collinear.

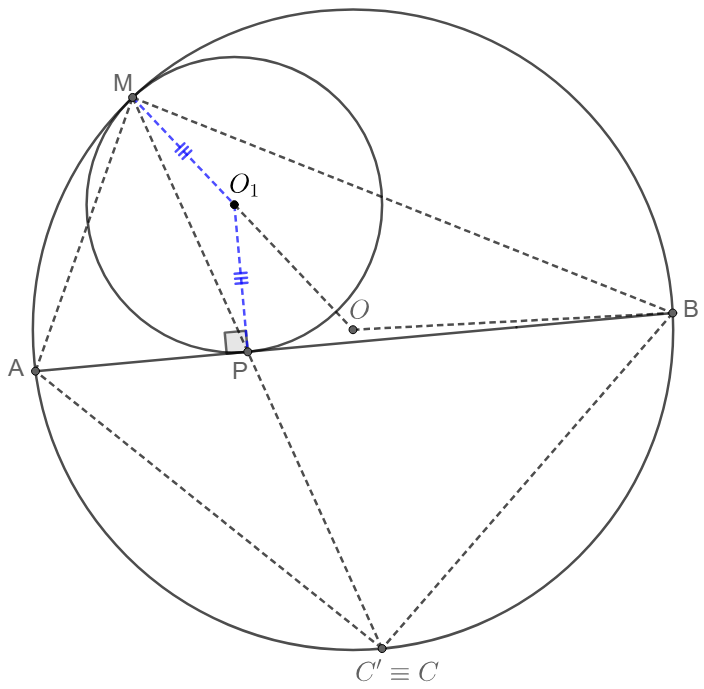image-20231220184528874 \(\begin{multline} \shoveleft \text{Let extended }MP \text{ intersect with }\odot{O} \text{ at }C', \text{ then we prove }C' \equiv C: \\ \shoveleft \angle{BMO}=\dfrac{180^{\circ}-\angle{BOM}}{2}=\dfrac{180^{\circ}-2\angle{BC'M}}{2}=90^{\circ}-\angle{BC'M}\\ \shoveleft \angle{OMP}=\angle{O_1PM}=90^{\circ}-\angle{APM}=90^{\circ}-\angle{BPC'}\\ \shoveleft \implies \angle{BAC'}=\angle{BMC'}=\angle{BMO}+\angle{OMC'}=180^{\circ}-\angle{BC'M}-\angle{BPC'}\\ \shoveleft \implies \angle{BAC'}=\angle{ABC'}\implies AC'=BC' \implies C' \equiv C\blacksquare \end{multline}\)

  • $\odot{O_1}$ is tangent to $\odot{O}$ and is tangent to secant $AB$ of $\odot{O}$, $C$ is the midpoint of arc $\overset{\huge\frown}{AB}$ not containing the tangent point, $CX$ is the tangent segment from $C$ to $\odot{O_1}$, then $CX=CA$.

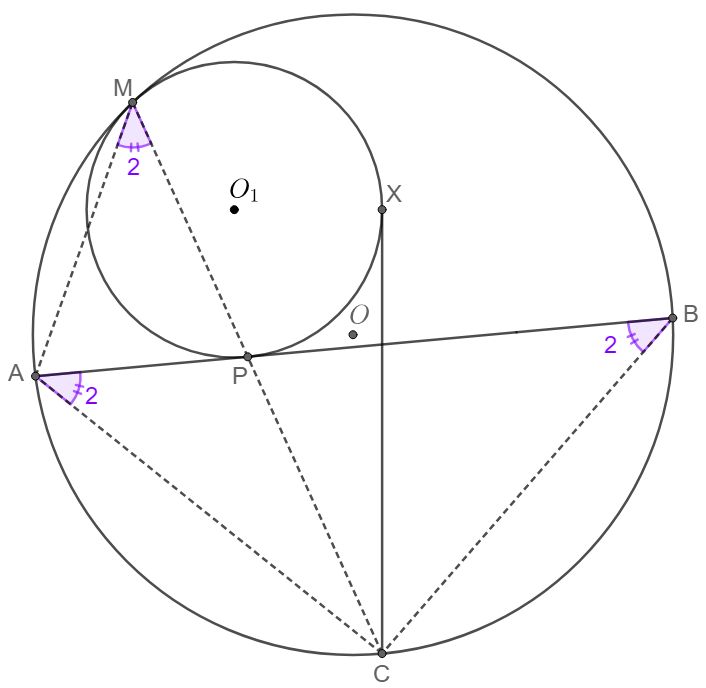image-20231220185152321 \(\begin{multline} \shoveleft AC=BC\implies \angle{CAB}=\angle{CBA}=\angle{CMA}\implies \triangle{ACP}\sim\triangle{MAC}\implies AC^2=CP\cdot CM\\ \shoveleft CX \text{ is tangent to }\odot{O_1} \implies CX^2=CP\cdot CM \text{ by Power of Point} \implies CX=CA\blacksquare \end{multline}\)

  • $\odot{O_1}$ is tangent to $\odot{O}$ at $M$ and is tangent to secant $AB$ of $\odot{O}$ at $P$, $C$ is the midpoint of arc $\overset{\huge\frown}{AB}$ not containing $M$, $\odot{C}$ is the circle passing through $A$ and $B$ with center $C$ and radius $CA$. Let $\odot{C}$ intersect $\odot{O_1}$ at $X$ and $Y$ and intersect $MP$ at $I$, then $MX$ and $MY$ are tangent to $\odot{O_1}$, and $I$ is the incenter of $\triangle{MAB}$.

    image-20231220190211012 $ \begin{multline} \shoveleft \text{We already know }\angle{AMI}=\angle{IMB}
    \shoveleft \angle{CAI}=\angle{CAB}+\angle{BAI}=\angle{CMB}+\angle{BAI}
    \shoveleft \angle{CIA}=\angle{AMC}+\angle{IAM}=\angle{CAB}+\angle{IAM}
    \shoveleft \angle{CAI}=\angle{CIA}\implies \angle{BAI}=\angle{IAM}
    \shoveleft \implies I \text{ is the incenter of }\triangle{IAB}\blacksquare \end{multline} $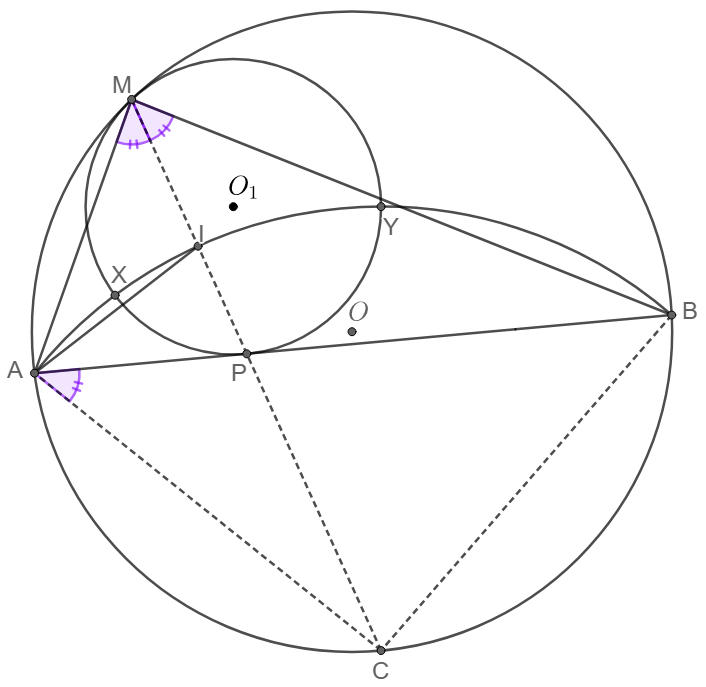

  • Two circles $\odot{O_1}$ and $\odot{O_2}$ are inscribed in secant $AB$ of circle $\odot{O}$ and intersect at point $U, V$. $C$ is the midpoint of arc $\overset{\huge\frown}{AB}$ not containing the tangents of circles. Then $C$ is on the radical axis of $\odot{O_1}$ and $\odot{O_2}$, i.e., $UVC$ are collinear.

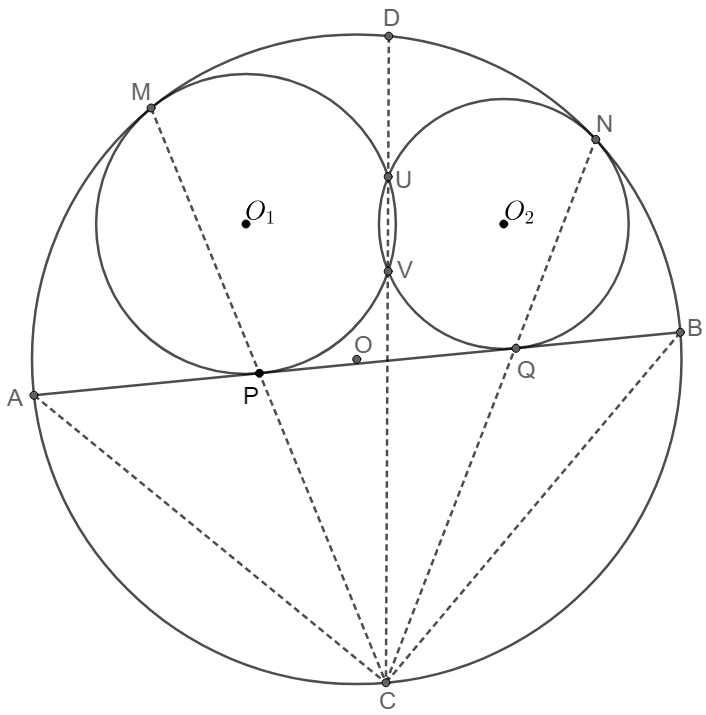
    image-20231220194321362 $ \begin{multline} \shoveleft \text{From above property we know that }C \text{ has the same power of point with respect to }\odot{O_1}\text{ and } \odot{O_2}
    \shoveleft \implies C \text{ is on radical axis of }\odot{O_1} \text{ and }\odot{O_2} \text{ by the definition of radical axis(see note for details)}
    \end{multline} $ Note:

  • Two circles $\odot{O_1}$ and $\odot{O_2}$ are inscribed in secant $AB$ of circle $\odot{O}$ and are tangent to each other externally at point $E$. Let $D$ be the intersect of a common internal tangent to $\odot{O_1}$ and $\odot{O_2}$ with $\odot{O}$ on the same side of $AB$ as the small circles, then $E$ is the incenter of $\triangle{DAB}$.

    image-20231220215229929 $ \begin{multline} \shoveleft \text{When }\odot{O_1} \text{ and }\odot{O_2} \text{ are tangent, their radical axis is the common internal tangent }
    \shoveleft \implies \angle{CAE}=\angle{CAB}+\angle{BAE}=\angle{CDB}+\angle{BAE}
    \shoveleft \angle{CEA} = \angle{ADC} + \angle{EAD}=\angle{CDB}+ \angle{EAD}
    \shoveleft \angle{CAE}=\angle{CEA}\implies \angle{BAE}=\angle{EAD}\implies E \text{ is incenter of }\triangle{DAB} \end{multline} $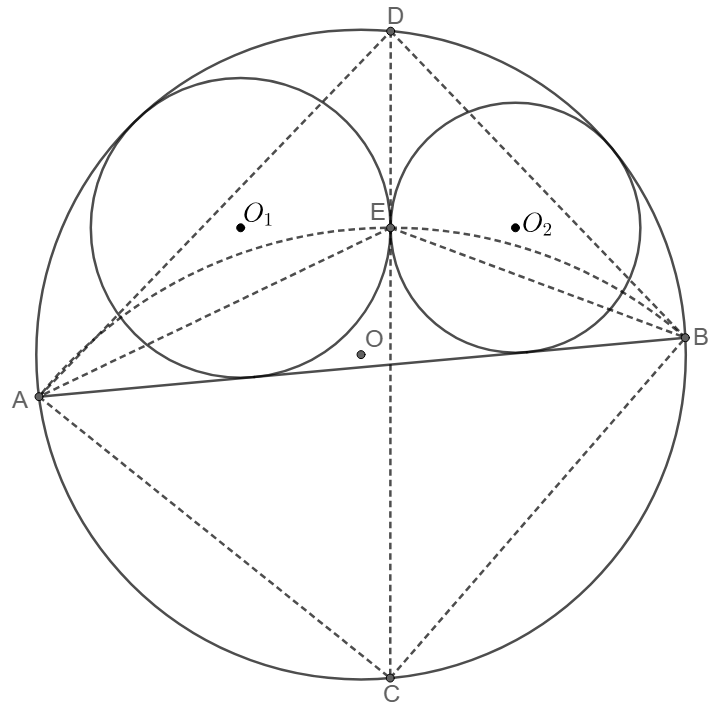

11/30/2023

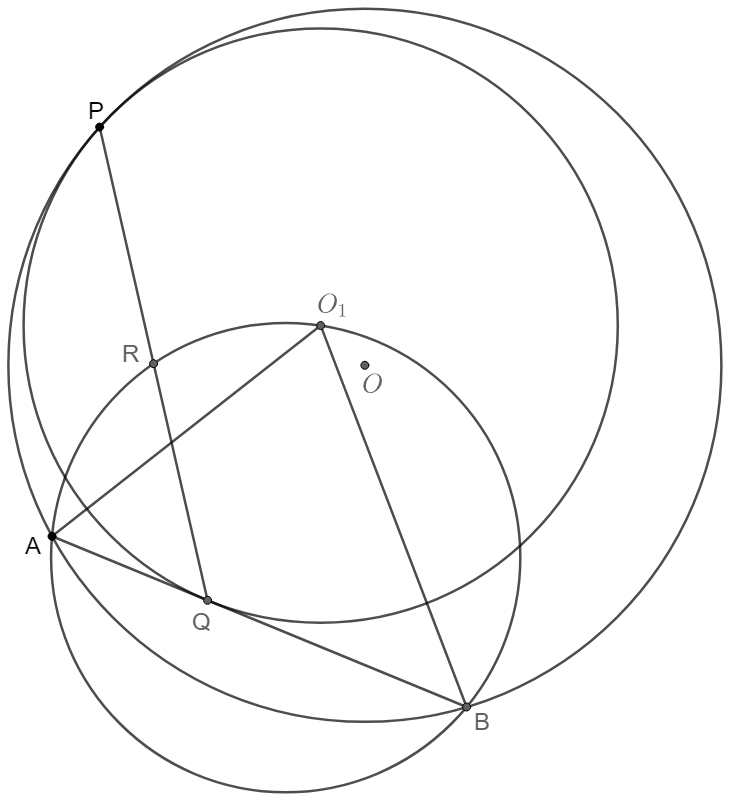
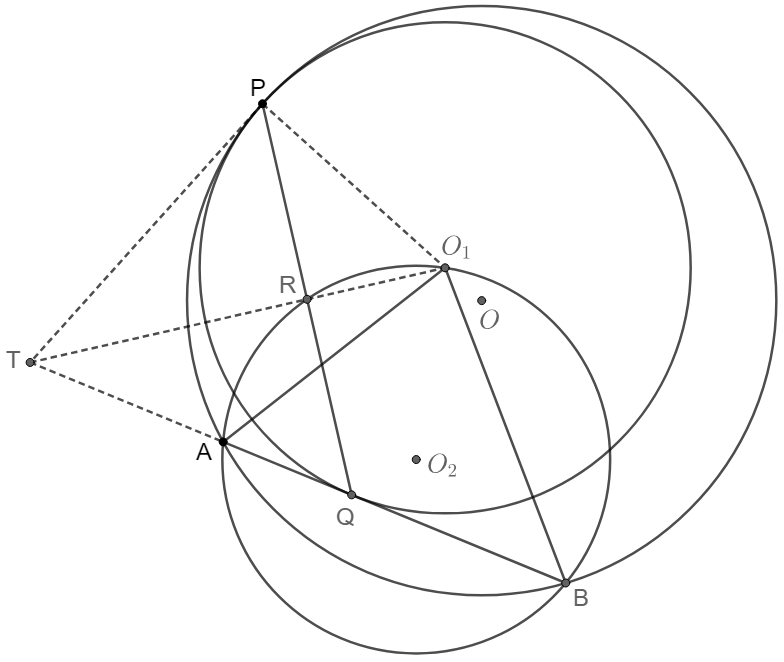
$\odot{O_1}$ is inside $\odot{O}$ and they are tangent at $P$. $AB$ is a secant of $\odot{O}$ and is tangent to $\odot{O_1}$ at $Q$. Prove that the circumcircle of $\triangle{AO_1B}$ bisects $PQ$.

image-20231130193053857

Prove:

image-20231204070321867 \(\begin{multline}\nonumber \shoveleft \text{Let }O_2 \text{ be the center of the circumcircle of }\triangle{AO_1B}\\ \shoveleft \text{Extend }BA \text{ to }T \text{ such that }TP \text{ is tangent to }\odot{O_1} \implies TP\perp PO_1\\ \shoveleft \text{Suppose }R \text{ is the mid point of }PQ \implies TRO_1 \text{ are collinear}, TR \perp PQ\\ \shoveleft \implies TP^2=TR\cdot TO_1, \text{since the Power of Point }T \text{ is constant for each circle:}\\ \shoveleft \text{For }\odot{O}, TP^2=TA \cdot TB \implies TR \cdot TO_1=TA\cdot TB \implies RABO_1 \text{ are cyclic}\\ \shoveleft \implies R \text{ is on }\odot{O_2} \implies R \text{ is the intersect of }\odot{O_2} \text{ and } PQ \implies PR=QR\blacksquare \end{multline}\)

Note: some conclusions can be got from here:

  • The extended $PQ$ and $O_1O_2$ will intersect on $\odot{O_2}$, let it be $C$

  • From previous problem we know that extended $PQ$ and $OO_2$ will intersect on $\odot{O}$, let it be $E$

  • $E$ is the midpoint of $\overset{\huge\frown}{AB}$, and is also the midpoint of $QC$

  • Let $H$ be the orthocenter of $\triangle{AO_1B}$ on $QO_1$, then $C$ is the mirror point of $H$ about $F$

  • Let $H’$ be its mirror point about $AB$, then $H’$ is on $\odot{O_2}$

    image-20231204123628869

    © M∀TH Workout 2020-2021
    Search