10/01/2023
Point $D,E$ are on side $AD, BC$ of $\triangle{ABC}$ such that $\angle{BAC}=\angle{BDE}=90^{\circ}, \angle{DBE}=\angle{CDE}, [ABD]=1, [CDE]=1$, find $[BDE]$.
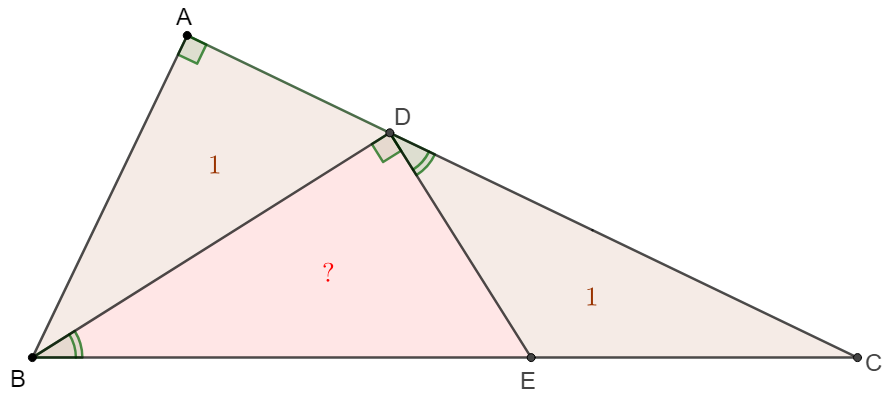
Solve 1:
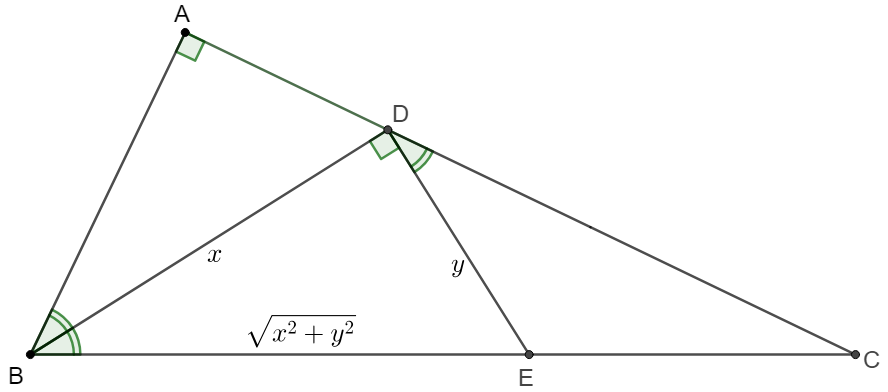 \(\begin{multline}\nonumber
\shoveleft \text{Let }BD=x, DE=y \implies [CBD]=1+\dfrac{xy}{2}\\
\shoveleft \triangle{CDE}\sim \triangle{CBD} \implies \dfrac{[CDE]}{[CBD]}=\dfrac{DE^2}{BD^2}=\dfrac{y^2}{x^2}=\dfrac{1}{1+\dfrac{xy}{2}}\\
\shoveleft \angle{ADB}=90^{\circ}-\angle{CDE}=\angle{ABD}\implies \angle{ABD}=\angle{DBE}\\
\shoveleft \implies \triangle{ABD} \sim \triangle{DBE}\implies \dfrac{[DBE]}{[ABD]}=\dfrac{BE^2}{BD^2}=\dfrac{\dfrac{xy}{2}}{1}=\dfrac{x^2+y^2}{x^2}\\
\shoveleft \implies \dfrac{xy}{2}=\dfrac{4+xy}{2+xy}\implies xy=2\sqrt{2}\implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }BD=x, DE=y \implies [CBD]=1+\dfrac{xy}{2}\\
\shoveleft \triangle{CDE}\sim \triangle{CBD} \implies \dfrac{[CDE]}{[CBD]}=\dfrac{DE^2}{BD^2}=\dfrac{y^2}{x^2}=\dfrac{1}{1+\dfrac{xy}{2}}\\
\shoveleft \angle{ADB}=90^{\circ}-\angle{CDE}=\angle{ABD}\implies \angle{ABD}=\angle{DBE}\\
\shoveleft \implies \triangle{ABD} \sim \triangle{DBE}\implies \dfrac{[DBE]}{[ABD]}=\dfrac{BE^2}{BD^2}=\dfrac{\dfrac{xy}{2}}{1}=\dfrac{x^2+y^2}{x^2}\\
\shoveleft \implies \dfrac{xy}{2}=\dfrac{4+xy}{2+xy}\implies xy=2\sqrt{2}\implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
Solve 2:
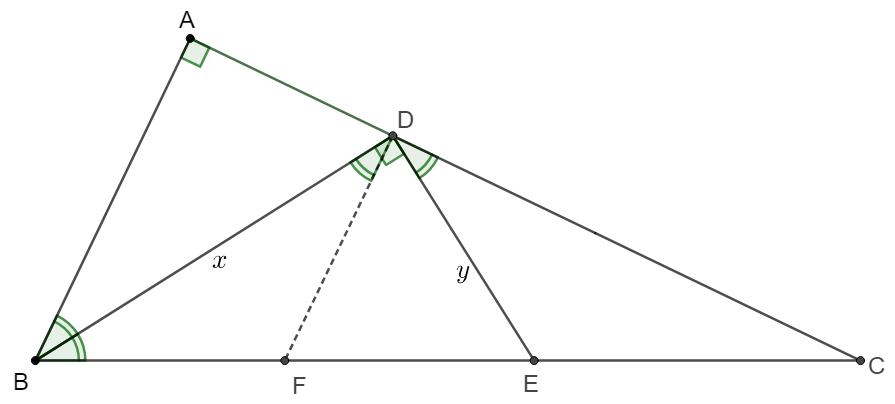 \(\begin{multline}\nonumber
\shoveleft \text{Let }F \text{ be the midpoint of } BE \implies BF=DF=EF\\
\shoveleft \angle{DBF}=\angle{BDF}=\angle{CDE}=\angle{ABD} \implies DF \parallel AB\\
\shoveleft \implies [BFD]=[DEF], \dfrac{[CDF]}{[CAB]}=\dfrac{1+\dfrac{[BDE]}{2}}{2+[BDE]}=\dfrac{1}{2}=\dfrac{CF^2}{BC^2} \\
\shoveleft \implies \dfrac{CF}{BC}=\dfrac{1}{\sqrt{2}} = \dfrac{[CDF]}{[BCD]}=\dfrac{1+\dfrac{[BDE]}{2}}{1+[BDE]}=\dfrac{1}{\sqrt{2}} \implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }F \text{ be the midpoint of } BE \implies BF=DF=EF\\
\shoveleft \angle{DBF}=\angle{BDF}=\angle{CDE}=\angle{ABD} \implies DF \parallel AB\\
\shoveleft \implies [BFD]=[DEF], \dfrac{[CDF]}{[CAB]}=\dfrac{1+\dfrac{[BDE]}{2}}{2+[BDE]}=\dfrac{1}{2}=\dfrac{CF^2}{BC^2} \\
\shoveleft \implies \dfrac{CF}{BC}=\dfrac{1}{\sqrt{2}} = \dfrac{[CDF]}{[BCD]}=\dfrac{1+\dfrac{[BDE]}{2}}{1+[BDE]}=\dfrac{1}{\sqrt{2}} \implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
Solve 3:
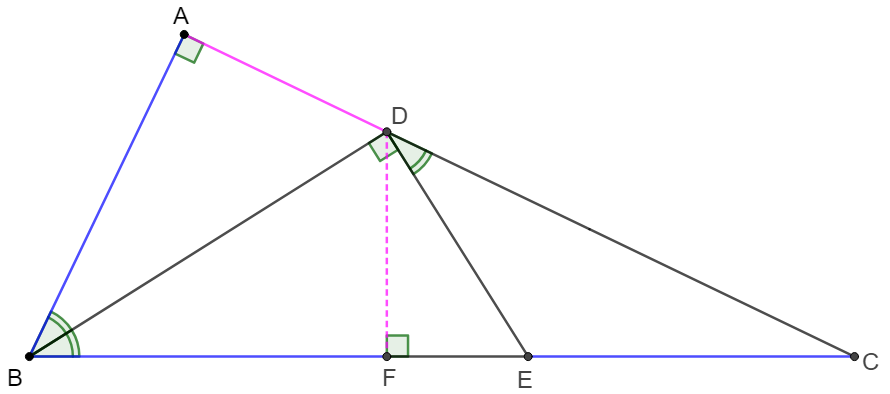 \(\begin{multline}\nonumber
\shoveleft \text{Make }DF\perp BC \text{ at } F \implies \\
\shoveleft \angle{CDE}=90^{\circ}-\angle{ADB}=\angle{ABD}=\angle{DBE}=\angle{EDF}\\
\shoveleft \implies BD \text{ bisects } \angle{ABC}, DE \text{ bisects } \angle{CDF}\\
\shoveleft \implies AD=DF, [BDF]=[BAD]=1, \dfrac{BC}{AB}=\dfrac{CD}{DA}=\dfrac{CD}{DF}=\dfrac{CE}{EF}\\
\shoveleft \implies \dfrac{[BCD]}{[BAD]}=\dfrac{[CDE]}{[DEF]}\implies \dfrac{1+[BDE]}{1}=\dfrac{[1]}{[BDE]-1}\\
\shoveleft \implies [BDE]^2=2\implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Make }DF\perp BC \text{ at } F \implies \\
\shoveleft \angle{CDE}=90^{\circ}-\angle{ADB}=\angle{ABD}=\angle{DBE}=\angle{EDF}\\
\shoveleft \implies BD \text{ bisects } \angle{ABC}, DE \text{ bisects } \angle{CDF}\\
\shoveleft \implies AD=DF, [BDF]=[BAD]=1, \dfrac{BC}{AB}=\dfrac{CD}{DA}=\dfrac{CD}{DF}=\dfrac{CE}{EF}\\
\shoveleft \implies \dfrac{[BCD]}{[BAD]}=\dfrac{[CDE]}{[DEF]}\implies \dfrac{1+[BDE]}{1}=\dfrac{[1]}{[BDE]-1}\\
\shoveleft \implies [BDE]^2=2\implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}}
\end{multline}\)
10/02/2023
$D$ is a point on lateral side $CD$ of trapezoid $ABCD$ such that $\dfrac{CE}{DE}=\dfrac{3}{1}, [ADE]=9, [BCE]=21$, find $[ABE]$
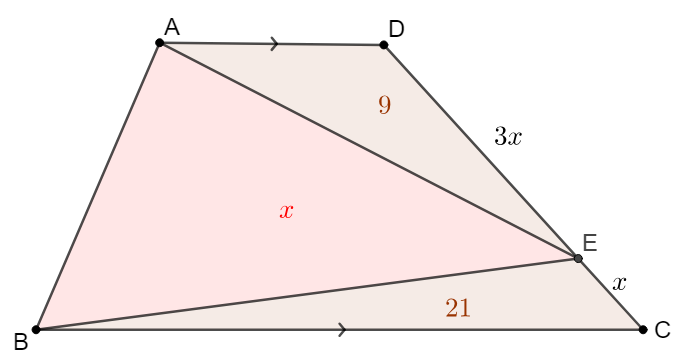
Solve:
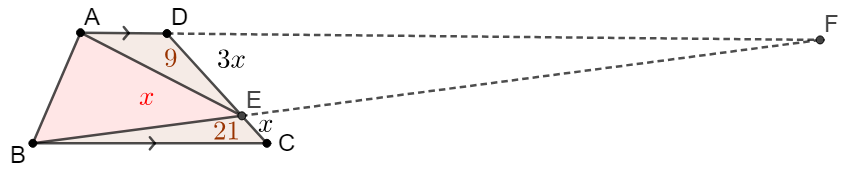 \(\begin{multline}\nonumber
\shoveleft \text{Let extended } AD, BE \text{ intersect at }F.\\
\shoveleft \triangle{DEF} \sim \triangle{CEB} \implies \dfrac{[DEF]}{[CEB]}=\dfrac{DE^2}{CD^2}=9\\
\shoveleft \implies [DEF]=21 \times 9=189\implies [AEF]=198\\
\shoveleft \dfrac{[ABF]}{[AEF]}=\dfrac{CD}{DE}=\dfrac{4}{3}\implies [ABF]=198 \times \dfrac{4}{3}=264\\
\shoveleft \implies [ABE]=[ABF]-[AEF]=264-198=\bbox[5px, border: 1px solid black]{66}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let extended } AD, BE \text{ intersect at }F.\\
\shoveleft \triangle{DEF} \sim \triangle{CEB} \implies \dfrac{[DEF]}{[CEB]}=\dfrac{DE^2}{CD^2}=9\\
\shoveleft \implies [DEF]=21 \times 9=189\implies [AEF]=198\\
\shoveleft \dfrac{[ABF]}{[AEF]}=\dfrac{CD}{DE}=\dfrac{4}{3}\implies [ABF]=198 \times \dfrac{4}{3}=264\\
\shoveleft \implies [ABE]=[ABF]-[AEF]=264-198=\bbox[5px, border: 1px solid black]{66}
\end{multline}\)
10/03/2023
Trapezoid $ABCD$ has $\angle{ABC}=\angle{BAD}=90^{\circ}, BC=12, AD=14$. Point $E, F$ are on side $AB, CD$ respectively. Point $C, E$ is tangent to circle. $D$ is on the circle. $EF \perp CD$ at $F$. Find $EF$
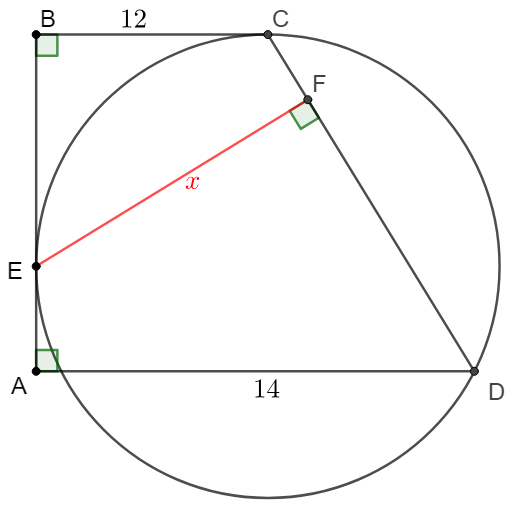
Solve:
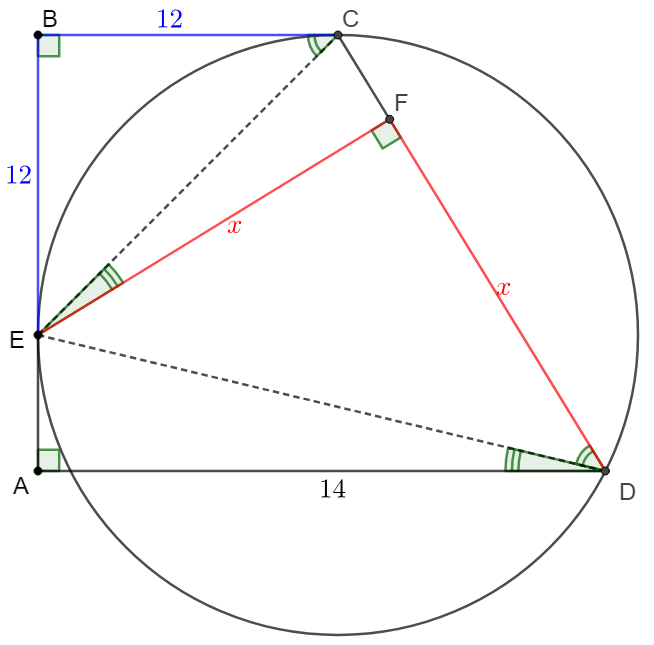 \(\begin{multline}\nonumber
\shoveleft \text{Easy to see that } BE=BC=12, EF=FD=x\\
\shoveleft \angle{BCE}=\angle{BEC}=\angle{FED}=\angle{FDE}=45^{\circ}\\
\shoveleft \implies \triangle{BEC}\sim\triangle{FED} \implies \dfrac{12}{x}=\dfrac{EC}{ED}\\
\shoveleft \angle{AED}=\angle{ECD}\implies \angle{EDA}=\angle{CEF}\\
\shoveleft \implies \triangle{CEF}\sim\triangle{EDA} \implies \dfrac{EC}{ED}=\dfrac{x}{14}\\
\shoveleft \implies \dfrac{12}{x}=\dfrac{x}{14} \implies x^2=12 \times 14 \implies x=\bbox[5px, border: 1px solid black]{2\sqrt{42}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Easy to see that } BE=BC=12, EF=FD=x\\
\shoveleft \angle{BCE}=\angle{BEC}=\angle{FED}=\angle{FDE}=45^{\circ}\\
\shoveleft \implies \triangle{BEC}\sim\triangle{FED} \implies \dfrac{12}{x}=\dfrac{EC}{ED}\\
\shoveleft \angle{AED}=\angle{ECD}\implies \angle{EDA}=\angle{CEF}\\
\shoveleft \implies \triangle{CEF}\sim\triangle{EDA} \implies \dfrac{EC}{ED}=\dfrac{x}{14}\\
\shoveleft \implies \dfrac{12}{x}=\dfrac{x}{14} \implies x^2=12 \times 14 \implies x=\bbox[5px, border: 1px solid black]{2\sqrt{42}}
\end{multline}\)
10/04/2023
$D$ is a point inside $\triangle{ABC}$ such that $\angle{BAD}=20^{\circ}, \angle{DAC}=40^{\circ}, \angle{DBC}=\angle{DCB}=10^{\circ}$, find $\angle{ABD}$
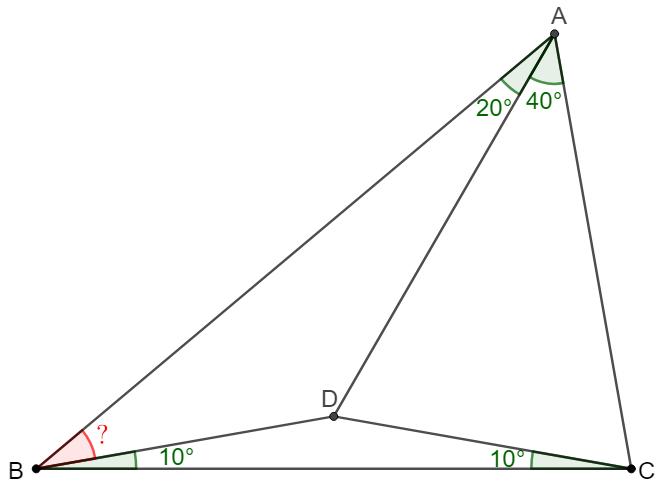
Solve:
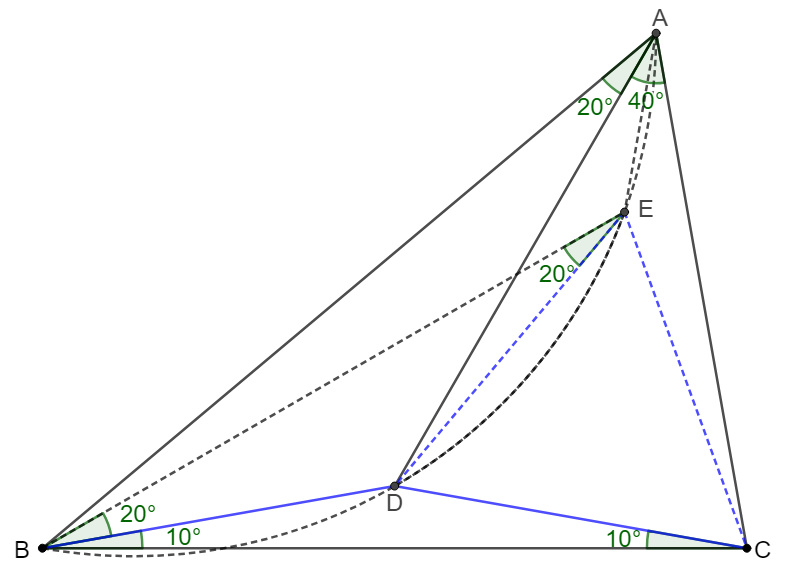 \(\begin{multline}\nonumber
\shoveleft \text{Let }E \text{ be a point on the circumcircle of } \triangle{ABD} \text{ such that } BD=DE=CD\\
\shoveleft \implies \angle{BAD}=\angle{BED}=\angle{DBE}=\angle{DAE}=20^{\circ}=\angle{CAE}\\
\shoveleft \implies \angle{CDE}=360^{\circ}-\angle{BDE}-\angle{BDC}=360^{\circ}-140^{\circ}-160^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{CDE} \text{ is equilateral} \implies CE=DE \implies \triangle{DAE}\cong\triangle{CAE}\\
\shoveleft \implies AC=AD\implies \angle{ACD}=\angle{ADC}=70^{\circ} \implies \angle{ABD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }E \text{ be a point on the circumcircle of } \triangle{ABD} \text{ such that } BD=DE=CD\\
\shoveleft \implies \angle{BAD}=\angle{BED}=\angle{DBE}=\angle{DAE}=20^{\circ}=\angle{CAE}\\
\shoveleft \implies \angle{CDE}=360^{\circ}-\angle{BDE}-\angle{BDC}=360^{\circ}-140^{\circ}-160^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{CDE} \text{ is equilateral} \implies CE=DE \implies \triangle{DAE}\cong\triangle{CAE}\\
\shoveleft \implies AC=AD\implies \angle{ACD}=\angle{ADC}=70^{\circ} \implies \angle{ABD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
10/05/2023
$\triangle{ABC}, \triangle{BEF}$ are equilateral triangles. Extend $CF$ and intersect $AE$ at $D$ . Find $\angle{ADC}$.
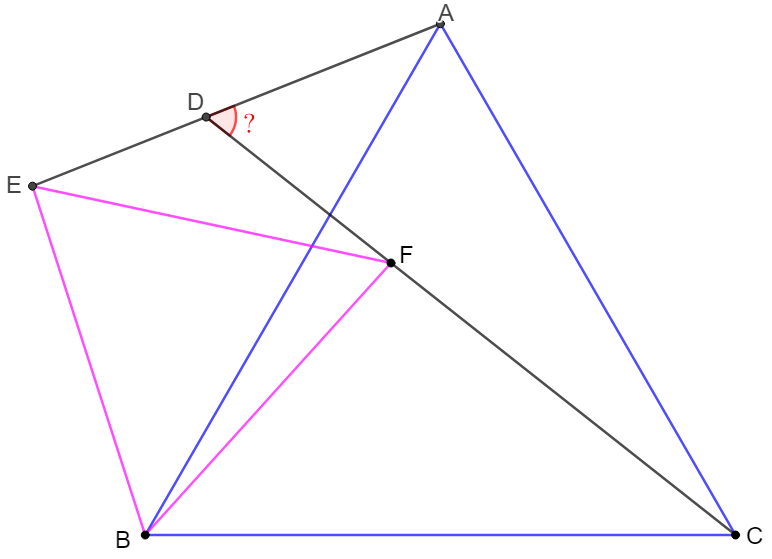
Solve:
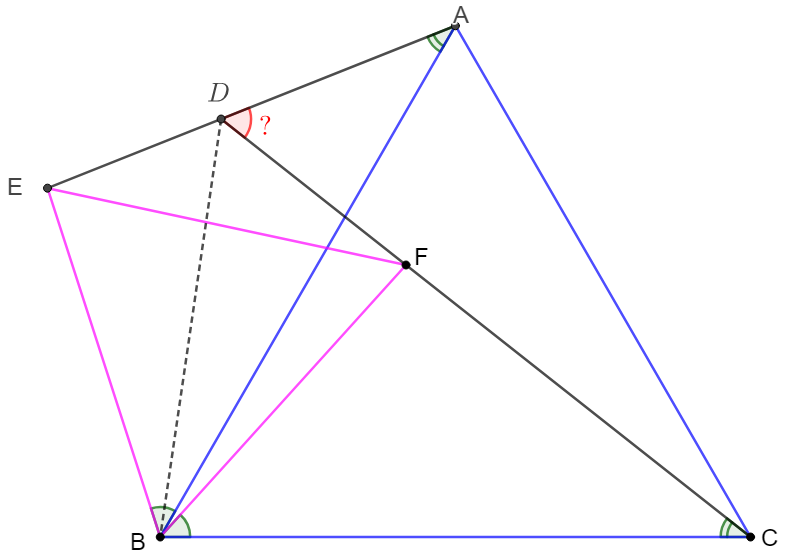 \(\begin{multline}\nonumber
\shoveleft \angle{EBF}=\angle{ABC}=60^{\circ} \implies \angle{EBA}=\angle{FBC}, EB=FB,AB=CB\\
\shoveleft \implies \triangle{EBA}\cong\triangle{FBC}\implies \angle{EAB}=\angle{FCB}\implies ADBC \text{ is cyclic}\\
\shoveleft \implies \angle{ADC}=\angle{ABC}=\bbox[5px, border: 1px solid black]{60^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \angle{EBF}=\angle{ABC}=60^{\circ} \implies \angle{EBA}=\angle{FBC}, EB=FB,AB=CB\\
\shoveleft \implies \triangle{EBA}\cong\triangle{FBC}\implies \angle{EAB}=\angle{FCB}\implies ADBC \text{ is cyclic}\\
\shoveleft \implies \angle{ADC}=\angle{ABC}=\bbox[5px, border: 1px solid black]{60^{\circ}}
\end{multline}\)
10/06/2023
$D$ is a point on side $BC$ of $\triangle{ABC}$ and $\angle{ABC}=30^{\circ}, \angle{ACB}=100^{\circ}, AD=BC$. Find $\angle{ADC}$.
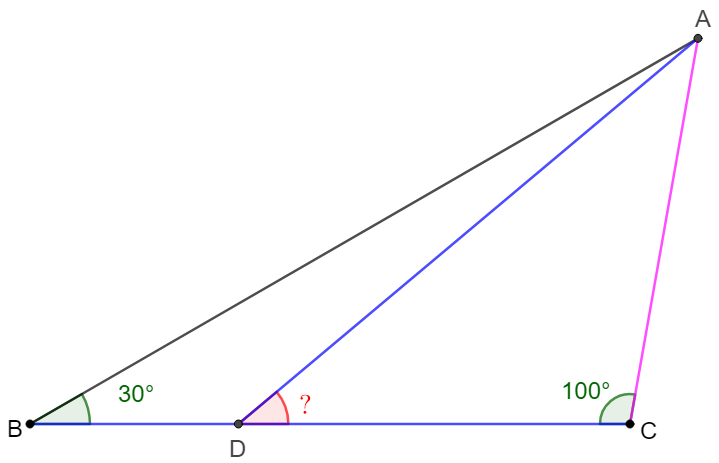
Solve:
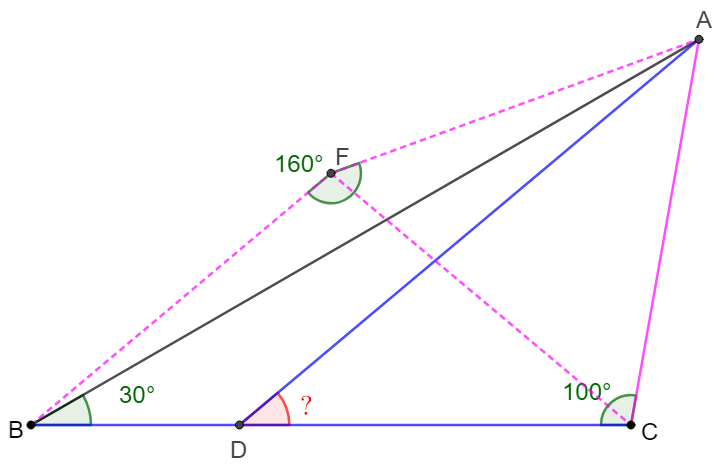 \(\begin{multline}\nonumber
\shoveleft \text{Let } F \text{ be the circumcenter of } \triangle{ABC} \implies AF=BF=CF, \\
\shoveleft \angle{AFC}=2\angle{ABC}=60^{\circ}, \angle{AFB}=360^{\circ}-2\times \angle{ACB}=160^{\circ}\\
\shoveleft \implies \angle{BFC}=100^{\circ}=\angle{ACB},\triangle{AFC} \text{ is equilateral} \\
\shoveleft \implies CF=AC\implies \triangle{BFC} \cong\triangle{ACD} \text{ (SSA on obtuse triangles)}\\
\shoveleft \implies \angle{ADC}=\angle{FBC}=\angle{FCB=}\dfrac{180^{\circ}-\angle{BFC}}{2}=\bbox[5px, border: 1px solid black]{40^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let } F \text{ be the circumcenter of } \triangle{ABC} \implies AF=BF=CF, \\
\shoveleft \angle{AFC}=2\angle{ABC}=60^{\circ}, \angle{AFB}=360^{\circ}-2\times \angle{ACB}=160^{\circ}\\
\shoveleft \implies \angle{BFC}=100^{\circ}=\angle{ACB},\triangle{AFC} \text{ is equilateral} \\
\shoveleft \implies CF=AC\implies \triangle{BFC} \cong\triangle{ACD} \text{ (SSA on obtuse triangles)}\\
\shoveleft \implies \angle{ADC}=\angle{FBC}=\angle{FCB=}\dfrac{180^{\circ}-\angle{BFC}}{2}=\bbox[5px, border: 1px solid black]{40^{\circ}}
\end{multline}\)
10/19/2023
$D$ is a point inside $\triangle{ABC}$ and $M, N$ are intersection points of extended $BD, CD$ on side $AC, AB$. $AM:MC=3:1, AN:NB=3:2, [ABC]=6$, find $[BCD]$.
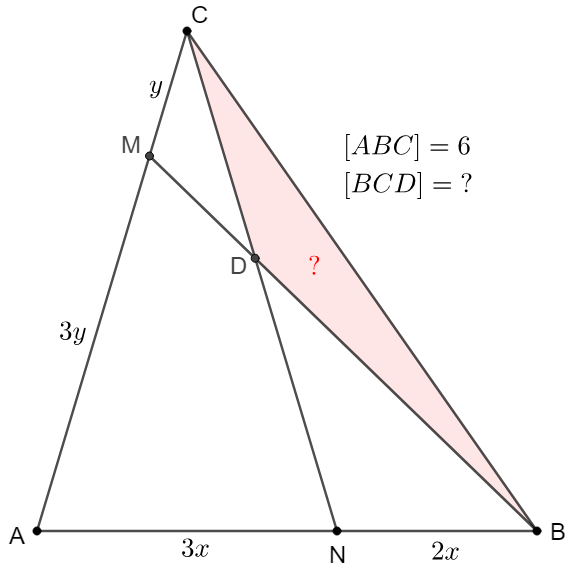
Solve: \(\begin{multline}\nonumber \shoveleft \text{Apply the Extended Crossed Ladders Theorem:} \\ \shoveleft \dfrac{1}{[BCM]}+\dfrac{1}{[BCN]}=\dfrac{1}{[BCD]} + \dfrac{1}{[ABC]}\\ \shoveleft \text{And we know } [BCM]=\dfrac{[ABC]}{4},[BCN]=\dfrac{2[ABC]}{5}\\ \shoveleft \implies \dfrac{1}{[BCD]}=\dfrac{4}{[ABC]}+\dfrac{5}{2[ABC]}-\dfrac{1}{[ABC]}\\ \shoveleft \implies \dfrac{1}{[BCD]}=\dfrac{11}{2[ABC]}=\dfrac{11}{12} \implies [BCD]=\bbox[5px, border: 1px solid black]{\dfrac{12}{11}} \end{multline}\) Note: Extended Cross Ladders Theorem
10/20/2023
$O$ is a point in $\triangle{ABC}$ and $\angle{A}=60^{\circ}, \angle{OBC}=\angle{OCB}=30^{\circ}$, $D, E$ are intersection points of extended $CO, BO$ and $AB, AC$. $G$ is on $BC$ such that $OG \perp BC$. Show that $2 OG=OD+OE$.
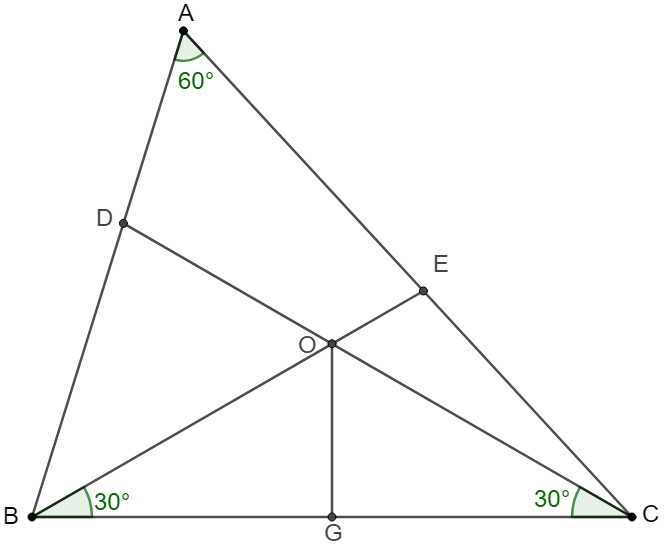
Prove 1:
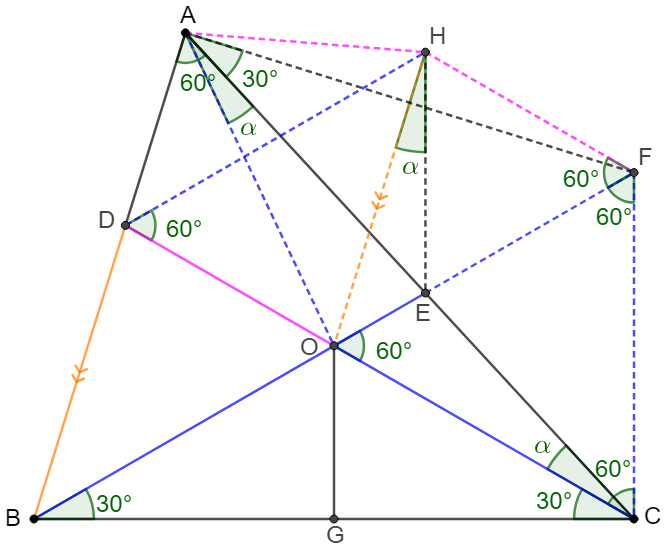 \(\begin{multline}\nonumber
\shoveleft \text{Extend }BE \text{ to } F \text{ such that } CF \perp BC, \text{ easy to see that}\\
\shoveleft \angle{COF}=60^{\circ}, BO=CO \implies \triangle{CFO} \text{ is equilateral}\\
\shoveleft \implies CF=CO=BO=FO=2OG,\angle{FCO}=\angle{CFO}=60^{\circ}\\
\shoveleft \text{Connect }AO, AF. \angle{BAC}=\angle{BFC}=60^{\circ}\implies ABCF \text{ is cyclic}\\
\shoveleft \implies \angle{BAF}=\angle{BCF}=90^{\circ}, \angle{CAF}=\angle{CBF}=30^{\circ}\\
\shoveleft \implies BO=FO=AO=CO \implies \angle{OAC}=\angle{OCA}\\
\shoveleft \text{Make }FH\parallel OD, DH \parallel FO \implies DHFO \text{ is parallelogram}\\
\shoveleft \implies DO=HF, DH=OF,\angle{HFO}=\angle{HDO}=\angle{DOB}=60^{\circ}\\
\shoveleft \implies \triangle{DOB}\cong\triangle{HFO}\implies \angle{HOF}=\angle{DBO} \implies HO \parallel AB \\
\shoveleft \implies \angle{HOF}=\angle{DBO}=\angle{ADH}=\angle{BAO}=\angle{DHO}\\
\shoveleft \implies ADOH \text{ is cyclic} \implies \angle{HAO}=\angle{HDO}=\angle{DOB}=60^{\circ}\\
\shoveleft \implies \angle{HAE}=60^{\circ}-\angle{OAE}=\angle{BAO}=\angle{ABO}=\angle{HOE} \\
\shoveleft \implies AOEH \text{ is cyclic}\implies \angle{HEF}=\angle{HAO}\implies \triangle{HEF} \text{ is equilateral}\\
\shoveleft \implies EF=HF=OD\implies 2OG=OF=OE+OD\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Extend }BE \text{ to } F \text{ such that } CF \perp BC, \text{ easy to see that}\\
\shoveleft \angle{COF}=60^{\circ}, BO=CO \implies \triangle{CFO} \text{ is equilateral}\\
\shoveleft \implies CF=CO=BO=FO=2OG,\angle{FCO}=\angle{CFO}=60^{\circ}\\
\shoveleft \text{Connect }AO, AF. \angle{BAC}=\angle{BFC}=60^{\circ}\implies ABCF \text{ is cyclic}\\
\shoveleft \implies \angle{BAF}=\angle{BCF}=90^{\circ}, \angle{CAF}=\angle{CBF}=30^{\circ}\\
\shoveleft \implies BO=FO=AO=CO \implies \angle{OAC}=\angle{OCA}\\
\shoveleft \text{Make }FH\parallel OD, DH \parallel FO \implies DHFO \text{ is parallelogram}\\
\shoveleft \implies DO=HF, DH=OF,\angle{HFO}=\angle{HDO}=\angle{DOB}=60^{\circ}\\
\shoveleft \implies \triangle{DOB}\cong\triangle{HFO}\implies \angle{HOF}=\angle{DBO} \implies HO \parallel AB \\
\shoveleft \implies \angle{HOF}=\angle{DBO}=\angle{ADH}=\angle{BAO}=\angle{DHO}\\
\shoveleft \implies ADOH \text{ is cyclic} \implies \angle{HAO}=\angle{HDO}=\angle{DOB}=60^{\circ}\\
\shoveleft \implies \angle{HAE}=60^{\circ}-\angle{OAE}=\angle{BAO}=\angle{ABO}=\angle{HOE} \\
\shoveleft \implies AOEH \text{ is cyclic}\implies \angle{HEF}=\angle{HAO}\implies \triangle{HEF} \text{ is equilateral}\\
\shoveleft \implies EF=HF=OD\implies 2OG=OF=OE+OD\blacksquare
\end{multline}\)
Prove 2:
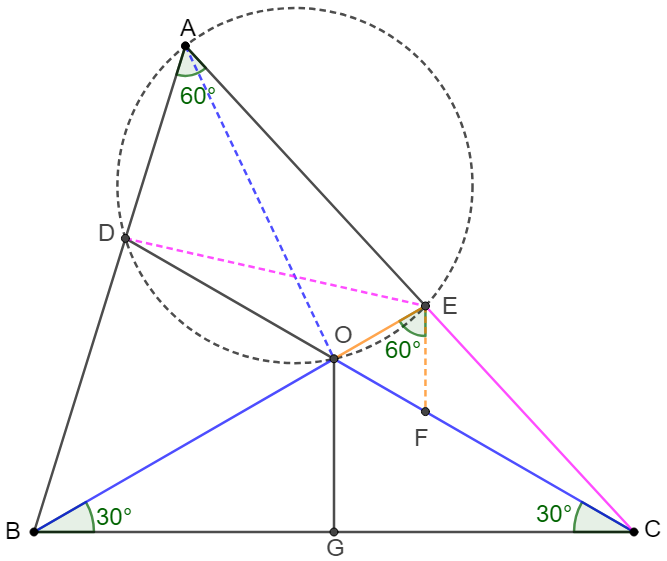 \(\begin{multline}\nonumber
\shoveleft BO=CO, \angle{BOC}=120^{\circ}=2\angle{BAC}\\
\shoveleft \implies O \text{ is circumcenter of }\triangle{ABC}\\
\shoveleft \implies AO=BO=CO\implies \angle{OAC}=\angle{OCA}\\
\shoveleft \angle{BAC}=\angle{COE}=60^{\circ}\implies ADOE \text{ is cyclic}\\
\shoveleft \implies \angle{OAC}=\angle{ODE} \implies \angle{ODE}=\angle{OCA}\\
\shoveleft \implies DE=CE\\
\shoveleft \text{Make }F \text{ on } OC \text{ such that }OE=OF\\
\shoveleft \implies OEF \text{ is equilateral}\implies OE=EF=OF\\
\shoveleft \angle{DOE}=\angle{EFC}=120^{\circ}\implies \triangle{DOE}\cong\triangle{CEF}\\
\shoveleft \implies OD=CF\implies 2OG=OC=OE+OD\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft BO=CO, \angle{BOC}=120^{\circ}=2\angle{BAC}\\
\shoveleft \implies O \text{ is circumcenter of }\triangle{ABC}\\
\shoveleft \implies AO=BO=CO\implies \angle{OAC}=\angle{OCA}\\
\shoveleft \angle{BAC}=\angle{COE}=60^{\circ}\implies ADOE \text{ is cyclic}\\
\shoveleft \implies \angle{OAC}=\angle{ODE} \implies \angle{ODE}=\angle{OCA}\\
\shoveleft \implies DE=CE\\
\shoveleft \text{Make }F \text{ on } OC \text{ such that }OE=OF\\
\shoveleft \implies OEF \text{ is equilateral}\implies OE=EF=OF\\
\shoveleft \angle{DOE}=\angle{EFC}=120^{\circ}\implies \triangle{DOE}\cong\triangle{CEF}\\
\shoveleft \implies OD=CF\implies 2OG=OC=OE+OD\blacksquare
\end{multline}\)
Prove 3:
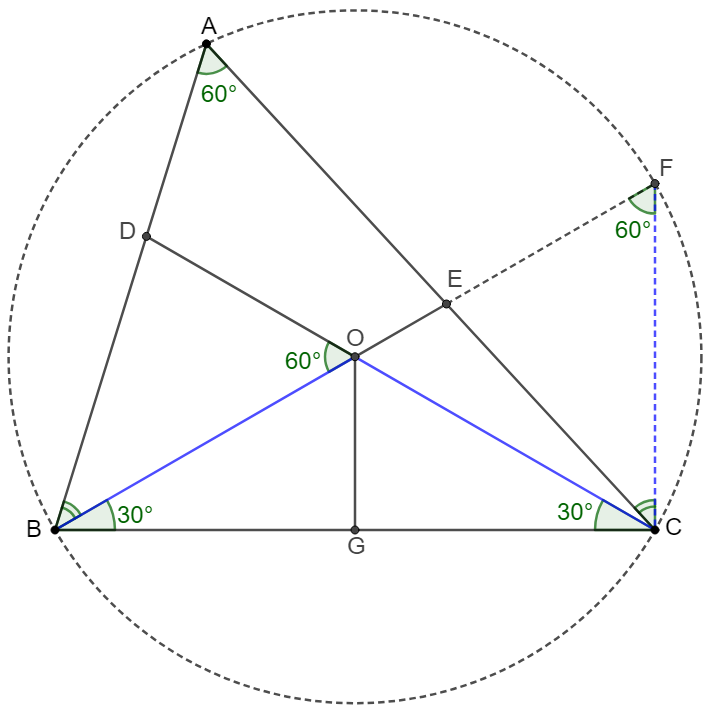 \(\begin{multline}\nonumber
\shoveleft BO=CO, \angle{BOC}=120^{\circ}=2\angle{BAC}\implies O \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \text{Extend } OE \text{ to } F \text{ such that } F \text{ is on the circumcircle of } \triangle{ABC} \implies \angle{ABF}=\angle{ACF} \\
\shoveleft \angle{BFC}=\angle{BAC}=60^{\circ}=\angle{BOD} \implies \triangle{OCF}\text{ is equilateral} \implies CF=OC=BO\\
\shoveleft \implies \triangle{BDO}\cong\triangle{CEF}\implies OD=EF \implies 2OG=OF=OE+OD\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft BO=CO, \angle{BOC}=120^{\circ}=2\angle{BAC}\implies O \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \text{Extend } OE \text{ to } F \text{ such that } F \text{ is on the circumcircle of } \triangle{ABC} \implies \angle{ABF}=\angle{ACF} \\
\shoveleft \angle{BFC}=\angle{BAC}=60^{\circ}=\angle{BOD} \implies \triangle{OCF}\text{ is equilateral} \implies CF=OC=BO\\
\shoveleft \implies \triangle{BDO}\cong\triangle{CEF}\implies OD=EF \implies 2OG=OF=OE+OD\blacksquare
\end{multline}\)
10/21/2023
$E$ is midpoint of side $AD$ of square $ABCD$, $F$ is the intersection of $AC$ and $BE$. Find $\dfrac{[BCF]}{[ABCD]}$.
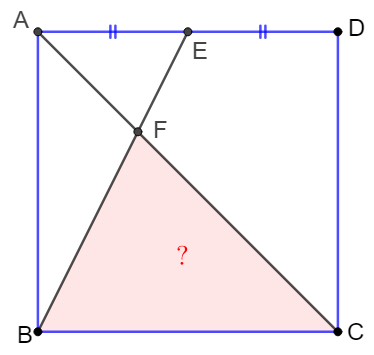
Solve:
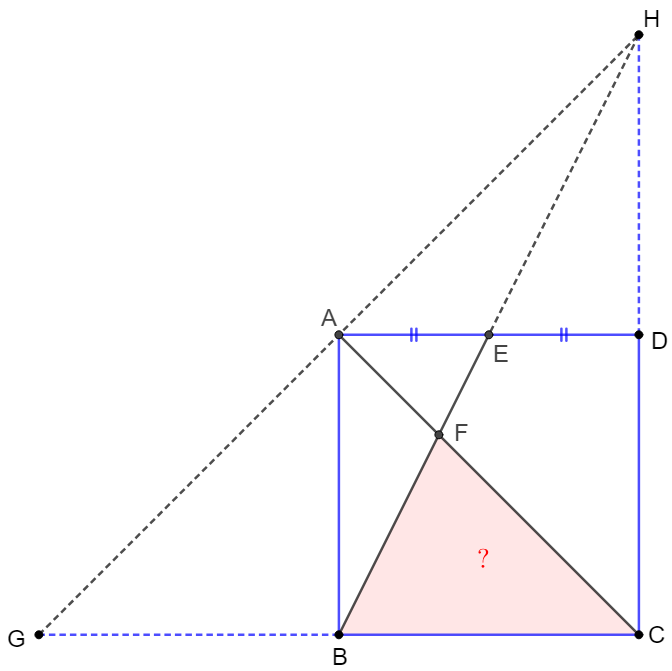 \(\begin{multline}\nonumber
\shoveleft \text{Extend }CB, CD \text{ such that } GB=BC=HD=CD, \text{ easy to see } GAH, BEH \text{ is collinear}.\\
\shoveleft \text{Apply Extended Crossed Ladder Theorem} \implies \dfrac{1}{[ACH]}+\dfrac{1}{[BCH]}=\dfrac{1}{[FCH]}+\dfrac{1}{[GCH]}\\
\shoveleft 2[ACH]=2[BCH]=[GCH] \implies [FCH]=\dfrac{[GCH]}{3}=\dfrac{2[ABCD]}{3}\\
\shoveleft \implies[BCF]=[BCH]-[FCH]=[ABCD]-[FCH]=\dfrac{[ABCD]}{3}\implies \dfrac{[BCF]}{[ABCD]}=\bbox[5px, border: 1px solid black]{\dfrac{1}{3}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Extend }CB, CD \text{ such that } GB=BC=HD=CD, \text{ easy to see } GAH, BEH \text{ is collinear}.\\
\shoveleft \text{Apply Extended Crossed Ladder Theorem} \implies \dfrac{1}{[ACH]}+\dfrac{1}{[BCH]}=\dfrac{1}{[FCH]}+\dfrac{1}{[GCH]}\\
\shoveleft 2[ACH]=2[BCH]=[GCH] \implies [FCH]=\dfrac{[GCH]}{3}=\dfrac{2[ABCD]}{3}\\
\shoveleft \implies[BCF]=[BCH]-[FCH]=[ABCD]-[FCH]=\dfrac{[ABCD]}{3}\implies \dfrac{[BCF]}{[ABCD]}=\bbox[5px, border: 1px solid black]{\dfrac{1}{3}}
\end{multline}\)
10/25/2023
$ABCD$ is a parallelogram and $O$ is the intersection of its diagonals. Point $E$ is on side $CD$ such that $\dfrac{CE}{DE}=\dfrac{1}{3}$. $F$ is on side $AB$. CF intersects with $AE, AD$ at $H, J$ such that $CH=HJ=JF$. $[ABCD]=240$, find $[GHJO]$.
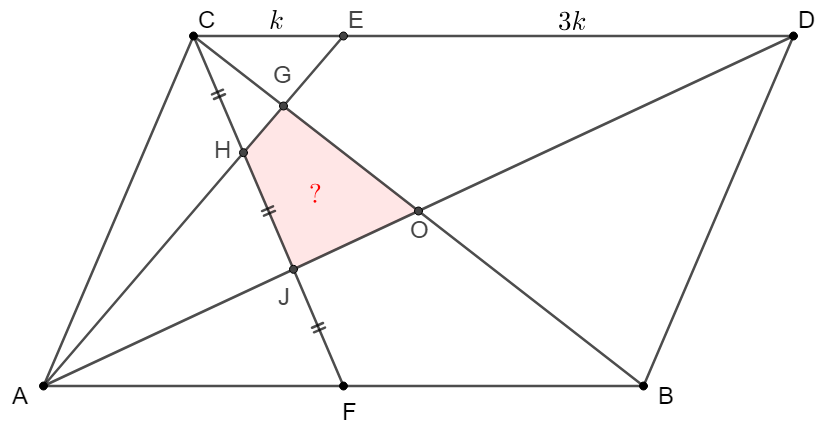
Solve:
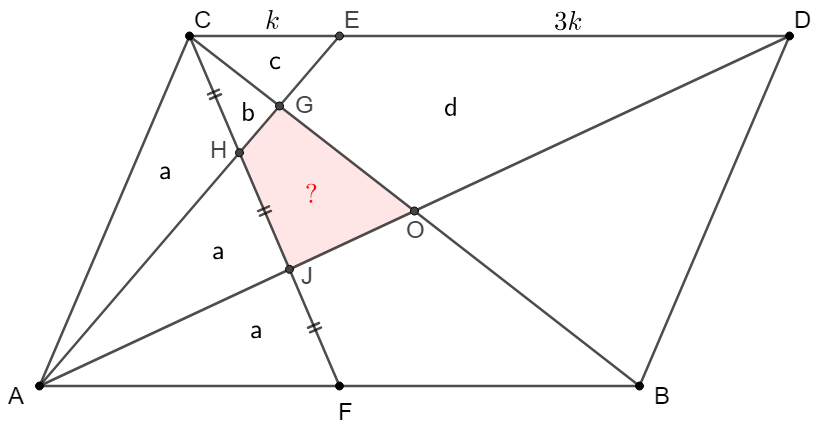 \(\begin{multline}\nonumber
\shoveleft \text{Let } [AHC]=[AHJ]=[AJF]=a, [CGH]=b, [AGE]=c, [DEGO]=d, [GHJO]=x\\
\shoveleft [CJD]=8[CHE]\implies 8(b+c)=x+d+b+c\implies d+x=7(b+c)\\
\shoveleft [ADE]=3[ACE]\implies a+d+x=3(a+b+c)\implies a+7(b+c)=3(a+b+c)\implies a=2(b+c)\\
\shoveleft [ACO]=[CDO]\implies c+d=2a+b+x \implies d-x=4(b+c)+b-c=5b+3c\\
\shoveleft \implies x=b+2c, d=6b+5c, [ACO]=\dfrac{[ABCD]}{4}=60=6(b+c)\implies b+c=10 \implies a=20\\
\shoveleft \text{Apply Extended Cross Ladde Theorem on }\triangle{ACO}: \dfrac{1}{[ACG]}+\dfrac{1}{[ACJ]}=\dfrac{1}{[ACH]}+\dfrac{1}{[ACO]}\\
\shoveleft \implies \dfrac{1}{b+20}+\dfrac{1}{40}=\dfrac{1}{20}+\dfrac{1}{60}\implies b=4\implies c=6\implies [GHJO]=x=b+2c=\bbox[5px, border: 1px solid black]{16}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let } [AHC]=[AHJ]=[AJF]=a, [CGH]=b, [AGE]=c, [DEGO]=d, [GHJO]=x\\
\shoveleft [CJD]=8[CHE]\implies 8(b+c)=x+d+b+c\implies d+x=7(b+c)\\
\shoveleft [ADE]=3[ACE]\implies a+d+x=3(a+b+c)\implies a+7(b+c)=3(a+b+c)\implies a=2(b+c)\\
\shoveleft [ACO]=[CDO]\implies c+d=2a+b+x \implies d-x=4(b+c)+b-c=5b+3c\\
\shoveleft \implies x=b+2c, d=6b+5c, [ACO]=\dfrac{[ABCD]}{4}=60=6(b+c)\implies b+c=10 \implies a=20\\
\shoveleft \text{Apply Extended Cross Ladde Theorem on }\triangle{ACO}: \dfrac{1}{[ACG]}+\dfrac{1}{[ACJ]}=\dfrac{1}{[ACH]}+\dfrac{1}{[ACO]}\\
\shoveleft \implies \dfrac{1}{b+20}+\dfrac{1}{40}=\dfrac{1}{20}+\dfrac{1}{60}\implies b=4\implies c=6\implies [GHJO]=x=b+2c=\bbox[5px, border: 1px solid black]{16}
\end{multline}\)
10/26/2023
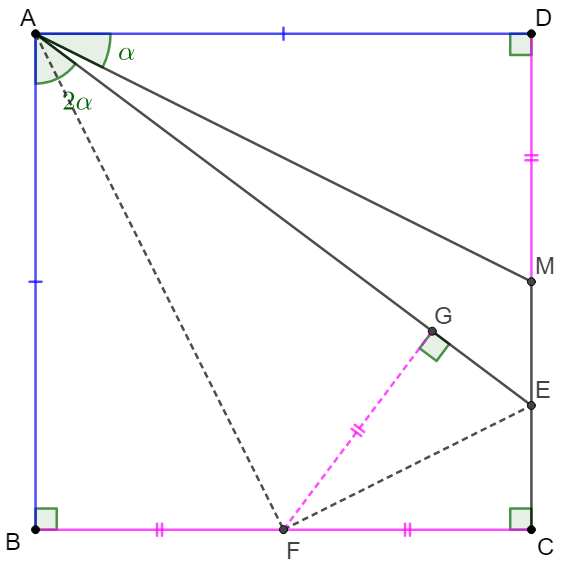
$M$ is the midpoint of side $CD$ of square $ABCD$. $E$ is also on $CD$ such that $\angle{BAE}=2\angle{MAD}$. Show that $AE=BC+CE$
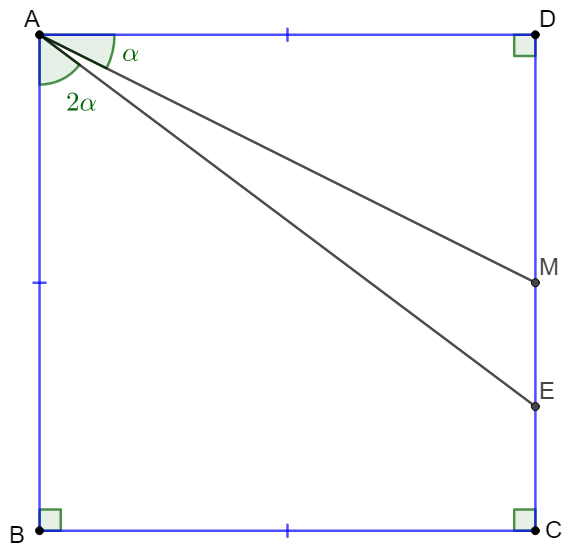
Prove:
 \(\begin{multline}\nonumber
\shoveleft \text{Let }F \text{ be the midpoint of side }BC, H \text{ on } AE \text{ such that } FG\perp AE\\
\shoveleft \implies \triangle{MAD} \cong \triangle{FAB} \implies \angle{BAF}=\angle{MAD}\implies \angle{FAG}=\angle{FAB}\\
\shoveleft \implies \triangle{FAB} \cong \triangle{FAG}\implies AG=AB=BC, BF=FG=FC\\
\shoveleft \implies \triangle{EFG} \cong \triangle{EFC}\implies CE=GE \implies AE=AG+GE=BC+CE\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }F \text{ be the midpoint of side }BC, H \text{ on } AE \text{ such that } FG\perp AE\\
\shoveleft \implies \triangle{MAD} \cong \triangle{FAB} \implies \angle{BAF}=\angle{MAD}\implies \angle{FAG}=\angle{FAB}\\
\shoveleft \implies \triangle{FAB} \cong \triangle{FAG}\implies AG=AB=BC, BF=FG=FC\\
\shoveleft \implies \triangle{EFG} \cong \triangle{EFC}\implies CE=GE \implies AE=AG+GE=BC+CE\blacksquare
\end{multline}\)
10/27/2023
$A,B,C,D,E,F$ are points on a circle such that $AD \cap BE \cap CF = O$. Let $AB=a, BC=b, CD=c, DE=d. EF=e, FA=f$, show that $ace=bdf$
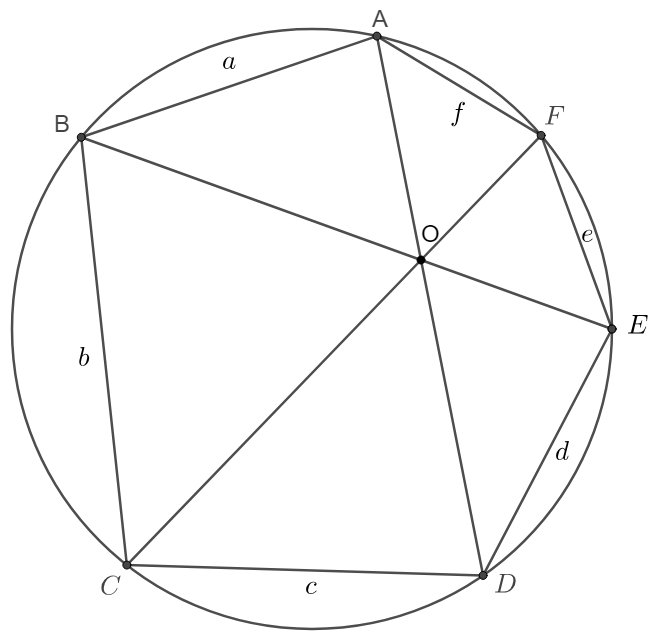
Prove:
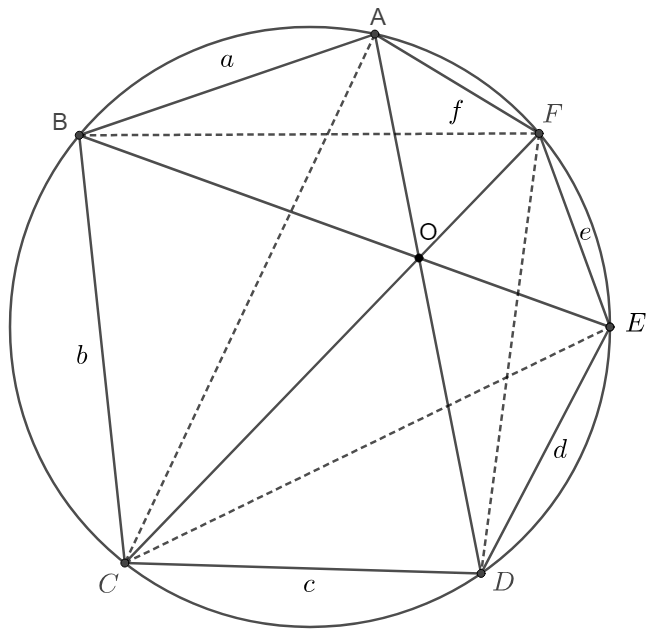 \(\begin{multline}\nonumber
\shoveleft \text{Connect } AC, BF, CE, DF. \text{Apply Ptolemy's theorem: }\\
\shoveleft a \cdot CF+bf=AC \cdot BF \implies ad\cdot CF+bdf=d \cdot AC \cdot BF\\
\shoveleft d \cdot CF + ce = CE \cdot DF \implies ad \cdot CF + ace = a \cdot CE \cdot DF\\
\shoveleft \implies bdf-ace = d \cdot AC \cdot BF - a \cdot CE \cdot DF\\
\shoveleft \text{Easy to see that }\dfrac{CE}{BF}=\dfrac{CO}{BO}, \dfrac{DF}{AC}=\dfrac{DO}{CO}, \dfrac{a}{d}=\dfrac{BO}{DO}\\
\shoveleft \implies \dfrac{a \cdot CE \cdot DF}{d \cdot AC \cdot BF}=1\implies bdf=ace\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Connect } AC, BF, CE, DF. \text{Apply Ptolemy's theorem: }\\
\shoveleft a \cdot CF+bf=AC \cdot BF \implies ad\cdot CF+bdf=d \cdot AC \cdot BF\\
\shoveleft d \cdot CF + ce = CE \cdot DF \implies ad \cdot CF + ace = a \cdot CE \cdot DF\\
\shoveleft \implies bdf-ace = d \cdot AC \cdot BF - a \cdot CE \cdot DF\\
\shoveleft \text{Easy to see that }\dfrac{CE}{BF}=\dfrac{CO}{BO}, \dfrac{DF}{AC}=\dfrac{DO}{CO}, \dfrac{a}{d}=\dfrac{BO}{DO}\\
\shoveleft \implies \dfrac{a \cdot CE \cdot DF}{d \cdot AC \cdot BF}=1\implies bdf=ace\blacksquare
\end{multline}\)
10/30/2023
Napoleon’s Theorem: if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centers of those equilateral triangles themselves form an equilateral triangle. And, the centroid of this equilateral triangle overlaps with the centroid of the original triangle.
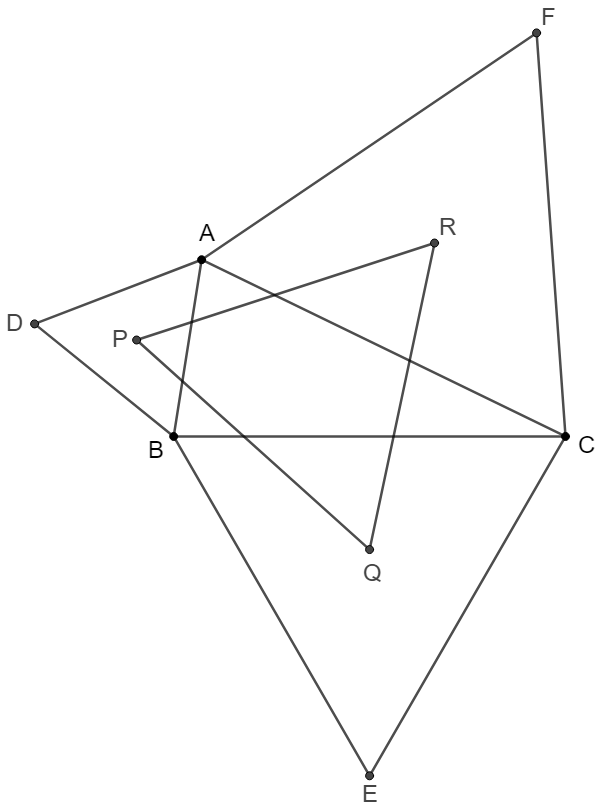
Prove 1:
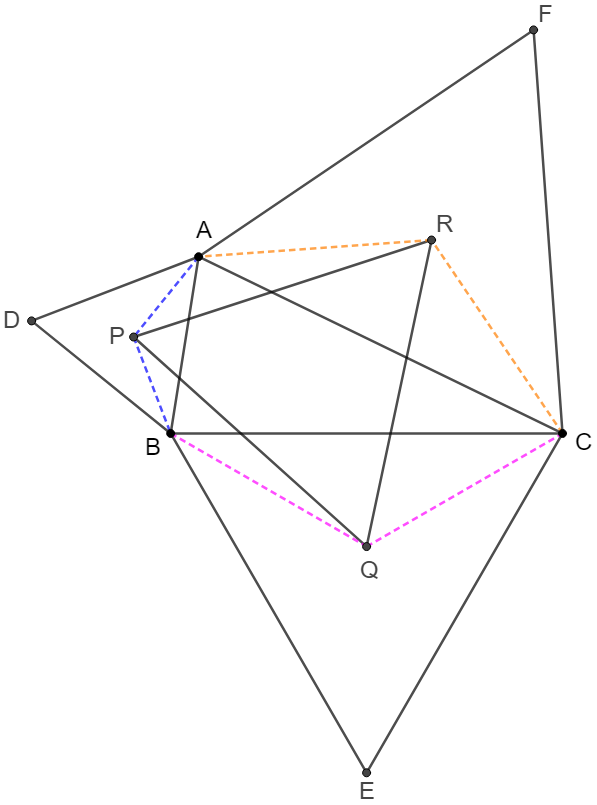 \(\begin{multline}\nonumber
\shoveleft \text{Easy to know that }AP=BP=\dfrac{c}{\sqrt{3}}, BQ=CQ=\dfrac{a}{\sqrt{3}}, CR=AR=\dfrac{b}{\sqrt{3}}\\
\shoveleft \angle{PBQ}=\angle{B+60^{\circ}}, \angle{QCR}=\angle{C+60^{\circ}}, \angle{RAP}=\angle{A+60^{\circ}}\\
\shoveleft \implies PQ^2=BP^2+BQ^2-2BP\cdot BQ\cdot cos(B+60^{\circ})\\
\shoveleft =\dfrac{c^2}{3}+\dfrac{a^2}{3}-\dfrac{2ac}{3}(cosB\cdot cos60^{\circ}-sinB\cdot sin60^{\circ})=\dfrac{a^2+c^2-ac(cosB-\sqrt{3}sinB)}{3}\\
\shoveleft =\dfrac{a^2+c^2-ac\dfrac{a^2+c^2-b^2}{2ac}+\sqrt{3}ac\cdot sinB}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft QR^2=CQ^2+CR^2-2CQ \cdot CR \cdot cos(C+60^{\circ})\\
\shoveleft =\dfrac{a^2}{3}+\dfrac{b^2}{3}-\dfrac{2ab}{3}(cosC\cdot cos60^{\circ}-sinC\cdot sin60^{\circ})=\dfrac{a^2+b^2-ab(cosC-\sqrt{3}sinC)}{3}\\
\shoveleft =\dfrac{a^2+b^2-ab\dfrac{a^2+b^2-c^2}{2ab}+\sqrt{3}ab\cdot sinC}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft RP^2=AR^2+AP^2-2AR \cdot AP \cdot cos(A+60^{\circ})\\
\shoveleft =\dfrac{b^2}{3}+\dfrac{c^2}{3}-\dfrac{2bc}{3}(cosA\cdot cos60^{\circ}-sinA\cdot sin60^{\circ})=\dfrac{b^2+c^2-bc(cosA-\sqrt{3}sinA)}{3}\\
\shoveleft =\dfrac{b^2+c^2-bc\dfrac{b^2+c^2-a^2}{2bc}+\sqrt{3}bc\cdot sinA}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft \implies PQ=QR=RP\implies \triangle{PQR} \text{ is equilateral}\\
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft \text{Easy to know that }AP=BP=\dfrac{c}{\sqrt{3}}, BQ=CQ=\dfrac{a}{\sqrt{3}}, CR=AR=\dfrac{b}{\sqrt{3}}\\
\shoveleft \angle{PBQ}=\angle{B+60^{\circ}}, \angle{QCR}=\angle{C+60^{\circ}}, \angle{RAP}=\angle{A+60^{\circ}}\\
\shoveleft \implies PQ^2=BP^2+BQ^2-2BP\cdot BQ\cdot cos(B+60^{\circ})\\
\shoveleft =\dfrac{c^2}{3}+\dfrac{a^2}{3}-\dfrac{2ac}{3}(cosB\cdot cos60^{\circ}-sinB\cdot sin60^{\circ})=\dfrac{a^2+c^2-ac(cosB-\sqrt{3}sinB)}{3}\\
\shoveleft =\dfrac{a^2+c^2-ac\dfrac{a^2+c^2-b^2}{2ac}+\sqrt{3}ac\cdot sinB}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft QR^2=CQ^2+CR^2-2CQ \cdot CR \cdot cos(C+60^{\circ})\\
\shoveleft =\dfrac{a^2}{3}+\dfrac{b^2}{3}-\dfrac{2ab}{3}(cosC\cdot cos60^{\circ}-sinC\cdot sin60^{\circ})=\dfrac{a^2+b^2-ab(cosC-\sqrt{3}sinC)}{3}\\
\shoveleft =\dfrac{a^2+b^2-ab\dfrac{a^2+b^2-c^2}{2ab}+\sqrt{3}ab\cdot sinC}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft RP^2=AR^2+AP^2-2AR \cdot AP \cdot cos(A+60^{\circ})\\
\shoveleft =\dfrac{b^2}{3}+\dfrac{c^2}{3}-\dfrac{2bc}{3}(cosA\cdot cos60^{\circ}-sinA\cdot sin60^{\circ})=\dfrac{b^2+c^2-bc(cosA-\sqrt{3}sinA)}{3}\\
\shoveleft =\dfrac{b^2+c^2-bc\dfrac{b^2+c^2-a^2}{2bc}+\sqrt{3}bc\cdot sinA}{3}=\dfrac{a^2+b^2+c^2}{6}+\dfrac{2[ABC]}{\sqrt{3}}\\
\shoveleft \implies PQ=QR=RP\implies \triangle{PQR} \text{ is equilateral}\\
\end{multline}\)
Prove 2:
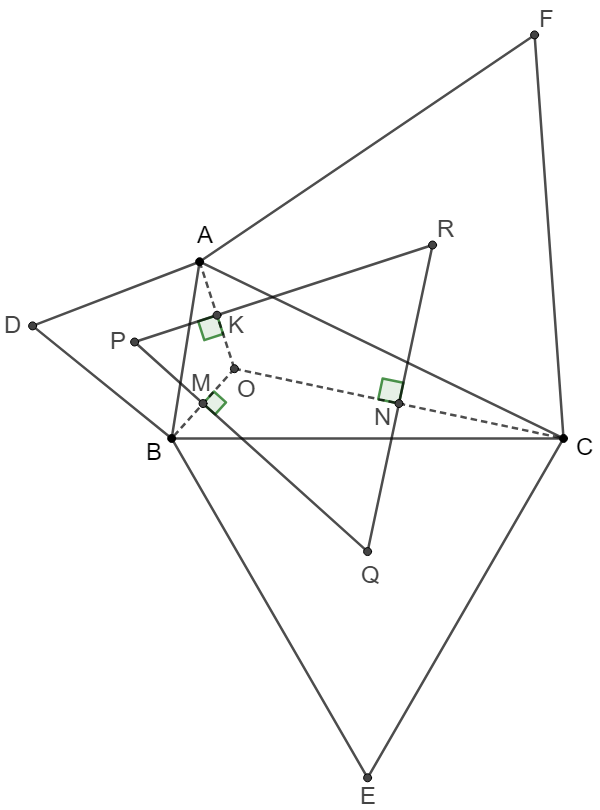 \(\begin{multline}\nonumber
\shoveleft \text{Let }O \text{ be the Fermat Point of } \triangle{ABC}\\
\shoveleft \implies \angle{AOB}=\angle{BOC}=\angle{COA}=60^{\circ}\\
\shoveleft \implies ADBO, BECO, CFAO \text{ is cyclic} \implies \\
\shoveleft \odot{ADBO} \cap \odot{BECO} = \{B, O\}\implies PQ \perp BO \text{ at } M\\
\shoveleft \odot{BECO} \cap \odot{CFAO} = \{C, O\}\implies QR \perp CO \text{ at } N\\
\shoveleft \odot{CFAO} \cap \odot{ADBO} = \{A, O\}\implies RP \perp AO \text{ at } K\\
\shoveleft \implies PMOK, QNOM, RKON \text{ is cyclic}\\
\shoveleft \implies \angle{KPM}=\angle{MQN}=\angle{NRK}=180^{\circ}-120^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{PQR} \text{ is equilateral}\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }O \text{ be the Fermat Point of } \triangle{ABC}\\
\shoveleft \implies \angle{AOB}=\angle{BOC}=\angle{COA}=60^{\circ}\\
\shoveleft \implies ADBO, BECO, CFAO \text{ is cyclic} \implies \\
\shoveleft \odot{ADBO} \cap \odot{BECO} = \{B, O\}\implies PQ \perp BO \text{ at } M\\
\shoveleft \odot{BECO} \cap \odot{CFAO} = \{C, O\}\implies QR \perp CO \text{ at } N\\
\shoveleft \odot{CFAO} \cap \odot{ADBO} = \{A, O\}\implies RP \perp AO \text{ at } K\\
\shoveleft \implies PMOK, QNOM, RKON \text{ is cyclic}\\
\shoveleft \implies \angle{KPM}=\angle{MQN}=\angle{NRK}=180^{\circ}-120^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{PQR} \text{ is equilateral}\blacksquare
\end{multline}\)
Prove 3:
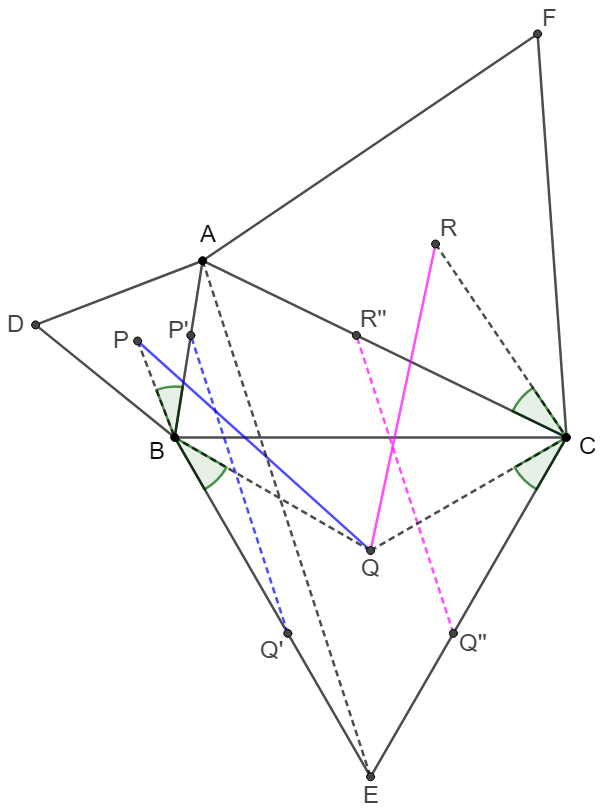 \(\begin{multline}\nonumber
\shoveleft \text{Easy to see that }\dfrac{BP}{BA}=\dfrac{BQ}{BE}=\dfrac{CR}{CA}=\dfrac{CQ}{CE}=\dfrac{1}{\sqrt{3}}\\
\shoveleft \angle{PBA}=\angle{QBE}=\angle{RCA}=\angle{QCE}=30^{\circ}\implies \\
\shoveleft \text{ Rotate }PQ \text{ around point }B \text{ and get }P'Q',\\
\shoveleft \text{ Rotate }CR \text{ around point }C \text{ and get }R''Q''\implies \\
\shoveleft \dfrac{BP'}{BA}=\dfrac{BP}{BA}=\dfrac{BQ'}{BE}=\dfrac{BQ}{BE}=\dfrac{1}{\sqrt{3}}\\
\shoveleft \dfrac{CR''}{CA}=\dfrac{CR}{CA}=\dfrac{CQ''}{CE}=\dfrac{CQ}{CE}=\dfrac{1}{\sqrt{3}} \implies\\
\shoveleft \dfrac{P'Q'}{AE}=\dfrac{R''Q''}{AE}=\dfrac{1}{\sqrt{3}}, PQ'\parallel AQ\parallel R''Q''\\
\shoveleft \implies \angle{PQR}=2\cdot 30^{\circ}=60^{\circ}, P'Q'=R''Q''\\
\shoveleft \implies PQ=RQ \implies \triangle{PQR} \text{ is equilateral} \blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Easy to see that }\dfrac{BP}{BA}=\dfrac{BQ}{BE}=\dfrac{CR}{CA}=\dfrac{CQ}{CE}=\dfrac{1}{\sqrt{3}}\\
\shoveleft \angle{PBA}=\angle{QBE}=\angle{RCA}=\angle{QCE}=30^{\circ}\implies \\
\shoveleft \text{ Rotate }PQ \text{ around point }B \text{ and get }P'Q',\\
\shoveleft \text{ Rotate }CR \text{ around point }C \text{ and get }R''Q''\implies \\
\shoveleft \dfrac{BP'}{BA}=\dfrac{BP}{BA}=\dfrac{BQ'}{BE}=\dfrac{BQ}{BE}=\dfrac{1}{\sqrt{3}}\\
\shoveleft \dfrac{CR''}{CA}=\dfrac{CR}{CA}=\dfrac{CQ''}{CE}=\dfrac{CQ}{CE}=\dfrac{1}{\sqrt{3}} \implies\\
\shoveleft \dfrac{P'Q'}{AE}=\dfrac{R''Q''}{AE}=\dfrac{1}{\sqrt{3}}, PQ'\parallel AQ\parallel R''Q''\\
\shoveleft \implies \angle{PQR}=2\cdot 30^{\circ}=60^{\circ}, P'Q'=R''Q''\\
\shoveleft \implies PQ=RQ \implies \triangle{PQR} \text{ is equilateral} \blacksquare
\end{multline}\)
Prove 1 for the centroid part:
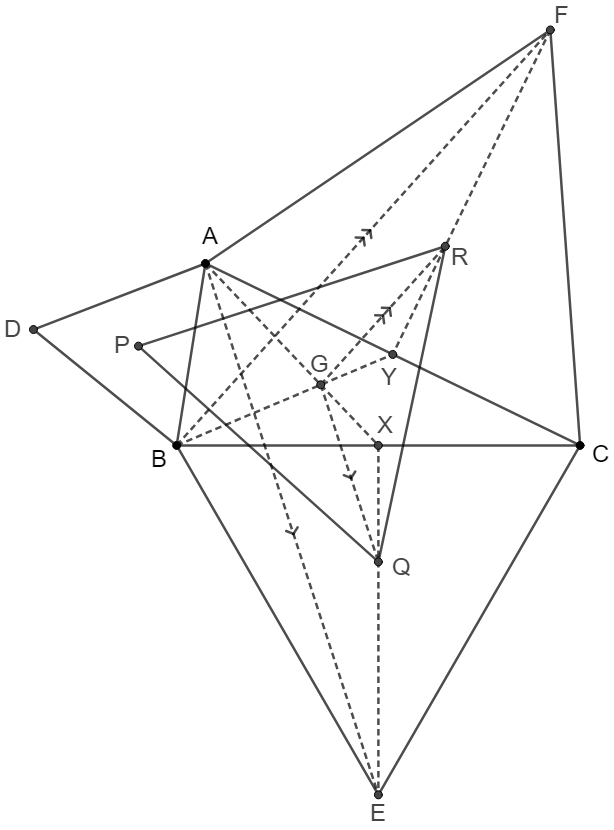 \(\begin{multline}\nonumber
\shoveleft \text{From above proof we know that } AE=\sqrt{3}PQ=BF=CD\\
\shoveleft \text{Let }G \text{ be the centroid of }\triangle{ABC}, X,Y \text{ be midpoint of side }BC, AC \text{ respectively} \\
\shoveleft \implies EQ=2QX, FR=RY, AG=2GX, BG=2GY \implies GQ=\dfrac{AE}{3}, GR=\dfrac{BF}{3}\\
\shoveleft \implies GQ=GR \text{ and similarly } GQ=GR=PG \implies G \text{ is the centroid of }\triangle{PQR} \blacksquare\\
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{From above proof we know that } AE=\sqrt{3}PQ=BF=CD\\
\shoveleft \text{Let }G \text{ be the centroid of }\triangle{ABC}, X,Y \text{ be midpoint of side }BC, AC \text{ respectively} \\
\shoveleft \implies EQ=2QX, FR=RY, AG=2GX, BG=2GY \implies GQ=\dfrac{AE}{3}, GR=\dfrac{BF}{3}\\
\shoveleft \implies GQ=GR \text{ and similarly } GQ=GR=PG \implies G \text{ is the centroid of }\triangle{PQR} \blacksquare\\
\end{multline}\)
Prove 2 for the centroid part: \(\begin{multline}\nonumber \shoveleft \text{Let }w=e^{i\tfrac{\pi}{3}}, \overrightarrow{D}=\overrightarrow{B}+w(\overrightarrow{A}-\overrightarrow{B}) \implies \overrightarrow{P}=\dfrac{\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{B}+w(\overrightarrow{A}-\overrightarrow{B})}{3}=\dfrac{\overrightarrow{A}(1+w)+\overrightarrow{B}(2-w)}{3}\\ \shoveleft \overrightarrow{Q}=\dfrac{\overrightarrow{B}(1+w)+\overrightarrow{C}(2-w)}{3}, \overrightarrow{R}=\dfrac{\overrightarrow{C}(1+w)+\overrightarrow{A}(2-w)}{3}\implies \overrightarrow{G}=\dfrac{\overrightarrow{P}+\overrightarrow{Q}+\overrightarrow{R}}{3}=\dfrac{\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{C}}{3}\blacksquare\\ \end{multline}\)
Note: Some papers about an Irish mathematician MacCool