M∀TH Workout

October 2022

 
  • Oct 06, 2022

10/06/2022

What are the last three digits of $7^{2022}$?

Solve: \(\begin{multline}\nonumber \shoveleft \text{The last three digits of }7^{2022} \text{ is the same as } (7^{2022}\mod{1000})\\ \shoveleft \text{By Euler's totient function we know:}\\ \shoveleft \implies \varphi(1000)=\varphi(2^3\cdot 5^3)=(2^3-2^2)\cdot(5^3-5^2)=400\\ \shoveleft \implies 7^{\varphi(1000)} \equiv 1 \mod{1000}\\ \shoveleft \implies 7^{400} \equiv 1 \mod{1000}\\ \shoveleft \implies 7^{2022}=7^{2000} \cdot 7^{22}=7^{2022}\cdot(50-1)^{11}\\ \shoveleft \implies 7^{2022} \mod{1000}=(50-1)^{11} \mod{1000}\\ \shoveleft \implies 7^{2022} \mod{1000}\equiv {11 \choose 9} 50^2(-1)^9+{11 \choose 10} 50(-1)^{10}+{11 \choose 11}(-1)^{11} \mod{1000}\\ \shoveleft \implies 7^{2022} \mod{1000}\equiv -500+11\cdot50-1\equiv49\mod{1000}\\ \shoveleft \implies \text{the last three digits of }7^{2022} \text{ are } \bbox[5px, border: 1px solid black]{049}. \end{multline}\) Note:

  • Fermat’s little Theorem: $p$ is prime $\implies a^p \equiv a \mod{p}$.
  • If $p$ is prime, $gcd(a,p)=1 \implies a^{p-1}\equiv 1 \mod{p}$.
  • With Euler’s totient function, $p$ is prime $\implies \varphi(p)=p-1$. If $gcd(a,p)=1 \implies a^{\varphi(n)} \equiv 1 \mod{n}$
  • $n=p_{1}^{k_1}\cdotp_{2}^{k_2}\cdot \dots\cdot p_{m}^{k_m} \implies \varphi(n)=(p_{1}^{k_1}-p_{1}^{k_1-1})(p_{2}^{k_2}-p_{2}^{k_2-1})\dots (p_{n}^{k_n}-p_{n}^{k_n-1}) \text{ where }p_i \text{ is prime for }i=1,2 \dots m$

10/11/2022

Simplify $\cfrac{1+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{3}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}$

Solve: \(\begin{multline}\nonumber \shoveleft \text{Notice } \cfrac{1+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{3}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}=\cfrac{\sqrt{2-\sqrt{1}}+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{2+\sqrt{1}}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}\\ \shoveleft \text{Generally consider }\cfrac{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n-\sqrt{k}}}}{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n+\sqrt{k}}}}, n,k \in \mathbb{N^+}, \text{easy to see that}\\ \shoveleft \Bigl(\sqrt{n-\sqrt{k}}+\sqrt{n+\sqrt{k}}\Bigr)^2= 2n+2\sqrt{n^2-k}\\ \shoveleft \implies \sqrt{n-\sqrt{k}}+\sqrt{n+\sqrt{k}}=\sqrt{2}\sqrt{n+\sqrt{n^2-k}}\\ \shoveleft \text{Now we check: } \cfrac{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n-\sqrt{k}}}}{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n+\sqrt{k}}}} = \cfrac{\displaystyle\sum_{k=1}^{n^2-1}{\Bigl(\sqrt{n-\sqrt{k}}}+\sqrt{n+\sqrt{k}}\Bigr)}{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n+\sqrt{k}}}}-1\\ \shoveleft = \cfrac{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{2}\sqrt{n+\sqrt{n^2-k}}}}{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n+\sqrt{k}}}}-1 \stackrel{i=n^2-k}{=====} \sqrt{2}\cdot \cfrac{\displaystyle\sum_{i=n^2-1}^{1}{\sqrt{n+\sqrt{i}}}}{\displaystyle\sum_{k=1}^{n^2-1}{\sqrt{n+\sqrt{k}}}}-1=\sqrt{2}-1\\ \shoveleft \text{So as special case, }n=2: \cfrac{1+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{3}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}=\bbox[5px, border: 1px solid black]{\sqrt{2}-1}\\ \end{multline}\)

10/14/2022

In quadrilateral $ABCD$, $AB \perp CD, \angle{CAB}=7^{\circ}. \angle{DAB}=23^{\circ}, \angle{ABC}=37^{\circ}$, find $\angle{BDC}$.

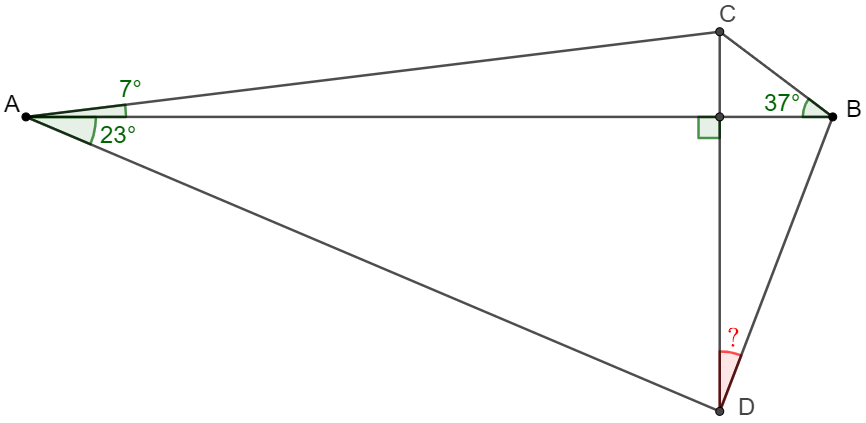
image-20221014031707768

Solve:

Make the problem into more general as following:

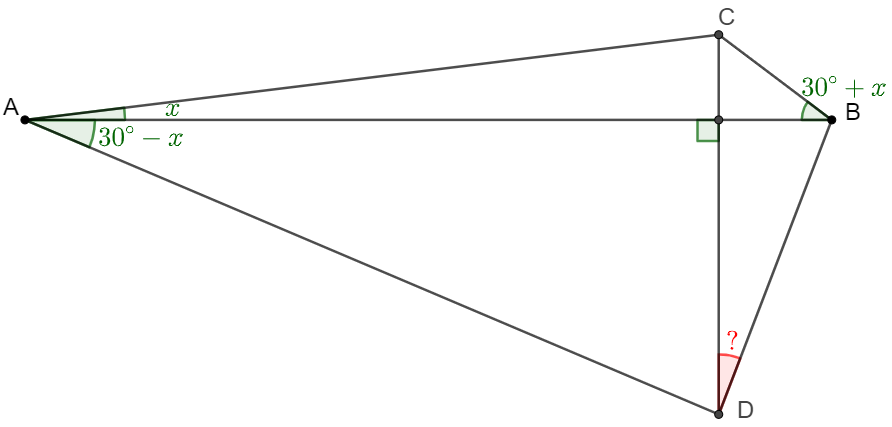
image-20221014031503805

Extend $BC$ to $E$ so that $\angle{EAC}=30^{\circ}=\angle{CAD}$, let $F$ be on $AD$ so that $EF \perp AC$. $EF$ and $AC$ intersect at $G$. Connect $BF, CF$.

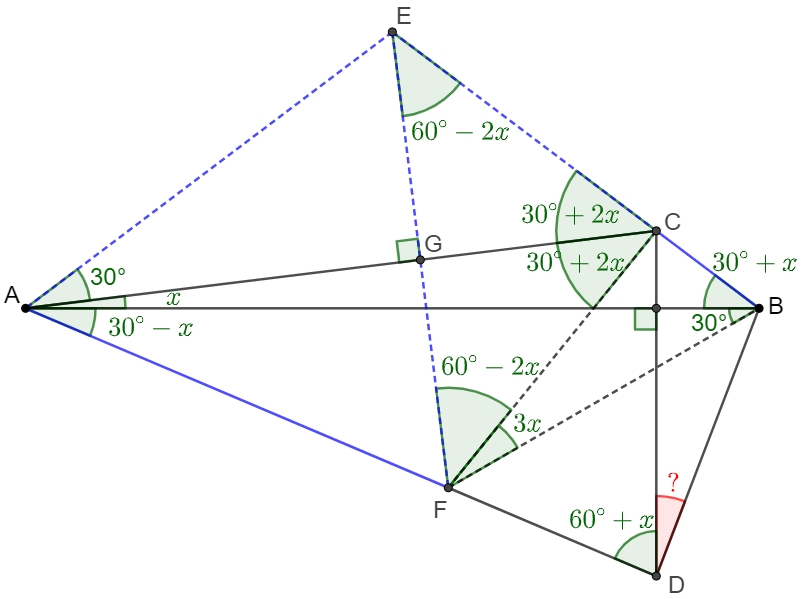
image-20221014032759371

Easy to see that \(\begin{multline}\nonumber \shoveleft \angle{ADC}=90^{\circ}-\angle{DAB}=90^{\circ}-(30^{\circ}-x)=60^{\circ}+x\\ \shoveleft \angle{ACE}=30^{\circ}+2x \implies \angle{GEC}=90^{\circ}-\angle{ACE}=60^{\circ}+2x\\ \shoveleft \angle{EAB}=30^{\circ}+x=\angle{EBA} \implies EA=EB\\ \shoveleft \angle{EAC}=\angle{FAC}=30^{\circ}, EF \perp AG \implies \triangle{AEF} \text{ is equilateral}, \triangle{AGE} \cong \triangle{AGF}\\ \shoveleft \implies CE=CF, EG=FG \implies \triangle{CEG} \cong \triangle{CFG} \implies \angle{CFE}=\angle{GEC}=60^{\circ}-2x\\ \shoveleft \implies AE=EF=EB \implies \angle{EFB}=\angle{EBF}=\cfrac{180^{\circ}-(60^{\circ}-2x)}{2}=60^{\circ}+x\\ \shoveleft \implies \angle{BFC}=\angle{EFB}-\angle{CFE}=60^{\circ}+x-(60^{\circ}-2x)=3x\\ \shoveleft \implies \angle{ADC}=\angle{EBF} \implies BCFD \text{ are cyclic} \implies \angle{BDC}=\angle{BFC}=\bbox[5px, border: 1px solid black]{3x}\\ \end{multline}\)

10/18/2022

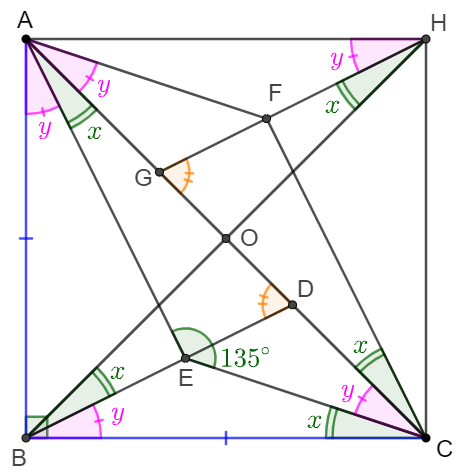
$\triangle{ABC}$ is a right isosceles triangle with $AB=BC$. $D$ is on $AC$ such that $AD=2CD$, $E$ is on $BD$ such that $\angle{AEC}=135^{\circ}$. Prove $AE \perp BD$.

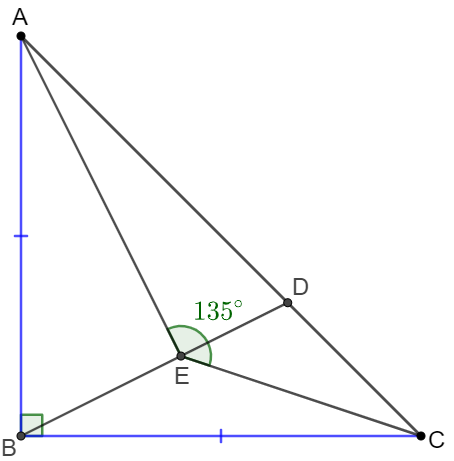
image-20221018225616914

Prove:

image-20221018225459906

10/29/2022

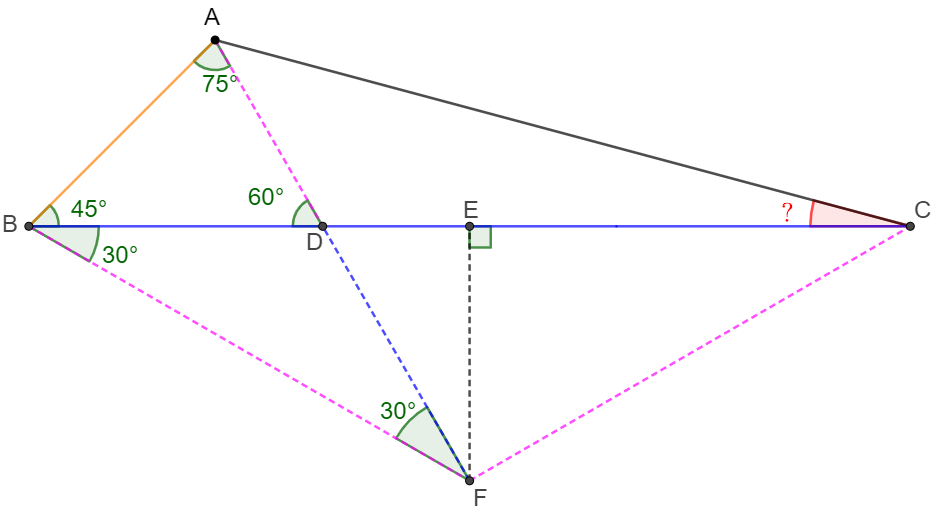
$D$ is a point on side $BC$ of $\triangle{ABC}$. $\angle{ABC}=45^{\circ}, \angle{ADB}=60^{\circ}, CD=2BD$, find $\angle{ACB}$.

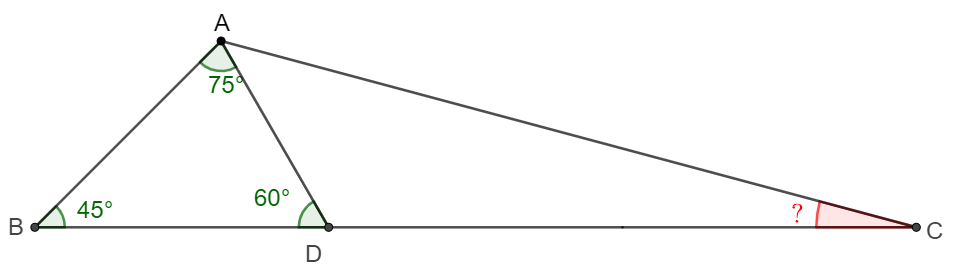
image-20221029030531943

Solve 1:

image-20221029161251469 . \(\begin{multline}\nonumber \shoveleft \text{Let } F \text{ be a point on extended } AD \text{ such that } \angle{FBC}=30^{\circ}, \text{ connect }CF\\ \shoveleft \angle{ADB}=60^{\circ} \implies \angle{DFB}=30^{\circ} \implies BD = DF\\ \shoveleft \text{and } \angle{ABF} = 45^{\circ} + 30^{\circ} = 75^{\circ} = 180^{\circ} - 45^{\circ} - 60^{\circ} = \angle{BAD} \implies AF=BF\\ \shoveleft \text{Let } E \text{ on side } BC \text{ such that } EF \perp BC, \angle{FDE} = 60^{\circ} \implies BD=DF=2 \cdot DE\\ \shoveleft \implies BE=1.5 \cdot BD = \cfrac{BC}{2}=CE \implies \triangle{BEF} \cong \triangle{CEF}\\ \shoveleft \implies BF=CF=AF, \angle{AFC}=\angle{BFC}-\angle{DFB} = 90^{\circ}\\ \shoveleft \implies \angle{FAC}=\cfrac{180^{\circ}-90^{\circ}}{2}=45^{\circ} \implies \angle{ACB}=180^{\circ}-45^{\circ}-75^{\circ}-45^{\circ}=\bbox[5px, border: 1px solid black]{15^{\circ}}\\ \end{multline}\)

Solve 2:

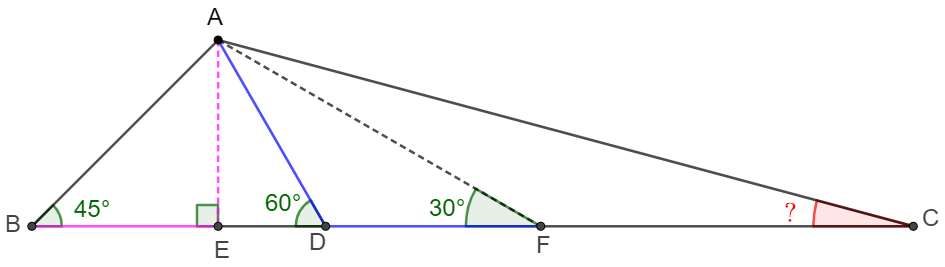image-20221102082116059 . \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ on } BD \text{ suh that } AE \perp BD, F \text{ on } EC \text{ such that } AD=DF\\ \shoveleft \implies BE=AE, DE=\cfrac{AD}{2}=\cfrac{DF}{2},\angle{DFA}=\angle{DAF}=30^{\circ}\\ \shoveleft \implies BE=AE=\cfrac{AF}{2} \implies BD=\cfrac{CD}{2} \implies BE+DE=\cfrac{DF+CF}{2} \\ \shoveleft \implies \cfrac{AF}{2} +\cfrac{DF}{2}=\cfrac{DF+CF}{2} \implies \cfrac{AF}{2}=\cfrac{CF}{2} \implies AF=CF\\ \shoveleft\implies \angle{ACB}=\cfrac{\angle{DFA}}{2}=\bbox[5px, border: 1px solid black]{15^{\circ}}\\ \end{multline}\)

    © M∀TH Workout 2020-2021
    Search