08/20/2022

Prove

\[\begin{multline} \shoveleft sin^{3}x \cdot sin3x + cos^{3}x \cdot cos3x = cos^{3}(2x)\\ \nonumber \shoveleft sin^{3}x \cdot cos 3x +cos^{3}x \cdot sin3x = \dfrac{3}{4}sin4x \\ \end{multline}\]

Prove: \(\begin{multline} \\\nonumber \shoveleft sin^3x=3sinx-4sin^3x \implies sin^3x=\dfrac{3sinx-sin3x}{4}\\ \shoveleft cos^3x=4cos^3x-3cosx \implies cos^3x=\dfrac{3cosx+cos3x}{4}\\ \shoveleft \implies sin^3x \cdot sin3x + cos^3x \cdot cos3x=\dfrac{3(sinx \cdot sin3x + cosx \cdot cos3x) +cos{^2}3x -sin{^2}3x}{4}\\ \shoveleft =\dfrac{3cos(3x-x)+cos6x}{4}=\dfrac{3cos2x+cos(3 \cdot 2x)}{4}=cos{^3}(2x)\\ \shoveleft \implies sin^3x \cdot cos3x + cos^3x \cdot sin3x=\dfrac{3(sinx \cdot cos3x + cosx \cdot sin3x)}{4}\\ \shoveleft =\dfrac{3sin(x+3x)}{4}=\dfrac{3sin4x}{4} \blacksquare{} \end{multline}\)

---

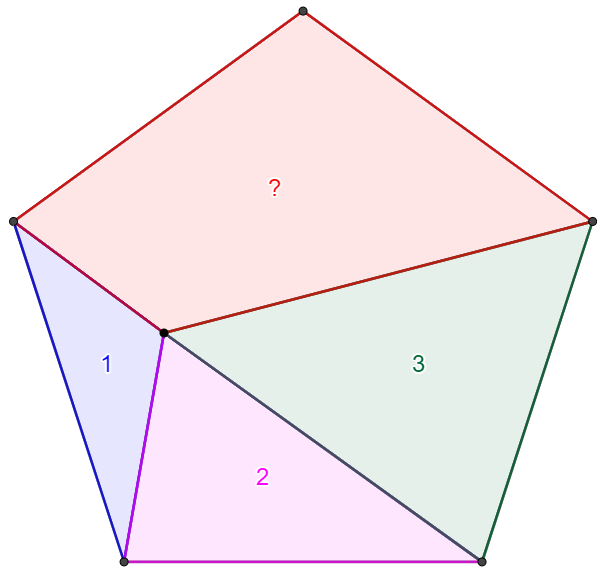
A point inside regular pentagon forms the triangles with area of $1, 2, 3$, find the area of the rest piece in the pentagon: