03/03/2021
For $\triangle{ABC}$ we know $2sinA +sinB = 2sinC$, find the minimum value for $\dfrac{5}{sinA} + \dfrac{9}{sinC}.$
Solve:
$2sinA + sinB = 2sinC \implies sinB = 2(sinC - sinA)=4cos\dfrac{A+C}{2}sin\dfrac{C-A}{2}$
$\implies sin(A+C)=2sin\dfrac{A+C}{2}cos\dfrac{A+C}{2}=4cos\dfrac{A+C}{2}sin\dfrac{C_A}{2}$
$\implies sin\dfrac{A+C}{2}=2sin\dfrac{C-A}{2}$
$\implies sin\dfrac{A}{2}cos\dfrac{C}{2} + cos\dfrac{A}{2}sin\dfrac{C}{2}=2sin\dfrac{C}{2}cos\dfrac{A}{2}-cos\dfrac{C}{2}sin\dfrac{A}{2}$
$3sin\dfrac{A}{2}cos\dfrac{C}{2} = sin\dfrac{C}{2}cos\dfrac{A}{2} \implies 3 tan\dfrac{A}{2} = tan\dfrac{C}{2}$
$\implies \dfrac{5}{sinA} + \dfrac{9}{sinC} = \dfrac{5}{\dfrac{2t}{1+t^2}} + \dfrac{9}{\dfrac{6t}{1+9t^2}}=\dfrac{16t^2+4}{t}$ where $t=tan\dfrac{A}{2}$
$\implies \dfrac{16t^2+4}{t} \le \dfrac{2 \times 4t \times 2}{t} = \bbox[1px, border: 1px solid black]{16}$
03/10/2021
If the sum of the first $n$ positive integers equals to the sum of the next $k$ positive integers, where $n<20$, what is the largest possible value of $k$?
Solve:
$\dfrac{n(n+1)}{2}=n*k+\dfrac{k(k+1)}{2}$ $\implies n^2+n=2nk+k^2+k$ $\implies (n-k)^2+(n-k)=2k^2$ $\implies 4(n-k)^2+4(n-k)+1=8k^2+1$ $\implies (2n-2k+1)^2-8k^2=1$
Let $m=2n-2k+1$, so Pell’s equation $m^2-8k^2=1$ has first solution $m=3, k=1$.
So we know the second solution has format $x+2\sqrt{2}y=(3+2\sqrt{2})^2 \implies x=17, y=6$
So $2n-2k+1=17, k=6 \implies n=14$.
The next larger value of $k$ would make $n>20$. So the answer is $k=\bbox[1px, border: 1px solid black]{6}$.
03/11/2021
Given $\triangle{ABC}$ and a point $P$ inside it, $\angle{BAP}=18^{\circ}, \angle{CAP}=30^{\circ}, \angle{ACP}=48^{\circ}, AP=BC$. Find $\angle{BCP}.$
Solve:
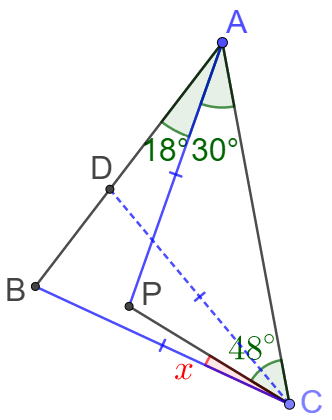
Make point $D$ on $AB$ so that $CD=AP=BC$, then $\triangle{ADC} \cong \triangle{CPA} \implies \angle{ACD}=\angle{CAP}=30^{\circ}$ $\implies \angle{CDB}=18^{\circ}+30^{\circ}+30^{\circ}=78^{\circ}$ $\implies \angle{CBD}=78^{\circ} \implies \angle{BCP}=180^{\circ}-78^{\circ}-18^{\circ}-30^{\circ}-48^{\circ}=\bbox[1px, border: 1px solid black]{6^{\circ}}$
03/13/2021
In the diagram below, $ABCD$ is a rectangle with side lengths $AB=3$ and $BC=11$, and $AECF$ is a rectangle with side lengths $AF=7$ and $FC=9,$ as shown. The area of the shaded region common to the interiors of both rectangles is $\dfrac {m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$. (Problem 2 AIME I 2021)
Solve:
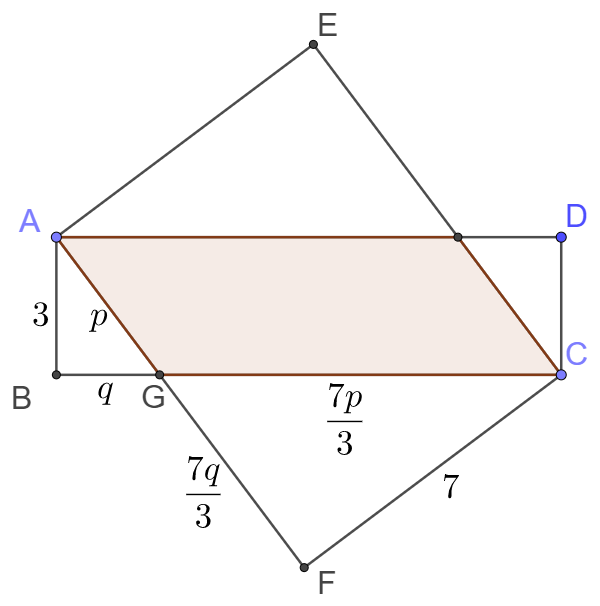
Easy to see that $\triangle{ABG} \sim \triangle{CFG} \implies AG=p, BG=q, CG=\dfrac{7p}{3}, FG=\dfrac{7q}{3}$
$BG+CG=q+\dfrac{7p}{3}=11, AG+FG=p+\dfrac{7q}{3}=9 \implies p+q=6$
$\implies \dfrac{4}{3}p=5 \implies p=\dfrac{15}{4} \implies S_{AGCD}=7p=\dfrac{105}{4} \implies m+n=\bbox[1px, border: 1px solid black]{109}$
03/14/2021
Segments $\overline{AB}, \overline{AC},$ and $\overline{AD}$ are edges of a cube and $\overline{AG}$ is a diagonal through the center of the cube. Point $P$ satisfies $PB=60\sqrt{10}, PC=60\sqrt{5}, PD=120\sqrt{2},$ and $PG=36\sqrt{7}$. What is $PA$? (Problem 6 AIME I 2021)
Solve:
03/15/2021
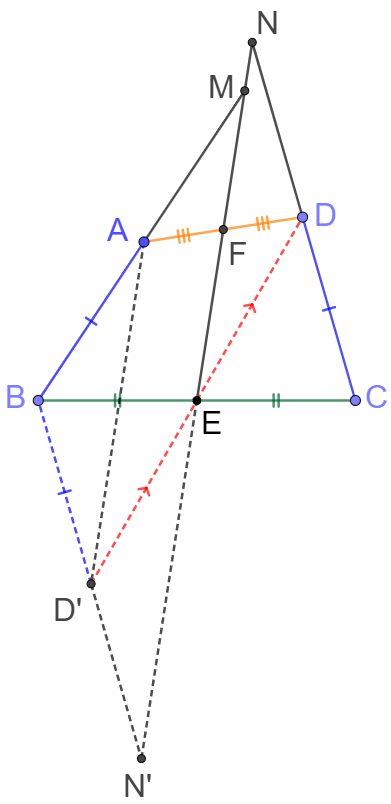
In quadrilateral $ABCD$, $AB=CD$, and points $E, F$ are midpoints of $BC, AD$ respectively. Extend $EF, CD, BA$ and they intersect at point $M,N$ as shown in following figure. Prove: $AM=DN$
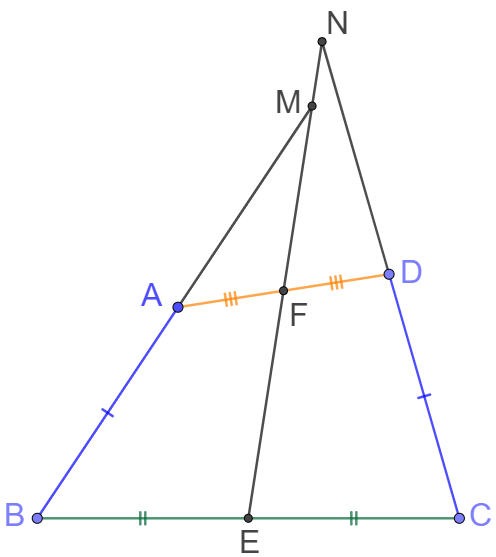
Prove 1:
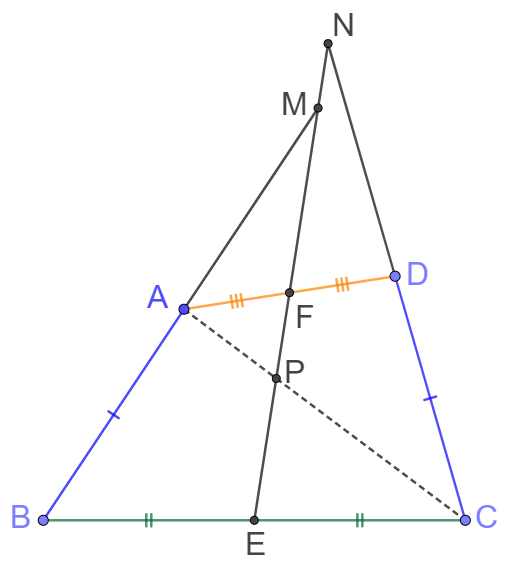
Prove 2:
03/16/2021
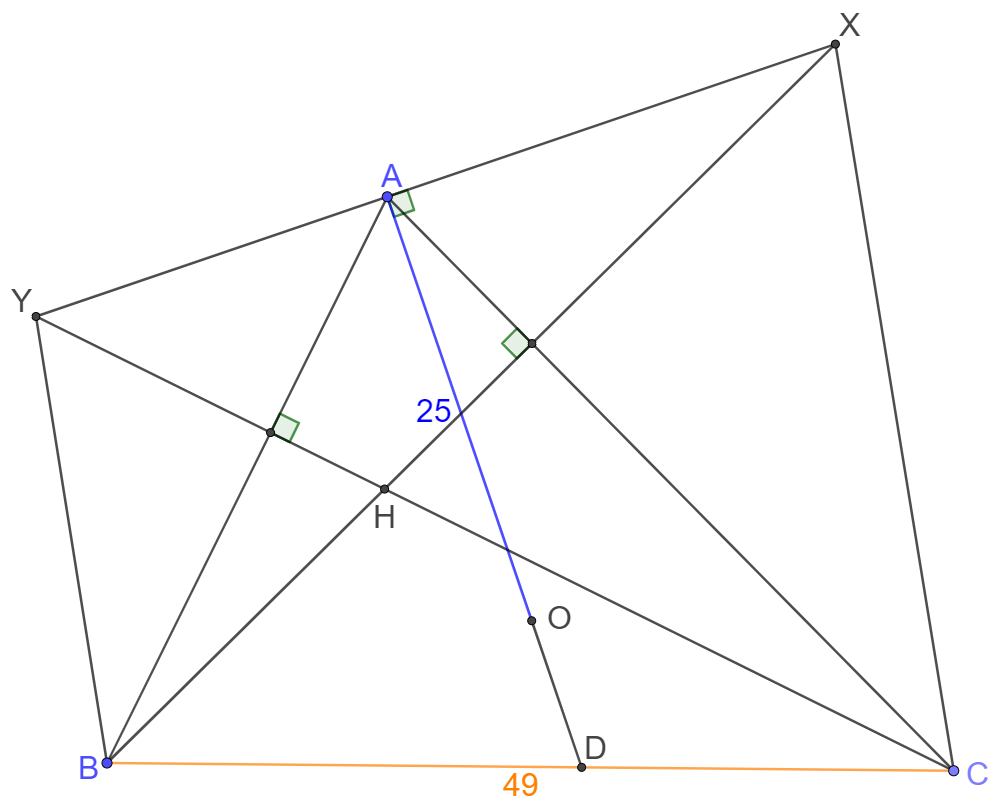
Let $\triangle{ABC}$ be an acute triangle with orthocenter $H$ and circumcenter $O$. The tangent to the circumcenter of $\triangle{ABC}$ at $A$ intersects lines $BH$ and $CH$ at $X$ and $Y$. Let line $AO$ intersect $BC$ at $D$. Suppose that $AO=25, BC=49$, and $BY \parallel CY$. Then $AD$ can be written in the form $a-b\sqrt{c}$ for positive integers $a,b,c$, where $c$ is not divisible by the square of any prime. Find $a+b+c.$
03/29/2021
Quadrilateral $ABCD$ has $\angle{ACD}=25^{\circ}, \triangle{ACB}=75^{\circ}, \angle{ABD}=30^{\circ}, BC=CD$. Circumcircle of $\triangle{ACD}$ and Extended $CB$ intersects at $E$. Prove: $BD=CE$
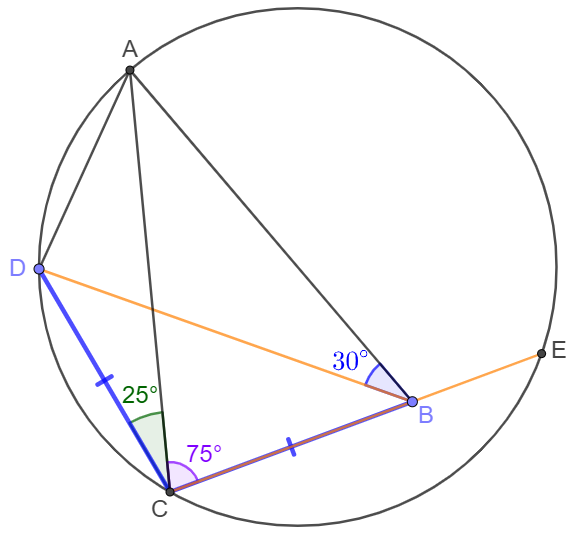
Prove:
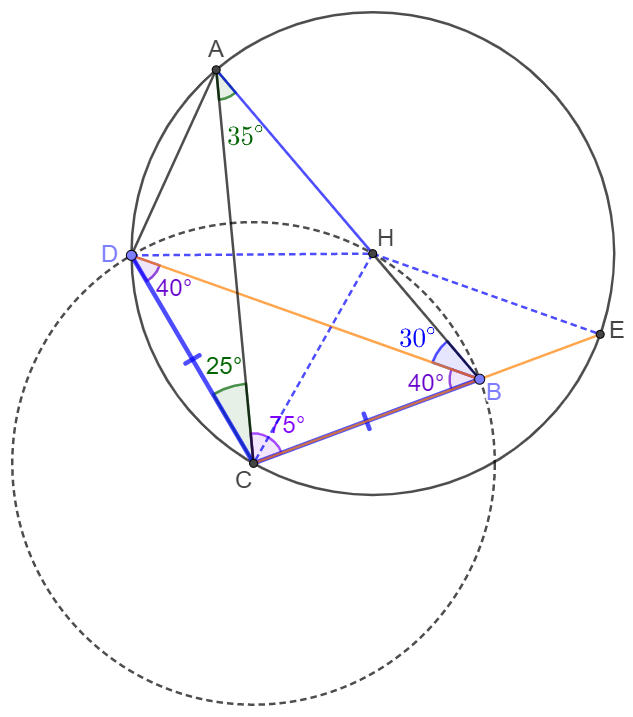
Make the circle centered at $C$ with radius $CB$. Let circle $C$ and $AB$ intersect at $H$. $BC=CD \implies D$ is on circle $C$.
$\angle{BCD}=25^{\circ}+75^{\circ}, BC=CD \implies \angle{CDB}=\angle{CBD}=40^{\circ}$
$\implies \angle{CBH}=70^{\circ}, CB=CH \implies \angle{BCH}=40^{\circ}$
$\implies \angle{ACH}=75^{\circ}-40^{\circ}=35^{\circ} \implies \angle{DCH}=25^{\circ}+35^{\circ}=60^{\circ}$
$\implies \triangle{DCH}$ is equilateral $\implies DH=CH$
and $\angle{CAB}=180^{\circ}-\angle{ABC}-\angle{ACB}=180^{\circ}-70^{\circ}-75^{\circ}=35^{\circ}=\angle{ACH}$
$\implies CH=AH \implies H$ is the center of circumcircle of $\triangle{ACD} \implies CH=HE$
so in $\triangle{BCD}$ and $\triangle{HCE}$ we have $CB=CD=CH=CE, \angle{CBD}=40^{\circ}=\angle{HCE}$
$\implies \triangle{BCD} \cong \triangle{CHE} \implies BD=CE \blacksquare$
03/30/2021
In $\triangle{ABC}, \angle{BAC}=45^{\circ}, AD \perp BC, BD=2, CD=3$, find $AD$.
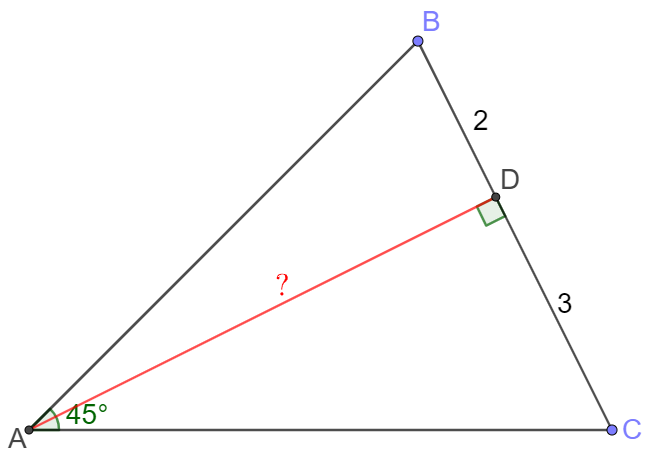
Solve:
Make $DE \perp AB$ at $E$, $CF \perp AB$ at $F$, let $BE=2x, DE=2y$, easy to see that $EF=3x, CF=5y, x^2+y^2=1$
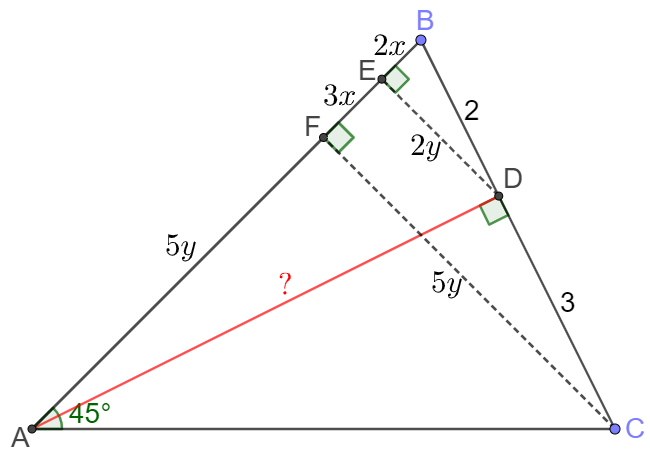
In $\triangle{ABD}$ we have $DE^2=BE \cdot AE \implies (2y)^2=2x(3x+5y)$
$\implies 3x^2+5xy-2y^2=0 \implies (3x-y)(x+2y)=0$
$\implies y=3x \implies x^2+9x^2=1 \implies x=\dfrac{1}{\sqrt{10}} \implies y=\dfrac{3}{\sqrt{10}}$
$\implies AD=\dfrac{AB \cdot CF}{BC}=\dfrac{5y(5x+5y)}{5}=5y(x+y)=\dfrac{15}{\sqrt{10}}\dfrac{4}{\sqrt{10}}=\bbox[1px, border: 1px solid black]{6}$
03/31/2021
Solve for real values of $x$: $2\sqrt[3]{2x+1}=x^3-1$.
Solve:
Let $y^3=2x+1 \implies x=\dfrac{y^3-1}{2}$ $\implies 2y=x^3-1 \implies y=\dfrac{x^3-1}{2}$
This means the solutions of the original equation are the intersects of $y=x$ and $y=\dfrac{x^3-1}{2}$
$\implies x=\dfrac{x^3-1}{2} \implies x^3-2x-1=0$
Easy to see that $x=-1$ is one of the solutions, factorize $x^3-2x-1$ and get:
$(x+1)(x^2-x-1)=0 \implies x=\bbox[1px, border: 1px solid black]{-1, \dfrac{1+\sqrt{5}}{2}, \dfrac{1-\sqrt{5}}{2}}$