02/04/2026
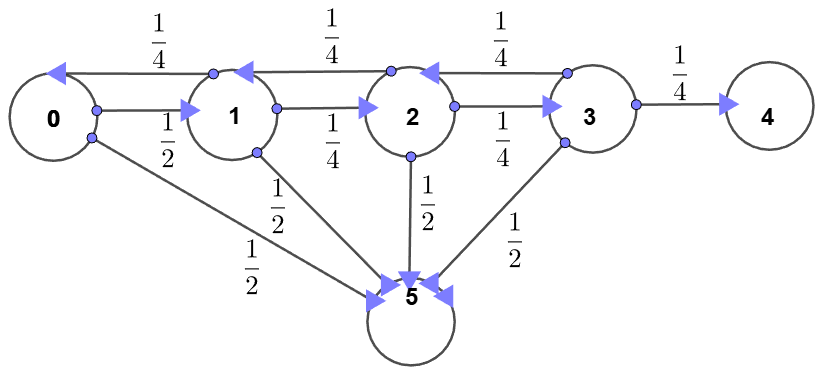
2025 AMC 12B Problem 20 A frog hops along the number line according to the following rules:
- It starts at $0$.
- If it is at $0$, then it moves to $1$ with probability $\frac{1}{2}$ and disappears with probability $\frac{1}{2}$
- For $n=1,2,3$, if it is at $n$, then it moves to $n+1$ with probability $\frac{1}{4}$, to $n-1$ with probability $\frac{1}{4}$, and disappears with probability $\frac{1}{2}$.
What is the probability that the flog reaches $4$?
solve:
 \(\begin{multline}
\shoveleft \text{Let } 5 \text{ to be the appoint of disappearing in state transfer diagram}\\
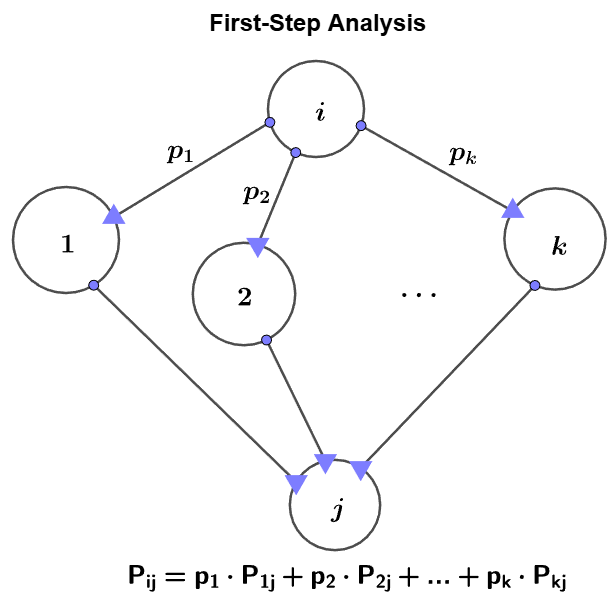
\shoveleft P_{ij} \text{ to be the hitting probability the frog starts from point }i \text{ and reaches point }j\\
\shoveleft \implies P_{00}=0, P_{11}=0, P_{22}=0, P_{33}=0, P_{44}=1, P_{54}=0\\
\shoveleft \text{Apply First-Step Analysis }\implies P_{04}=\dfrac{1}{2}P_{54}+\dfrac{1}{2}P_{14}=\dfrac{1}{2}P_{14}\\
\shoveleft P_{14}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{24}+\dfrac{1}{4}P_{04}=\dfrac{1}{4}P_{24}+\dfrac{1}{4}P_{04}\\
\shoveleft P_{24}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{34}+\dfrac{1}{4}P_{14}=\dfrac{1}{4}P_{34}+\dfrac{1}{4}P_{14}\\
\shoveleft P_{34}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{44}+\dfrac{1}{4}P_{24}=\dfrac{1}{4}+\dfrac{1}{4}P_{24} \implies P_{04}=\bbox[5px, border: 1px solid black]{\dfrac{1}{97}}\\
\end{multline}\)
Note:
\(\begin{multline}
\shoveleft \text{Let } 5 \text{ to be the appoint of disappearing in state transfer diagram}\\
\shoveleft P_{ij} \text{ to be the hitting probability the frog starts from point }i \text{ and reaches point }j\\
\shoveleft \implies P_{00}=0, P_{11}=0, P_{22}=0, P_{33}=0, P_{44}=1, P_{54}=0\\
\shoveleft \text{Apply First-Step Analysis }\implies P_{04}=\dfrac{1}{2}P_{54}+\dfrac{1}{2}P_{14}=\dfrac{1}{2}P_{14}\\
\shoveleft P_{14}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{24}+\dfrac{1}{4}P_{04}=\dfrac{1}{4}P_{24}+\dfrac{1}{4}P_{04}\\
\shoveleft P_{24}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{34}+\dfrac{1}{4}P_{14}=\dfrac{1}{4}P_{34}+\dfrac{1}{4}P_{14}\\
\shoveleft P_{34}=\dfrac{1}{2}P_{54}+\dfrac{1}{4}P_{44}+\dfrac{1}{4}P_{24}=\dfrac{1}{4}+\dfrac{1}{4}P_{24} \implies P_{04}=\bbox[5px, border: 1px solid black]{\dfrac{1}{97}}\\
\end{multline}\)
Note: