M∀TH Workout

January 2026

 
  • Jan 07, 2026

01/07/2026

$\triangle{ABC}, \triangle{ADE}, \triangle{AFG}$ are equilateral triangles. $K, M, N$ are the midpoint of $BD, EF, CG$ respectively. Show that $\triangle{KMN}$ is equilateral.

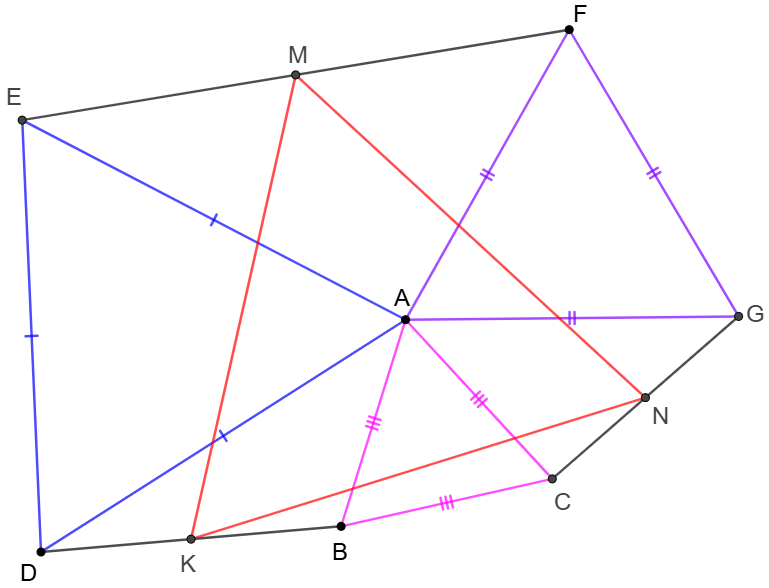
image-20260107004221466

Prove:

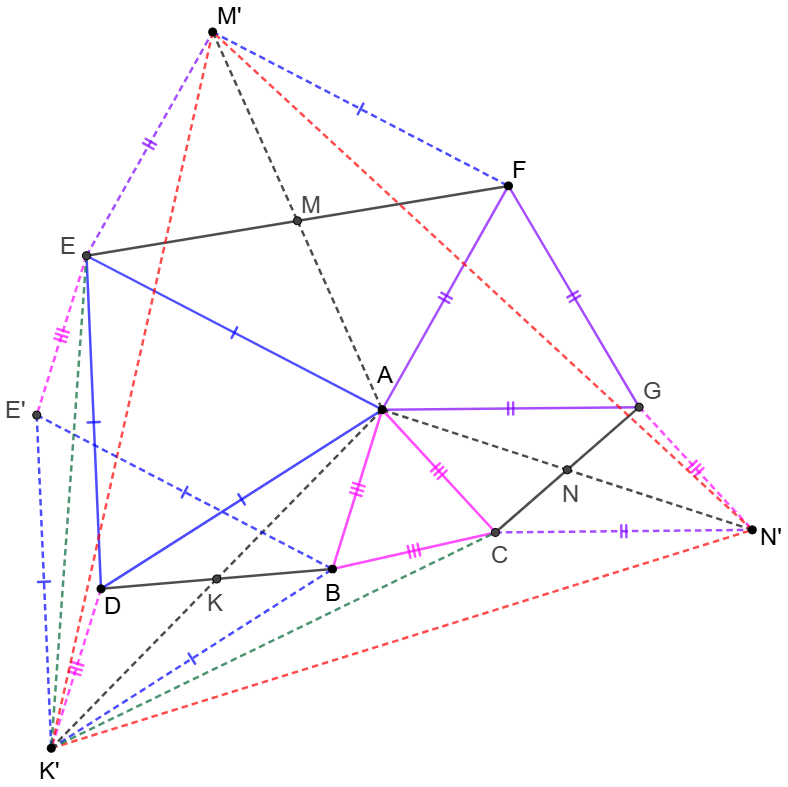image-20260107004501724 \(\begin{multline} \shoveleft \text{Extend }AK, AM, AN \text{ to }K', M', N'\\ \shoveleft \text{ such that }KK'=AK, MM'=AM, NN'=AN\\ \shoveleft \implies AGN'C, ADK'B, AEM'F \text{ are all parallelograms}\\ \shoveleft \text{Then make }ABE'E \text{ to be parallelogram}\\ \shoveleft \implies ABK'D, DK'E'E \text{ are also parallelograms}\\ \shoveleft \implies \triangle{BK'E'} \text{ is also equilateral triangle}\\ \shoveleft \implies BK'=E'K', E'E=AB=BC, \angle{KBC}=240^{\circ}-\angle{ABE'}\\ \shoveleft =60^{\circ}+(180^{\circ}-\angle{ABE'})=60^{\circ}+\angle{EE'K'}=\angle{EE'K'}\\ \shoveleft \implies \triangle{EE'K'}\cong\triangle{CBK'}\implies EK'=CK', \angle{E'EK'}=\angle{BCK'}\\ \shoveleft \implies \angle{K'CN'}=300^{\circ}-\angle{BCK'}-\angle{ACN'}=120^{\circ}+\angle{CAG}-\angle{E'EK'}\\ \shoveleft = \angle{BAF}-\angle{E'EK'}=\angle{E'EM'}-\angle{E'EK'}=\angle{K'EM'}\\ \shoveleft CN'=AG=AF=EM' \implies \triangle{M'EK'}\cong\triangle{N'CK'}\\ \shoveleft \implies M'K'=N'K',\angle{EK'M'}=\angle{CK'N'} \implies \triangle{K'M'N'} \text{ is equilateral}\\ \shoveleft \implies \triangle{KMN} \text{ is equilateral triangle}\blacksquare \end{multline}\)

01/19/2026

$P$ is a point on the incircle of equilateral triangle $\triangle{ABC}$ and $PB=1, PC=\sqrt{7}$, find the radius of the incircle.

Solve: \(\begin{multline} \shoveleft \text{Let }PA=a, PB=b, PC=c, AB=s \\ \shoveleft \implies \text{The radius of the incircle }r=\dfrac{s}{2\sqrt{3}}\\ \shoveleft \text{Since }P \text{ is inside equilateral triangle}\implies\\ \shoveleft 3(a^4+b^4+c^4+s^4)=(a^2+b^2+c^2+s^2)^2\\ \shoveleft \text{Since }P \text{ is on the incircle of equilateral triangle}\\ \shoveleft \implies a^2+b^2+c^2=\dfrac{5}{4}s^2 \implies a^2=\dfrac{5}{4}s^2-(b^2+c^2)\\ \shoveleft \implies 7s^4-20(b^2+c^2)s^2+16(b^4+c^4+b^2c^2)=0\\ \shoveleft \implies s^2=\dfrac{10(b^2+c^2)\pm2\sqrt{22b^2c^2-3(b^4+c^4)}}{7}\\ \shoveleft b=1,c=\sqrt{7}\implies s^2=\dfrac{80\pm4}{7}\\ \shoveleft \implies s=\sqrt{12} \text{ or }s=\sqrt{\dfrac{76}{7}}\\ \shoveleft \implies r=\dfrac{s}{2\sqrt{3}}=\bbox[5px, border: 1px solid black]{1} \text{ or }\bbox[5px, border: 1px solid black]{\sqrt{\dfrac{19}{21}}} \end{multline}\) Note:

01/23/2026

$ABCD$ is a quadrilateral such that $\angle{ABD}=6^{\circ}$, $\angle{CBD}=\angle{ACB}=30^{\circ}$, $\angle{ACD}=24^{\circ}$, $AC\cap BD=E$, find $\angle{CAD}$

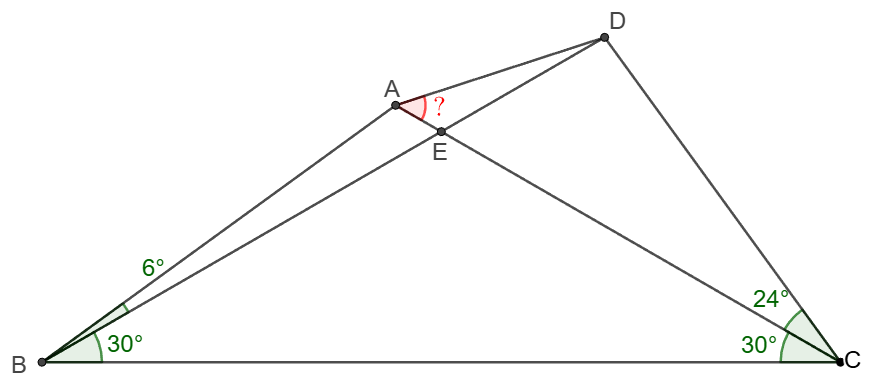
image-20260123000819865

Solve:

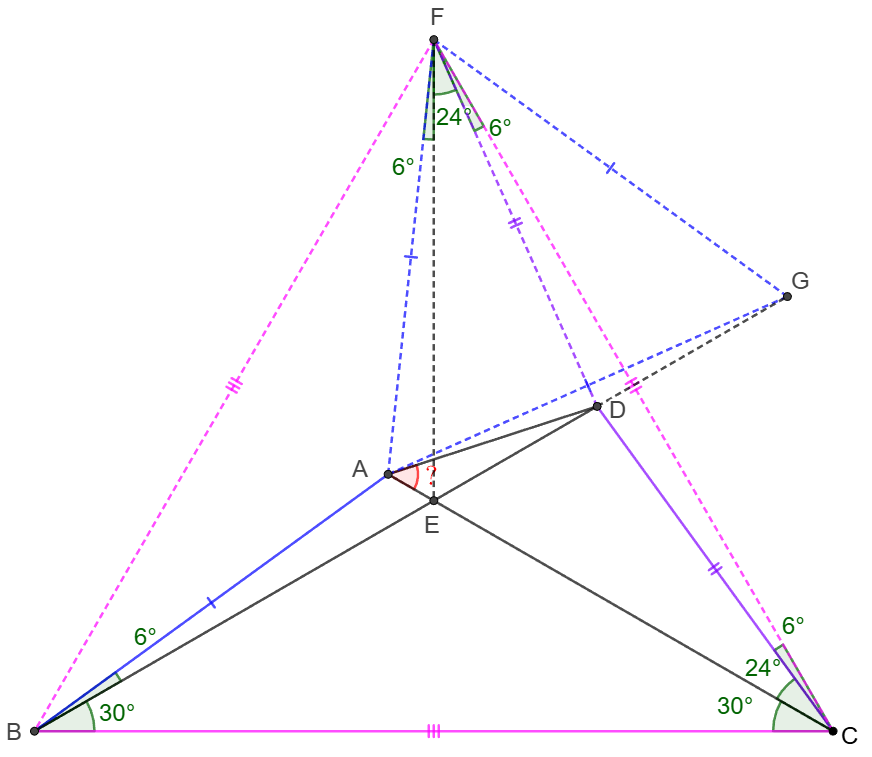image-20260123001338363 \(\begin{multline} \shoveleft \text{Let }F \text{ be the reflection of point }B \text{ along }AC \implies \\ \shoveleft \triangle{BCF}\text{ is equilateral }, AB=AF, \angle{AFE}=\angle{ABE}=6^{\circ}\\ \shoveleft BE=CE=FE, \angle{CFE}=\angle{CBE}=\angle{ECF}=\angle{BCE}=30^{\circ}\\ \shoveleft \implies CD=CF, \angle{DCF}=\angle{DFC}=6^{\circ}\implies \angle{DFE}=24^{\circ}\\ \shoveleft \text{Extend }BD \text{ to }G \text{ such that }AB=AG\implies AG=AF\\ \shoveleft \angle{AGB}=\angle{ABG}=6^{\circ}=\angle{AFE} \implies AFGE \text{ is cyclic}\\ \shoveleft \implies \angle{FAG}=\angle{FEG}=60^{\circ}\implies AFG \text{ is equilateral}\\ \shoveleft \implies \angle{AFG}=60^{\circ}\implies \angle{AFD}=30^{\circ}=\angle{GFD}, AF=GF\\ \shoveleft \implies \triangle{AFD}\cong\triangle{GFD}\implies AD=GD\implies\\ \shoveleft \angle{DAG}=\angle{DGA}=6^{\circ}\implies \angle{ADE}=12^{\circ}\\ \shoveleft \implies \angle{CAD}=\angle{CED}-\angle{ADE}=60^{\circ}-12^{\circ}=\bbox[5px, border: 1px solid black]{48^{\circ}}\\ \end{multline}\)

01/24/2026

$D,E,F$ are points on side $AB, BC, CA$ of $\triangle{ABC}$ respectively such that $\angle{CDE}=\angle{CDF}$, $\angle{AED}=\angle{AEF}$, $\angle{CFD}=\angle{CFE}$, show that $AE, BF, CD$ are altitudes of $\triangle{ABC}$.

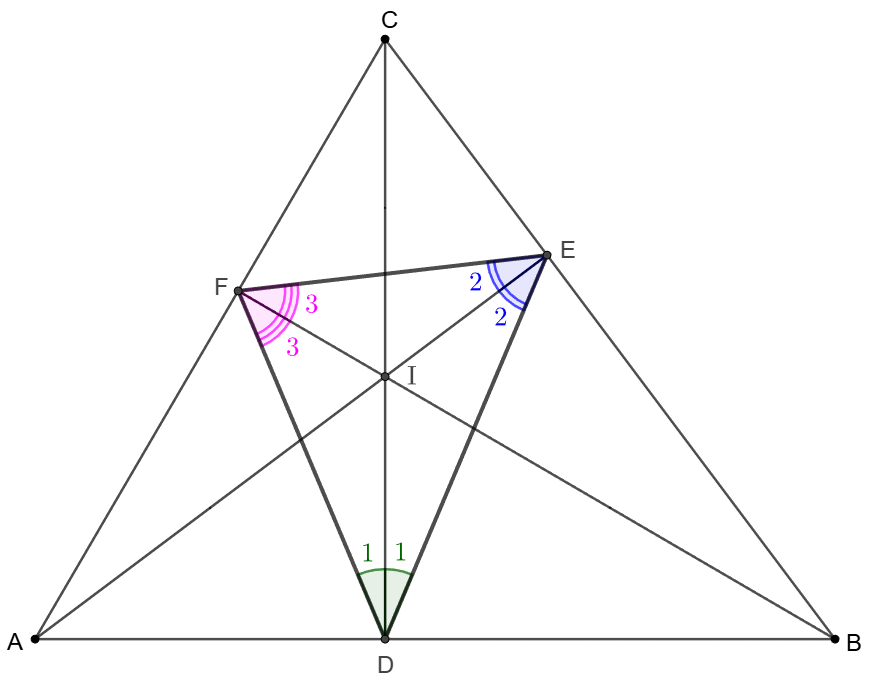
image-20260124135613779

Prove:

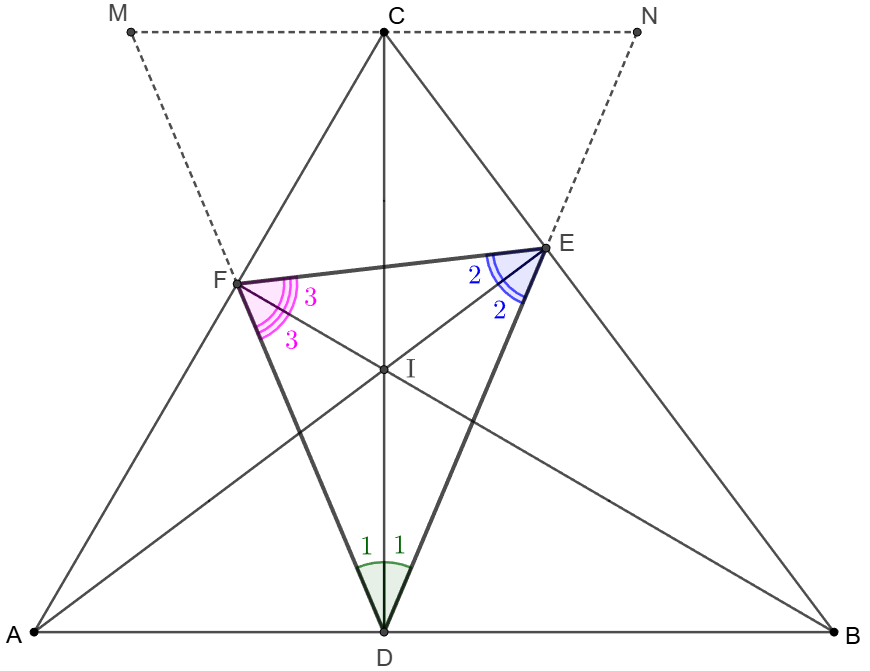image-20260124140050708 \(\begin{multline} \shoveleft \text{Extend }DE, DF \text{ to }M,N \text{ such that }C \text{ is on }MN, MN \parallel AB\\ \shoveleft \dfrac{CN}{BD}=\dfrac{CE}{BE}=\dfrac{[ICE]}{[IBE]}=\dfrac{[IAC]}{[IAB]}\implies CN=BD\cdot\dfrac{[IAC]}{[IAB]}\\ \shoveleft \text{Similarly, }CM=AD\cdot\dfrac{[IBC]}{[IAB]}, \text{and }AD=BD\cdot \dfrac{[IAC]}{[IBC]} \\ \shoveleft \implies CM=BD \cdot \dfrac{[IAC][IBC]}{[IAB][IBC]}=BD\cdot\dfrac{[IAC]}{[IAB]}=CN\\ \shoveleft \angle{CDM}=\angle{CDN}\implies \dfrac{DM}{CM}=\dfrac{DN}{CN}\\ \shoveleft \implies DM=DN\implies \triangle{CDM}\cong\triangle{CDN}\\ \shoveleft \implies CD\perp MN\implies CD \perp AB\\ \shoveleft \text{Similarly, }AE\perp BC, BF \perp AC\blacksquare\\ \end{multline}\)

Note:

This pattern has more properties here:

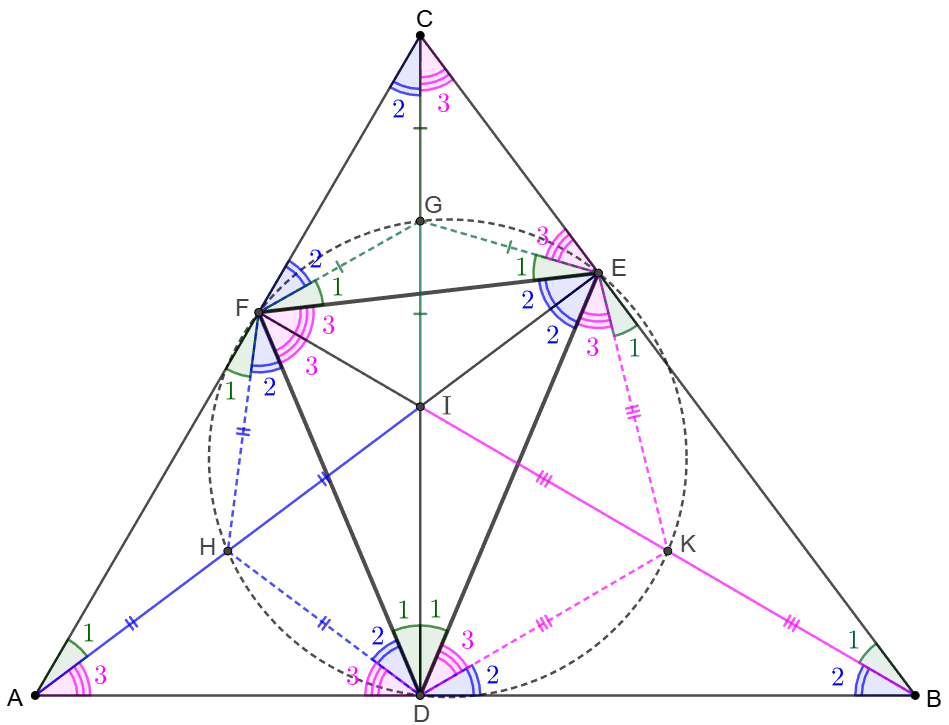
  • Let $I=AE \cap BF \cap CD$, $I$ is the incenter of $\triangle{DEF}$, the orthocenter of $\triangle{ABC}$
  • Let $G=CI \cap [DEF], H=AI \cap [DEF], K=BI \cap [DEF]$, applying $CD, AE, BF$ are altitudes and do angle chasing will give $GE=GF=GI=GC, HD=HF=HI=HA, KD=KE=KI=KB$, which means that $A=E\text{-excenter}=I_E, B=F\text{-excenter}=I_F, C=D\text{-excenter}=I_D$ , this means we have proved another format of The Incenter/Excenter Lemma without the conditions of excenters.

image-20260124141819728

01/28/2026

Nine-point Circle: prove that the midpoint of each side of the triangle, the foot of each altitude and each Euler point – the midpoint of the line segment from each vertex of the triangle to the orthocenter – are cyclic.

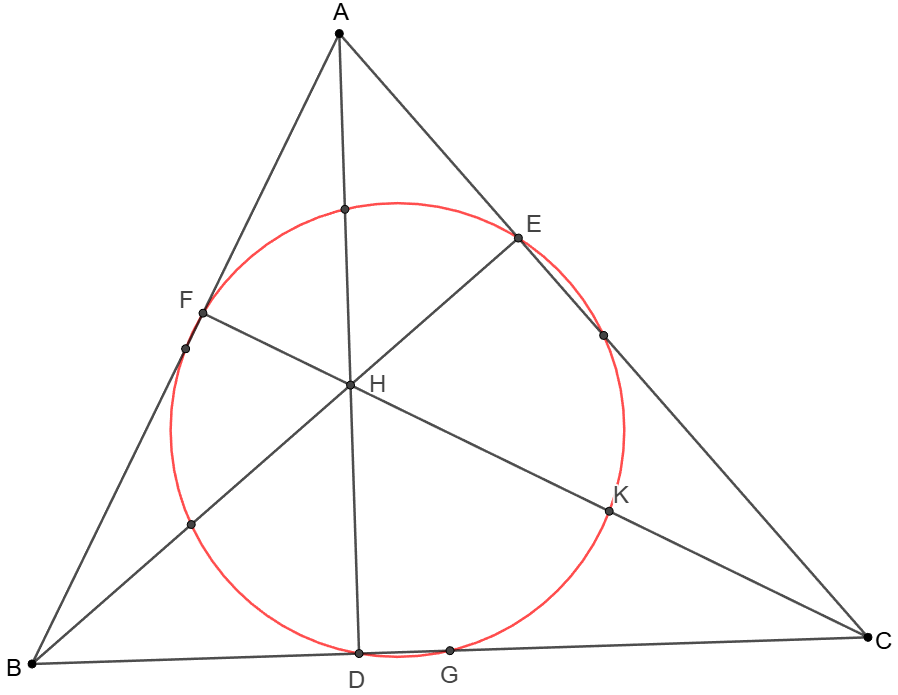
image-20260129000247904

Prove:

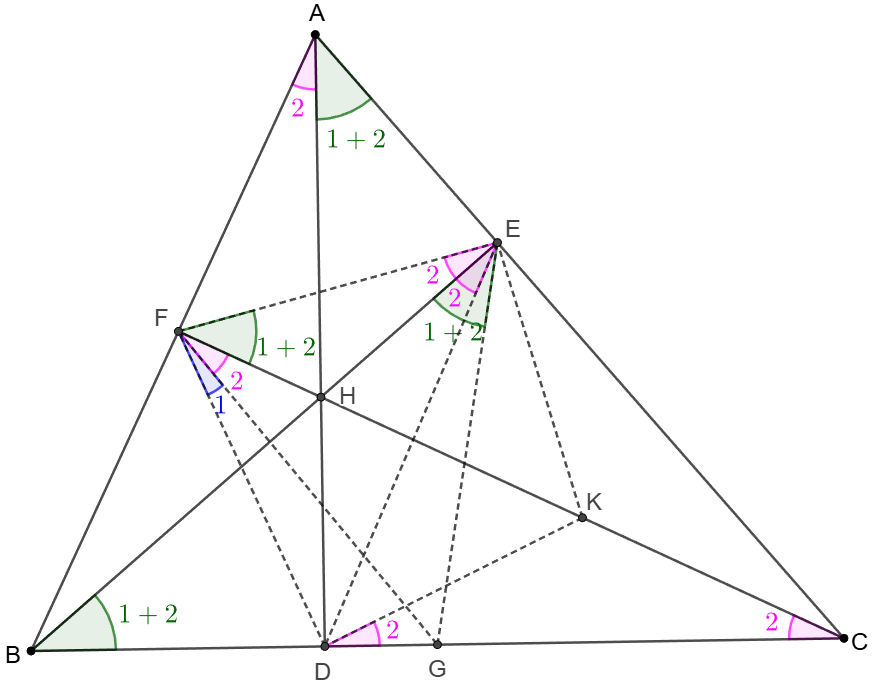image-20260128234137712 \(\begin{multline} \shoveleft \text{Let }D,E,F \text{ are foot of altitude }AD, BE, CF \text{ respectively}\\ \shoveleft AD \cap BE \cap CF =H, BG=GC, HK=KC\\ \shoveleft \text{Easy to know that }AEHF, BDHF, CDHE, ABDE, ACDF, BCEF \text{ are all cyclic }\\ \shoveleft \implies \angle{CAD}=\angle{CBE}=\angle{EFH}=\angle{DFH},\angle{BAD}=\angle{BCF}=\angle{FEH}=\angle{DEH}\\ \shoveleft BG=GC \implies \angle{CBE}=\angle{BEG}, \angle{BCF}=\angle{CFG}\\ \shoveleft \implies \angle{DFH}=\angle{BEG},\angle{CFG}=\angle{DEH}\implies \angle{DFG}=\angle{DEG}\implies EFDG \text{ is cyclic}\\ \shoveleft \implies \text{the midpoint of each side of the triangle is on the circle }[DEF]\\ \shoveleft HK=KC \implies \angle{BCF}=\angle{CDK}\implies \angle{DKF}=2\angle{BCF}=\angle{DEF}\\ \shoveleft \implies DFEK \text{ is cyclic} \implies \text{ each Euler point is also on the circle }[DEF]\blacksquare \end{multline}\)

    © M∀TH Workout 2020-2021
    Search