12/01/2025
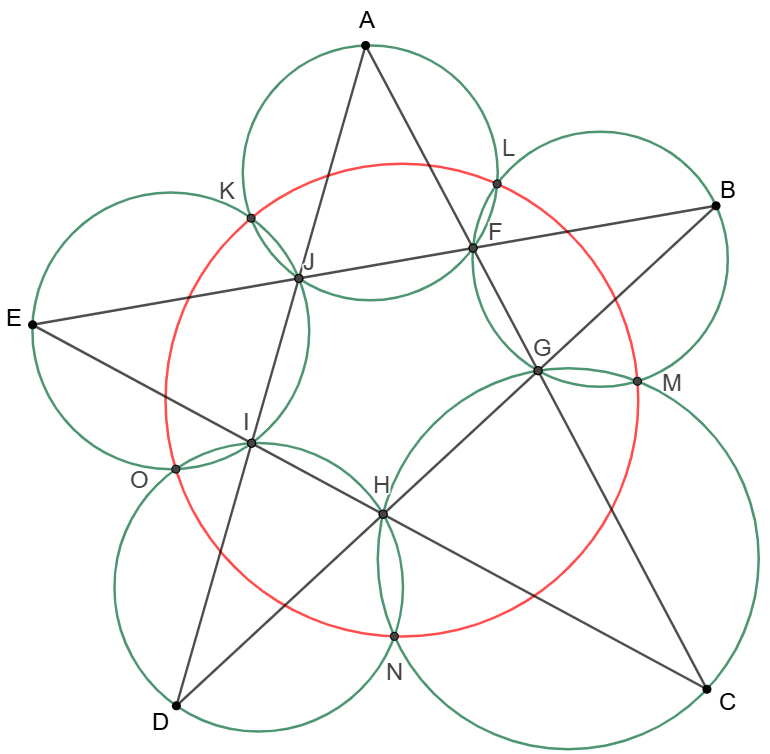
Miquel’s Pentagram Theorem : Consider a convex pentagon $FGHIJ$ extend the sides to a pentagram $ABCDE$. Externally to the pentagon, there are five triangles $\triangle{AFJ}, \triangle{BFG}, \triangle{CGH}, \triangle{DHI}, \triangle{EIJ}$. Construct the five circumcircles. Each pair of adjacent circles intersect at a vertex of the pentagon and a second point $K,L,M,N,O$. Then Miquel’s pentagram theorem states that these five second points $K,L,M,N,O$ are concyclic.
Prove:
 \(\begin{multline}
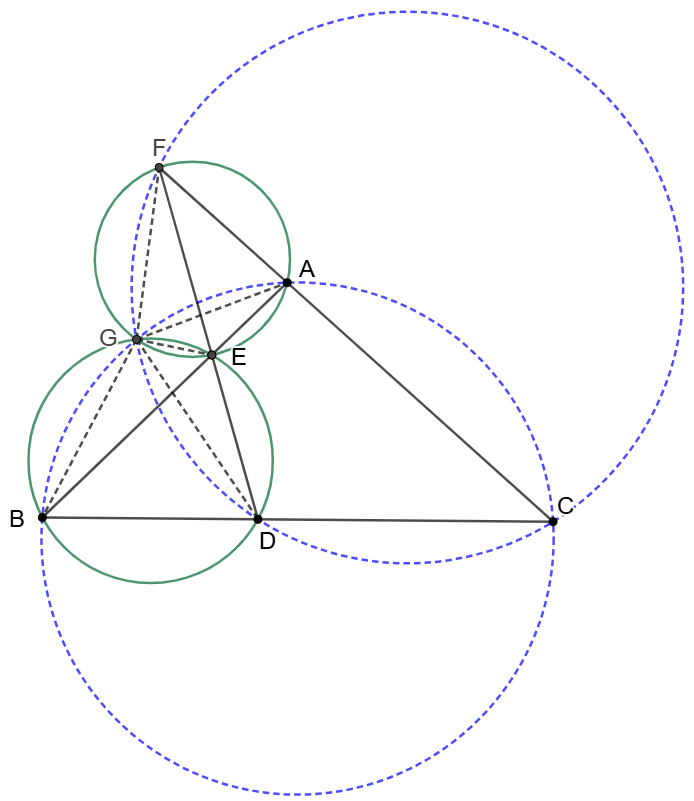
\shoveleft \text{We prove some lemma here: }\\
\shoveleft \text{if }\triangle{ABC}, \triangle{CDF} \text{ form a complete quadrilateral:}\\
\shoveleft D, E \text{ are two points on side }BC, AB \text{ of }\triangle{ABC}\\
\shoveleft DE\cap CA=F, \{E,G\}=(AEF)\cap(BDE)\\
\shoveleft \implies G \text{ is on }(ABC) \text{ and on }(CDF)\\
\shoveleft \text{This can be easily proved: }\\
\shoveleft \angle{CBG}=\angle{FEG}=\angle{FAG} \implies ABCG \text{ is cyclic}\\
\shoveleft \angle{CFG}=\angle{BEG}=\angle{BDG} \implies CDGF \text{ is cyclic} \blacksquare\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{We prove some lemma here: }\\
\shoveleft \text{if }\triangle{ABC}, \triangle{CDF} \text{ form a complete quadrilateral:}\\
\shoveleft D, E \text{ are two points on side }BC, AB \text{ of }\triangle{ABC}\\
\shoveleft DE\cap CA=F, \{E,G\}=(AEF)\cap(BDE)\\
\shoveleft \implies G \text{ is on }(ABC) \text{ and on }(CDF)\\
\shoveleft \text{This can be easily proved: }\\
\shoveleft \angle{CBG}=\angle{FEG}=\angle{FAG} \implies ABCG \text{ is cyclic}\\
\shoveleft \angle{CFG}=\angle{BEG}=\angle{BDG} \implies CDGF \text{ is cyclic} \blacksquare\\
\end{multline}\)
 \(\begin{multline}
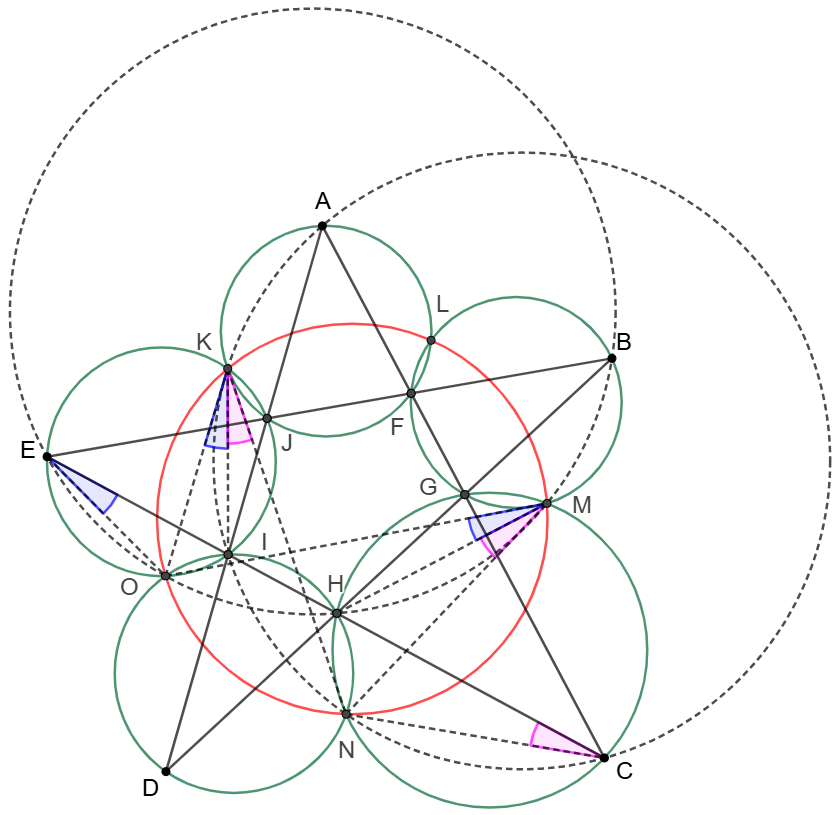
\shoveleft \text{Apply this lemma to the pentagram:}\\
\shoveleft K,N \text{ are on }(ACI) \implies \angle{IKN}=\angle{ICN}=\angle{HMN}\\
\shoveleft M,O \text{ are on }(BEH) \implies \angle{HMO}=\angle{HEO}=\angle{IKO}\\
\shoveleft \implies \angle{OKM}=\angle{IKO}+\angle{IKN}=\angle{HMN}+\angle{HMO}=\angle{OMN}\\
\shoveleft \implies MNOK \text{ is cyclic} \\
\shoveleft \text{Similarly }LMOK \text{ is cyclic}\implies KLMNO \text{ is cyclic}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Apply this lemma to the pentagram:}\\
\shoveleft K,N \text{ are on }(ACI) \implies \angle{IKN}=\angle{ICN}=\angle{HMN}\\
\shoveleft M,O \text{ are on }(BEH) \implies \angle{HMO}=\angle{HEO}=\angle{IKO}\\
\shoveleft \implies \angle{OKM}=\angle{IKO}+\angle{IKN}=\angle{HMN}+\angle{HMO}=\angle{OMN}\\
\shoveleft \implies MNOK \text{ is cyclic} \\
\shoveleft \text{Similarly }LMOK \text{ is cyclic}\implies KLMNO \text{ is cyclic}\blacksquare
\end{multline}\)
Prove 2:
 \(\begin{multline}
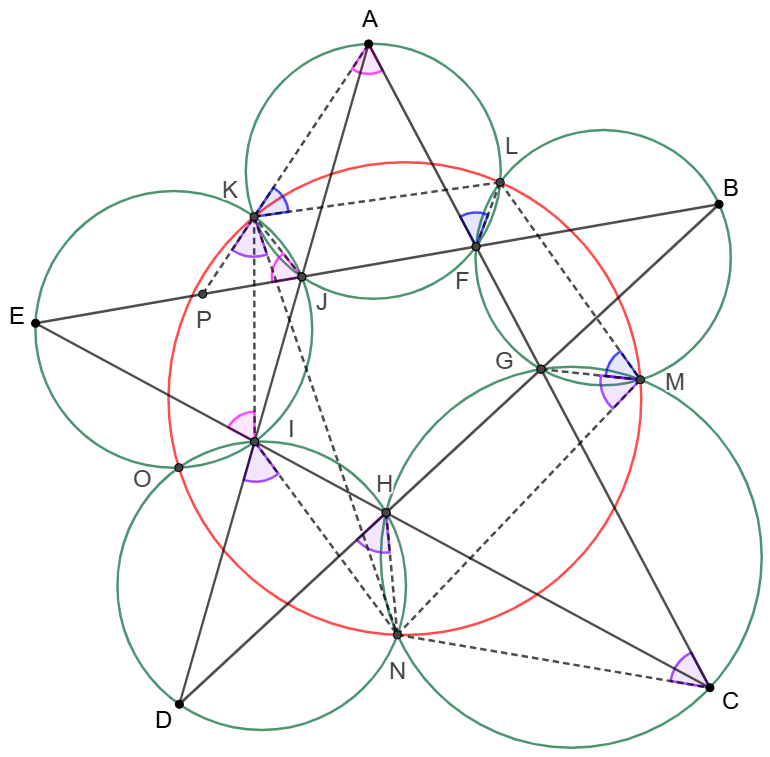
\shoveleft \angle{FAK}=\angle{EJK}=\angle{EIK}\implies ACIK \text{ is cyclic}\\
\shoveleft \angle{ACN}=\angle{DHN}=\angle{DIN}\implies ACNI \text{ is cyclic}\\
\shoveleft \implies ACINK \text{ is cyclic}\implies ACNK \text{ is cyclic}\\
\shoveleft \text{Let }AK\cap BE=P \implies \angle{PKN}=\angle{ACN}\\
\shoveleft \implies 180^{\circ}-\angle{LKN}=\angle{AKL}+\angle{PKN}\\
\shoveleft =\angle{AFL}+\angle{ACN}=\angle{GML}+\angle{GMN}\\
\shoveleft =\angle{LMN}\implies \angle{LMN}+\angle{LKN}=180^{\circ}\\
\shoveleft \implies KLMN \text{ is cyclic} \\
\shoveleft \text{Similarly }LMNO \text{ is cyclic}\implies KLMNO \text{ is cyclic}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \angle{FAK}=\angle{EJK}=\angle{EIK}\implies ACIK \text{ is cyclic}\\
\shoveleft \angle{ACN}=\angle{DHN}=\angle{DIN}\implies ACNI \text{ is cyclic}\\
\shoveleft \implies ACINK \text{ is cyclic}\implies ACNK \text{ is cyclic}\\
\shoveleft \text{Let }AK\cap BE=P \implies \angle{PKN}=\angle{ACN}\\
\shoveleft \implies 180^{\circ}-\angle{LKN}=\angle{AKL}+\angle{PKN}\\
\shoveleft =\angle{AFL}+\angle{ACN}=\angle{GML}+\angle{GMN}\\
\shoveleft =\angle{LMN}\implies \angle{LMN}+\angle{LKN}=180^{\circ}\\
\shoveleft \implies KLMN \text{ is cyclic} \\
\shoveleft \text{Similarly }LMNO \text{ is cyclic}\implies KLMNO \text{ is cyclic}\blacksquare
\end{multline}\)
12/03/2025
There are 10 multiple choice questions as following, find their answers.
-
Q1: the answer to Q1 is: $ (A) A \qquad (B) B \qquad (C) C \qquad (D) D$
-
Q2: The answer to Q5 is: $ (A) C \qquad (B) D \qquad (C) A \qquad (D) B $
-
Q3: Which question has a different answer to the other three: $ (A) Q3 \qquad (B) Q6 \qquad (C) Q2 \qquad (D) Q4 $
-
Q4: Which two questions have the same answer: $ (A) \text{Q1 and Q5} \qquad (B) \text{Q2 and Q7} \qquad (C) \text{Q1 and Q9} \qquad (D) \text{Q6 and Q10} $
-
Q5: Which question has the same answer as Q5: $(A) Q8 \qquad (B) Q4 \qquad (C) Q9 \qquad (D) Q7 $
-
Q6: which two questions have the same answer as Q8: $(A) \text{Q2 and Q4} \qquad (B) \text{Q1 and Q6} \qquad (C) \text{Q3 and Q10} \qquad (D) \text{Q5 and Q9} $
-
Q7: Which letter appears least in the answers of 10 questions: $ (A) C \qquad (B) B \qquad (C) A \qquad (D) D $
-
Q8: Which question has its answer letter that is not adjacent to that of Q1 in alphabet table: $(A) Q7 \qquad (B) Q5 \qquad (C) Q2 \qquad (D) Q10 $
-
Q9: Statement “Q1 and Q6 have the same answer” and “QX and Q5 have the same answer” are not true or false at same time. Then X is: $(A) 6 \qquad (B) 10 \qquad (C) 2 \qquad (D) 9 $
-
Q10: In the answers to the 10 questions, the difference between the number of times the letters ABCD appear most and least frequently is: $(A) 3 \qquad (B) 2 \qquad (C) 4 \qquad (D) 1 $
Solve:
\[\begin{multline} \shoveleft \text{Q3 implies that three of the four questions must have the same answer,}\\ \shoveleft \text{otherwise Q4 must have more than one answers which would bring mess to the logic.}\\ \shoveleft \text{Do the casework of Q3:}\\ \shoveleft \text{(1) Q2 has a different answer, and }Q3=Q4=Q6=C\\ \shoveleft \implies Q1=Q9,Q2 \ne C, Q3=Q8=Q10=Q4=Q6=C, \text{ do case work on Q1, Q9:}\\ \shoveleft \text{I: }Q1=Q9=A \implies Q1\ne Q6 \implies Q5=Q6=C \implies Q9=Q5 \color{red}{\Large\unicode{x2613}} \\ \shoveleft \text{II: }Q1=Q9=B \implies Q1\ne Q6 \implies Q5=Q6=C \implies Q9=Q5 \color{red}{\Large\unicode{x2613}} \\ \shoveleft \text{III: }Q1=Q9=C \implies Q2=Q5=C \color{red}{\Large\unicode{x2613}} \\ \shoveleft \text{IV: }Q1=Q9=D \implies Q1\ne Q6 \implies Q5=Q6=C \implies Q9=Q5 \color{red}{\Large\unicode{x2613}} \\ \shoveleft \implies (1) \color{red}{\Large\unicode{x2613}}\\ \shoveleft \text{(2) Q4 has a different answer, and }Q2=Q3=Q6=D\\ \shoveleft \implies Q5=B=Q8=Q9\implies Q5=A \text{ and }Q5=C \color{red}{\Large\unicode{x2613}}\\ \shoveleft \text{(3) Q6 has a different answer, and }Q2=Q3=Q4=B\\ \shoveleft \implies Q5=D, Q7=B \text{ and }Q5=Q7 \color{red}{\Large\unicode{x2613}}\\ \shoveleft \text{(4) Q3 has a different answer, Q3=A and }Q2=Q4=Q6, \text{ do casework here:}\\ \shoveleft \text{I: Q2=Q4=Q6=B} \implies Q7=B, Q5=D \implies Q5=Q7 \color{red}{\Large\unicode{x2613}}\\ \shoveleft \text{II: Q2=Q4=Q6=C} \implies Q5=A=Q8=Q10, Q1=Q9=B, Q7=D \implies \text{this answer works}\\ \shoveleft \text{III: Q2=Q4=Q6=D} \implies Q5=B=Q8=Q9,Q6=Q10=D \implies Q5 \ne Q6 \implies Q10=Q5 \color{red}{\Large\unicode{x2613}}\\ \shoveleft \implies \text{The answer is: }\bbox[5px, border: 1px solid black]{Q1=Q9=B, Q2=Q4=Q6=C, Q3=Q5=Q8=Q10=A, Q7=D} \end{multline}\]