11/01/2025

The diameter $AC$ and $BD$ of two semi-circles is tangent to the other semi-circle at mean time. Prove that $AB \parallel CD$.

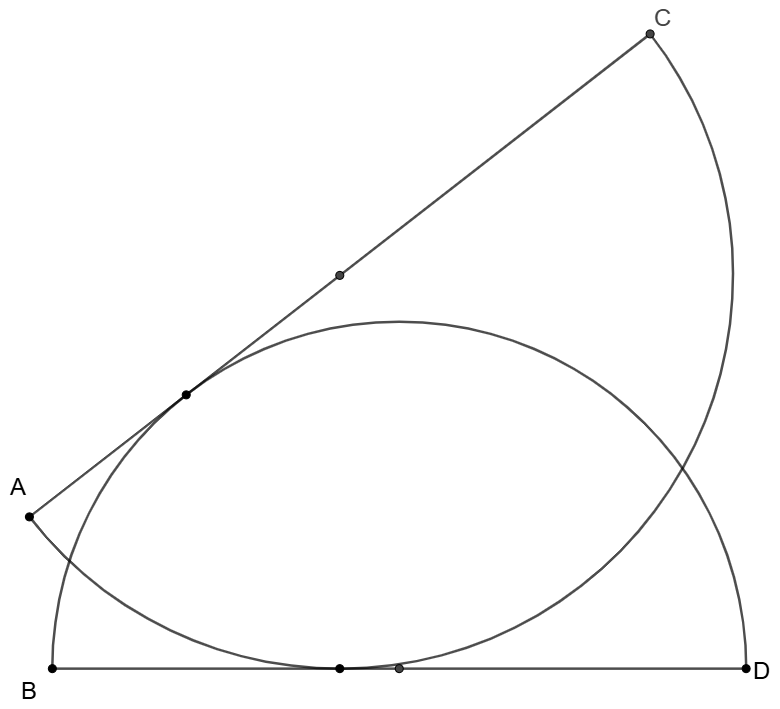
Prove:

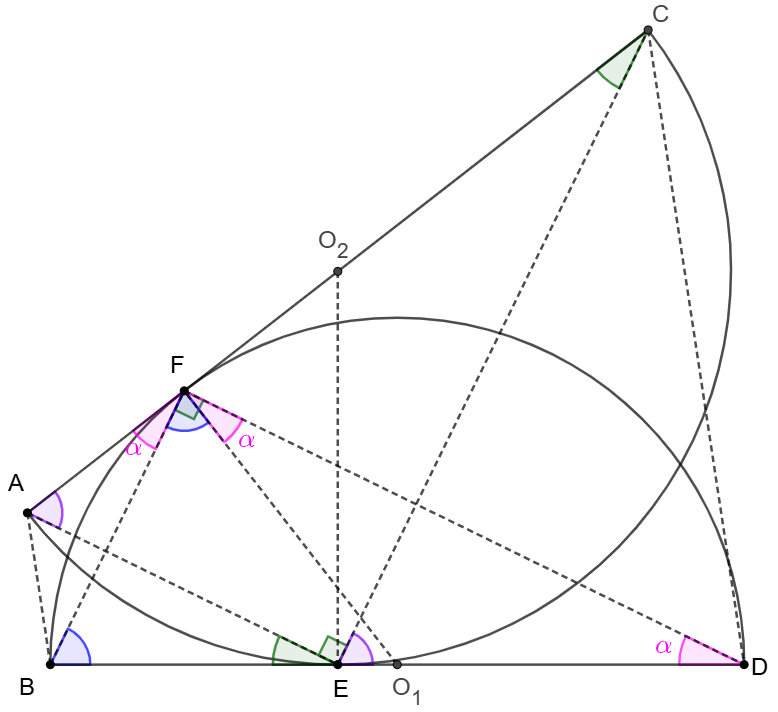\(\begin{multline} \shoveleft \text{Let }O_1, O_2 \text{ be the center of semi-circle }BD \text{ and }AC \text{ respectively}\\ \shoveleft \text{And }E, F\text{ are the tangent point on diameter }BD, AC \text{ respectively} \implies \\ \shoveleft O_1F\perp AC, O_2E\perp BD\implies O_1EFO_2\text{ are cyclic} \implies \angle{BO_1F}=\angle{AO_2E}\\ \shoveleft BO_1=FO_1, AO_2=EO_2 \implies \angle{O_1BF}=90^{\circ}-\dfrac{BO_1F}{2}=90^{\circ}-\dfrac{AO_2E}{2}=\angle{EAO_2}\\ \shoveleft \implies EBAF\text{ are cyclic} \implies \angle{AFB}=\angle{AEB}\implies \angle{ACE}=\angle{BDF}\\ \shoveleft \implies DEFC \text{ are cyclic} \implies \angle{FCD}=\angle{BEF}=180^{\circ}-\angle{BAF}\implies AB\parallel CD \blacksquare \end{multline}\)

---

11/14/2025

$A=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{308}+\frac{1}{309}$, $B=\frac{308}{1}+\frac{307}{2}+\frac{306}{3}+…+\frac{3}{306}+\frac{2}{307}+\frac{1}{308}$, find $\frac{A}{B}$

solve: \(\begin{multline} \shoveleft B+308=309(\frac{1}{1}+\dfrac{1}{2}+...+\frac{1}{308}) \implies B=309\sum_{i=1}^{308}{\frac{1}{i}}-308\\ \shoveleft A=\sum_{i=1}^{308}{\frac{1}{i}}-1+\frac{1}{309}=\sum_{i=1}^{308}{\frac{1}{i}}-\dfrac{308}{309} \implies \dfrac{A}{B}=\bbox[5px, border: 1px solid black]{\dfrac{1}{309}}\\ \shoveleft \end{multline}\)

---

11/18/2025

$F$ is a point on diagonal $AC$ of quadrilateral $ABCD$ such that $\angle{ABF}=60^{\circ}$, $\angle{FBC}=\angle{FCB}=16^{\circ}$, $\angle{ACD}=30^{\circ}$, $E$ is a point on side $BC$ such that $\angle{FED}=67^{\circ}$, $\angle{CED}=21^{\circ}$, find $\angle{CAD}$

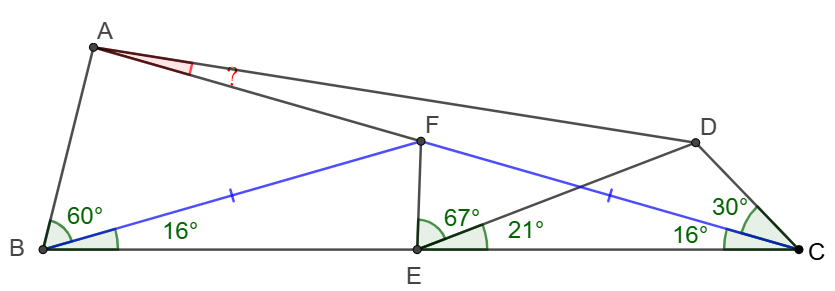
Solve:

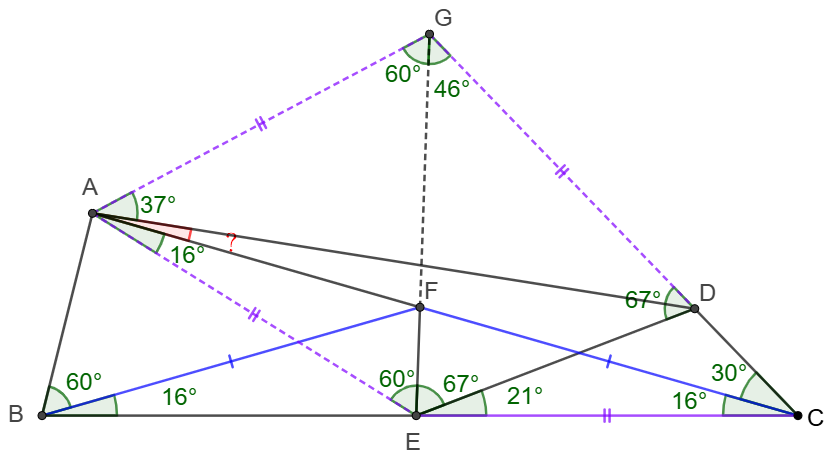\(\begin{multline} \shoveleft \angle{BAC}=88^{\circ}=\angle{CEF}\implies ABEF \text{ is cyclic} \implies \\ \shoveleft \angle{EAF}=\angle{EBF}=16^{\circ}=\angle{BCF}\implies AE=CE\\ \shoveleft \text{Extend }EF, CD \text{ and meet at }G \implies \angle{CGE}=46^{\circ}\\ \shoveleft \implies \angle{EDG}=67^{\circ}, \angle{ECG}=\angle{EGC} \implies\\ \shoveleft CE=EG=AE \implies EG=DG, \triangle{AEG}\text{ is equilateral}\\ \shoveleft \implies \angle{AGE}=\angle{EAG}=60^{\circ}, AG=EG=DG\\ \shoveleft \implies \angle{DAG}=\dfrac{180^{\circ}-106^{\circ}}{2}=37^{\circ}\implies\\ \shoveleft \angle{CAD}=60^{\circ}-16^{\circ}-37^{\circ}=\bbox[5px, border: 1px solid black]{7^{\circ}} \end{multline}\)

---