10/09/2025
$N$ is on side $BC$ of $\triangle{ABC}$, if $\dfrac{AB}{BN}=\dfrac{AC}{CN}$ show that $AN$ bisects $\angle{BAC}$
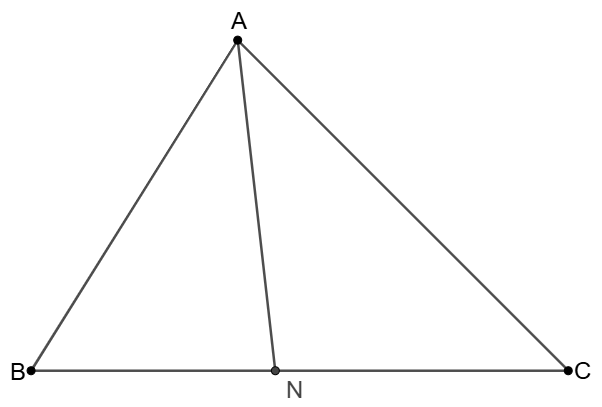
Prove:
\(\begin{multline}
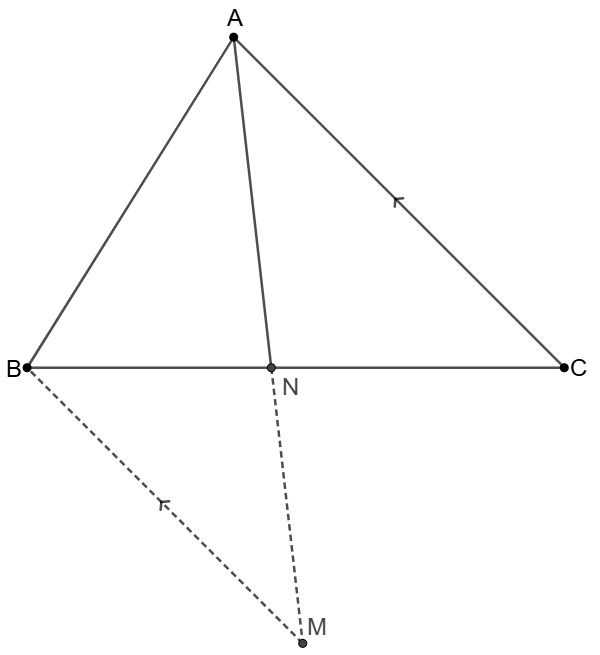
\shoveleft \text{Let }M \text{ on extended }AN \text{ and }BM\parallel AC\\
\shoveleft \implies \angle{NAC}=\angle{BMA}, \triangle{ANC}\sim\triangle{MNB}\\
\shoveleft\implies \dfrac{AC}{CN}=\dfrac{BM}{BN}=\dfrac{AB}{BN}\implies AB=BM\\
\shoveleft \implies \angle{BAN}=\angle{BMA}=\angle{NAC}\implies AN\text{ bisects }\angle{BAC}\blacksquare
\end{multline}\)
10/10/2025
$M, N$ are on extended side $CA, CB$ of $\triangle{ABC}$ respectively and $\dfrac{AB}{AC}=\dfrac{NB}{NC}$, show that $\angle{MAN}=\angle{NAB}$
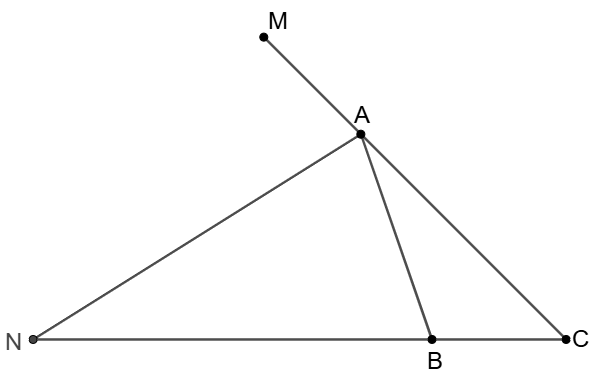
Prove:
\(\begin{multline}
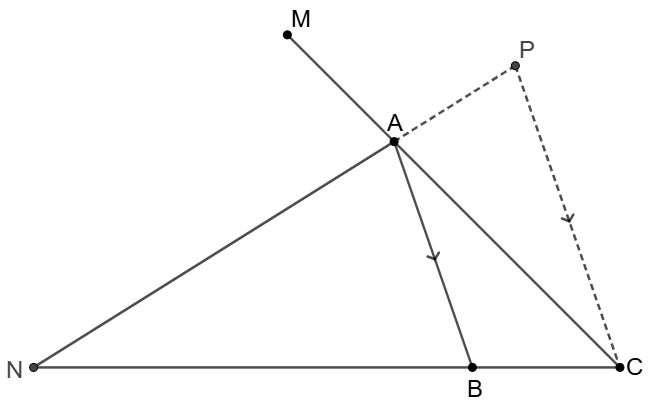
\shoveleft \text{Let }P \text{ on extended }NA \text{ and }PC\parallel AB \\
\shoveleft \implies \angle{NAB}=\angle{NPC}, \triangle{NAB}\sim\triangle{NPC}\\
\shoveleft \implies \dfrac{NB}{NC}=\dfrac{AB}{PC}=\dfrac{AB}{AC}\implies AC=PC\\
\shoveleft \implies \angle{APC}=\angle{PAC}=\angle{MAN}=\angle{NAB}\blacksquare
\end{multline}\)
10/23/2025
$\triangle{ACD}$ and $\triangle{BCE}$ are equilateral, show that $[ADBE]=\dfrac{\sqrt{3}}{4}AB^2$
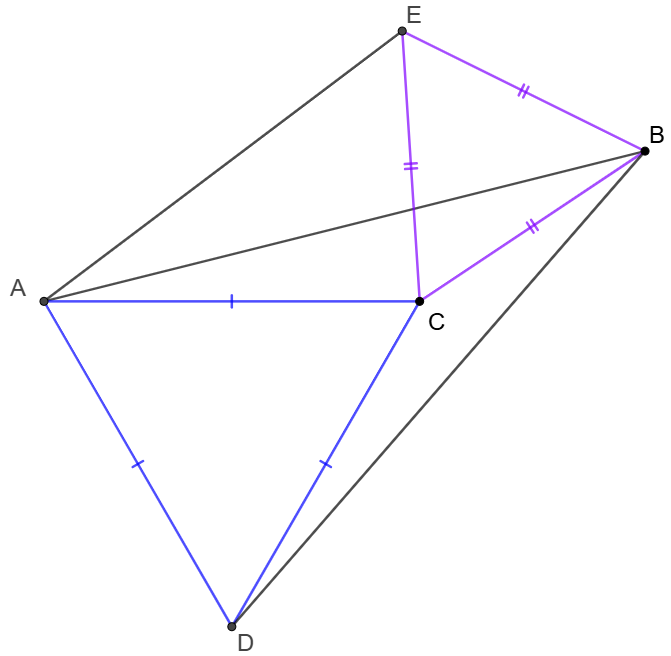
Prove 1: \(\begin{multline} \shoveleft \text{Let }AC=a, BC=b,\angle{ACE}=\theta\\ \shoveleft \implies AB^2=a^2+b^2-2abcos(\theta+60^{\circ})\\ \shoveleft =a^2+b^2+ab(\sqrt{3}sin\theta-cos\theta)\\ \shoveleft [ADBE]=[ACD]+[BCE]+[ACE]+[BCD]\\ \shoveleft [ADBE]=\dfrac{\sqrt{3}(a^2+b^2)}{4}+\dfrac{absin(240^{\circ}-\theta)}{2}+\dfrac{absin{\theta}}{2}\\ \shoveleft =\dfrac{\sqrt{3}}{4}[a^2+b^2+\dfrac{2ab}{\sqrt{3}}(-\dfrac{\sqrt{3}}{2}cos\theta+\dfrac{1}{2}sin\theta+sin\theta)]\\ \shoveleft =\dfrac{\sqrt{3}}{4}[a^2+b^2+ab(\sqrt{3}sin\theta-cos\theta)]=\dfrac{\sqrt{3}}{4}AB^2\blacksquare\\ \end{multline}\) Prove 2:
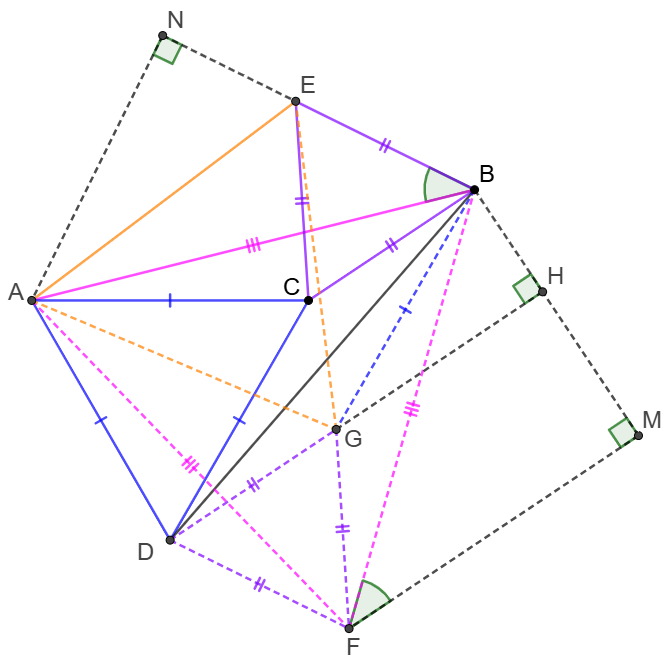\(\begin{multline}
\shoveleft \text{Rotate }\triangle{ABE} \text{ around }A \text{ for }60^{\circ} \text{ to get }\triangle{AFG}\\
\shoveleft \implies \triangle{AEG}, \triangle{ABF} \text{ are equilateral}, \triangle{ABE}\cong\triangle{AFG}\\
\shoveleft \implies \angle{ABE}=\angle{AFG}\implies \angle{ABC}=60^{\circ}-\angle{ABE}\\
\shoveleft =60^{\circ}-\angle{AFG}=\angle{BFG}=\angle{AFD}\\
\shoveleft BC=BE=FG=DF,AB=BF=AF\\
\shoveleft \implies \triangle{ABC}\cong\triangle{BFG}\cong\triangle{AFD}\\
\shoveleft CD=BG, BC=DG \implies \triangle{BCD}\cong\triangle{DGB}\\
\shoveleft \text{Make }AN\perp BE \text{ and }AN\cap BE=N\\
\shoveleft DG\perp BM, FM\perp BM \text{ and }DG\cap BM=H, FM \cap BM=M\\
\shoveleft \implies DG\parallel FM\implies \angle{GFM}=\angle{DGF}=60^{\circ}\\
\shoveleft \implies \angle{BFM}=60^{\circ}-\angle{BFG}=60^{\circ}-\angle{ABC}=\angle{ABN}\\
\shoveleft AB=BF\implies \triangle{ABN}\cong\triangle{BFM}\implies AN=BM\\
\shoveleft \implies AN=BH+HM\implies [ABE]=[BDG]+[DFG]\\
\shoveleft \implies [ADBE]=[ABE]+[ADF]+[AFG]+[ABG]-[DFG]-[BDG]\\
\shoveleft =[BDG]+[DFG]+[ADF]+[AFG]+[ABG]-[DFG]-[BDG]\\
\shoveleft =[ADF]+[AFG]+[ABG]=[BFG]+[AFG]+[ABG]=[ABF]\blacksquare
\end{multline}\)