09/05/2025

$D$ is on side $BC$ of $\triangle{ABC}$ such that $BD=2$, $CD=1$, $\angle{ADB}=60^{\circ}$, $\angle{ACB}=30^{\circ}$, find $\angle{ABC}$.

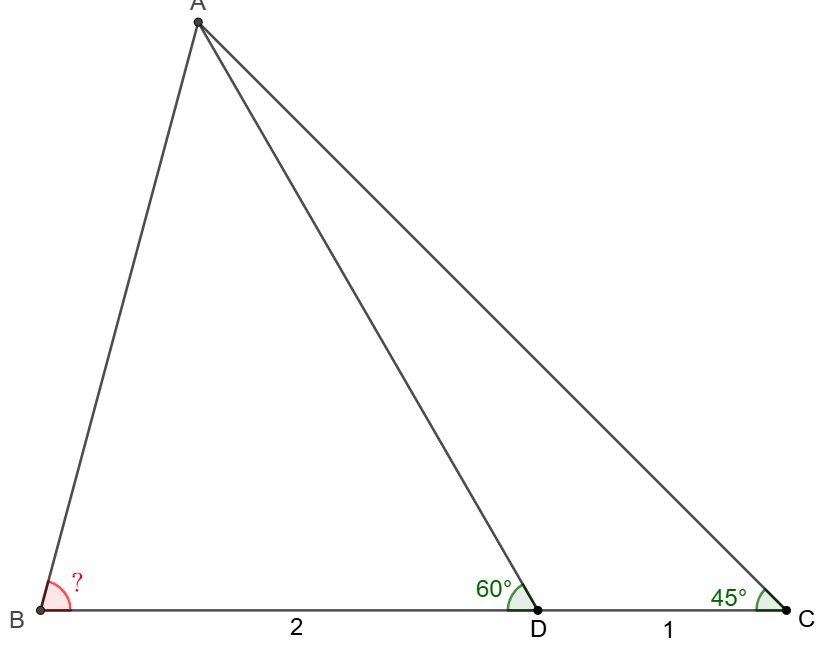
Solve:

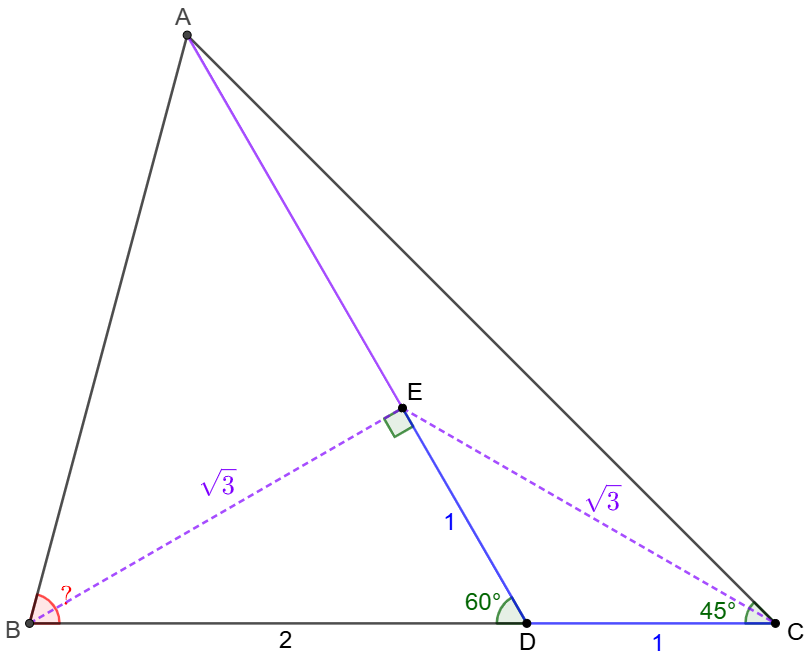\(\begin{multline} \shoveleft \text{Let } E \text{ on }AD \text{ such that }CD=DE \\ \shoveleft \implies BE=CE=\sqrt{3}, BE\perp DE\\ \shoveleft \implies \angle{CBE}=\angle{BCE}=30^{\circ}=\angle{CED}\\ \shoveleft \implies \angle{ACE}=45^{\circ}-30^{\circ}=15^{\circ}\\ \shoveleft \implies \angle{ACE}=15^{\circ}\implies CE=AE=BE\\ \shoveleft \implies \angle{ABE}=\angle{BAE}=45^{\circ}\\ \shoveleft \implies \angle{ABC}=\bbox[5px, border: 1px solid black]{75^{\circ}} \end{multline}\)

---

09/10/2025

In $\triangle{ABC}$, $CD\perp AB$, $\angle{BCD}=30^{\circ}$, $E$ is on $CD$ such that $\angle{CAE}=\angle{DAE}=10^{\circ}$, find $\angle{CBE}$.

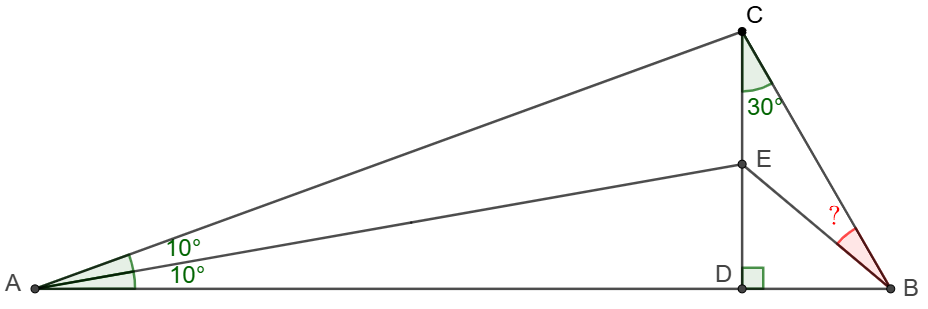
Solve:

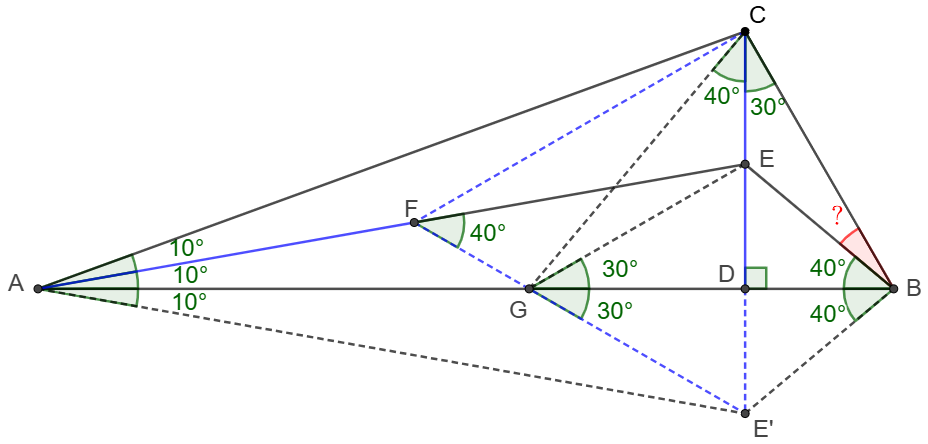\(\begin{multline} \shoveleft \text{Let }E' \text{ be the reflection of }E \text{ along }AB \implies \angle{E'AD}=\angle{DAE}=10^{\circ}\\ \shoveleft \text{Let }F \text{ be the circumcenter of }\triangle{CAE'} \implies \angle{CFE'}=2\angle{CAE'}=60^{\circ} \\ \shoveleft \implies \triangle{CE'F} \text{ is equilateral }\implies AF=CF=E'F=CE'\\ \shoveleft \angle{CFE'}=60^{\circ} \implies \angle{FE'A}=20^{\circ}=\angle{FAE'} \implies F \text{ is on }AE\\ \shoveleft \text{Let }E'F\cap AD=G, \angle{E'GD}=30^{\circ}=\angle{EGD}=\angle{BCD} \\ \shoveleft \implies BCGE' \text{ is cyclic}, \angle{EGE'}=60^{\circ}=\angle{E'CF}\implies ECFG\text{ is cyclic}\\ \shoveleft \implies \angle{EFG}=40^{\circ}=\angle{ECG}=\angle{E'BG}=\angle{EBG}\\ \shoveleft \implies \angle{CBE}=\angle{CBD}-\angle{EBD}=60^{\circ}-40^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}}\\ \end{multline}\)

---

09/21/2025

$AD, BE$ are two latitudes of $\triangle{ABC}$, $\angle{ABE}=30^{\circ}$, $AD\cap BE=F$, $AF=8$, find the radius of the circumcircle of $\triangle{ABC}$.

Solve:

\(\begin{multline} \shoveleft \text{Let }O \text{ be the circumcenter of } \triangle{ABC} \implies AO=BO=CO\\ \shoveleft \angle{ABE}=30^{\circ} \implies \angle{BAC}=60^{\circ}\implies \angle{BOC}=120^{\circ} \implies \angle{OBC}=30^{\circ}\\ \shoveleft \text{Let }OG\perp AB, OG\cap BE=H \implies OG \text{ is perpendicular bisector of }AB\\ \shoveleft \implies \angle{HBO}=\angle{HAO}, \angle{BAH}=\angle{ABH}=30^{\circ} \implies \angle{CAH}=30^{\circ}\\ \shoveleft AD\perp BC, BE\perp AC \implies \angle{DAE}=\angle{BDE}\implies 30^{\circ}+\angle{HBO}=30^{\circ}+\angle{FAH}\\ \shoveleft \implies \angle{HBO}=\angle{FAH}=\angle{HAO}, \angle{AHF}=120^{\circ}=\angle{AHO}\implies \triangle{AFH}\cong\triangle{AOH}\\ \shoveleft \implies AO=BO=CO=AF=R=\bbox[5px, border: 1px solid black]{8} \end{multline}\)