08/13/2025
$\triangle{ABC}$ is inscribed in a circle and the tangent lines at $A,B$ meet at $M$, the tangent lines at $B,C$ meet at $N$. $BP\perp AC$ at $P$, show that $\angle{MPB}=\angle{NPB}$.
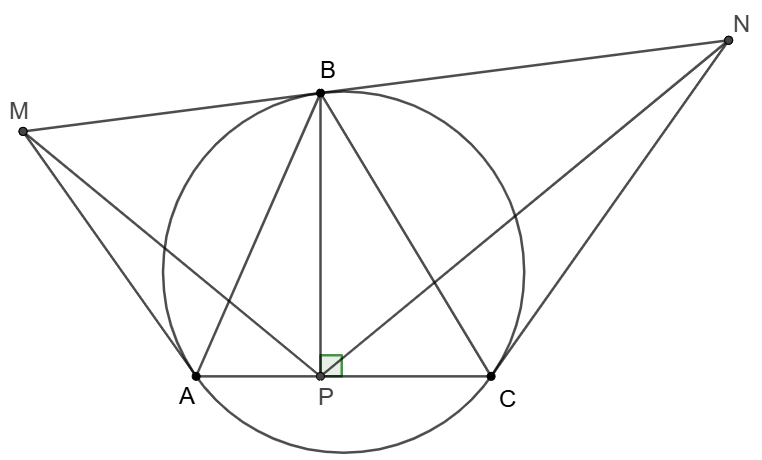
Prove 1:
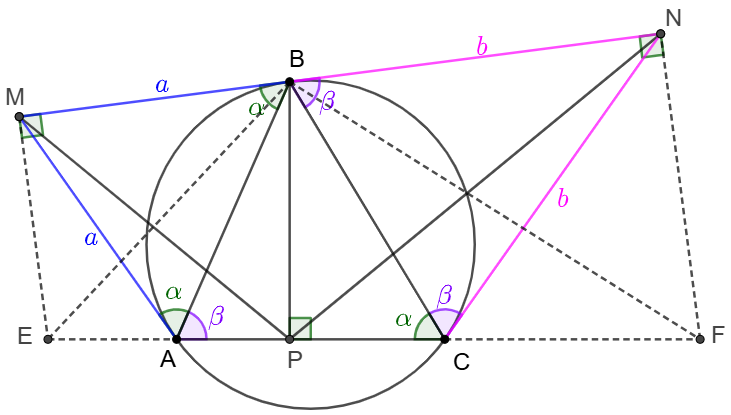 \(\begin{multline}
\shoveleft \text{Let }E, F \text{ on extended }AC \text{ such that }EM\perp MN, FN \perp MN\\
\shoveleft \implies EMBP, FNBP \text{ is both cyclic }\\
\shoveleft \implies \angle{MPB}=\angle{MEB}, \angle{NBP}=\angle{NFB}\\
\shoveleft \text{Let }MB=MA=a, NB=NC=b\\
\shoveleft \angle{MAB}=\angle{MBA}=\angle{BCA}=\alpha, \angle{NBC}=\angle{NCB}=\angle{BAC}=\beta\\
\shoveleft \implies sin\angle{AEM}=sin\angle{NBP}=sin\angle{NFC}\\
\shoveleft \implies \angle{MAE}=180^{\circ}-\alpha-\beta=\angle{NCF} \implies sin\angle{MAE}=sin\angle{NCF}\\
\shoveleft \implies \dfrac{ME}{MB}=\dfrac{ME}{MA}=\dfrac{sin\angle{MAE}}{sin\angle{AEM}}=\dfrac{sin\angle{NCF}}{sin\angle{NFC}}=\dfrac{NF}{NC}=\dfrac{NF}{NB}\\
\shoveleft \implies \triangle{EMB}\sim\triangle{FNB}\implies \angle{MEB}=\angle{NFB}\implies \angle{MPB}=\angle{NPB} \blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}
\shoveleft \text{Let }E, F \text{ on extended }AC \text{ such that }EM\perp MN, FN \perp MN\\
\shoveleft \implies EMBP, FNBP \text{ is both cyclic }\\
\shoveleft \implies \angle{MPB}=\angle{MEB}, \angle{NBP}=\angle{NFB}\\
\shoveleft \text{Let }MB=MA=a, NB=NC=b\\
\shoveleft \angle{MAB}=\angle{MBA}=\angle{BCA}=\alpha, \angle{NBC}=\angle{NCB}=\angle{BAC}=\beta\\
\shoveleft \implies sin\angle{AEM}=sin\angle{NBP}=sin\angle{NFC}\\
\shoveleft \implies \angle{MAE}=180^{\circ}-\alpha-\beta=\angle{NCF} \implies sin\angle{MAE}=sin\angle{NCF}\\
\shoveleft \implies \dfrac{ME}{MB}=\dfrac{ME}{MA}=\dfrac{sin\angle{MAE}}{sin\angle{AEM}}=\dfrac{sin\angle{NCF}}{sin\angle{NFC}}=\dfrac{NF}{NC}=\dfrac{NF}{NB}\\
\shoveleft \implies \triangle{EMB}\sim\triangle{FNB}\implies \angle{MEB}=\angle{NFB}\implies \angle{MPB}=\angle{NPB} \blacksquare
\end{multline}\)
Prove 2:
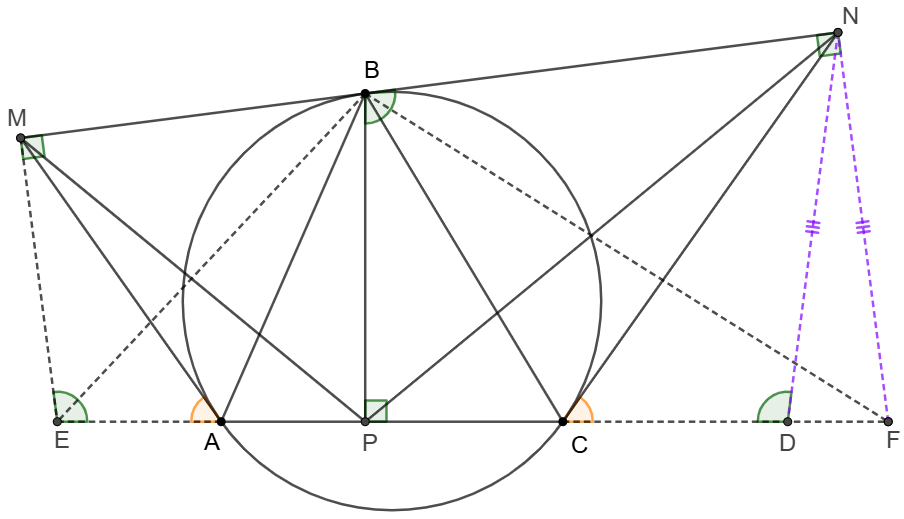 \(\begin{multline}
\shoveleft \text{Let }E, F \text{ on extended }AC \text{ such that }EM\perp MN, FN \perp MN\\
\shoveleft \implies EMBP, FNBP \text{ is both cyclic }\\
\shoveleft \implies \angle{MPB}=\angle{MEB}, \angle{NBP}=\angle{NFB}\\
\shoveleft \text{Let }D \text{ on }EF \text{ such that }ND=NF\implies \angle{CDN}=180^{\circ}-\angle{NFD}\\
\shoveleft \implies \angle{MEA}=\angle{NBP}=180^{\circ}-\angle{NFD}=\angle{CDN}\\
\shoveleft \angle{MAB}=\angle{MBA}=\angle{BCA}, \angle{NBC}=\angle{NCB}=\angle{BAC}\\
\shoveleft \implies \angle{MAE}=\angle{NCF} \implies \triangle{AEM}\sim\triangle{CDN}\\
\shoveleft \implies \dfrac{ME}{MA}=\dfrac{ND}{NC}\implies \dfrac{ME}{MB}=\dfrac{NF}{NB} \implies \triangle{EMB}\sim\triangle{FNB}\\
\shoveleft \implies \angle{MEB}=\angle{NFB} \implies \angle{MPB}=\angle{NPB} \blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E, F \text{ on extended }AC \text{ such that }EM\perp MN, FN \perp MN\\
\shoveleft \implies EMBP, FNBP \text{ is both cyclic }\\
\shoveleft \implies \angle{MPB}=\angle{MEB}, \angle{NBP}=\angle{NFB}\\
\shoveleft \text{Let }D \text{ on }EF \text{ such that }ND=NF\implies \angle{CDN}=180^{\circ}-\angle{NFD}\\
\shoveleft \implies \angle{MEA}=\angle{NBP}=180^{\circ}-\angle{NFD}=\angle{CDN}\\
\shoveleft \angle{MAB}=\angle{MBA}=\angle{BCA}, \angle{NBC}=\angle{NCB}=\angle{BAC}\\
\shoveleft \implies \angle{MAE}=\angle{NCF} \implies \triangle{AEM}\sim\triangle{CDN}\\
\shoveleft \implies \dfrac{ME}{MA}=\dfrac{ND}{NC}\implies \dfrac{ME}{MB}=\dfrac{NF}{NB} \implies \triangle{EMB}\sim\triangle{FNB}\\
\shoveleft \implies \angle{MEB}=\angle{NFB} \implies \angle{MPB}=\angle{NPB} \blacksquare
\end{multline}\)
Prove 3:
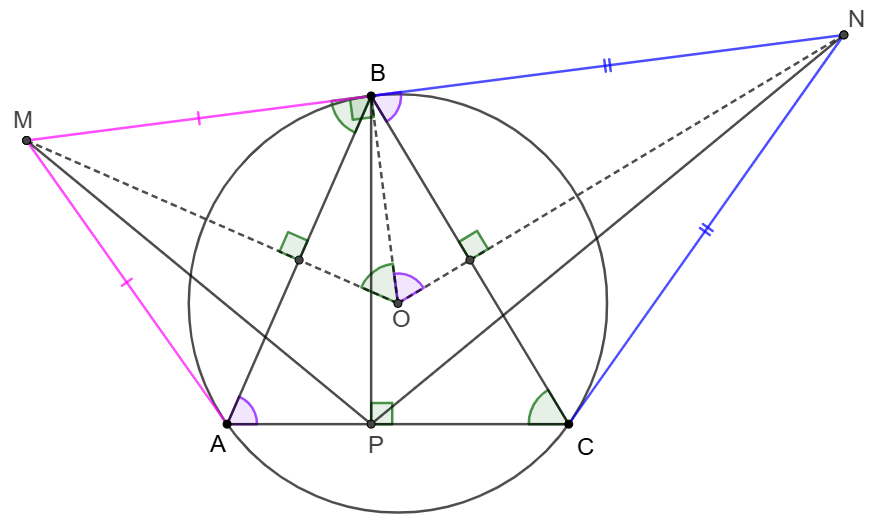 \(\begin{multline}
\shoveleft \text{Let }O \text{ be the center of the circumcircle of }\triangle{ABC}\\
\shoveleft \implies OB\perp MN, MO\perp AB, NO \perp BC\\
\shoveleft \implies \angle{ABM}=\angle{ACB}=\angle{MOB}, \angle{CAB}=\angle{CBN}=\angle{NOB}\\
\shoveleft \implies \triangle{BMO}\sim\triangle{PBC}, \triangle{BNO}\sim\triangle{PBA}\\
\shoveleft \implies \dfrac{MB}{BO}=\dfrac{BP}{PC},\dfrac{NB}{BO}=\dfrac{BP}{PA}\implies \dfrac{MB}{NB}=\dfrac{PA}{PC}=\dfrac{MA}{NC}\\
\shoveleft \angle{PAM}=\angle{PCN}\implies \triangle{MAP}\sim\triangle{NCP}\\
\shoveleft \implies \angle{MPA}=\angle{NPC} \implies \angle{MPB}=\angle{NPB}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }O \text{ be the center of the circumcircle of }\triangle{ABC}\\
\shoveleft \implies OB\perp MN, MO\perp AB, NO \perp BC\\
\shoveleft \implies \angle{ABM}=\angle{ACB}=\angle{MOB}, \angle{CAB}=\angle{CBN}=\angle{NOB}\\
\shoveleft \implies \triangle{BMO}\sim\triangle{PBC}, \triangle{BNO}\sim\triangle{PBA}\\
\shoveleft \implies \dfrac{MB}{BO}=\dfrac{BP}{PC},\dfrac{NB}{BO}=\dfrac{BP}{PA}\implies \dfrac{MB}{NB}=\dfrac{PA}{PC}=\dfrac{MA}{NC}\\
\shoveleft \angle{PAM}=\angle{PCN}\implies \triangle{MAP}\sim\triangle{NCP}\\
\shoveleft \implies \angle{MPA}=\angle{NPC} \implies \angle{MPB}=\angle{NPB}\blacksquare
\end{multline}\)
08/18/2025
$ABCD$ and $A’B’C’D’$ are both squares and $D’A’ \cap AB = E$, $A’B’\cap BC=F$,$B’C’ \cap CD = G$, $C’D’ \cap DA = H$. Show that $EG\perp FH$
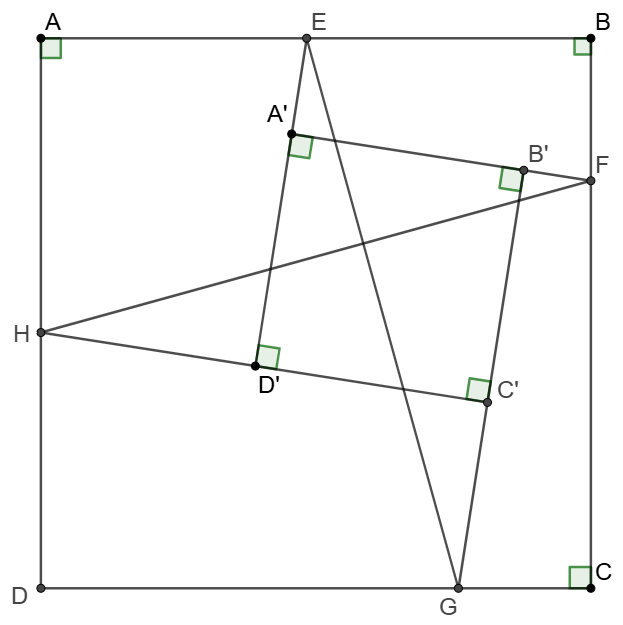
Prove:
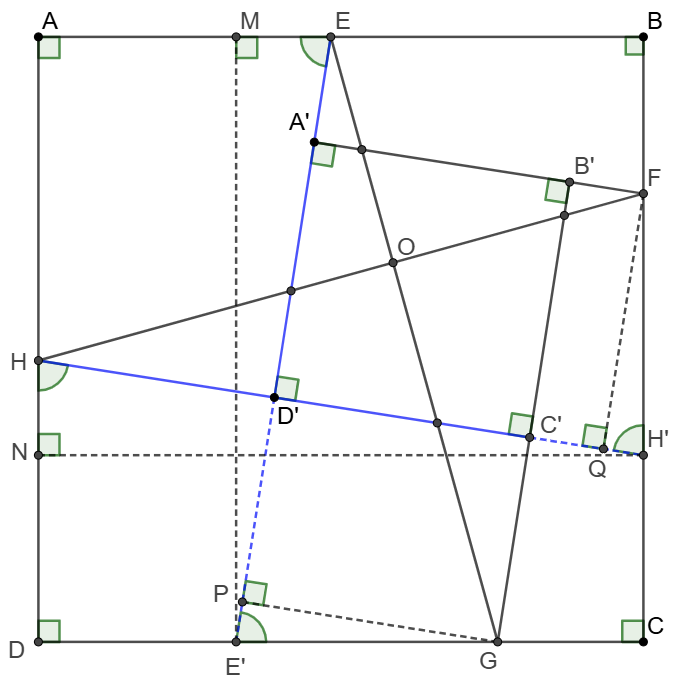 \(\begin{multline}
\shoveleft \text{Let }A'D'\cap CD = E', D'C' \cap BC=H', EG\cap FH=O\\
\shoveleft E'M \perp AB \text{ at } M, H'N' \perp DA \text{ at }N\\
\shoveleft GP \perp EE' \text{ at }P, FQ \perp HH' \text{ at }Q\\
\shoveleft AD\perp CD, D'H\perp D'E' \implies D'E'DH \text{ is cyclic }\\
\shoveleft \implies \angle{EE'G}=\angle{NHH'}=\angle{MEE'}=\angle{FH'H}\\
\shoveleft NH'=ME'=AB \implies \triangle{HNH'}\cong\triangle{EME'}\\
\shoveleft \implies EE'=HH'\\
\shoveleft PG=C'D'=B'C'=FQ \implies \triangle{PE'G}\cong\triangle{H'QF}\\
\shoveleft \implies E'G=H'F\implies \triangle{FHH'}\cong\triangle{E'EG}\\
\shoveleft \implies \angle{H'HF}=\angle{E'EG}\implies D'HEO \text{ is cyclic}\\
\shoveleft \implies \angle{EOH}=\angle{ED'H}=90^{\circ}\implies EG \perp FH \blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }A'D'\cap CD = E', D'C' \cap BC=H', EG\cap FH=O\\
\shoveleft E'M \perp AB \text{ at } M, H'N' \perp DA \text{ at }N\\
\shoveleft GP \perp EE' \text{ at }P, FQ \perp HH' \text{ at }Q\\
\shoveleft AD\perp CD, D'H\perp D'E' \implies D'E'DH \text{ is cyclic }\\
\shoveleft \implies \angle{EE'G}=\angle{NHH'}=\angle{MEE'}=\angle{FH'H}\\
\shoveleft NH'=ME'=AB \implies \triangle{HNH'}\cong\triangle{EME'}\\
\shoveleft \implies EE'=HH'\\
\shoveleft PG=C'D'=B'C'=FQ \implies \triangle{PE'G}\cong\triangle{H'QF}\\
\shoveleft \implies E'G=H'F\implies \triangle{FHH'}\cong\triangle{E'EG}\\
\shoveleft \implies \angle{H'HF}=\angle{E'EG}\implies D'HEO \text{ is cyclic}\\
\shoveleft \implies \angle{EOH}=\angle{ED'H}=90^{\circ}\implies EG \perp FH \blacksquare
\end{multline}\)
08/22/2025
Find the area of the square:
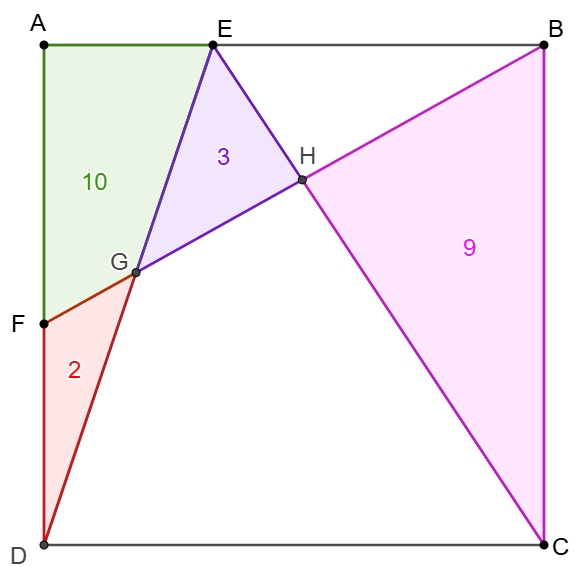
Solve:
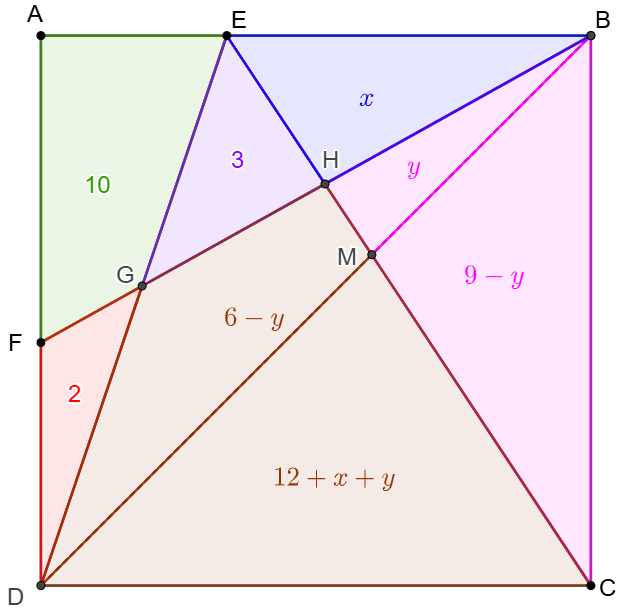 \(\begin{multline}
\shoveleft \text{Let }BD \cap CE=M, [BEH]=x,[BHM]=y\\
\shoveleft \implies [BCE]=[BDE]\implies [DGHM]=6-y\\
\shoveleft [BEC]+[ADE]=[CDE]\implies[CDGH]=18+x\\
\shoveleft \implies [CDM]=12+x+y\\
\shoveleft \text{Apply Cross Ladder Theorem on }\triangle{ABD} \implies\\
\shoveleft \dfrac{1}{[BDE]}+\dfrac{1}{[BDF]}=\dfrac{1}{[BDG]}+\dfrac{1}{[BDA]}\\
\shoveleft \implies \dfrac{1}{8}+\dfrac{1}{x+9}=\dfrac{1}{6}+\dfrac{1}{x+21} \implies x=3\\
\shoveleft \implies [ABCD]=2(21+x)=\bbox[5px, border: 1px solid black]{48}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }BD \cap CE=M, [BEH]=x,[BHM]=y\\
\shoveleft \implies [BCE]=[BDE]\implies [DGHM]=6-y\\
\shoveleft [BEC]+[ADE]=[CDE]\implies[CDGH]=18+x\\
\shoveleft \implies [CDM]=12+x+y\\
\shoveleft \text{Apply Cross Ladder Theorem on }\triangle{ABD} \implies\\
\shoveleft \dfrac{1}{[BDE]}+\dfrac{1}{[BDF]}=\dfrac{1}{[BDG]}+\dfrac{1}{[BDA]}\\
\shoveleft \implies \dfrac{1}{8}+\dfrac{1}{x+9}=\dfrac{1}{6}+\dfrac{1}{x+21} \implies x=3\\
\shoveleft \implies [ABCD]=2(21+x)=\bbox[5px, border: 1px solid black]{48}
\end{multline}\)
08/27/2025
$ABCD$ is a square and $E$ is inside it such that $CEGF$ form another square and $AE \parallel DG$. Show that $GD\perp DE$.
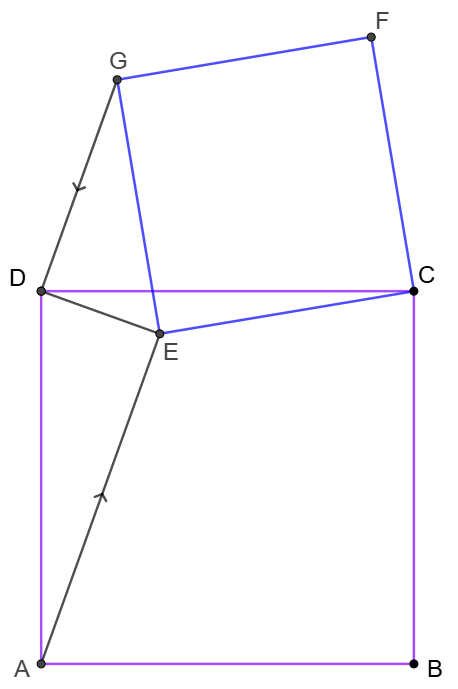
Prove:
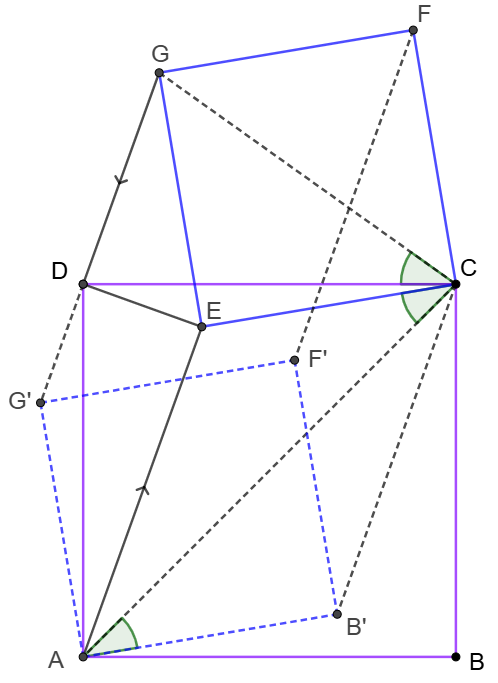 \(\begin{multline}
\shoveleft \text{Extend } DG \text{ to }G' \text{ such that }AEGG' \text{ form a parallelogram}\\
\shoveleft \text{Make }AB'F'G' \text{ to be a square} \implies AB'\parallel CE\implies \angle{ACE}=\angle{B'AC}\\
\shoveleft \angle{ACD}=\angle{ECG}=45^{\circ}\implies \angle{DCG}=\angle{ACE}=\angle{B'AC}\\
\shoveleft \implies \angle{DAG'}=90^{\circ}-45^{\circ}-\angle{B'AC}=90^{\circ}-45^{\circ}=\angle{DCG}=\angle{DCE}\\
\shoveleft AG'=CE, AD=CD\implies \triangle{ADG'}\cong\triangle{CDE}\implies \angle{ADG'}=\angle{CDE}\\
\shoveleft \implies \angle{CDE}+\angle{ADE}=90^{\circ}=\angle{ADG'}+\angle{ADE}=\angle{EDG'}\implies GD\perp DE \blacksquare\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Extend } DG \text{ to }G' \text{ such that }AEGG' \text{ form a parallelogram}\\
\shoveleft \text{Make }AB'F'G' \text{ to be a square} \implies AB'\parallel CE\implies \angle{ACE}=\angle{B'AC}\\
\shoveleft \angle{ACD}=\angle{ECG}=45^{\circ}\implies \angle{DCG}=\angle{ACE}=\angle{B'AC}\\
\shoveleft \implies \angle{DAG'}=90^{\circ}-45^{\circ}-\angle{B'AC}=90^{\circ}-45^{\circ}=\angle{DCG}=\angle{DCE}\\
\shoveleft AG'=CE, AD=CD\implies \triangle{ADG'}\cong\triangle{CDE}\implies \angle{ADG'}=\angle{CDE}\\
\shoveleft \implies \angle{CDE}+\angle{ADE}=90^{\circ}=\angle{ADG'}+\angle{ADE}=\angle{EDG'}\implies GD\perp DE \blacksquare\\
\end{multline}\)
test some code change