07/02/2025
$ABCD$ is a quadrilateral such that $AB \perp BC, AD \perp CD$. $r_1, r_2, r_3, r_4$ are radiuses of external inscribed circles as shown in following figure. Show that $r_1+r_2=r_3+r_4$.
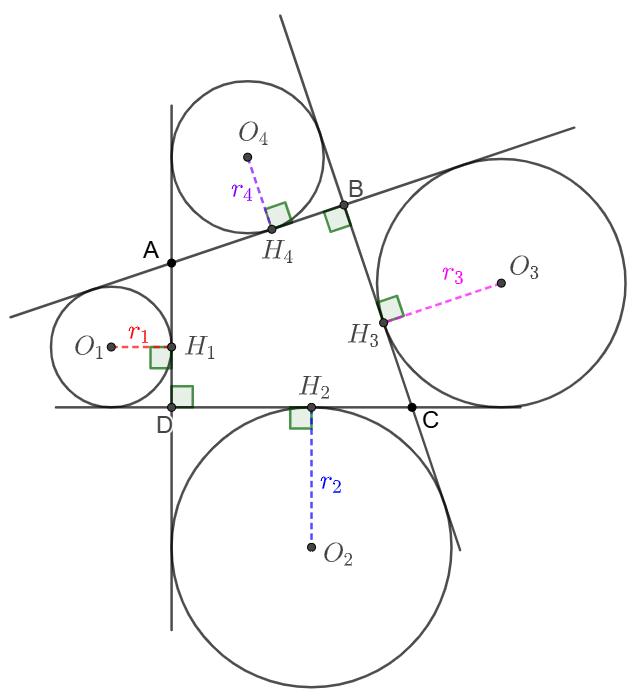
Prove:
 \(\begin{multline}
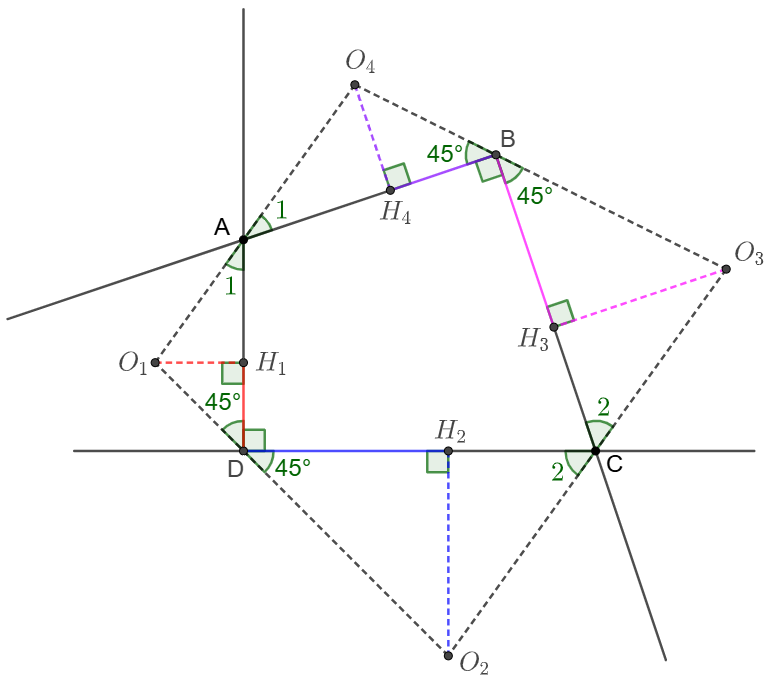
\shoveleft \text{Make }O_1H_1 \perp AD, O_2H_2 \perp CD, O_3H_3 \perp BC, O_4H_4 \perp AB\\
\shoveleft AD\perp CD, AB \perp BC \implies O_1H_1=H_1D=r_1\\
\shoveleft O_2H_2=DH_2=r_2, O_3H_3=BH_3=r_3, O_4H_4=BH_4=r_4\\
\shoveleft \angle{O_1AH_1}=\angle{O_4AH_4}, \angle{O_2CH_2}=\angle{O_3CH_3}\\
\shoveleft \angle{O_1DH_1}=\angle{O_2DH_2}=\angle{O_3BH_3}=\angle{O_4BH_4}=45^{\circ}\\
\shoveleft \implies \angle{O_2O_1O_4}=\angle{O_3O_4O_1}, \angle{O_3O_2O_1}=\angle{O_2O_3O_4}\\
\shoveleft \implies \angle{O_2O_1O_4}+\angle{O_3O_2O_1}=\dfrac{\angle{O_2O_1O_4}+\angle{O_1O_4O_3}+\angle{O_4O_3O_2}+\angle{O_3O_2O_1}}{2}\\
\shoveleft =180^{\circ}\implies O_2O_3 \parallel O_1O_4 \implies O_1O_2O_3O_4 \text{ is an isoceles trapezoid }\\
\shoveleft \implies O_1O_2=O_3O_4\implies \dfrac{O_1O_2}{\sqrt{2}}=\dfrac{O_3O_4}{\sqrt{2}}\implies r_1+r_2=r_3+r_4\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }O_1H_1 \perp AD, O_2H_2 \perp CD, O_3H_3 \perp BC, O_4H_4 \perp AB\\
\shoveleft AD\perp CD, AB \perp BC \implies O_1H_1=H_1D=r_1\\
\shoveleft O_2H_2=DH_2=r_2, O_3H_3=BH_3=r_3, O_4H_4=BH_4=r_4\\
\shoveleft \angle{O_1AH_1}=\angle{O_4AH_4}, \angle{O_2CH_2}=\angle{O_3CH_3}\\
\shoveleft \angle{O_1DH_1}=\angle{O_2DH_2}=\angle{O_3BH_3}=\angle{O_4BH_4}=45^{\circ}\\
\shoveleft \implies \angle{O_2O_1O_4}=\angle{O_3O_4O_1}, \angle{O_3O_2O_1}=\angle{O_2O_3O_4}\\
\shoveleft \implies \angle{O_2O_1O_4}+\angle{O_3O_2O_1}=\dfrac{\angle{O_2O_1O_4}+\angle{O_1O_4O_3}+\angle{O_4O_3O_2}+\angle{O_3O_2O_1}}{2}\\
\shoveleft =180^{\circ}\implies O_2O_3 \parallel O_1O_4 \implies O_1O_2O_3O_4 \text{ is an isoceles trapezoid }\\
\shoveleft \implies O_1O_2=O_3O_4\implies \dfrac{O_1O_2}{\sqrt{2}}=\dfrac{O_3O_4}{\sqrt{2}}\implies r_1+r_2=r_3+r_4\blacksquare
\end{multline}\)
07/07/2025
$D, E$ are two points on the base side $BC$ of isosceles triangle $\triangle{ABC}$ such that $AD=CD, BE=2DE$. $BF\perp AE$ at $F$. Prove $CF=AB$.
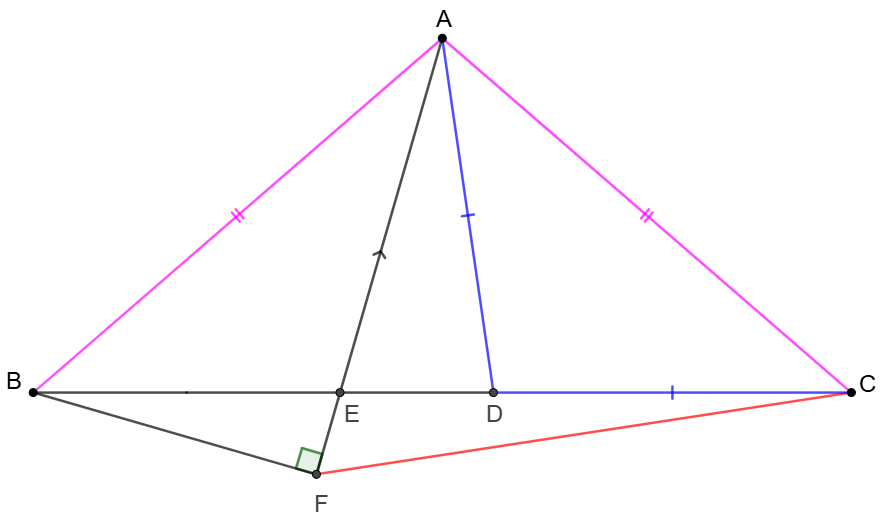
Prove 1:
 \(\begin{multline}
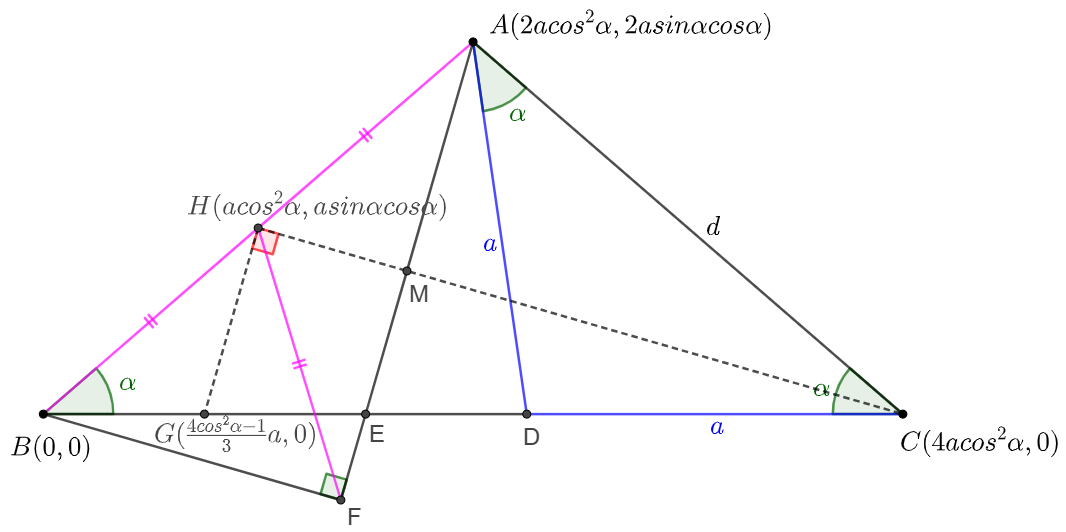
\shoveleft \text{Let }AD=CD=a, AB=AC=d, BD=3m \implies BC=\dfrac{d^2}{a}\\
\shoveleft \implies 3m=\dfrac{d^2}{a}-a=\dfrac{d^2-a^2}{a}\implies m=\dfrac{d^2-a^2}{3a}\\
\shoveleft \text{Let }G, H, M \text{ be the midpoints of }BE, AB, AF \text{ respectively }\\
\shoveleft \text{Let } \angle{ABC}=\angle{DAC}=\alpha \implies d=2acos\alpha, m=\dfrac{4cos^2\alpha-1}{3}a, 3m+a=4acos^2 \alpha\\
\shoveleft A(dcos\alpha, dsin\alpha),B(0,0) \implies H(\dfrac{dcos\alpha}{2}, \dfrac{dsin\alpha}{2})=(acos^2\alpha,asin\alpha cos \alpha)\\
\shoveleft G(m,0)=(\dfrac{4cos^2\alpha-1}{3}a, 0) \implies |GH|^2=\dfrac{cos^4\alpha-2cos^2\alpha+1}{9}a^2+2sin^2\alpha cos^2\alpha\\
\shoveleft |HC|^2=9a^2cos^4\alpha + a^2 sin^2\alpha cos^2\alpha \implies |GH|^2+|HC|^2=\dfrac{64cos^4\alpha+16cos^2\alpha+1}{9}a^2\\
\shoveleft |GC|^2=(4cos^2\alpha-\dfrac{4}{3}cos^2\alpha+\dfrac{1}{3})^2a^2=\dfrac{64cos^4\alpha+16cos^2\alpha+1}{9}a^2=|GH|^2+|HC|^2\\
\shoveleft \implies GH\ \perp CH, AF\parallel GH, AH=FH\implies AF \perp CH \implies M \text{ is on }CH\\
\shoveleft \implies \angle{AHC}=\angle{FHC}\implies \triangle{ACH}\cong\triangle{FCH}\implies AC=CF \blacksquare\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }AD=CD=a, AB=AC=d, BD=3m \implies BC=\dfrac{d^2}{a}\\
\shoveleft \implies 3m=\dfrac{d^2}{a}-a=\dfrac{d^2-a^2}{a}\implies m=\dfrac{d^2-a^2}{3a}\\
\shoveleft \text{Let }G, H, M \text{ be the midpoints of }BE, AB, AF \text{ respectively }\\
\shoveleft \text{Let } \angle{ABC}=\angle{DAC}=\alpha \implies d=2acos\alpha, m=\dfrac{4cos^2\alpha-1}{3}a, 3m+a=4acos^2 \alpha\\
\shoveleft A(dcos\alpha, dsin\alpha),B(0,0) \implies H(\dfrac{dcos\alpha}{2}, \dfrac{dsin\alpha}{2})=(acos^2\alpha,asin\alpha cos \alpha)\\
\shoveleft G(m,0)=(\dfrac{4cos^2\alpha-1}{3}a, 0) \implies |GH|^2=\dfrac{cos^4\alpha-2cos^2\alpha+1}{9}a^2+2sin^2\alpha cos^2\alpha\\
\shoveleft |HC|^2=9a^2cos^4\alpha + a^2 sin^2\alpha cos^2\alpha \implies |GH|^2+|HC|^2=\dfrac{64cos^4\alpha+16cos^2\alpha+1}{9}a^2\\
\shoveleft |GC|^2=(4cos^2\alpha-\dfrac{4}{3}cos^2\alpha+\dfrac{1}{3})^2a^2=\dfrac{64cos^4\alpha+16cos^2\alpha+1}{9}a^2=|GH|^2+|HC|^2\\
\shoveleft \implies GH\ \perp CH, AF\parallel GH, AH=FH\implies AF \perp CH \implies M \text{ is on }CH\\
\shoveleft \implies \angle{AHC}=\angle{FHC}\implies \triangle{ACH}\cong\triangle{FCH}\implies AC=CF \blacksquare\\
\end{multline}\)
Prove 2:
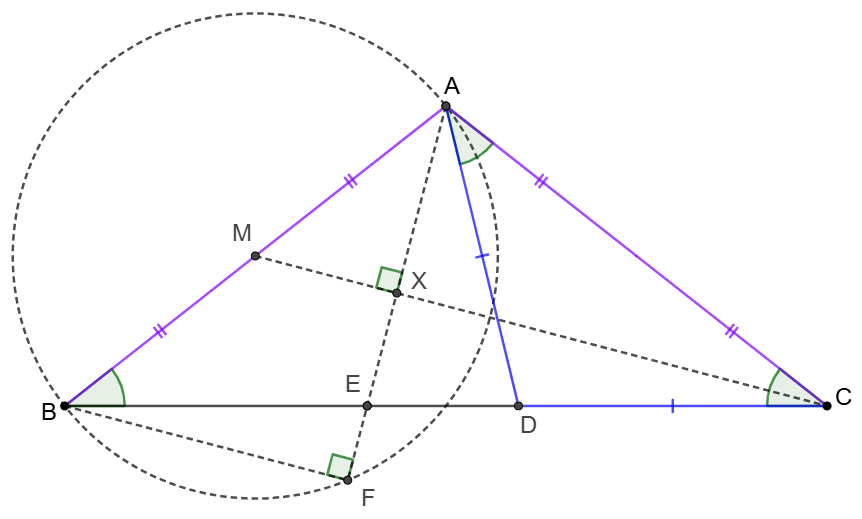 \(\begin{multline}
\shoveleft \text{Consider the structure in the physical way:} \\
\shoveleft \text{Let }M \text{ be the midpoint of }AB\\
\shoveleft E \text{ is a dynamic point on }BD \text{ to make } \angle{AFB}=90^{\circ}\\
\shoveleft \implies F \text{ is on the circle center at }M, \text{ diameter as }AB\\
\shoveleft AC=CF \implies C \text{ is on the perpendicular bisector of }AF\\
\shoveleft M \text{ is on perpendicular bisector of }AF \implies CM \text{ is the perpendicular bisector of }AF\\
\shoveleft C,M \text{are all fixed points in this structure } \implies \text{There is only one solution for }F\\
\shoveleft \implies \text{We can start from this position of }F \text{ to check }\dfrac{BE}{DE}\\
\shoveleft
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Consider the structure in the physical way:} \\
\shoveleft \text{Let }M \text{ be the midpoint of }AB\\
\shoveleft E \text{ is a dynamic point on }BD \text{ to make } \angle{AFB}=90^{\circ}\\
\shoveleft \implies F \text{ is on the circle center at }M, \text{ diameter as }AB\\
\shoveleft AC=CF \implies C \text{ is on the perpendicular bisector of }AF\\
\shoveleft M \text{ is on perpendicular bisector of }AF \implies CM \text{ is the perpendicular bisector of }AF\\
\shoveleft C,M \text{are all fixed points in this structure } \implies \text{There is only one solution for }F\\
\shoveleft \implies \text{We can start from this position of }F \text{ to check }\dfrac{BE}{DE}\\
\shoveleft
\end{multline}\)
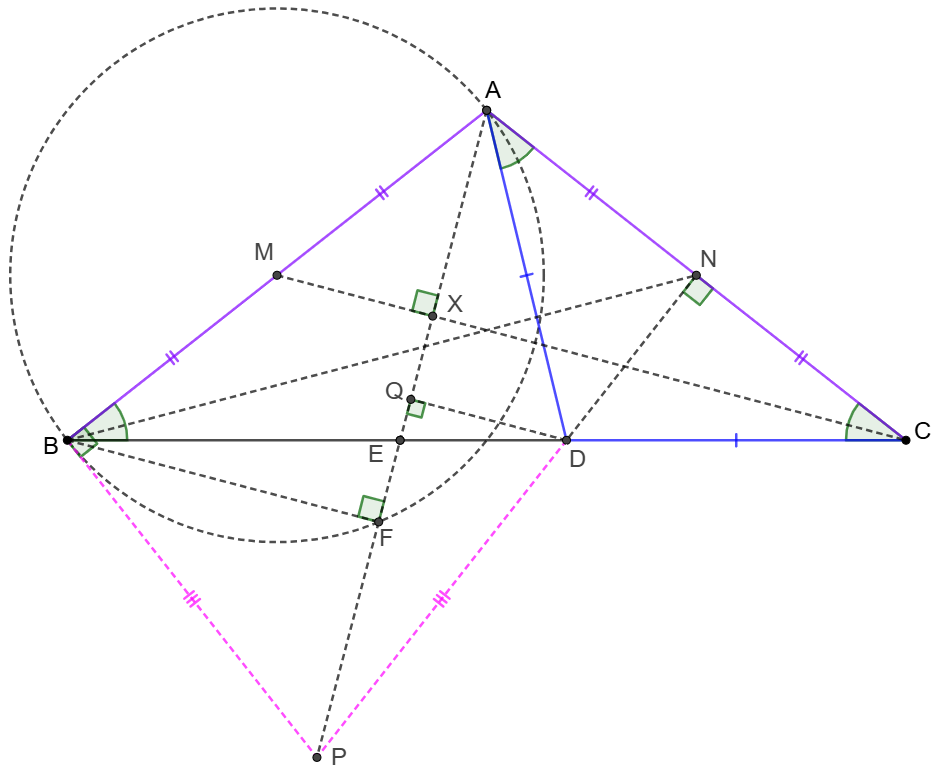 \(\begin{multline}
\shoveleft \text{Let }N \text{ be the midpoint of }AC, AF\cap DN=P, CM\cap AF=X\\
\shoveleft \implies AC\perp DN, AP\perp CM \implies \angle{ABN}=\angle{ACM}=90^{\circ}-\angle{XAN}=\angle{APN}\\
\shoveleft \implies ANPB \text{ is cyclic }\implies AB \perp BP \implies\\
\shoveleft \angle{PBD}=90^{\circ}-\angle{ABC}=90^{\circ}-\angle{ACB}=\angle{NDC}=\angle{BDP}\\
\shoveleft \implies BP=DP, AB=AC=2AN \implies [ABP]=2[ADP]\\
\shoveleft \text{Let }DQ\perp AP \text{ at }Q \implies BF=2DQ \implies BE=2DE \text{ then it's proved} \blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }N \text{ be the midpoint of }AC, AF\cap DN=P, CM\cap AF=X\\
\shoveleft \implies AC\perp DN, AP\perp CM \implies \angle{ABN}=\angle{ACM}=90^{\circ}-\angle{XAN}=\angle{APN}\\
\shoveleft \implies ANPB \text{ is cyclic }\implies AB \perp BP \implies\\
\shoveleft \angle{PBD}=90^{\circ}-\angle{ABC}=90^{\circ}-\angle{ACB}=\angle{NDC}=\angle{BDP}\\
\shoveleft \implies BP=DP, AB=AC=2AN \implies [ABP]=2[ADP]\\
\shoveleft \text{Let }DQ\perp AP \text{ at }Q \implies BF=2DQ \implies BE=2DE \text{ then it's proved} \blacksquare
\end{multline}\)
Prove 3:
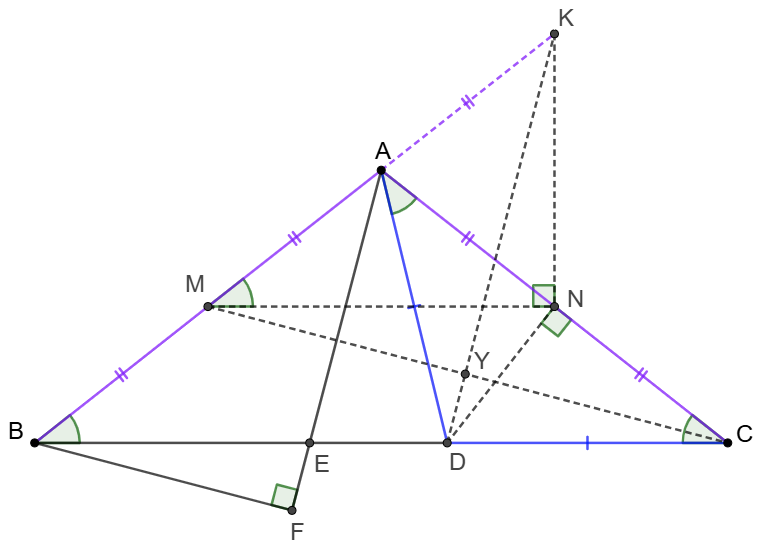 \(\begin{multline}
\shoveleft \text{Let }M, N \text{ be the midpoints of }AB, AC \text{ respectively} \\
\shoveleft \implies AM=AN, \angle{AMN}=\angle{ABC}=\angle{ACB}, DN\perp AC\\
\shoveleft \text{Extend }MA \text{ to }K \text{ such that }MA=AK , \text{ and let } MC\cap DK=Y \\
\shoveleft \implies KN\perp MN \implies \angle{KND}=90^{\circ}+\angle{MND}=\angle{MNC}\\
\shoveleft \angle{KMN}=\angle{DCN}\implies \dfrac{KN}{MN}=\dfrac{DN}{CN}\implies\\
\shoveleft \triangle{KND}\sim\triangle{MNC}\implies \angle{YMN}=\angle{YKN}\\
\shoveleft \implies KNYM \text{ is cyclic}\implies \angle{KYM}=\angle{KNM}=90^{\circ}\\
\shoveleft \dfrac{BA}{AK}=\dfrac{2}{1}=\dfrac{BE}{ED}\implies AF\parallel DK \implies AF \perp MC\\
\shoveleft AM=FM \implies \angle{AMC}=\angle{FMC}\implies \triangle{AMC}\cong\triangle{FMC}\\
\shoveleft \implies AC=FC\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }M, N \text{ be the midpoints of }AB, AC \text{ respectively} \\
\shoveleft \implies AM=AN, \angle{AMN}=\angle{ABC}=\angle{ACB}, DN\perp AC\\
\shoveleft \text{Extend }MA \text{ to }K \text{ such that }MA=AK , \text{ and let } MC\cap DK=Y \\
\shoveleft \implies KN\perp MN \implies \angle{KND}=90^{\circ}+\angle{MND}=\angle{MNC}\\
\shoveleft \angle{KMN}=\angle{DCN}\implies \dfrac{KN}{MN}=\dfrac{DN}{CN}\implies\\
\shoveleft \triangle{KND}\sim\triangle{MNC}\implies \angle{YMN}=\angle{YKN}\\
\shoveleft \implies KNYM \text{ is cyclic}\implies \angle{KYM}=\angle{KNM}=90^{\circ}\\
\shoveleft \dfrac{BA}{AK}=\dfrac{2}{1}=\dfrac{BE}{ED}\implies AF\parallel DK \implies AF \perp MC\\
\shoveleft AM=FM \implies \angle{AMC}=\angle{FMC}\implies \triangle{AMC}\cong\triangle{FMC}\\
\shoveleft \implies AC=FC\blacksquare
\end{multline}\)
07/19/2025
$E,F,G$ are on side $AB,BC,DA$ of square $ABCD$ respectively and $DE\perp FG, DE\cap FG=H$, $[AEHG]=1, [DGH]=4, [EBFH]=9$, find $[CDHF]$
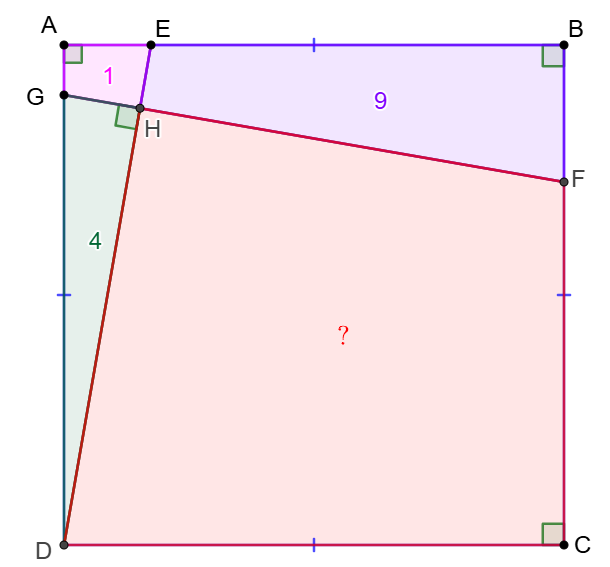
Solve:
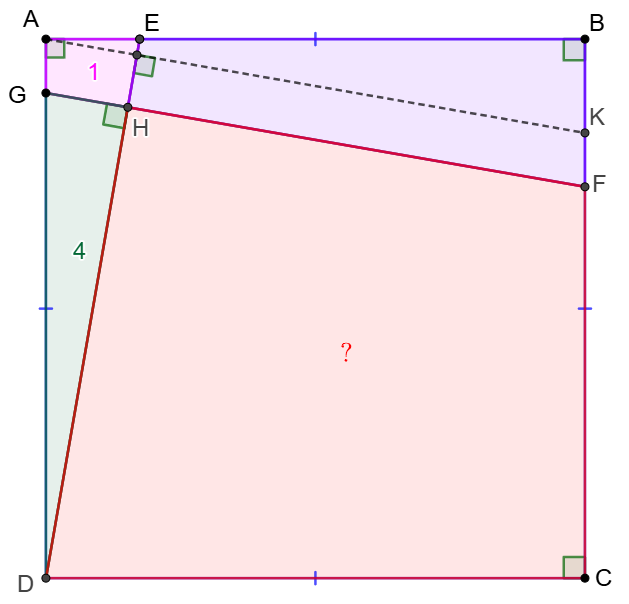 \(\begin{multline}
\shoveleft \text{Make }AK\perp DE, AK\cap BC=K, \text{Let }AD=AB=a, KF=b\\
\shoveleft \implies \triangle{ADE}\cong\triangle{BAK} \implies [ADE]=[BAK]=5 \\
\shoveleft \implies [AKFG]=1+9-5=5=[BAK], AG=KF=b\\
\shoveleft \implies [BAK]=\dfrac{AB\cdot BK}{2}=AB \cdot KF=ab\\
\shoveleft \implies BK=AE=2KF \implies AB\cdot KF=5 \implies ab=5\\
\shoveleft \triangle{DGH}\sim\triangle{DEA}\implies \dfrac{DH}{DA}=\dfrac{GH}{AE}=\sqrt{\dfrac{[DGH]}{[DEA]}}=\dfrac{2}{\sqrt{5}}\\
\shoveleft \implies GH=\dfrac{4}{\sqrt{5}}b, DH=\dfrac{2}{\sqrt{5}}a \implies AG=AD-\sqrt{GH^2+DH^2}\\
\shoveleft \implies b=a-\sqrt{\dfrac{16}{5}b^2+\dfrac{4}{5}a^2}\implies a=11b\implies b^2=\dfrac{5}{11}\\
\shoveleft \implies [ABCD]=a^2=121b^2=55\implies [CDHF]=55-1-4-9=\bbox[5px, border: 1px solid black]{41}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }AK\perp DE, AK\cap BC=K, \text{Let }AD=AB=a, KF=b\\
\shoveleft \implies \triangle{ADE}\cong\triangle{BAK} \implies [ADE]=[BAK]=5 \\
\shoveleft \implies [AKFG]=1+9-5=5=[BAK], AG=KF=b\\
\shoveleft \implies [BAK]=\dfrac{AB\cdot BK}{2}=AB \cdot KF=ab\\
\shoveleft \implies BK=AE=2KF \implies AB\cdot KF=5 \implies ab=5\\
\shoveleft \triangle{DGH}\sim\triangle{DEA}\implies \dfrac{DH}{DA}=\dfrac{GH}{AE}=\sqrt{\dfrac{[DGH]}{[DEA]}}=\dfrac{2}{\sqrt{5}}\\
\shoveleft \implies GH=\dfrac{4}{\sqrt{5}}b, DH=\dfrac{2}{\sqrt{5}}a \implies AG=AD-\sqrt{GH^2+DH^2}\\
\shoveleft \implies b=a-\sqrt{\dfrac{16}{5}b^2+\dfrac{4}{5}a^2}\implies a=11b\implies b^2=\dfrac{5}{11}\\
\shoveleft \implies [ABCD]=a^2=121b^2=55\implies [CDHF]=55-1-4-9=\bbox[5px, border: 1px solid black]{41}
\end{multline}\)
Solve 2: \(\begin{multline} \shoveleft \text{Make }AK\perp DE, AK\cap BC=K, \text{Let }AD=AB=a, KF=b\\ \shoveleft \implies \triangle{ADE}\cong\triangle{BAK} \implies [ADE]=[BAK]=5 \\ \shoveleft \implies [AKFG]=1+9-5=5=[BAK], AG=KF=b\\ \shoveleft \implies [BAK]=\dfrac{AB\cdot BK}{2}=AB \cdot KF=ab\\ \shoveleft \implies BK=AE=2KF=2AG=2b \implies AB\cdot KF=5 \implies ab=5\\ \shoveleft \triangle{DGH}\sim\triangle{DEA}\implies \dfrac{DH}{DA}=\dfrac{GH}{AE}=\sqrt{\dfrac{[DGH]}{[DEA]}}=\dfrac{2}{\sqrt{5}}\\ \shoveleft \implies GH=\dfrac{4}{\sqrt{5}}b, GE^2=5b^2 \implies EH=\dfrac{3}{\sqrt{5}}b \implies [AEHG]=b^2+\dfrac{6}{5}b^2=1\\ \shoveleft \implies b=\sqrt{\dfrac{5}{11}} \implies a=\sqrt{55} \implies [ABCD]=a^2=121b^2=55\\ \shoveleft \implies [CDHF]=55-1-4-9=\bbox[5px, border: 1px solid black]{41} \end{multline}\)
07/29/2025
$ABCD$ is a quadrilateral such that $\angle{CAD}=10^{\circ}$, $\angle{BAC}=20^{\circ}$, $\angle{ACB}=30^{\circ}$, $\angle{ACD}=40^{\circ}$, $AC\cap BD=E$, find $\angle{AED}$.
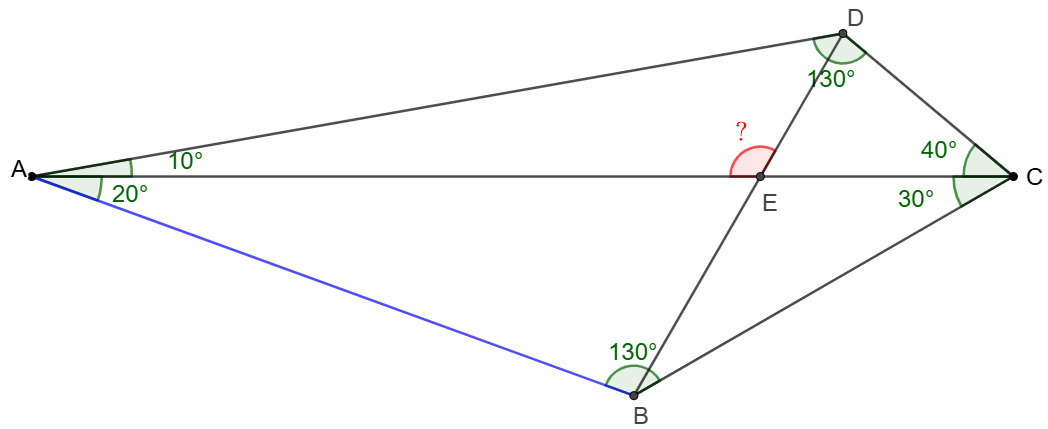
Solve:
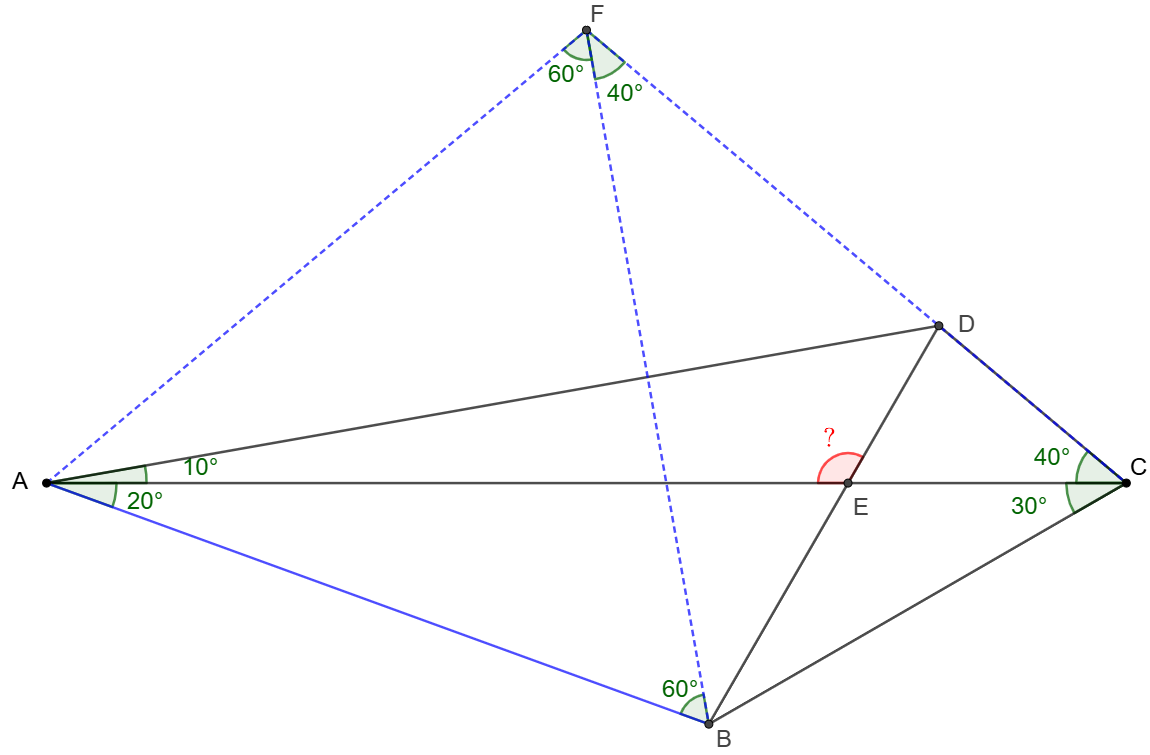 \(\begin{multline}
\shoveleft \text{Let }F \text{ be the circumcenter of }\triangle{ABC} \implies AF=BF=CF\\
\shoveleft \angle{AFB}=2\angle{ACB}=60^{\circ}, \angle{BFC}=2\angle{BAC}=40^{\circ}\\
\shoveleft \implies ABF\text{ is equilateral}, \angle{FCB}=\angle{FBC}=70^{\circ}\\
\shoveleft \implies CDF\text{ is collinear}, AB=AF, \angle{FAD}=\angle{BAD}\\
\shoveleft \implies \triangle{FAD}\cong\triangle{BAD}\implies FD=BD \\
\shoveleft \implies \angle{BDC}=2\angle{BFC}=80^{\circ}\implies \angle{AED}=\bbox[5px, border: 1px solid black]{120^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }F \text{ be the circumcenter of }\triangle{ABC} \implies AF=BF=CF\\
\shoveleft \angle{AFB}=2\angle{ACB}=60^{\circ}, \angle{BFC}=2\angle{BAC}=40^{\circ}\\
\shoveleft \implies ABF\text{ is equilateral}, \angle{FCB}=\angle{FBC}=70^{\circ}\\
\shoveleft \implies CDF\text{ is collinear}, AB=AF, \angle{FAD}=\angle{BAD}\\
\shoveleft \implies \triangle{FAD}\cong\triangle{BAD}\implies FD=BD \\
\shoveleft \implies \angle{BDC}=2\angle{BFC}=80^{\circ}\implies \angle{AED}=\bbox[5px, border: 1px solid black]{120^{\circ}}
\end{multline}\)