06/12/2025
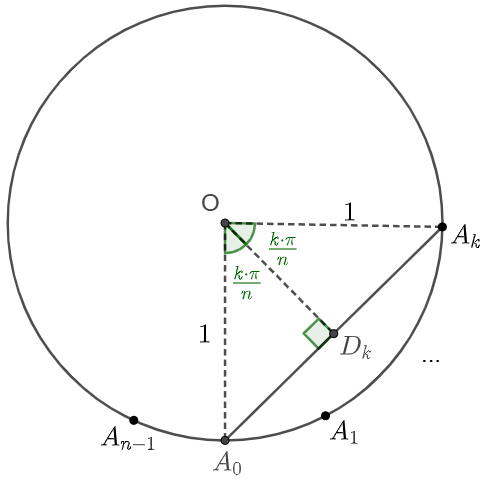
Consider a regular n-gon inscribed in the unit circle. Pick one vertex. Now connect it with line segments to all the other vertices. What is the value of the product of all the lengths of the segments?
Solve:
 \(\begin{multline}
\shoveleft \text{Suppose }A_0, A_1, ... A_{n-1} \text{ are the vertices of this regular n-gon inscribed in the unit circle}\\
\shoveleft \text{Make }OD_k\perp A_0A_k \implies \angle{A_0OA_k}=\dfrac{k \cdot 2\pi}{n} \implies \angle{A_0OD_k=\dfrac{k\pi}{n}}, k=1, 2, ..., (n-1)\\
\shoveleft \implies A_0A_k=2 \cdot sin(\dfrac{k\pi}{n}) \implies ans=\displaystyle\prod_{i=1}^{n-1}{|A_0A_i|}=2^{n-1}\prod_{k=1}^{n-1}sin(\dfrac{k\pi}{n})\\
\shoveleft sin(\dfrac{k\pi}{n})=\dfrac{e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}}}{2i}\implies ans=2^{n-1}\prod_{k=1}^{n-1}{\dfrac{e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}}}{2i}}=\dfrac{2^{n-1}}{(2i)^{n-1}}\prod_{k=1}^{n-1}{(e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}})}\\
\shoveleft =\dfrac{1}{i^{n-1}}e^{-i(\tfrac{\pi+2\pi+...+(n-1)\pi}{n})}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}=\dfrac{1}{i^{n-1}}e^{-i\tfrac{n(n-1)\pi}{2n}}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}\\
\shoveleft i=e^{i\tfrac{\pi}{2}} \implies \dfrac{1}{i^{n-1}}e^{-i\tfrac{(n-1)\pi}{2}}=i^{-2(n-1)}=(-1)^{n-1}\implies ans=(-1)^{n-1}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}=\prod_{k=1}^{n-1}{(1-e^{2i\tfrac{k\pi}{n}})}\\
\shoveleft 1, e^{2i\tfrac{k\pi}{n}}, k=1, 2, ..., n-1 \text{ are the roots of equation } z^n-1=0 \implies (z-1)\prod_{k=1}^{n-1}{(z-e^{2i\tfrac{k\pi}{n}})}=0=z^n-1\\
\shoveleft \implies \dfrac{z^n-1}{z-1}=\prod_{k=1}^{n-1}{(z-e^{2i\tfrac{k\pi}{n}})}=z^{n-1}+z^{n-2}+...+1 \implies \prod_{k=1}^{n-1}{(1-e^{2i\tfrac{k\pi}{n}})}=\sum_{k=0}^{n-1}{1^{k}}=n\implies ans=\bbox[5px, border: 1px solid black]{n}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Suppose }A_0, A_1, ... A_{n-1} \text{ are the vertices of this regular n-gon inscribed in the unit circle}\\
\shoveleft \text{Make }OD_k\perp A_0A_k \implies \angle{A_0OA_k}=\dfrac{k \cdot 2\pi}{n} \implies \angle{A_0OD_k=\dfrac{k\pi}{n}}, k=1, 2, ..., (n-1)\\
\shoveleft \implies A_0A_k=2 \cdot sin(\dfrac{k\pi}{n}) \implies ans=\displaystyle\prod_{i=1}^{n-1}{|A_0A_i|}=2^{n-1}\prod_{k=1}^{n-1}sin(\dfrac{k\pi}{n})\\
\shoveleft sin(\dfrac{k\pi}{n})=\dfrac{e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}}}{2i}\implies ans=2^{n-1}\prod_{k=1}^{n-1}{\dfrac{e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}}}{2i}}=\dfrac{2^{n-1}}{(2i)^{n-1}}\prod_{k=1}^{n-1}{(e^{i\tfrac{k\pi}{n}}-e^{-i\tfrac{k\pi}{n}})}\\
\shoveleft =\dfrac{1}{i^{n-1}}e^{-i(\tfrac{\pi+2\pi+...+(n-1)\pi}{n})}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}=\dfrac{1}{i^{n-1}}e^{-i\tfrac{n(n-1)\pi}{2n}}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}\\
\shoveleft i=e^{i\tfrac{\pi}{2}} \implies \dfrac{1}{i^{n-1}}e^{-i\tfrac{(n-1)\pi}{2}}=i^{-2(n-1)}=(-1)^{n-1}\implies ans=(-1)^{n-1}\prod_{k=1}^{n-1}{(e^{2i\tfrac{k\pi}{n}}-1)}=\prod_{k=1}^{n-1}{(1-e^{2i\tfrac{k\pi}{n}})}\\
\shoveleft 1, e^{2i\tfrac{k\pi}{n}}, k=1, 2, ..., n-1 \text{ are the roots of equation } z^n-1=0 \implies (z-1)\prod_{k=1}^{n-1}{(z-e^{2i\tfrac{k\pi}{n}})}=0=z^n-1\\
\shoveleft \implies \dfrac{z^n-1}{z-1}=\prod_{k=1}^{n-1}{(z-e^{2i\tfrac{k\pi}{n}})}=z^{n-1}+z^{n-2}+...+1 \implies \prod_{k=1}^{n-1}{(1-e^{2i\tfrac{k\pi}{n}})}=\sum_{k=0}^{n-1}{1^{k}}=n\implies ans=\bbox[5px, border: 1px solid black]{n}
\end{multline}\)
06/15/2025
The function $f$ is defined by $f(x)=\dfrac{ax+b}{cx+d}$, where $a,b,c$ and $d$ are nonzero real numbers, has the properties $f(19)=19, f(97)=97$, and $f(f(x))=x$ for all values of $x$ except $-d/c$. Find the unique number that is not in the range of $f$.
Solve: \(\begin{multline} \shoveleft f(f(x))=\dfrac{a\dfrac{\dfrac{ax+b}{cx+d}}{}+b}{c\dfrac{ax+b}{cx+d}+d}=\dfrac{a^2x+ab+bcx+bd}{acx+bc+cdx+d^2}=\dfrac{(a^2+bc)x+b(a+d)}{c(a+d)x+(bc+d^2)}=x\\ \shoveleft \implies x\ne-\dfrac{bc+d^2}{c(a+d)}, -c(a+d)x^2+(a^2-d^2)x+b(a+d)=0\\ \shoveleft \implies c(a+d)=0, a^2=d^2, b(a+d)=0\\ \shoveleft f(19)=\dfrac{19a+b}{19c+d}=19 \implies 19a+b=19^2c+19d\\ \shoveleft f(97)=\dfrac{97a+b}{97c+d}=97 \implies 97a+b=97^2c+97d\\ \shoveleft \implies a-d=116c \ne 0 \implies a+d=0\\ \shoveleft \implies f(x)=\dfrac{ax+b}{cx-a}, a-d=2a=116c \implies \dfrac{a}{c}=58\implies a=58c\\ \shoveleft f(x)=\dfrac{ax+b}{cx-a}=\dfrac{58cx+b}{cx-58c}=58+\dfrac{b+58^2c}{c(x-58)}\\ \shoveleft \text{if }\dfrac{b+58^2c}{c(x-58)}=0 \implies f(x)=58 \implies f(19)=f(97)=58\\ \shoveleft \text{So }f(x)\ne \bbox[5px, border: 1px solid black]{58} \end{multline}\)
06/24/2025
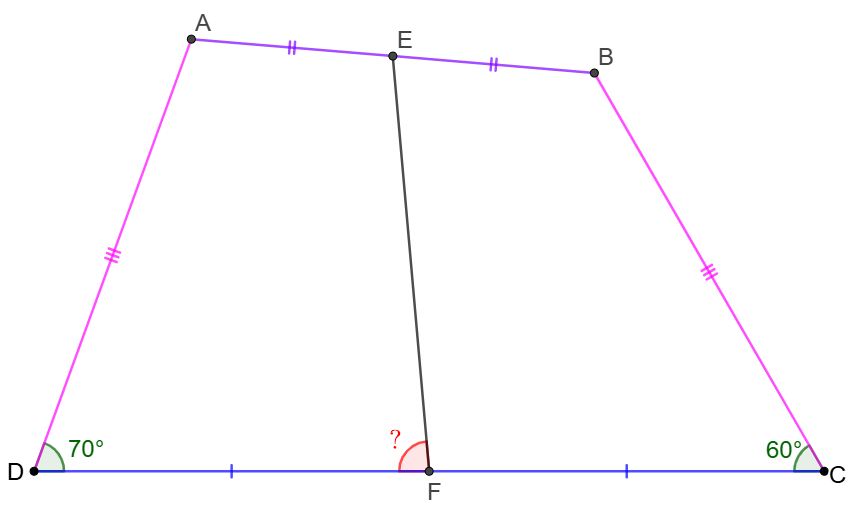
$ABCD$ is a quadrilateral such that $AD=BC, \angle{ADC}=70^{\circ}, \angle{BCD}=60^{\circ}$, $E,F$ are the midpoint of $AB, CD$ respectively. Find $\angle{DFE}$.
Solve:
 \(\begin{multline}
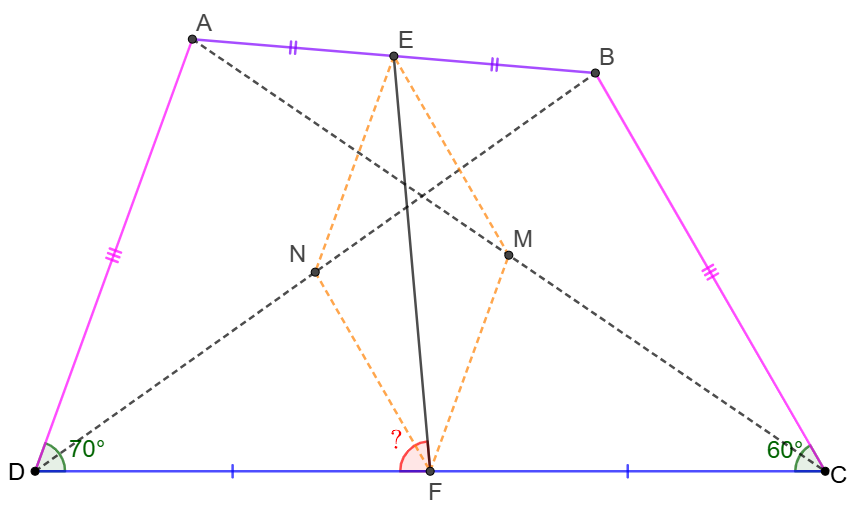
\shoveleft \text{Let }M,N \text{ be the midpoint of }AC, BD \text{ respectively } \\
\shoveleft \implies EM\parallel BC \parallel NF, FM \parallel AD \parallel EN\\
\shoveleft FM=\dfrac{AD}{2}=EN=\dfrac{BC}{2}=EM=NF\\
\shoveleft \implies \angle{DFN}=60^{\circ}, \angle{CFM}=70^{\circ}, EMFN \text{ is a rhombus}\\
\shoveleft \implies\angle{EFN}=\angle{EFM}=\dfrac{180^{\circ}-60^{\circ}-70^{\circ}}{2}=25^{\circ}\\
\shoveleft \implies \angle{DFE}=\angle{DFN}+\angle{EFN}=60^{\circ}+25^{\circ}=\bbox[5px, border: 1px solid black]{85^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }M,N \text{ be the midpoint of }AC, BD \text{ respectively } \\
\shoveleft \implies EM\parallel BC \parallel NF, FM \parallel AD \parallel EN\\
\shoveleft FM=\dfrac{AD}{2}=EN=\dfrac{BC}{2}=EM=NF\\
\shoveleft \implies \angle{DFN}=60^{\circ}, \angle{CFM}=70^{\circ}, EMFN \text{ is a rhombus}\\
\shoveleft \implies\angle{EFN}=\angle{EFM}=\dfrac{180^{\circ}-60^{\circ}-70^{\circ}}{2}=25^{\circ}\\
\shoveleft \implies \angle{DFE}=\angle{DFN}+\angle{EFN}=60^{\circ}+25^{\circ}=\bbox[5px, border: 1px solid black]{85^{\circ}}
\end{multline}\)
06/25/2025
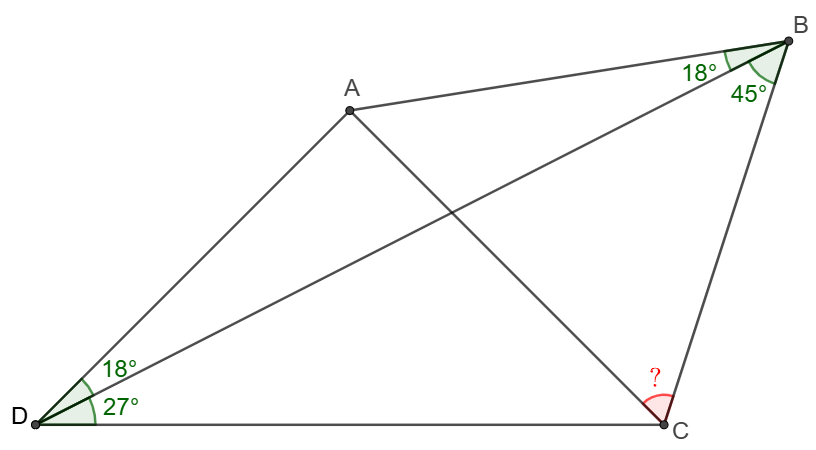
$ABCD$ is a quadrilateral such that $\angle{ABD}=\angle{ADB}=18^{\circ}$, $\angle{CDB}=27^{\circ}$,$\angle{CBD}=45^{\circ}$ find $\angle{ACB}$.
Solve 1:
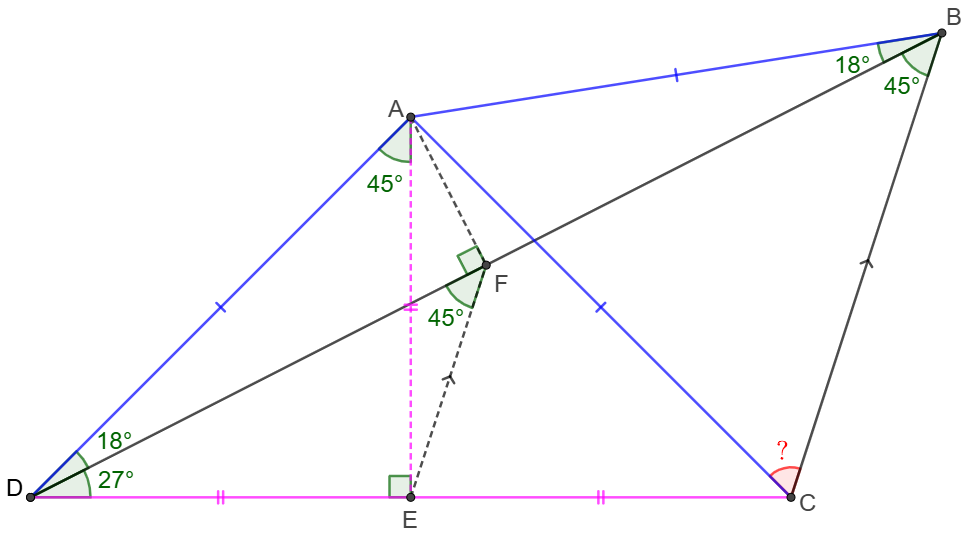 \(\begin{multline}
\shoveleft \text{Make }E, F \text{ on }CD, BD \text{ respectively such that }AE\perp CD, AF\perp BD \\
\shoveleft \implies AFED \text{ is cyclic},\angle{ADE}=45^{\circ}\\
\shoveleft \implies \angle{DAE}=\angle{DFE}=45^{\circ}=\angle{CBD}\implies EF \parallel BC\\
\shoveleft \angle{ADB}=\angle{ABD}\implies DF=BF\implies DE=EC\\
\shoveleft \implies AD=AC=AB\implies \angle{ACB}=\angle{ABC}=\bbox[5px, border: 1px solid black]{63^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }E, F \text{ on }CD, BD \text{ respectively such that }AE\perp CD, AF\perp BD \\
\shoveleft \implies AFED \text{ is cyclic},\angle{ADE}=45^{\circ}\\
\shoveleft \implies \angle{DAE}=\angle{DFE}=45^{\circ}=\angle{CBD}\implies EF \parallel BC\\
\shoveleft \angle{ADB}=\angle{ABD}\implies DF=BF\implies DE=EC\\
\shoveleft \implies AD=AC=AB\implies \angle{ACB}=\angle{ABC}=\bbox[5px, border: 1px solid black]{63^{\circ}}
\end{multline}\)
Solve 2:
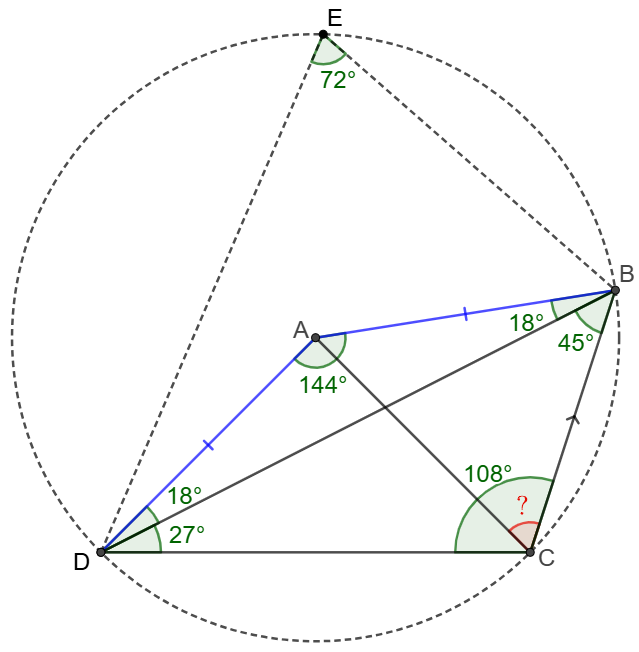 \(\begin{multline}
\shoveleft \text{Let }E \text{ be a point on circumcircle of }\triangle{BCD}\\
\shoveleft \angle{BCD}=108^{\circ}\implies \angle{BED}=72^{\circ}\\
\shoveleft \angle{BAD}=144^{\circ}=2\angle{BED}, AB=AD\\
\shoveleft \implies A \text{ is circumcenter of }\triangle{BDE}\\
\shoveleft \implies A \text{ is circumcenter of }\triangle{BCD}\\
\shoveleft \implies AB=AC \implies \angle{ACB}=\angle{ABC}=\bbox[5px, border: 1px solid black]{63^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be a point on circumcircle of }\triangle{BCD}\\
\shoveleft \angle{BCD}=108^{\circ}\implies \angle{BED}=72^{\circ}\\
\shoveleft \angle{BAD}=144^{\circ}=2\angle{BED}, AB=AD\\
\shoveleft \implies A \text{ is circumcenter of }\triangle{BDE}\\
\shoveleft \implies A \text{ is circumcenter of }\triangle{BCD}\\
\shoveleft \implies AB=AC \implies \angle{ACB}=\angle{ABC}=\bbox[5px, border: 1px solid black]{63^{\circ}}
\end{multline}\)
06/28/2025
2025 Youth Balkan Mathematics Olympic Problem 3: $\angle{BAC}=90^{\circ}$ in $\triangle{ABC}$ and $AD$ is the attitude of side $BC$. $E$ is the midpoint of $CD$. The circumcircle of $\triangle{ABD}$ meets $AE$ at $F$. Extended $BA$ and $DF$ meet at $X$. Show that $CX=DX$.
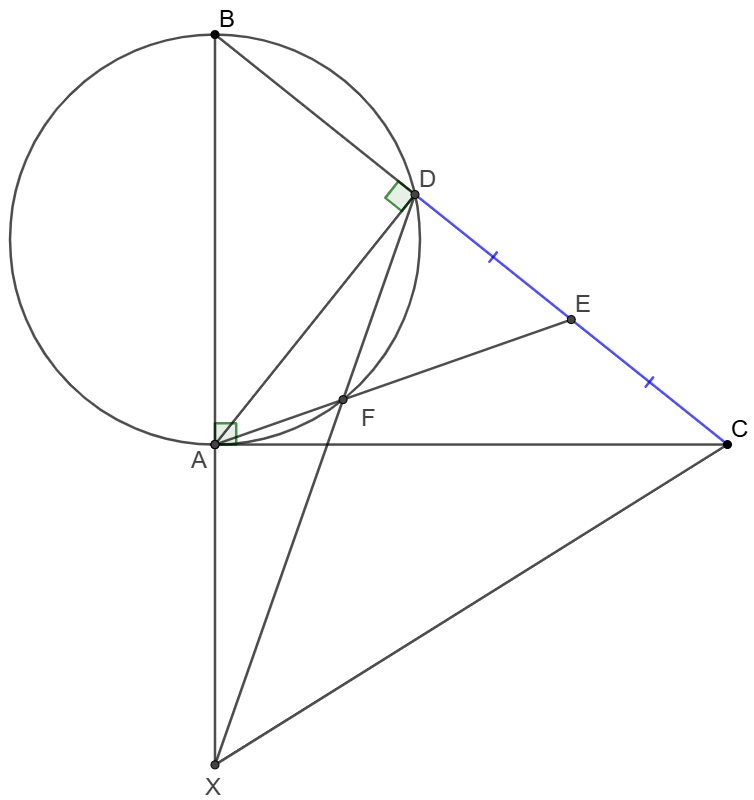
Prove 1:
 \(\begin{multline}
\shoveleft \text{Let } M \text{ be the midpoint of }AC, AD \cap BF=H, F \text{ is on }\odot{ABD} \\
\shoveleft \implies \angle{AFB}=\angle{ADB}=90^{\circ} \implies H \text{ is the orthocenter of }\triangle{ABE}\\
\shoveleft \implies EH \perp AB \implies EH \parallel AC, DE=CE \implies DH=AH\\
\shoveleft ABDF \text{ cyclic }\implies \triangle{ABH}\sim\triangle{FDH}, \triangle{BDH}\sim\triangle{AFH}, \triangle{XAF }\sim\triangle{XDB}\\
\shoveleft \implies \dfrac{XA}{DX}=\dfrac{AF}{BD}=\dfrac{FH}{DH}=\dfrac{FH}{AH}=\dfrac{DF}{AB}=\dfrac{FX}{BX}\implies \dfrac{DF}{FX}=\dfrac{AB}{BX}\\
\shoveleft \text{Apply Menelaus's Theorem on line }AFE \text{ and }\triangle{BDX} \implies \dfrac{DF}{FX}\dfrac{XA}{AB}\dfrac{BE}{DE}=1\\
\shoveleft \implies \dfrac{AB}{BX}\dfrac{XA}{AB}\dfrac{BE}{DE}=1\implies \dfrac{XA}{BX}=\dfrac{DE}{BE}=\dfrac{CE}{BE}\implies \dfrac{BE}{CE}\dfrac{CM}{MA}\dfrac{XA}{BX}=1\\
\shoveleft \implies AME \text{ are collinear by } \text{Menelaus's Theorem on }\triangle{ABC}\\
\shoveleft ME \parallel AD, AD \perp BC \implies XE \perp BC,DE=CE \implies XC=XD \blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}
\shoveleft \text{Let } M \text{ be the midpoint of }AC, AD \cap BF=H, F \text{ is on }\odot{ABD} \\
\shoveleft \implies \angle{AFB}=\angle{ADB}=90^{\circ} \implies H \text{ is the orthocenter of }\triangle{ABE}\\
\shoveleft \implies EH \perp AB \implies EH \parallel AC, DE=CE \implies DH=AH\\
\shoveleft ABDF \text{ cyclic }\implies \triangle{ABH}\sim\triangle{FDH}, \triangle{BDH}\sim\triangle{AFH}, \triangle{XAF }\sim\triangle{XDB}\\
\shoveleft \implies \dfrac{XA}{DX}=\dfrac{AF}{BD}=\dfrac{FH}{DH}=\dfrac{FH}{AH}=\dfrac{DF}{AB}=\dfrac{FX}{BX}\implies \dfrac{DF}{FX}=\dfrac{AB}{BX}\\
\shoveleft \text{Apply Menelaus's Theorem on line }AFE \text{ and }\triangle{BDX} \implies \dfrac{DF}{FX}\dfrac{XA}{AB}\dfrac{BE}{DE}=1\\
\shoveleft \implies \dfrac{AB}{BX}\dfrac{XA}{AB}\dfrac{BE}{DE}=1\implies \dfrac{XA}{BX}=\dfrac{DE}{BE}=\dfrac{CE}{BE}\implies \dfrac{BE}{CE}\dfrac{CM}{MA}\dfrac{XA}{BX}=1\\
\shoveleft \implies AME \text{ are collinear by } \text{Menelaus's Theorem on }\triangle{ABC}\\
\shoveleft ME \parallel AD, AD \perp BC \implies XE \perp BC,DE=CE \implies XC=XD \blacksquare
\end{multline}\)
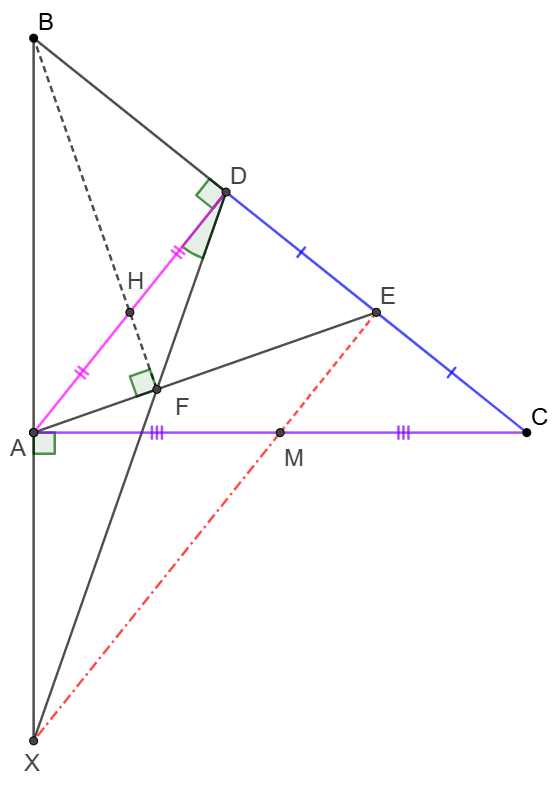
Prove 2:
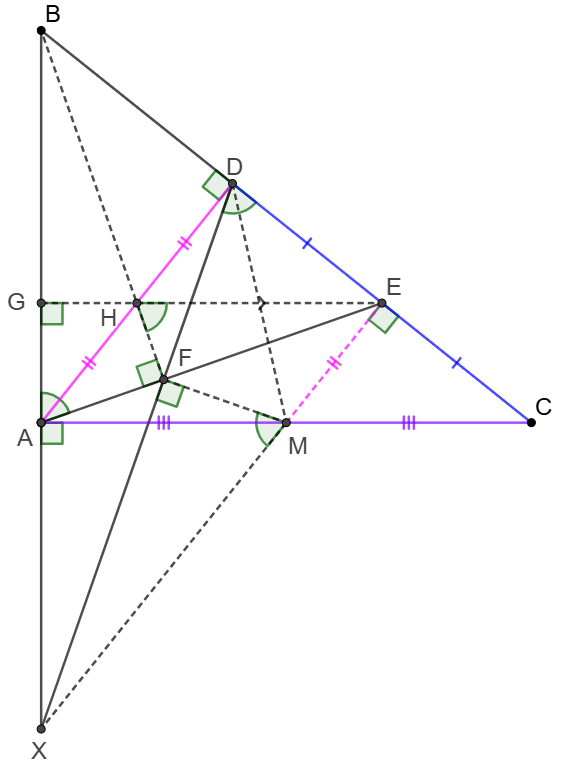 \(\begin{multline}
\shoveleft \text{Let } M \text{ be the midpoint of }AC, AD \cap BF=H, F \text{ is on }\odot{ABD} \\
\shoveleft \implies \angle{AFB}=\angle{ADB}=90^{\circ} \implies H \text{ is the orthocenter of }\triangle{ABE}\\
\shoveleft \implies AFHG, DEFH, BDHG \text{ are all cyclic}\\
\shoveleft \implies EH \perp AB \implies EH \parallel AC, DE=CE \implies DH=AH=EM\\
\shoveleft \implies DEMH \text{ is rectangle }\implies DEMFH \text{ is cyclic}\implies XF\perp FM\\
\shoveleft \implies AFMX \text{ is cyclic }\implies \angle{FMX}=\angle{FAG}=\angle{EHF}=\angle{EDF}\\
\shoveleft =\angle{FDM}+\angle{EDM}=\angle{FEM}+\angle{EFM}\implies EMX \text{ is collinear}\\
\shoveleft ME \parallel AD, AD \perp BC \implies XE \perp BC,DE=CE \implies XC=XD \blacksquare
\end{multline}\)
Prove 3:
\(\begin{multline}
\shoveleft \text{Let } M \text{ be the midpoint of }AC, AD \cap BF=H, F \text{ is on }\odot{ABD} \\
\shoveleft \implies \angle{AFB}=\angle{ADB}=90^{\circ} \implies H \text{ is the orthocenter of }\triangle{ABE}\\
\shoveleft \implies AFHG, DEFH, BDHG \text{ are all cyclic}\\
\shoveleft \implies EH \perp AB \implies EH \parallel AC, DE=CE \implies DH=AH=EM\\
\shoveleft \implies DEMH \text{ is rectangle }\implies DEMFH \text{ is cyclic}\implies XF\perp FM\\
\shoveleft \implies AFMX \text{ is cyclic }\implies \angle{FMX}=\angle{FAG}=\angle{EHF}=\angle{EDF}\\
\shoveleft =\angle{FDM}+\angle{EDM}=\angle{FEM}+\angle{EFM}\implies EMX \text{ is collinear}\\
\shoveleft ME \parallel AD, AD \perp BC \implies XE \perp BC,DE=CE \implies XC=XD \blacksquare
\end{multline}\)
Prove 3:
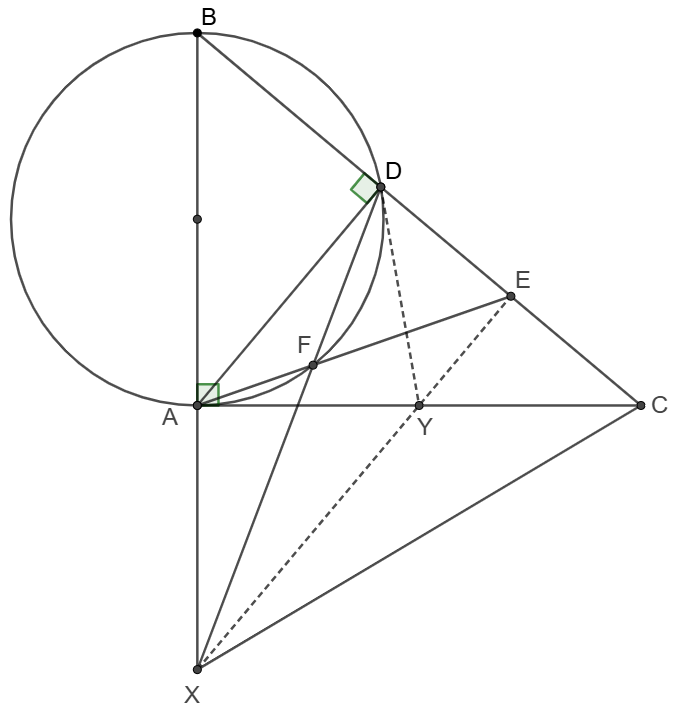 \(\begin{multline}
\shoveleft \text{Make }DY \text{ tangent to the circumcircle of }\triangle{ABD}, DY \cap AC=Y\\
\shoveleft \implies \angle{YAD}=\angle{ABD}=\angle{ADY}\implies AY=DY \implies AY=YC\\
\shoveleft \text{Apply }\href{https://en.wikipedia.org/wiki/Pascal%27s_theorem}{\text{Pascal's Theorem }} \text{ to hexagon }AABDDF: \\
\shoveleft BD\cap AF=E, BA\cap DF=X, AA\cap DD=Y \implies XYE \text{ is collinear}\\
\shoveleft EY\parallel AD \implies EY\perp CD \implies XE \text{ is perpendicular bisector of }CD\\
\shoveleft \implies XC=XD\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }DY \text{ tangent to the circumcircle of }\triangle{ABD}, DY \cap AC=Y\\
\shoveleft \implies \angle{YAD}=\angle{ABD}=\angle{ADY}\implies AY=DY \implies AY=YC\\
\shoveleft \text{Apply }\href{https://en.wikipedia.org/wiki/Pascal%27s_theorem}{\text{Pascal's Theorem }} \text{ to hexagon }AABDDF: \\
\shoveleft BD\cap AF=E, BA\cap DF=X, AA\cap DD=Y \implies XYE \text{ is collinear}\\
\shoveleft EY\parallel AD \implies EY\perp CD \implies XE \text{ is perpendicular bisector of }CD\\
\shoveleft \implies XC=XD\blacksquare
\end{multline}\)