M∀TH Workout

May 2025

 
  • May 01, 2025

05/01/2025

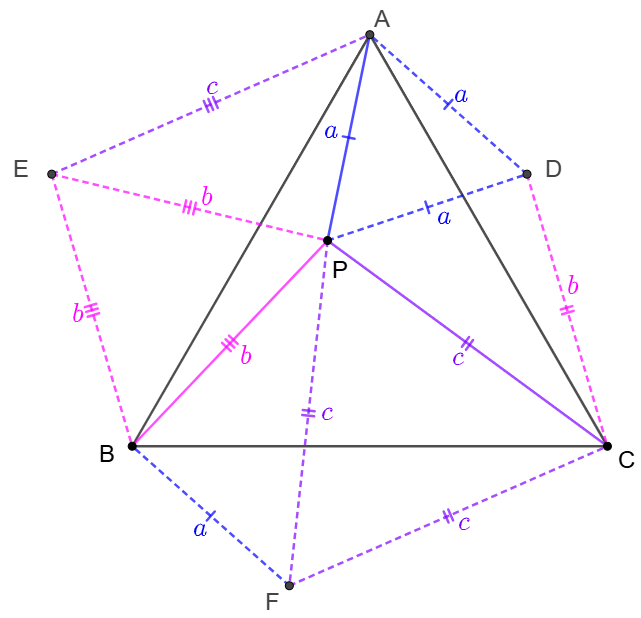
$P$ is a point inside the equilateral triangle $\triangle{ABC}$ and $PA=a,PB=b,PC=c$, find $[ABC]$.

Solve:

image-20250501205154078 \(\begin{multline} \shoveleft \text{Make equilateral triangles }\triangle{APD}, \triangle{BPE}, \triangle{CPF} \implies \\ \shoveleft \triangle{ACD}\cong\triangle{ABP}, \triangle{ABE}\cong\triangle{CBP},\triangle{CBF}\cong\triangle{CAP}\\ \shoveleft \triangle{AEP}\cong\triangle{BFP}\cong\triangle{CDP}\implies [APD]+[CDP]=[ABP]+[CAP]\\ \shoveleft [CFP]+[BFP]=[BCP]+[CAP],[BEP]+[AEP]=[ABP]+[BCP]\\ \shoveleft \implies 2[ABC]=[ADP]+[BEP]+[CFP]+3[CDP]\implies\\ \shoveleft [ABC]=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{3}}{8}(a^2+b^2+c^2)+\dfrac{3}{2}\sqrt{p(p-a)(p-b)(p-c)}, p=\dfrac{a+b+c}{2}} \end{multline}\)

05/02/2025

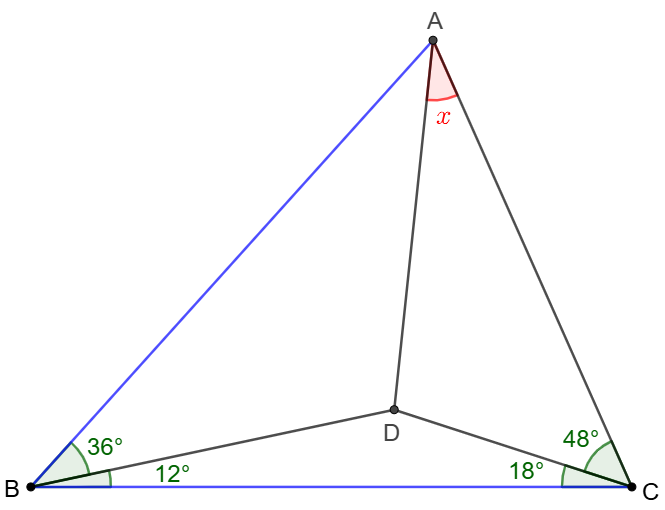
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=36^{\circ}$,$\angle{CBD}=12^{\circ}$, $\angle{ACD}=48^{\circ}$, $\angle{BCD}=18^{\circ}$. Find $\angle{CAD}$.

image-20250502224214563

Solve:

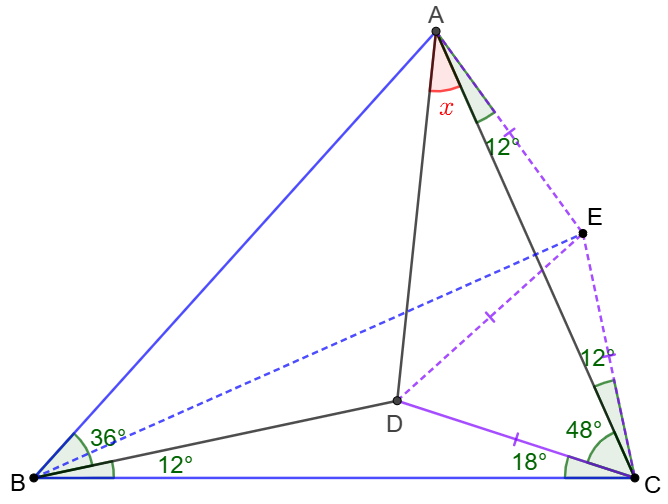
image-20250502224440096 \(\begin{multline} \shoveleft \angle{BAC}=66^{\circ}=\angle{BCA}\implies BA=BC\\ \shoveleft \text{Let }E \text{ be the mirror of }C \text{ along }BD \implies\\ \shoveleft \angle{DBE}=\angle{CBD}=12^{\circ}, \angle{BED}=\angle{BCD}=18^{\circ}\\ \shoveleft BE=BC=BA, DE=CD \implies \\ \shoveleft \angle{ABE}=\angle{EBC}=24^{\circ},\angle{CDE}=60^{\circ}\\ \shoveleft \implies \angle{AEB}=\angle{ECB}=78^{\circ},\triangle{CDE}\text{ is equilateral}\\ \shoveleft \implies AE=CE=DE=CD \\ \shoveleft \implies \angle{AED}=96^{\circ}\implies \angle{ADE}=\angle{DAE}=42^{\circ}\\ \shoveleft \implies \angle{CAD}=42^{\circ}-12^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

05/11/2025

solve system $\sqrt{x}+y=11, x+\sqrt{y}=7$

Solve: \(\begin{multline} \shoveleft \text{By observation we can see } x=4, y=9 \text{ is one solution}\\ \shoveleft \text{Let }a=\sqrt{x}, b=\sqrt{y}\implies a+b^2=11, a^2+b=7\\ \shoveleft \implies a=11-b^2 \implies (11-b^2)^2+b=7\\ \shoveleft \implies b^4-22b^2+b+114=0 \implies (b-3)(b^3+3b^2-13b-38)=0\\ \shoveleft \text{Now solve }f(b)=b^3+3b^2-13b-38=0, 0<b<7 \\ \shoveleft \text{Two inflection points when }f'(b)=0 \implies 3b^2+6b-13=0 \implies \\ \shoveleft b=\dfrac{-6\pm\sqrt{36+156}}{6}=-1\pm\dfrac{4\sqrt{3}}{3}, \text{ and }f(-1+\dfrac{4\sqrt{3}}{3})<0, f(7)>0\\ \shoveleft -1+\dfrac{4\sqrt{3}}{3}<b=\sqrt{y}=3<7 \implies \text{ it is the only root for }f(b)=0, 0<b<7\\ \shoveleft \implies \text{The only root for original system is: }\bbox[5px, border: 1px solid black]{x=4,y=9} \end{multline}\)

05/14/2025

$E$ is a point inside square $ABCD$ such that $AE=3, BE=2, CE=1$, find $\angle{BEC}$

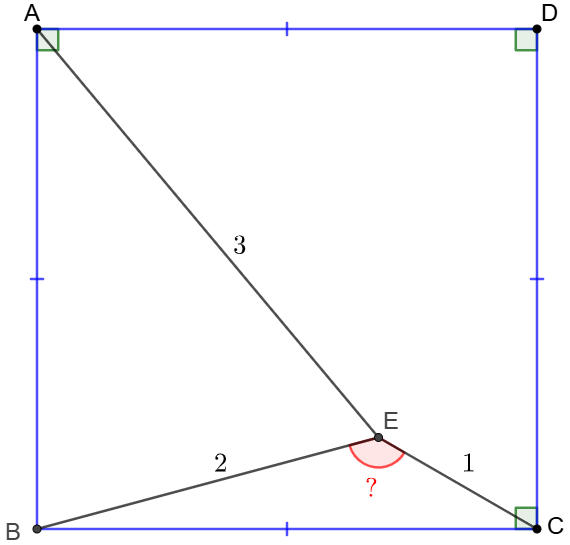
image-20250514001617324

Solve: \(\begin{multline} \shoveleft \text{Let }AB=BC=a \implies cos\angle{ABE}=\dfrac{a^2-5}{4a}=sin\angle{CBE}\\ \shoveleft cos\angle{CBE}=\dfrac{a^2+3}{4a} \implies (a^2+3)^2+(a^2-5)^2=16a^2\\ \shoveleft a^4-10a^2+17=0\implies a^2=5 + 2\sqrt{2} \text{ (abandon }5-2\sqrt{2})\\ \shoveleft \implies cos\angle{BEC}=\dfrac{5-(5+2\sqrt{2})}{4}=-\dfrac{\sqrt{2}}{2}\implies \angle{BEC}=\bbox[5px, border: 1px solid black]{135^{\circ}} \end{multline}\) Solve 2:

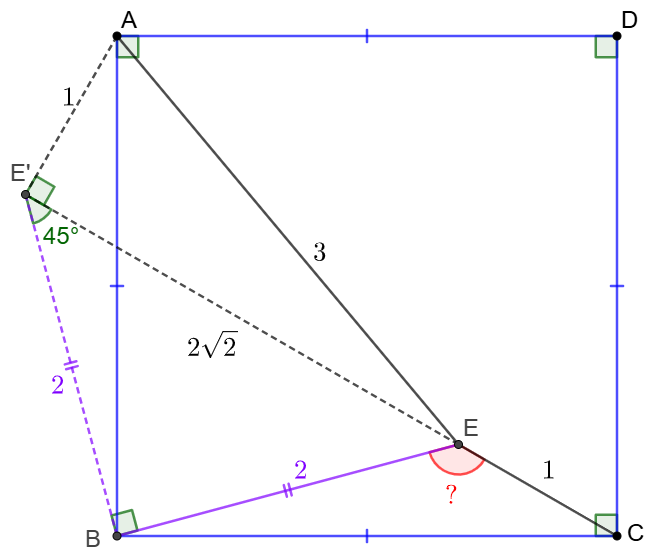image-20250514001521900 \(\begin{multline} \shoveleft \text{Make }BE'=BE, BE'\perp BE\implies \triangle{BCE}\cong\triangle{BAE'}\\ \shoveleft \implies EE'=2\sqrt{2},AE'=CE=1\\ \shoveleft \implies \angle{BE'E}=45^{\circ},AE'^2+EE'^2=AE^2\\ \shoveleft \implies \angle{AE'E}=90^{\circ}\implies \angle{AE'B}=\angle{BEC}=\bbox[5px, border: 1px solid black]{135^{\circ}} \end{multline}\)

05/22/2025

$D$ is a point inside $\triangle{ABC}$ where $\angle{ABC}=90^{\circ}$, $AD=\sqrt{3}$, $BC=\sqrt{2}$, $CD=1$, $\angle{ADC}=120^{\circ}$, find $\angle{BCD}$,

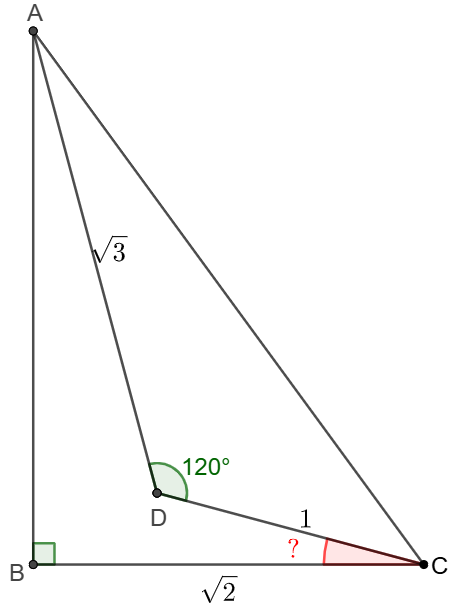
image-20250522005105810

Solve 1:

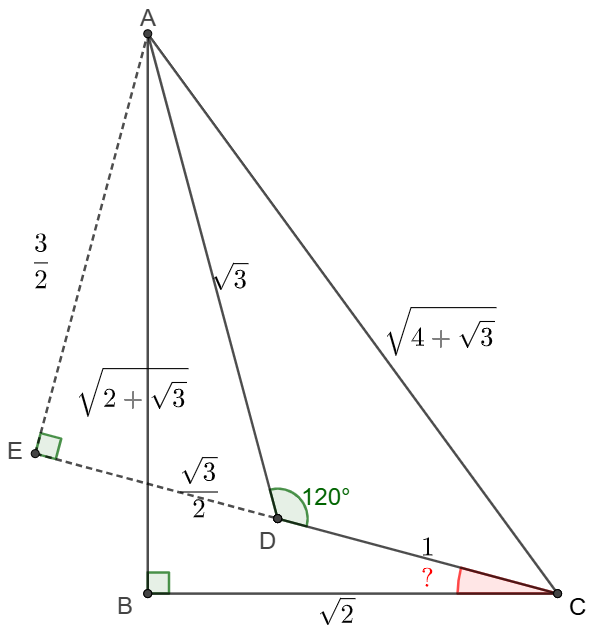image-20250522005554426 \(\begin{multline} \shoveleft AC=\sqrt{AD^2+CD^2-2\cdot AD\cdot CD \cdot cos\angle{ADC}}=\sqrt{4+\sqrt{3}}\\ \shoveleft \implies AB=\sqrt{AC^2-BC^2}=\sqrt{2+\sqrt{3}}\\ \shoveleft \text{Extend }CD \text{ to }E \text{ such that }AE\perp CE\\ \shoveleft \angle{ADC}=120^{\circ}\implies \angle{ADE}=60^{\circ}\\ \shoveleft \implies DE=\dfrac{AD}{2}=\dfrac{\sqrt{3}}{2}, AE=\dfrac{3}{2}\\ \end{multline}\)

05/25/2025

$ABCD$ is a square with side with $3$. $F$ is inside the square such that $\angle{AFC}=135^{\circ}$ and $E$ is the intersection of extended $CD$ and $BF$, $DE=1$, find $BF$.

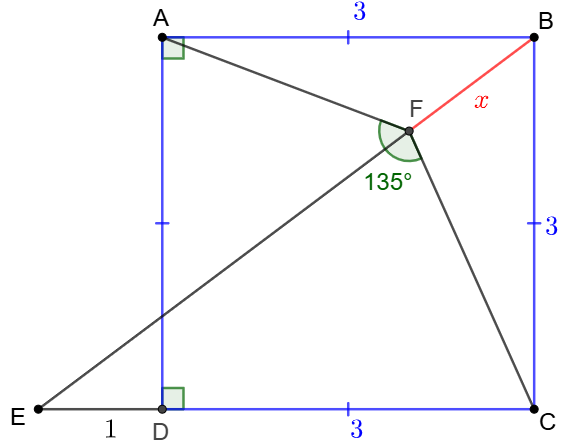
image-20250525001057761

Solve:

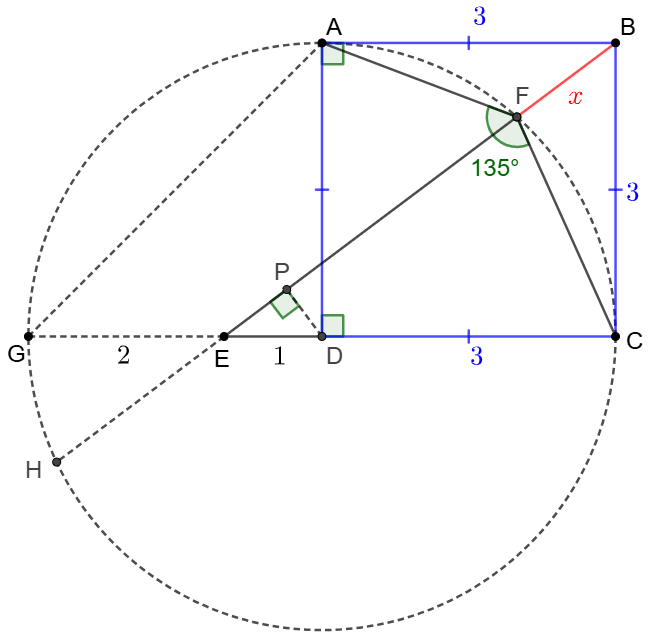image-20250525002423567 \(\begin{multline} \shoveleft \text{Extend }DE \text{ to } G \text{ such that }GE=2\implies \angle{AGC}=45^{\circ}\\ \shoveleft \implies AGCF \text{ is cyclic }\implies F \text{ is intersection of }\odot{GAFC} \cap BE\\ \shoveleft \text{Let }H \text{ be the meet of }\odot{GAFC} \text{ and extended } FE, PD\perp BE, BF=x\\ \shoveleft \implies \dfrac{PD}{DE}=\dfrac{BC}{BE}=\dfrac{3}{5}\implies PD=\dfrac{3}{5}\implies PF=\sqrt{9-\dfrac{9}{25}}=\dfrac{6\sqrt{6}}{5}\\ \shoveleft \implies BF\cdot BH=BC^2\implies x*(x+\dfrac{12\sqrt{6}}{5})=9\implies BF=x=\bbox[5px, border: 1px solid black]{\dfrac{21-6\sqrt{6}}{5}} \end{multline}\)

05/28/2025

$O$ is the center of eclipse $\dfrac{x^2}{80}+\dfrac{y^2}{50}=1$. $ABCD$ is a square with $A, D$ on the eclipse and $B, C$ on the axes of the eclipse. Find the area of $ABCD$.

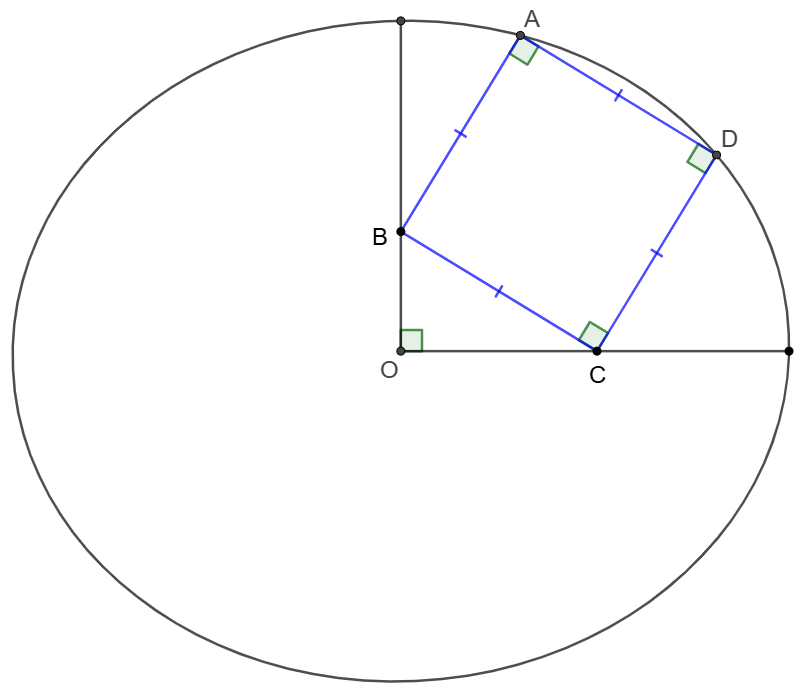
image-20250528020110366

Solve:

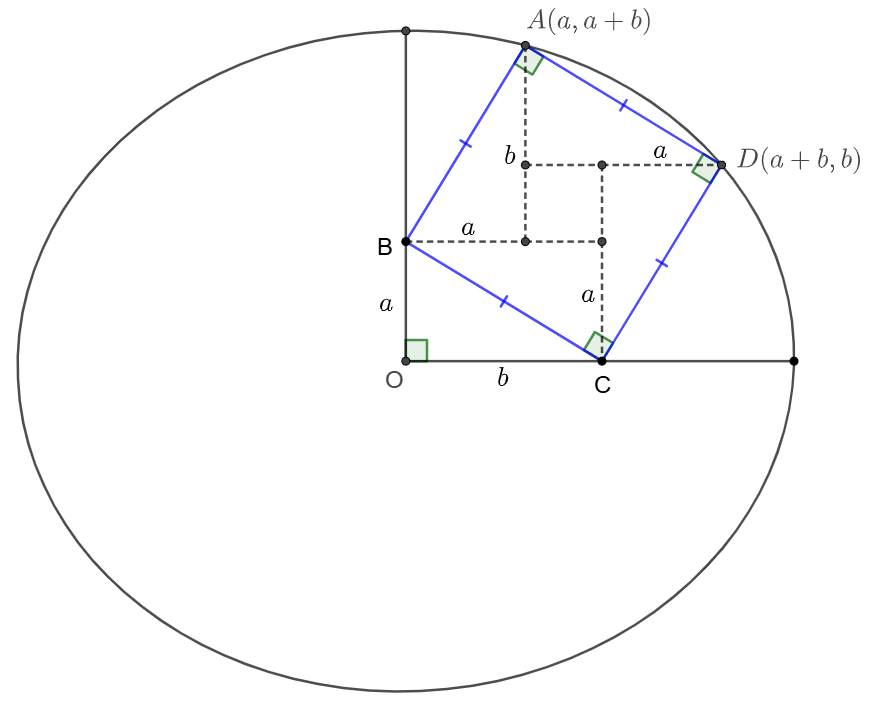image-20250528020833641 \(\begin{multline} \shoveleft \text{Let }BO=a, CO=b \implies A(a, a+b), D(a+b, b) \text{ on the eclipse}\\ \shoveleft \implies \dfrac{a^2}{80}+\dfrac{(a+b)^2}{50}=1, \dfrac{(a+b)^2}{80}+\dfrac{b^2}{50}=1 \implies 8a^2+6ab-5b^2=0\\ \shoveleft \implies a=\dfrac{b}{2}\implies b^2=\dfrac{1600}{77}\implies a^2+b^2=\dfrac{5}{4}b^2=\bbox[5px, border: 1px solid black]{\dfrac{2000}{77}} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search