M∀TH Workout

April 2025

 
  • Apr 01, 2025

04/11/2025

In circle $\odot{O}$ $AC=9, CD=4,DE=3, AC\perp CD, CD\perp DE$, find the radius of the circle.

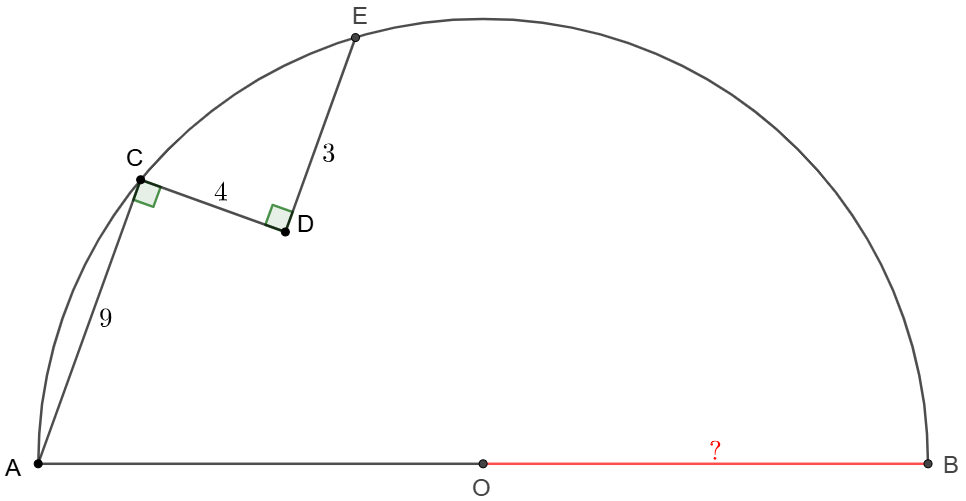
image-20250411205619557

Solve 1:

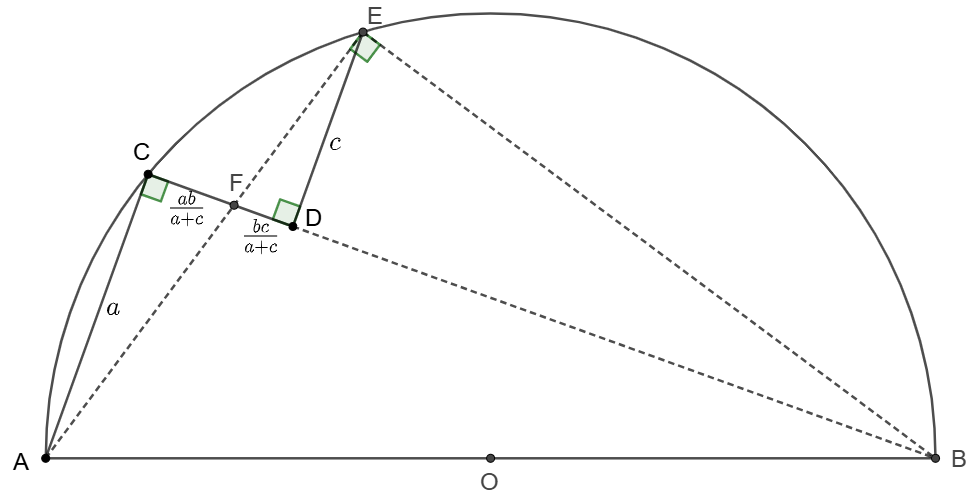image-20250411204022150 \(\begin{multline} \shoveleft \text{Let's make it general: }AC=a, CD=b, DE=c\\ \shoveleft \triangle{ACF}\sim\triangle{EDF}\implies \dfrac{CF}{DF}=\dfrac{AC}{DE}=\dfrac{a}{c}\implies CF=\dfrac{ab}{a+c}, DF=\dfrac{bc}{a+c}\\ \shoveleft \implies DE^2=DF \cdot BD\implies BD=\dfrac{c(a+c)}{b}\implies BC=\dfrac{b^2+c^2+ac}{b}\\ \shoveleft \implies AB^2=AC^2+BC^2=a^2+\Big(\dfrac{b^2+c^2+ac}{b}\Big)^2=a^2+\Big(b+\dfrac{c(a+c)}{b}\Big)^2\\ \shoveleft \implies AO=\dfrac{1}{2}\sqrt{a^2+\Big(b+\dfrac{c(a+c)}{b}\Big)^2}\implies AO=\bbox[5px, border: 1px solid black]{5\sqrt{10}} \end{multline}\) Solve 2:

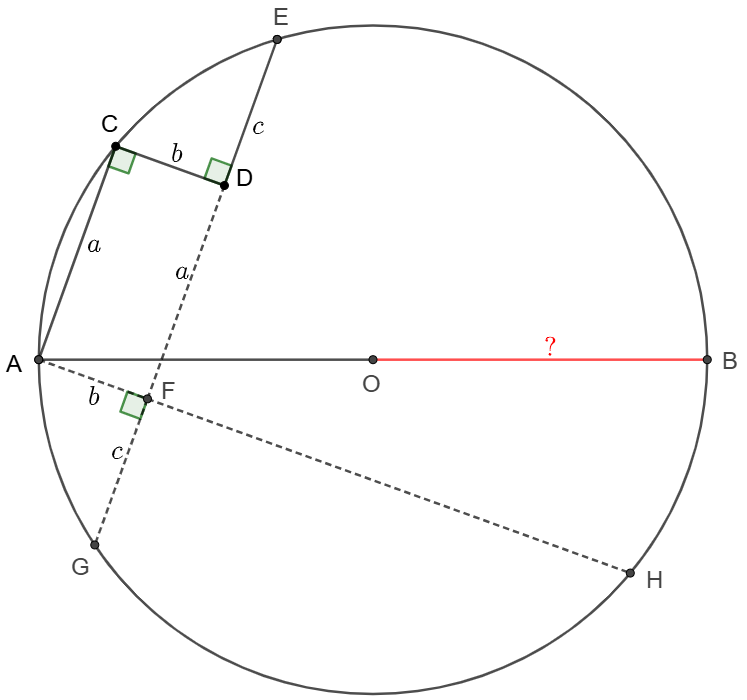image-20250411210210562 \(\begin{multline} \shoveleft \text{Let's make it general: }AC=a, CD=b, DE=c\\ \shoveleft \text{Extend }ED \text{ and intersect with }\odot{O} \text{ at }G\\ \shoveleft \text{make }AH\perp EG \text{ and }AH\cap EG=F, AH \cap \odot{O}=H\\ \shoveleft \implies DF=AC=a, AF=CD=b, FG=DE=c\\ \shoveleft \implies AF \cdot FH=EF \cdot FG \implies FH=\dfrac{c(a+c)}{b}\\ \shoveleft \implies 4\cdot AO^2=AF^2+FH^2+EF^2+FG^2\\ \shoveleft \implies AO=\dfrac{1}{2}\cdot\sqrt{(a+c)^2+b^2+c^2+\dfrac{c^2(a+c)^2}{b^2}}\\ \shoveleft \implies AO=\bbox[5px, border: 1px solid black]{5\sqrt{10}} \end{multline}\) Note: this is a quite often used theorem although no name: statement about orthogonal chords

04/17/2025

$ABCD$ is a square and $E$ is a point on the circle with $D$ as its center and $AD$ as its radius. The tangent line at $E$ intersects with $AB, BC$ at $F, G$ respectively. $MG \parallel CD, MG\cap AD=M, FN \parallel AD, FN\cap CD=N$. Prove that $[BFG]=[MDNK]$

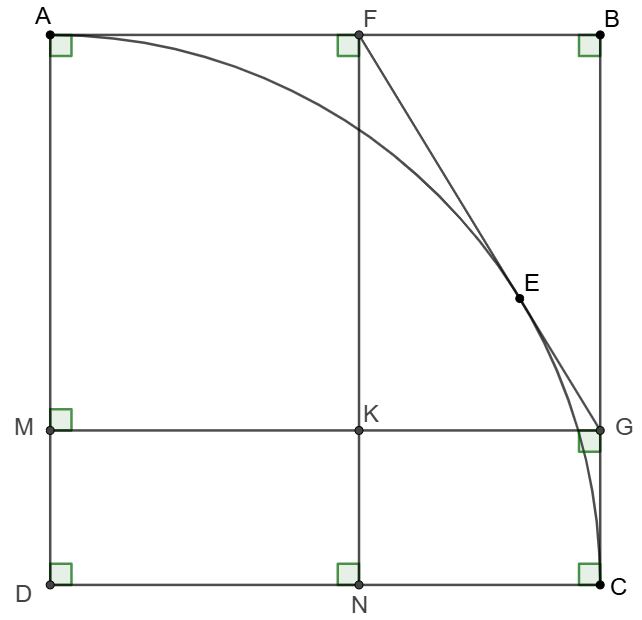
image-20250417163041818

Prove:

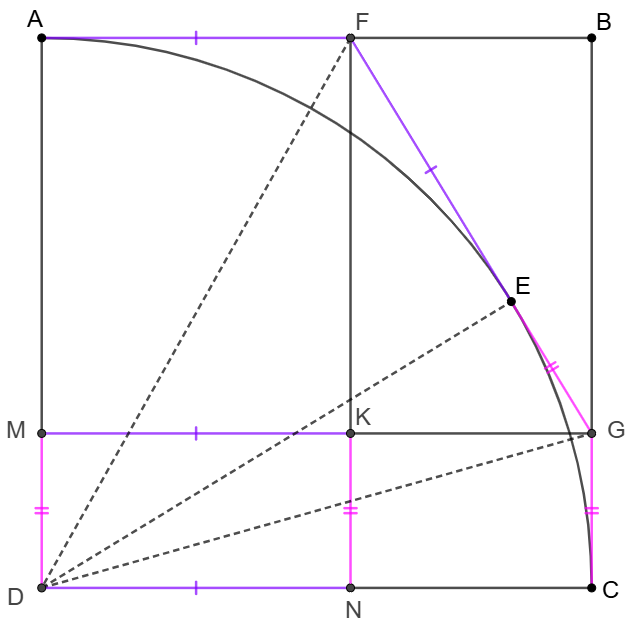image-20250417162306202 \(\begin{multline} \shoveleft \text{Connect }DE, DF, DG \implies DE\perp GF, FA=FE, GE=GC\\ \shoveleft \implies [DEF]=[ADF]=[DNF], [DEG]=[DCG]=[DMG]\\ \shoveleft \implies [ADEF]=[ADNF], [DCGE]=[DCGM]\\ \shoveleft \implies [ABCD]-[BFG]=[ADEF]+[DCGE]\\ \shoveleft =[ADNF]+[DCGM]=[ADNF]+[MDNK]+[KNCG]\\ \shoveleft \text{Since }[ABCD]-[BFG]=[ADNF]+[KNCG]+[FKG]\\ \shoveleft \implies [MDNK]=[FKG]=[BFG]\blacksquare \end{multline}\)

Prove 2:

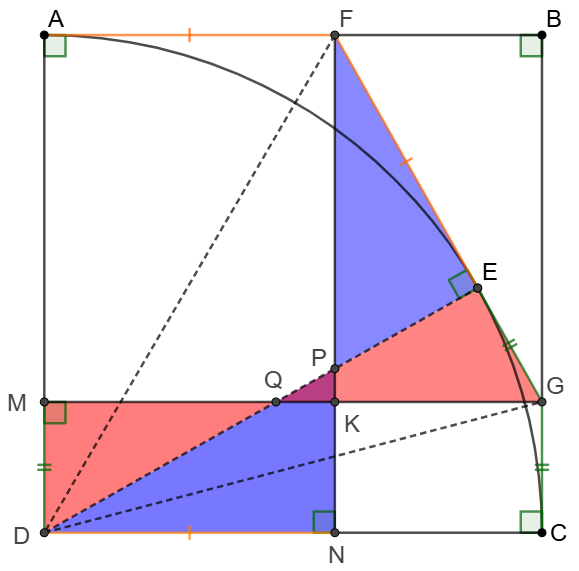image-20250418152739991 \(\begin{multline} \shoveleft \text{Let }FN\cap DE=P, MG\cap DE=Q\\ \shoveleft \text{Connect }DE, DF, DG \implies DE\perp GF, FA=FE=DN, GE=GC=DM\\ \shoveleft \implies [DEF]=[ADF]=[DNF], [DEG]=[DCG]=[DMG]\\ \shoveleft \implies [PEF]=[PDN]=[PQK]+[QDNK], [QDM]=[QEG]=[PQK]+[PKGE]\\ \shoveleft \implies [MDNK]=[QDM]+[QDNK]=[QDM]+[PDN]-[PQK]\\ \shoveleft =[QEG]+[PEF]-[PQK]=[PEF]+[PKGE]=[FKG]=[BFG]\blacksquare \end{multline}\)

04/26/2025

$a+b=1, a^2+b^2=2$, find $a^{11}+b^{11}$

Solve: \(\begin{multline} \shoveleft \href{https://en.wikipedia.org/wiki/Newton%27s_identities}{\text{Girard-Newton Identity}} \text{ and here is a video on } \href{https://www.youtube.com/watch?v=4FNCIYD8HdA}{\text{MindYourDecisions on Youtube}}\\ \shoveleft \text{so we know }p_1=1, p_2=2, e_0=1, e_1=p_1=1\\ \shoveleft \implies e_2=ab=p_2-2p_1^2=-\dfrac{1}{2}\\ \shoveleft \text{Or, } e_2=\dfrac{e_1p_1-e_0p_2}{2}=\dfrac{1-2}{2}=-\dfrac{1}{2}\\ \shoveleft e_i = 0 \text{ for }{i >= 3}\\ \shoveleft \implies e_3=\dfrac{1}{3}(e_2p_1-e_1p_2+e_3p_3)=0\implies p_3=\dfrac{5}{2}\\ \shoveleft \implies e_4=-\dfrac{1}{4}(e_2p_2-e_1p_3+e_0p_4) = 0 \implies p_4=\dfrac{7}{2}\\ \shoveleft \implies e_5=\dfrac{1}{5}(e_2p_3-e_1p_4+e_0p_5)=0\implies p_5=\dfrac{19}{4}\\ \shoveleft \implies e_6=-\dfrac{1}{6}(e_2p_4-e_1p_5+e_0p_6)=0 \implies p_6=\dfrac{13}{7}\\ \shoveleft \implies e_7=\dfrac{1}{7}(e_2p_5-e_1p_6+e_0p_7)=0 \implies p_7=\dfrac{71}{8}\\ \shoveleft \implies e_8=-\dfrac{1}{8}(e_2p_6-e_1p_7+e_0p_8)=0 \implies p_8=\dfrac{97}{8}\\ \shoveleft \implies e_9=\dfrac{1}{9}(e_2p_7-e_1p_8+e_0p_9)=0 \implies p_9=\dfrac{265}{16}\\ \shoveleft \implies e_10=-\dfrac{1}{10}(e_2p_8-e_1p_9+e_0p_{10})=0\implies p_{10}=\dfrac{181}{8}\\ \shoveleft \implies e_{11}=\dfrac{1}{11}(e_2p9-e_1p_{10}+e_0p_{11})=0 \implies p_{11}=a^{11}+b^{11}=\bbox[5px, border: 1px solid black]{\dfrac{989}{32}} \end{multline}\)

4/27/2025

$CD, EF$ are chords on semicircle with $AB$ as its diameter. $CD=16, EF=8. DF, CE$ are extended and meet at $G$, $FG\perp EG$, find $AB$.

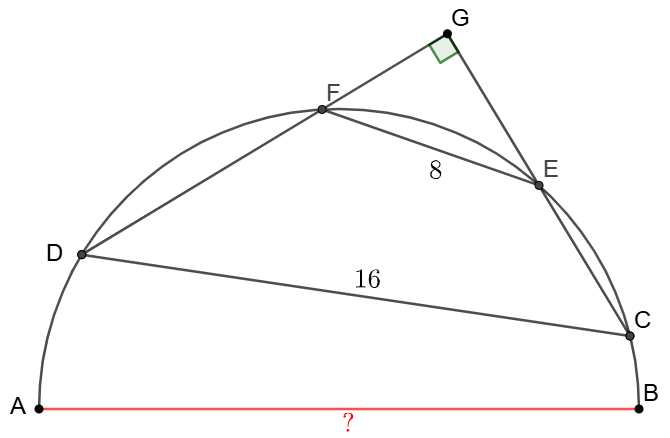
image-20250427145555157

Solve 1:

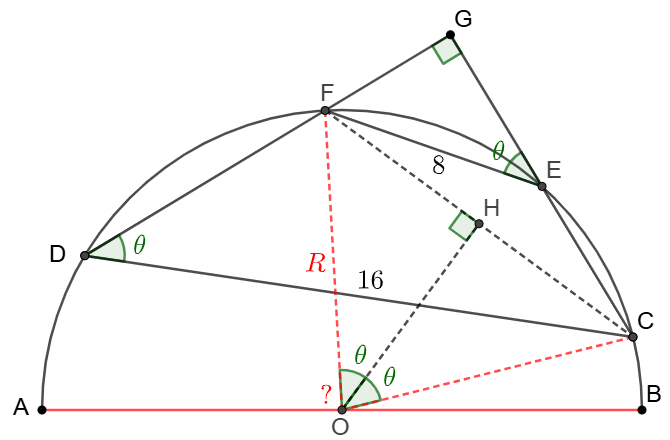image-20250427210017848 \(\begin{multline} \shoveleft \text{Connect }CF \text{ and let }H \text{ on }CF \text{ such that }OH\perp CF\\ \shoveleft \text{Let }\angle{FEG}=\angle{CDF}=\theta \implies \angle{COF}=2\theta\implies \angle{FOH}=\theta\\ \shoveleft \text{Suppose }CD=a, EF=b \implies \\ \shoveleft EG=bcos\theta, FG=bsin\theta,DG=acos\theta, CG=asin\theta\\ \shoveleft \implies CF=\sqrt{a^2+b^2}sin\theta\implies FH=\dfrac{\sqrt{a^2+b^2}}{2}sin\theta\\ \shoveleft \implies R=\dfrac{FH}{sin\theta}=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{a^2+b^2}}{2}}. \text{ When }a=16,b=8, R=\bbox[5px, border: 1px solid black]{4\sqrt{5}} \end{multline}\)

Solve 2:

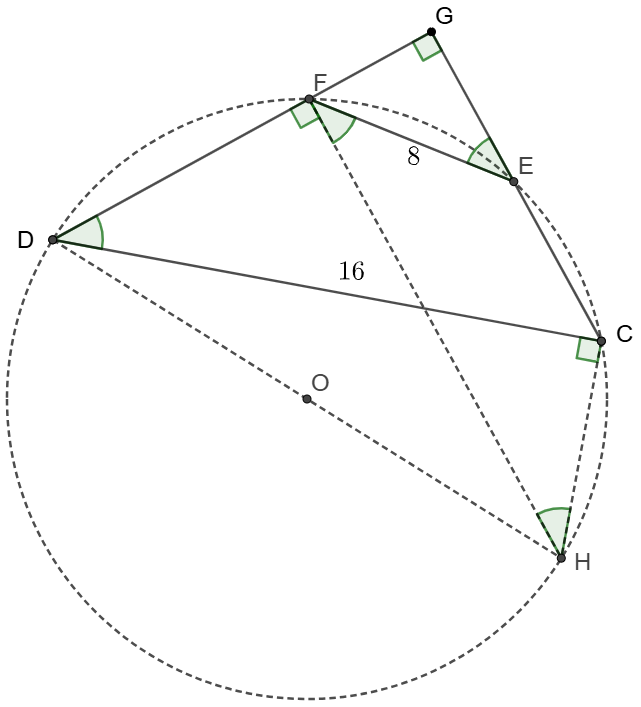image-20250427222943496 \(\begin{multline} \shoveleft \text{Suppose }CD=a, EF=b, \text{the radius of }\odot{CDFE} \text{ is }R\\ \shoveleft \text{Let }O \text{ be the center of }\odot{CDFE}, DH \text{ be the diamete}\\ \shoveleft \implies \angle{DFH}=\angle{DCH}=\angle{DGC}=90^{\circ}\implies FH\parallel CG\\ \shoveleft \implies \angle{FEG}=\angle{EFH}=\angle{CDG}=\angle{CHF}\\ \shoveleft \implies CHFE \text{ is an isosceles trapezoid }\implies CH=EF=b\\ \shoveleft \implies DH^2=4R^2=CD^2+CH^2=a^2+b^2\\ \shoveleft \implies R=\dfrac{FH}{sin\theta}=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{a^2+b^2}}{2}}. \text{ When }a=16,b=8, R=\bbox[5px, border: 1px solid black]{4\sqrt{5}} \end{multline}\)

Solve 3:

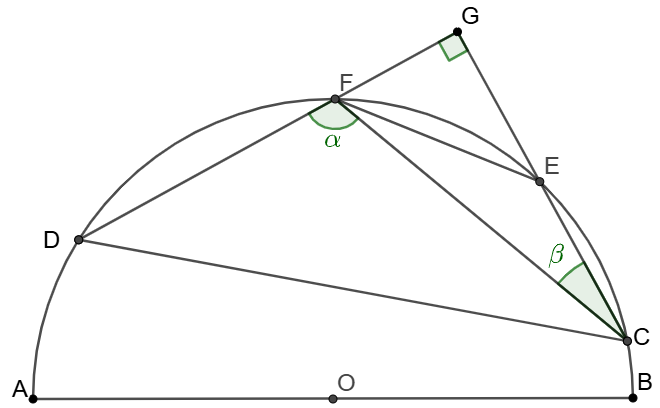image-20250428155027489 \(\begin{multline} \shoveleft \text{Let the radius of }\odot{CDFE} \text{ is }R, \angle{ECF}=\beta, \angle{CFD}=\alpha\\ \shoveleft \implies \alpha=90^{\circ}+\beta \implies \dfrac{CD}{sin\alpha}=\dfrac{EF}{sin\beta}=2R\\ \shoveleft \implies \dfrac{a}{sin(90^{\circ}+\beta)}=\dfrac{a}{cos\beta}=\dfrac{b}{sin\beta}=2R\\ \shoveleft \implies a^2+b^2=4R^2\implies R=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{a^2+b^2}}{2}}\\ \shoveleft \text{ When }a=16,b=8, R=\bbox[5px, border: 1px solid black]{4\sqrt{5}} \end{multline}\)

04/30/2025

$T,B,C$ are points on circle such that $\overset{\huge\frown}{TB}=\overset{\huge\frown}{TC}$. $A$ is a point on $\overset{\huge\frown}{TC}$. The angle bisector of $\angle{ABC}$ meets the circle at $M$ and the angle bisector of $\angle{ACB}$ meets $AB$ at $D$. Extend $TA$ and $DM$ to meet at $N$. Prove that $BM \parallel CN$.

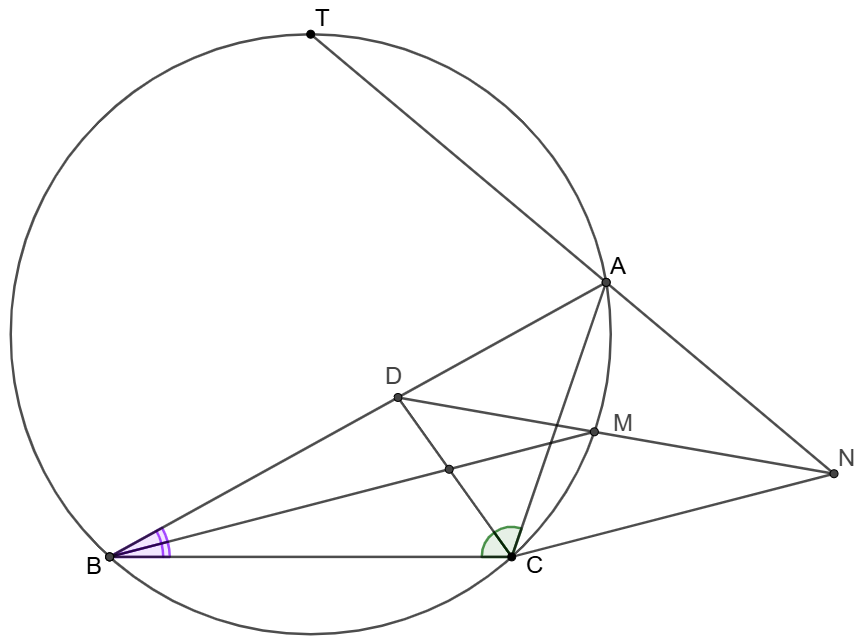
image-20250430233516002

Prove:

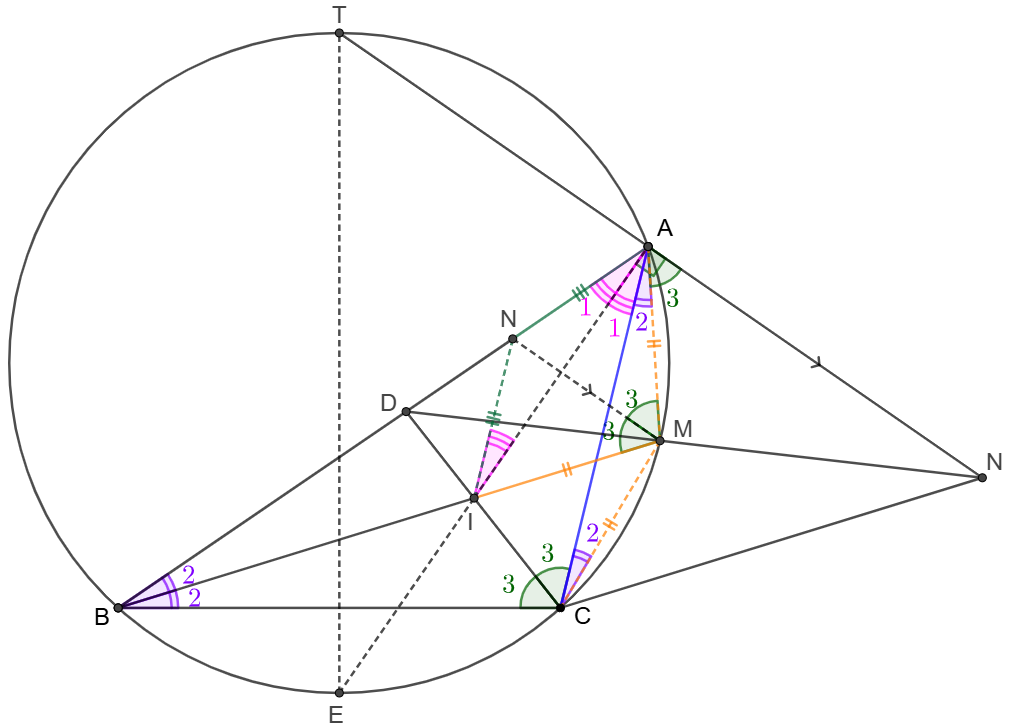image-20250501000805925 \(\begin{multline} \shoveleft \text{Let }I=BM\cap CD \implies I \text{ is the incenter of }\triangle{ABC} \implies \angle{BAI}=\angle{IAC}\\ \shoveleft \text{Let }\angle{BAI}=\angle{IAC}=\angle{1}, \angle{ABI}=\angle{IBC}=\angle{2}, \angle{BCI}=\angle{ICA}=\angle{3}\\ \shoveleft \implies \angle{CAM}=\angle{ACM}=\angle{2}\implies AM=CM\\ \shoveleft \angle{MIC}=\angle{2}+\angle{3}=\angle{MCI}\implies CM=IM\\ \shoveleft \implies M\text{ is circumcenter of }\triangle{AIC}\implies \angle{AMI}=2\angle{3}\\ \shoveleft \text{Let extended }AI \text{ meets the circle at }E \implies \overset{\huge\frown}{BE}=\overset{\huge\frown}{CE}\implies BE=CE\\ \shoveleft TB=TC \implies \triangle{TBE}\cong\triangle{TCE}\implies \angle{TCE}=\angle{TBE}=90^{\circ}=\angle{TAE}\\ \shoveleft \implies \angle{MAN}=90^{\circ}-\angle{1}-\angle{2}=\angle{3}\\ \shoveleft \text{Let the bisector of }\angle{AMI} \text{ meet }AB \text{ at }N \implies \angle{AMN}=\angle{IMN}=\angle{3}=\angle{MAN}\\ \shoveleft \implies MN \parallel AN, \triangle{AMN}\cong\triangle{IMN}\implies AN=NI\implies \angle{NIA}=\angle{NAI}=\angle{IAC}\\ \shoveleft \implies NI \parallel AC\implies \dfrac{DI}{IC}=\dfrac{DN}{NA}=\dfrac{DM}{MN}\implies BM \parallel CN\blacksquare \end{multline}\)

    © M∀TH Workout 2020-2021
    Search