03/11/2025
$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=\angle{CBD}=20^{\circ}, \angle{BAD}=30^{\circ}, \angle{CAD}=80^{\circ}$, find $\angle{BCD}$
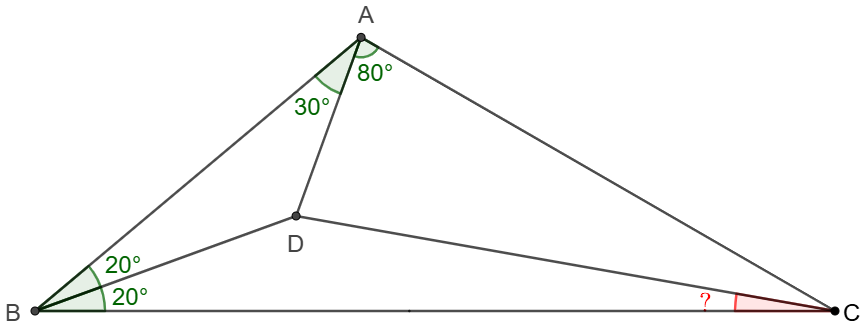
Solve:
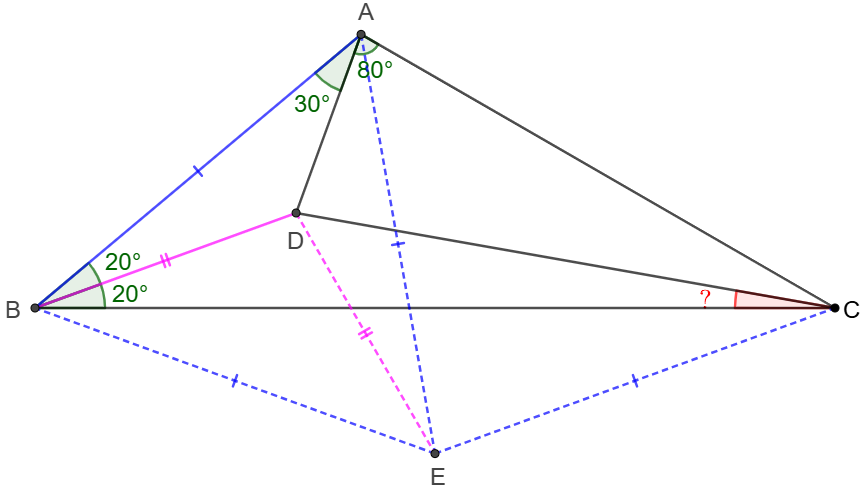 \(\begin{multline}
\shoveleft \angle{BAC}=110^{\circ}, \angle{ABC}=40^{\circ}\implies \angle{ACB}=30^{\circ}\\
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC} \\
\shoveleft \implies AE=BE=CE, \angle{AEB}=2\angle{ACB}=60^{\circ}\\
\shoveleft \implies \triangle{ABE}\text{ is equilateral} \implies \angle{ABE}=\angle{BAE}=60^{\circ} \\
\shoveleft \implies \angle{EAD}=\angle{BAD}=30^{\circ},\angle{EBC}=\angle{BCE}=20^{\circ}\\
\shoveleft \implies \triangle{ABD}\cong\triangle{AED}\implies \angle{ADE}=\angle{ADB}=130^{\circ}\\
\shoveleft \implies \angle{ADB}+\angle{ACE}=130^{\circ}+30^{\circ}+20^{\circ}=180^{\circ}\\
\shoveleft \implies ACED\text{ are cyclic }\implies \angle{DCE}=\angle{DAE}=30^{\circ}\\
\shoveleft \implies \angle{DCB}=30^{\circ}-20^{\circ}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \angle{BAC}=110^{\circ}, \angle{ABC}=40^{\circ}\implies \angle{ACB}=30^{\circ}\\
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC} \\
\shoveleft \implies AE=BE=CE, \angle{AEB}=2\angle{ACB}=60^{\circ}\\
\shoveleft \implies \triangle{ABE}\text{ is equilateral} \implies \angle{ABE}=\angle{BAE}=60^{\circ} \\
\shoveleft \implies \angle{EAD}=\angle{BAD}=30^{\circ},\angle{EBC}=\angle{BCE}=20^{\circ}\\
\shoveleft \implies \triangle{ABD}\cong\triangle{AED}\implies \angle{ADE}=\angle{ADB}=130^{\circ}\\
\shoveleft \implies \angle{ADB}+\angle{ACE}=130^{\circ}+30^{\circ}+20^{\circ}=180^{\circ}\\
\shoveleft \implies ACED\text{ are cyclic }\implies \angle{DCE}=\angle{DAE}=30^{\circ}\\
\shoveleft \implies \angle{DCB}=30^{\circ}-20^{\circ}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
03/26/2025
$ABCD$ is a square with side length $1$. $E$ is on extended $DC$. $BC$ and $AE$ intersect at $F$. $EF=1$, find $CE$.
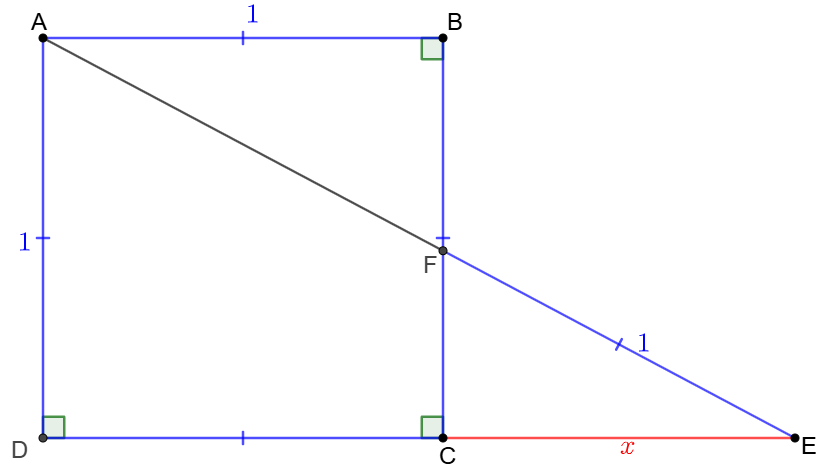
Solve 1: \(\begin{multline} \shoveleft \dfrac{CF}{CE}=\dfrac{AD}{DE}\implies CF=\dfrac{x}{1+x}\\ \shoveleft \implies CE^2+CF^2=1\implies x^2+(\dfrac{x}{1+x})^2=1\\ \shoveleft \text{Let }x=sin\theta \implies cos\theta=\dfrac{x}{1+x}\\ \shoveleft \implies cos\theta = \dfrac{sin\theta}{1+sin\theta}\\ \shoveleft \implies sin\theta \cdot cos\theta=sin\theta - cos\theta\\ \shoveleft \implies sin2\theta=2(sin\theta-cos\theta)\\ \shoveleft \implies sin^22\theta=4(1-2\cdot sin\theta \cdot cos\theta)=4(1-sin2\theta)\\ \shoveleft sin^22\theta+4sin2\theta-4=0\implies sin2\theta=-2\pm\sqrt{2}\\ \shoveleft \implies sin\theta \cdot cos\theta=-1\pm\sqrt{2}=\dfrac{x^2}{1+x}\\ \shoveleft \implies x^2+(1\pm\sqrt{2})x+(1\pm\sqrt{2})=0 \text{ and x must be positive real}\\ \shoveleft \implies x^2 + (1-\sqrt{2})x +(1-\sqrt{2})=0\\ \shoveleft \implies x=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}} \end{multline}\) Solve 2: \(\begin{multline} \shoveleft \dfrac{CF}{CE}=\dfrac{AD}{DE}\implies CF=\dfrac{x}{1+x}\\ \shoveleft \implies CE^2+CF^2=1\implies x^2+(\dfrac{x}{1+x})^2=1\\ \shoveleft \text{Let }t=x+1>0 \implies (t-1)^2+(\dfrac{t-1}{t})^2=1\\ \shoveleft \implies (t-1)^2+(\dfrac{1}{t}-1)^2=1\\ \shoveleft \implies t^2-2t+1+(\dfrac{1}{t})^2-\dfrac{2}{t}+1=1\\ \shoveleft \implies (t+\dfrac{1}{t})^2-2(t+\dfrac{1}{t})+1=2\\ \shoveleft \implies t+\dfrac{1}{t}=1+\sqrt{2}\implies t=\dfrac{1+\sqrt{2}+\sqrt{2\sqrt{2}-1}}{2}\\ \shoveleft \implies x=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}} \end{multline}\) Solve 3: \(\begin{multline} \shoveleft \dfrac{CF}{CE}=\dfrac{AD}{DE}\implies CF=\dfrac{x}{1+x}, x>0\\ \shoveleft \implies CE^2+CF^2=1\implies x^2+(\dfrac{x}{1+x})^2=1\\ \shoveleft \implies x^2+(1-\dfrac{1}{x+1})^2=1\\ \shoveleft \implies x^2+(\dfrac{1}{x+1})^2-\dfrac{2}{x+1}+1=1\\ \shoveleft \implies (x+\dfrac{1}{x+1})^2-\dfrac{2x}{x+1}-\dfrac{2}{x+1}+1=1\\ \shoveleft \implies (x+\dfrac{1}{x+1})^2=2\implies x+\dfrac{1}{x+1}=\sqrt{2}\\ \shoveleft \implies x^2+(1-\sqrt{2})x+1-\sqrt{2}=0\\ \shoveleft \implies x=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}} \end{multline}\)
Solve 4:
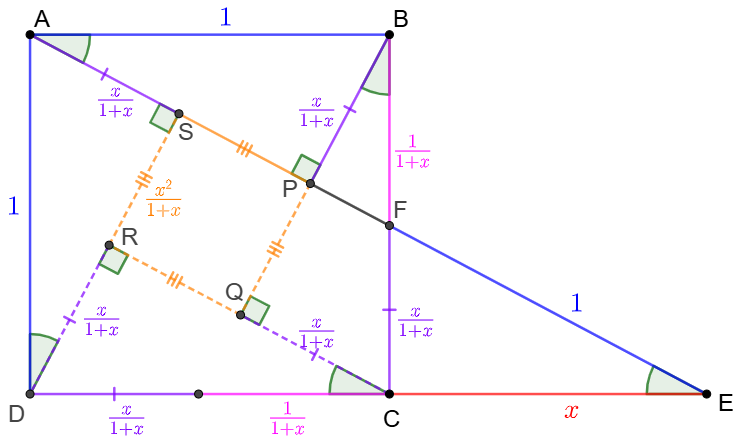 \(\begin{multline}
\shoveleft \dfrac{CF}{CE}=\dfrac{AD}{DE}\implies CF=\dfrac{x}{1+x}, x>0\\
\shoveleft \text{Make }\triangle{APB}\cong\triangle{BQC}\cong\triangle{CRD}\cong\triangle{DSA}\cong\triangle{ECF}\\
\shoveleft \implies CF=AS=BP=CQ=DR=\dfrac{x}{1+x}\\
\shoveleft \implies PQ=QR=RS=SP=x-\dfrac{x}{1+x}=\dfrac{x^2}{1+x}\\
\shoveleft \implies 4[ECF]+[PQRS]=1\implies 4\dfrac{x^2}{2(1+x)}+\Big(\dfrac{x^2}{(1+x)}\Big)^2=1\\
\shoveleft \implies \Big(\dfrac{x^2}{1+x}+1\Big)^2=2\implies \dfrac{x^2}{1+x}=\sqrt{2}-1\\
\shoveleft \implies x=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}}
\end{multline}\)
\(\begin{multline}
\shoveleft \dfrac{CF}{CE}=\dfrac{AD}{DE}\implies CF=\dfrac{x}{1+x}, x>0\\
\shoveleft \text{Make }\triangle{APB}\cong\triangle{BQC}\cong\triangle{CRD}\cong\triangle{DSA}\cong\triangle{ECF}\\
\shoveleft \implies CF=AS=BP=CQ=DR=\dfrac{x}{1+x}\\
\shoveleft \implies PQ=QR=RS=SP=x-\dfrac{x}{1+x}=\dfrac{x^2}{1+x}\\
\shoveleft \implies 4[ECF]+[PQRS]=1\implies 4\dfrac{x^2}{2(1+x)}+\Big(\dfrac{x^2}{(1+x)}\Big)^2=1\\
\shoveleft \implies \Big(\dfrac{x^2}{1+x}+1\Big)^2=2\implies \dfrac{x^2}{1+x}=\sqrt{2}-1\\
\shoveleft \implies x=\bbox[5px, border: 1px solid black]{\dfrac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}}
\end{multline}\)
03/31/2025
Fold semicircle $AB$ along its chord $CD$ so that it is tangent to $AB$ at $E$. $CD=K, AE=a, BE=b$, show that $K=\sqrt{\dfrac{a^2+4ab+b^2}{2}}$
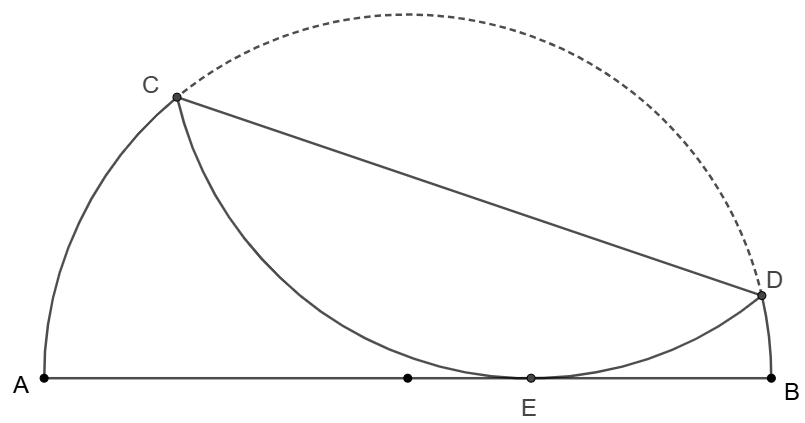
Prove:
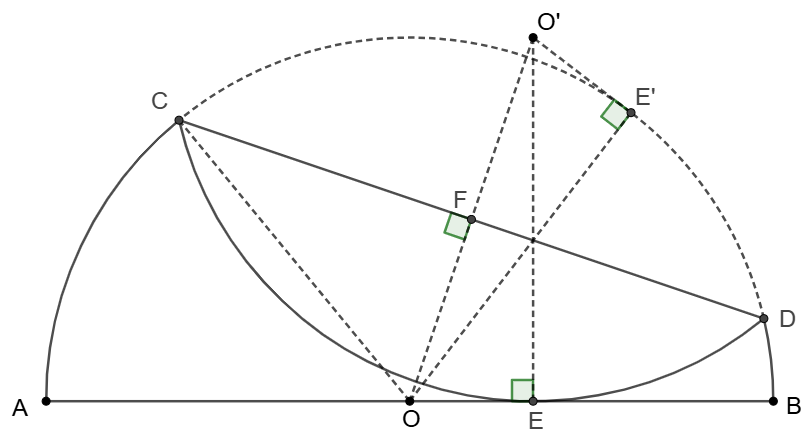 \(\begin{multline}
\shoveleft \text{Suppose }a>b, \text{Let }O \text{ be the center of semicircle }AB\\
\shoveleft \text{Let }AO=BO=R, AE=a=R+OE, BE=b=R-OE\\
\shoveleft \implies OE=\dfrac{a-b}{2}, R=\dfrac{a+b}{2} \\
\shoveleft \text{Make }O', E' \text{ be the mirror points of }O, E \text{ along } CD\\
\shoveleft \implies OE]=O'E=R, O'E\perp AB\\
\shoveleft \implies O'O^2=OE^2+O'E^2=(\dfrac{a+b}{2})^2+(\dfrac{a-b}{2})^2=\dfrac{a^2+b^2}{2}\\
\shoveleft \text{Let }CD\cap OO'=F\\
\shoveleft \implies OF=\dfrac{OO'}{2},CO=R=\dfrac{a+b}{2}, CF=\dfrac{CD}{2}=\dfrac{K}{2}\\
\shoveleft \implies CF^2=CO^2-OF^2=(\dfrac{a+b}{2})^2-(\dfrac{a^2+b^2}{8})=\dfrac{a^2+4ab+b^2}{8}\\
\shoveleft \implies CD=K=2CF=\sqrt{\dfrac{a^2+4ab+b^2}{2}}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Suppose }a>b, \text{Let }O \text{ be the center of semicircle }AB\\
\shoveleft \text{Let }AO=BO=R, AE=a=R+OE, BE=b=R-OE\\
\shoveleft \implies OE=\dfrac{a-b}{2}, R=\dfrac{a+b}{2} \\
\shoveleft \text{Make }O', E' \text{ be the mirror points of }O, E \text{ along } CD\\
\shoveleft \implies OE]=O'E=R, O'E\perp AB\\
\shoveleft \implies O'O^2=OE^2+O'E^2=(\dfrac{a+b}{2})^2+(\dfrac{a-b}{2})^2=\dfrac{a^2+b^2}{2}\\
\shoveleft \text{Let }CD\cap OO'=F\\
\shoveleft \implies OF=\dfrac{OO'}{2},CO=R=\dfrac{a+b}{2}, CF=\dfrac{CD}{2}=\dfrac{K}{2}\\
\shoveleft \implies CF^2=CO^2-OF^2=(\dfrac{a+b}{2})^2-(\dfrac{a^2+b^2}{8})=\dfrac{a^2+4ab+b^2}{8}\\
\shoveleft \implies CD=K=2CF=\sqrt{\dfrac{a^2+4ab+b^2}{2}}\blacksquare
\end{multline}\)