02/21/2025

$AB, CD$ are perpendicular chords inside circle $\odot{O}$. $AC=30, BD=40$. Find the radius of $\odot{O}$.

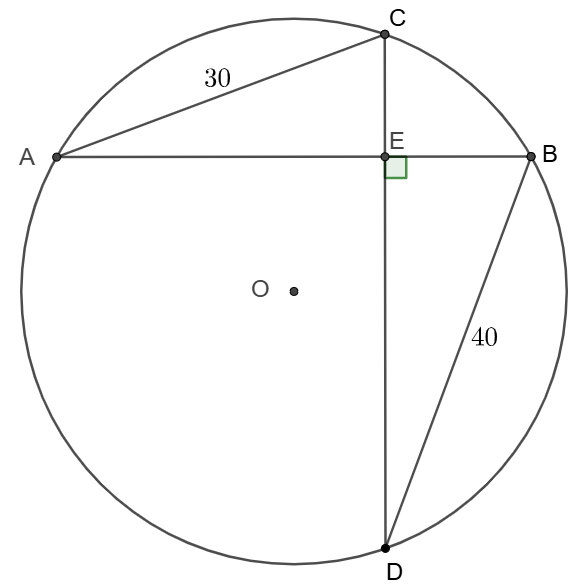
Solve:

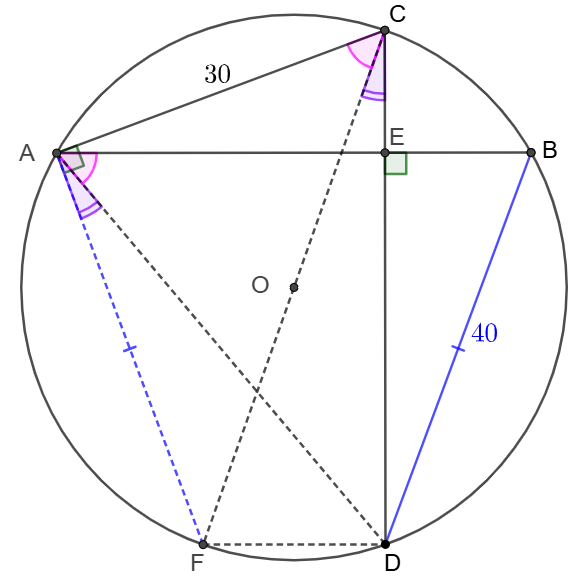\(\begin{multline} \shoveleft \text{Let }CF \text{ to be the diameter of }\odot{O} \implies \angle{CAF}=90^{\circ}\\ \shoveleft \implies \angle{CAE}+\angle{ACE}=\angle{CAE}+\angle{FAE}=90^{\circ}\\ \shoveleft \implies \angle{ACE}=\angle{FAE}\implies \angle{ACF}+\angle{DCF}=\angle{DAF}+\angle{DAB}\\ \shoveleft \text{Since }\angle{DAF}=\angle{DCF}\implies \angle{ACF}=\angle{DAB}\implies AF=BF\\ \shoveleft \implies CF^2=AC^2+AF^2=30^2+40^2=50^2\implies CF=50\\ \shoveleft \implies 2R=50\implies R=\bbox[5px, border: 1px solid black]{25} \end{multline}\) Note: If the intersection of any two perpendicular chords divides one chord into lengths $a$ and $b$ and divides the other chord into lengths $c$ and $d$, then $a^2+b^2+c^2+d^2$ equals to the square of the diameter. This is shown here