M∀TH Workout

January 2025

 
  • Jan 04, 2025

01/04/2025

Circles $\odot{O_1}, \odot{O_2}$ are of the same radius $r_1$. Circles $\odot{O_3}, \odot{O_4}$ are of the same radius $r_2$. They are tangent and inscribed inside semi-circle $\odot{O}$ of radius $r$ and its diameter $AB$ and chord $BC$. If $r_1, r_2 $ and $r$ are all integers, find the minimum value of $r$.

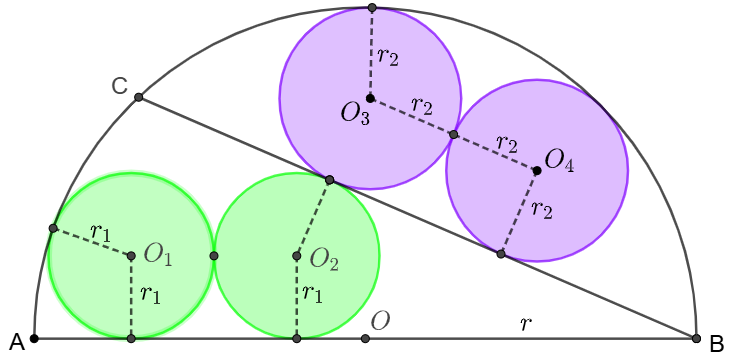
image-20250104185143876

Solve:

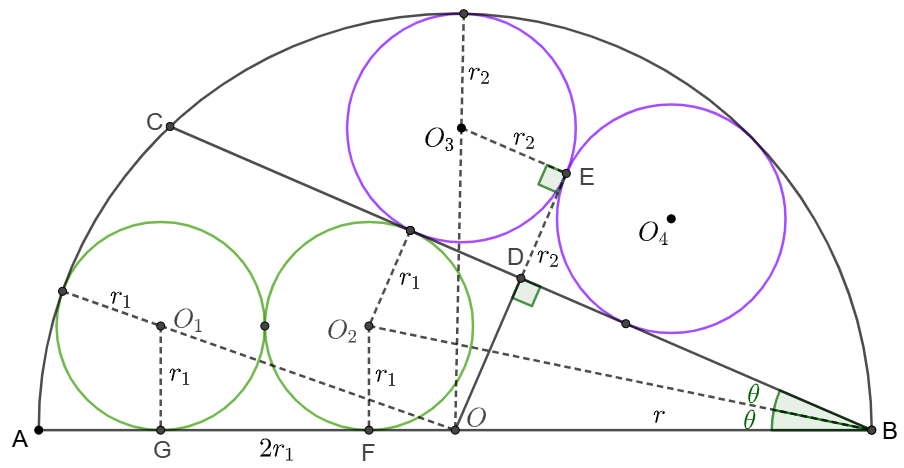image-20250104200809598 \(\begin{multline} \shoveleft \text{Let }m=\dfrac{r_1}{r}, n=\dfrac{r_2}{r} \implies m,n \text{ are rational numbers}, m,n \lt \dfrac{1}{2}\\ \shoveleft OO_1=r-r_1 \implies GO=\sqrt{(r-r_1)^2-r_1^2}, GF=2r_1\\ \shoveleft \implies FO=\sqrt{(r-r_1)^2-r_1^2}-2r_1 = \sqrt{r^2-2rr_1} -2r_1\\ \shoveleft \implies FB=r-2r_1+\sqrt{r^2-2rr_1}\\ \shoveleft \implies tan \theta = \dfrac{r_1}{r-2r_1+\sqrt{r^2-2rr_1}}=\dfrac{m}{1-2m+\sqrt{1-2m}}\\ \shoveleft =\dfrac{1}{2}(\dfrac{1}{\sqrt{1-2m}}-1)\\ \shoveleft OO_3=r-r_2 \implies EO=\sqrt{(r-r_2)^2-r_2^2}, DE=r_2\\ \shoveleft \implies DO=EO-DE=\sqrt{(r-r_2)^2-r_2^2}-r_2=\sqrt{r^2-2rr_2}-r_2\\ \shoveleft \implies sin2\theta=\dfrac{DO}{BO}=\dfrac{\sqrt{(r-r_2)^2-r_2^2}-r_2}{r}=\sqrt{1-2n}-n\\ \shoveleft \implies \sqrt{1-2n}-n=\dfrac{2 \cdot tan\theta}{1+tan^2\theta}=\dfrac{\dfrac{1}{\sqrt{1-2m}}-1}{1+\dfrac{1}{4}(\dfrac{1}{\sqrt{1-2m}}-1)^2}\\ \shoveleft =\dfrac{-20m^2+18m-4+(4-6m)\sqrt{1-2m}}{(3-5m)^2-4(1-2m)}\\ \shoveleft \text{If }\sqrt{1-2m} \text{ is irrational number, then we will have }\sqrt{1-2n}=s+t\sqrt{u}\\ \shoveleft \text{where }u \text{ is an integer of non perfect square}, s, t\text{ are rational numbers}.\\ \shoveleft \text{But }1-2n=s^2+t^2u + 2st\sqrt{u} \text{ is a rational number while }\sqrt{u} \text{ is irrational}\\ \shoveleft \implies st=0 \implies s=0 \text{ or } t=0\\ \shoveleft m<\dfrac{1}{2} \implies (3-5m)^2-4(1-2m)>0, 4-6m>0 \implies t>0\implies s=0\\ \shoveleft \implies s=n+\dfrac{-20m^2+18m-4}{(3-5m)^2-4(1-2m)}=0\implies n=\dfrac{20m^2-18m+4}{(3-5m)^2-4(1-2m)}\\ \shoveleft \text{and }\sqrt{1-2n}=\dfrac{(4-6m)\sqrt{1-2m}}{(3-5m)^2-4(1-2m)}\implies \end{multline}\)

01/20/2025

The radius of the circumcircle of $\triangle{ABC}$ is $14$, $AB=4, AC=7, AD\perp BC$, find $AD$.

Solve:

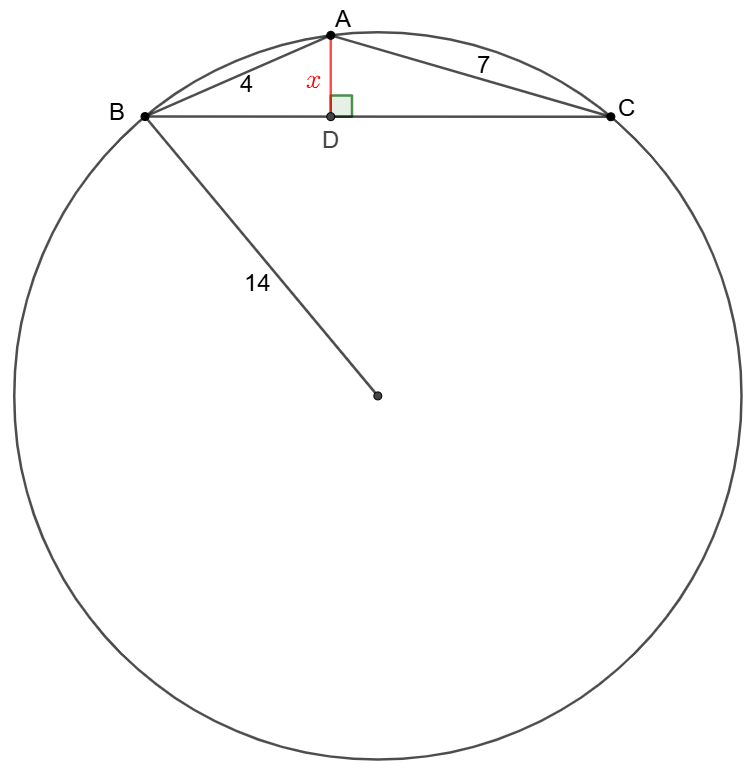image-20250121044103088 \(\begin{multline} \shoveleft \text{Via the Law of Sines } \dfrac{AB}{sin\angle{ACB}}=2R\\ \shoveleft \implies \dfrac{AB}{\dfrac{AD}{AC}}=2 * 14=28\\ \shoveleft \implies AD=\dfrac{AB * AC}{28}=\bbox[5px, border: 1px solid black]{1} \end{multline}\)

01/21/2025

$\triangle{ABC}$ is a right triangle. Take $AB,AC,BC$ as diameters to get three circles and form $S_1, S_2, S_3, S_4$ as shown below. Prove that $[ABC]=S_1+S_2=S_4-S_3$.

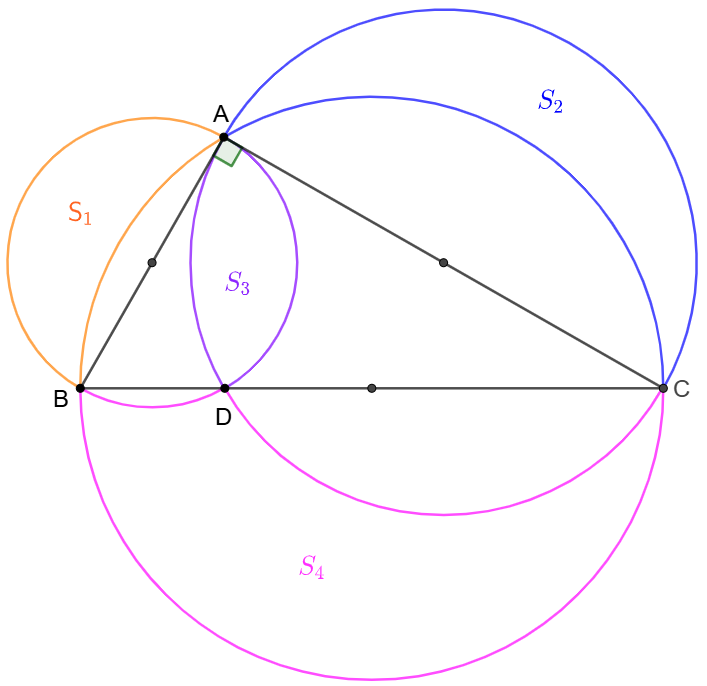
image-20250121143433974

Prove:

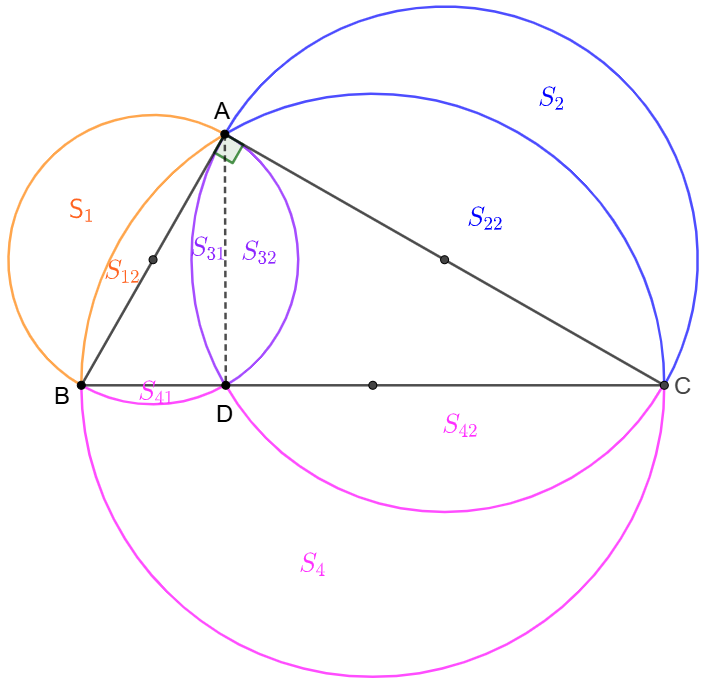image-20250121185442352 \(\begin{multline} \shoveleft \text{Two cirlces intersect at }D \text{ on }BC \implies AD\perp BC\\ \shoveleft \text{Let }AB=2a, BC=2b \implies BC=2\sqrt{a^2+b^2}\\ \shoveleft BD=\dfrac{2a^2}{\sqrt{a^2+b^2}}, CD=\dfrac{2b^2}{\sqrt{a^2+b^2}}, AD=\dfrac{2ab}{\sqrt{a^2+b^2}}\\ \shoveleft AB, AC \text{ as diameter bisects its own circle } \implies\\ \shoveleft S_1+S_{12}=S_{41}+S_{32}+[ABD]=S_{41}+S_{32}+\dfrac{2a^3b}{a^2+b^2}\\ \shoveleft S_2+S_{22}=S_{31}+S_{42}+[ACD]=S_{31}+S_{42}+\dfrac{2ab^3}{a^2+b^2}\\ \shoveleft \implies S_1+S_2+S_{12}+S_{22}=S_{31}+S_{32}+S_{41}+S_{42}+2ab\\ \shoveleft \implies S_1+S_2+S_{12}+S_{22}=S_3+S_{41}+S_{42}+[ABC]\\ \shoveleft \text{And }AB^2+AC^2=BC^2 \implies S_1+S_{12}+S_2+S_{22}=S_4+S_{41}+S_{42}\\ \shoveleft \implies S_4+S_{41}+S_{42} = S_3+S_{41}+S_{42}+[ABC]\\ \shoveleft \implies S_4-S_3=[ABC]\\ \shoveleft BC \text{ also bisects its own circle }\implies S_4+S_{41}+S_{42}=S_{12}+S_{22}+[ABC]\\ \shoveleft \implies S_3=S_{12}+S_{22}-S_{41}-S_{42} \implies S_1+S_2=[ABC]\blacksquare \end{multline}\)

01/22/2025

$AB=AC, DA=DB, DE \parallel BC$, $F$ is on $CE$ and $\angle{EAF}=\angle{ACE}$, prove that $BDEF$ is cyclic.

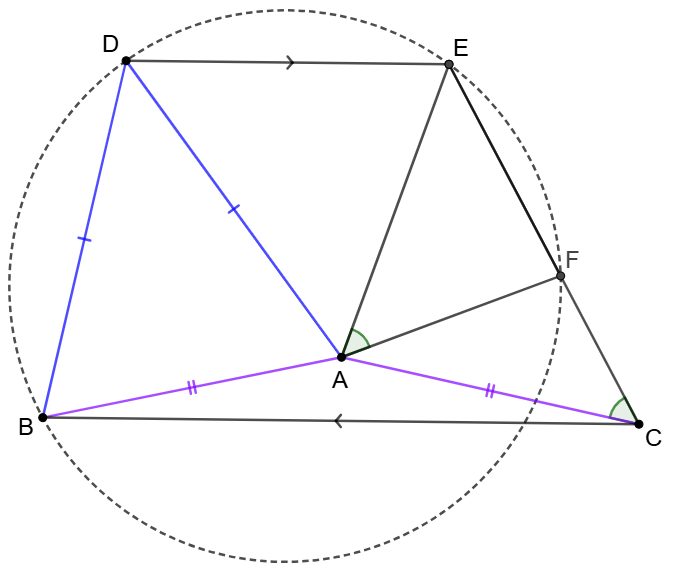
image-20250121195427672

Prove:

01/27/2025

$\angle{ABC}=100^{\circ}$ in $\triangle{ABD}$, $C$ is a point on $BD$ such that $AB=BC, AC=BD$. Find $\angle{CAD}$.

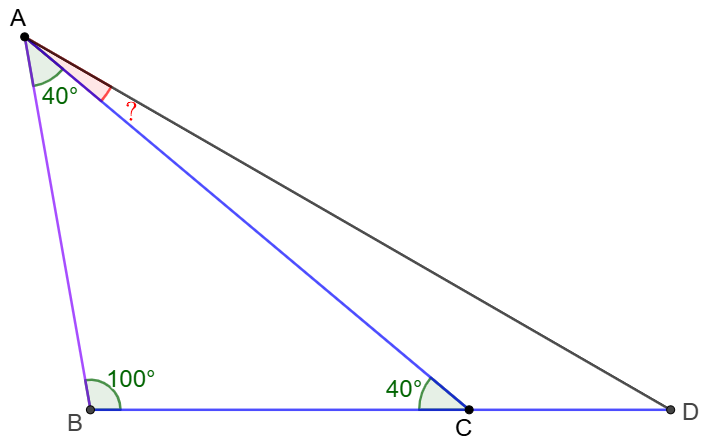
image-20250127095323482

Solve:

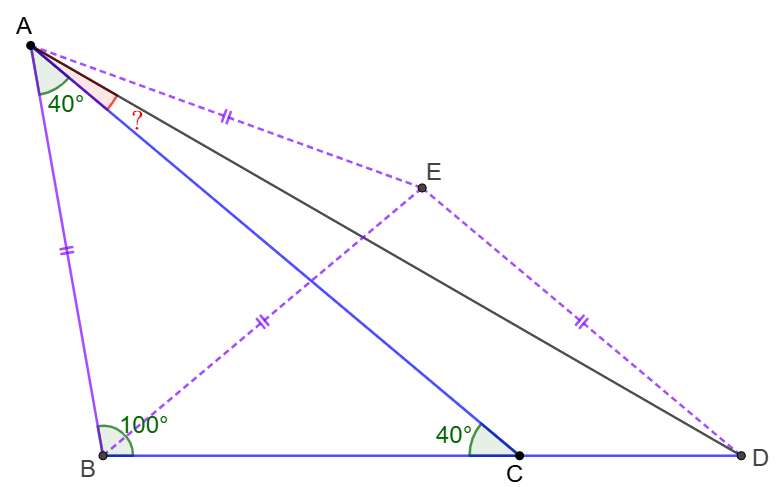image-20250127095644858 \(\begin{multline} \shoveleft \text{Make equilateral triangle} \triangle{ABE} \text{ on the same side of }AB \text{ as }C,D\\ \shoveleft \implies AB=AE=BE, \angle{ABE}=\angle{BAE}=\angle{AEB}=60^{\circ}\\ \shoveleft \implies \angle{EBD}=40^{\circ}=\angle{BAC}, AC=BD \implies \triangle{BAC}\cong\triangle{EBD}\\ \shoveleft \implies BE=DE=AE=AB, \angle{BED}=\angle{ABC}=100^{\circ}\\ \shoveleft \implies \angle{AED}=160^{\circ}\implies \angle{EAD}=10^{\circ}=\angle{EDA}\\ \shoveleft \implies \angle{CAD}=\angle{BAE}-\angle{BAC}-\angle{EAD}=60^{\circ}-40^{\circ}-10^{\circ}=\bbox[5px, border: 1px solid black]{10^{\circ}} \end{multline}\)

01/28/2025

$\angle{BAC}=2\angle{ABC}$ in $\triangle{ABC}$ and $AL$ is the bisector of $\angle{BAC}, L \in BC$. $D$ is the reflection of $L$ and $\triangle{AKD}, \triangle{EAB}$ are isosceles right triangles with hypotenuse $AD, BE$ respectively. Show that $CKE$ are collinear.

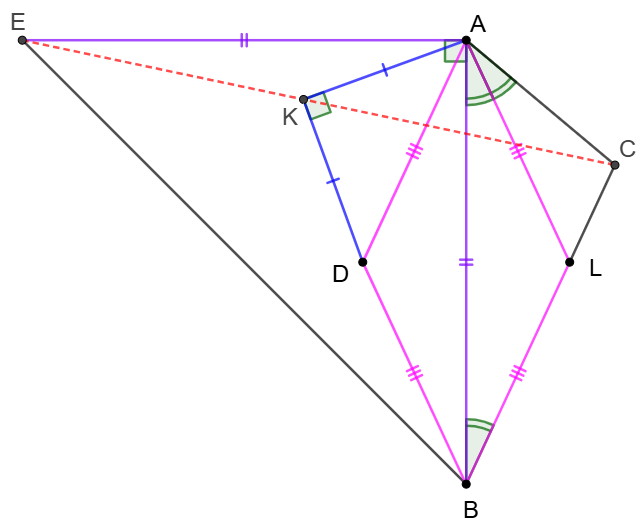
image-20250127122215678

Prove:

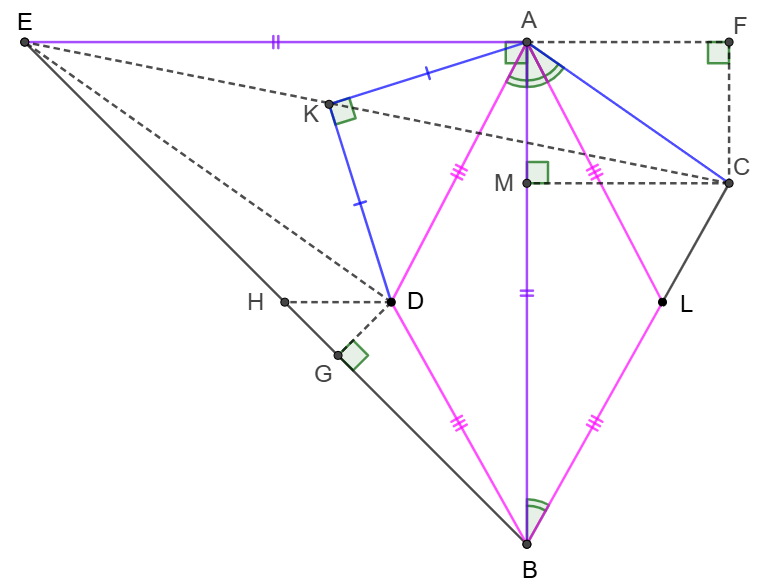image-20250203152348530 \(\begin{multline} \shoveleft \angle{BAL}=\angle{LAB}=\angle{CAL}=\angle{ABD}=\angle{DAB}\\ \shoveleft AD=AL=BD=BL, AK\perp KD, AK=KD\\ \shoveleft EA \perp AB, EA=AB \implies BD=\sqrt{2}AK, BE=\sqrt{AE}\\ \shoveleft \angle{EAK}=90^{\circ}-\angle{KAD}-\angle{DAB}=45^{\circ}-\angle{DAB}\\ \shoveleft =45^{\circ}-\angle{ABD}=\angle{EBD}\implies \triangle{AEK}\sim \triangle{BED}\\ \shoveleft \implies \angle{AEK}=\angle{BED}\\ \shoveleft \text{Make }DG \perp BE, DH \parallel EA, H=DH \cap BE\\ \shoveleft \text{Make }CM \perp AB, M=CM \cap AB, CF \perp EA, F=CF\cap EA\\ \shoveleft \text{Let }EA=AB=2a, DL=2b , \text{WLOG, suppose } a > b\\ \shoveleft \implies EH=\sqrt{2}a, DH=a-b \implies GH=DG=\dfrac{a-b}{\sqrt{2}} \\ \shoveleft \implies tan\angle{BED}=\dfrac{\dfrac{a-b}{\sqrt{2}}}{\sqrt{2}a+ \dfrac{a-b}{\sqrt{2}}}=\dfrac{a-b}{3a-b}\\ \shoveleft BM=2a-AM, tan \angle{ABC}=\dfrac{CM}{BM}=\dfrac{b}{a} \implies CM=\dfrac{b}{a}(2a-AM)\\ \shoveleft tan\angle{CAM}=tan(2\angle{ABC})=\dfrac{2\cdot tan \angle{ABC}}{1-tan^2{\angle{ABC}}}=\dfrac{2ab}{a^2-b^2}\\ \shoveleft \implies \dfrac{CM}{AM}=\dfrac{2ab}{a^2-b^2} \implies AM=\dfrac{2a(a^2-b^2)}{3a^2-b^2}, CM=\dfrac{4a^2b}{3a^2-b^2}\\ \shoveleft \implies tan\angle{CEA}=\dfrac{AM}{AE+CM}=\dfrac{\dfrac{2a(a^2-b^2)}{3a^2-b^2}}{2a+\dfrac{4a^2b}{3a^2-b^2}}=\dfrac{a-b}{3a-b}=tan \angle{BED}\\ \shoveleft \implies \angle{BED}=\angle{CEA}=\angle{AEK} \implies CKE \text{ are collinear} \blacksquare \end{multline}\)

01/30/2025

Three chords are of length $a,a,b$ in a semi-circle as shown in figure. Find the diameter $x$.

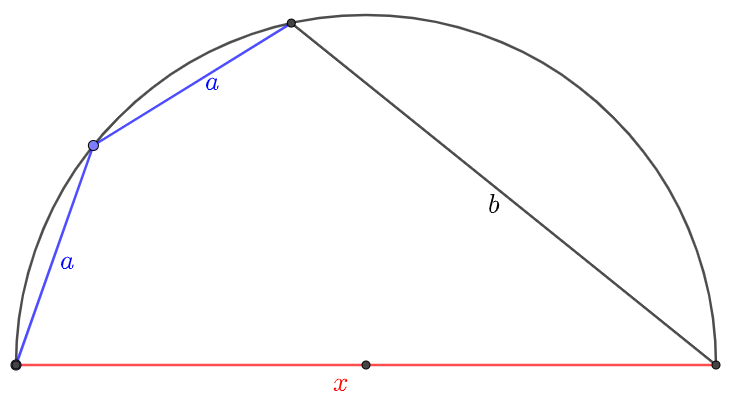
image-20250201200323921

Solve:

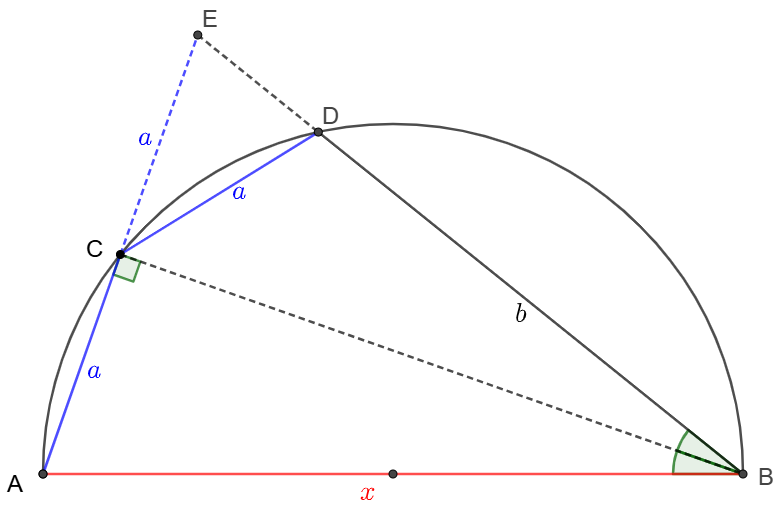image-20250201200639306 \(\begin{multline} \shoveleft \text{Extend }AC, BD \text{ so }E=AC \cap BD\\ \shoveleft AC=CD \implies \angle{ABC}=\angle{CBD}\\ \shoveleft BC \perp AC \implies \triangle{ABC}\cong\triangle{EBC}\\ \shoveleft \implies CE=AC=a, BE=AB=x\\ \shoveleft \implies EC \cdot EA = EB \cdot ED\implies\\ \shoveleft 2a^2=x(x-b)\implies x=\bbox[5px, border: 1px solid black]{\dfrac{b+\sqrt{b^2+8a^2}}{2}} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search