11/02/2024
$P$ is a point on the inscribed circle of equilateral triangle $\triangle{ABC}$ such that $BP=\sqrt{37}, CP=\sqrt{21}$. Find $AP$.
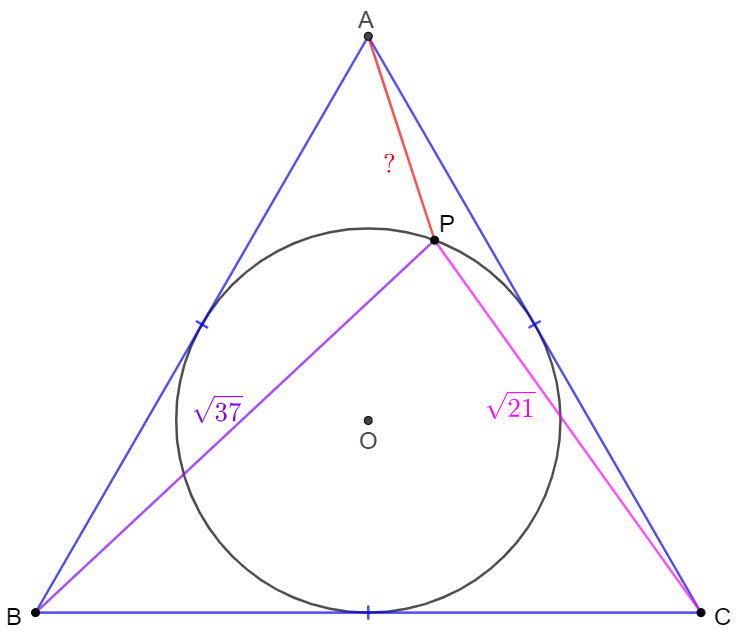
Solve:
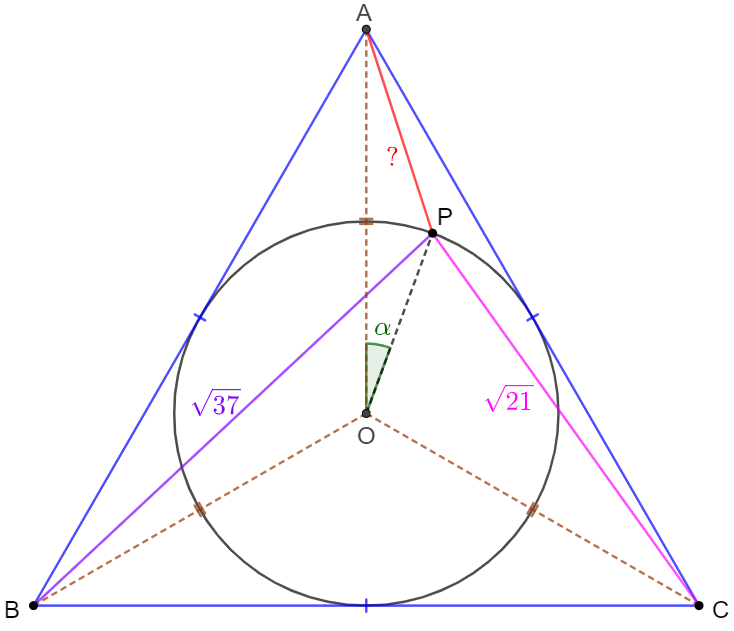 \(\begin{multline}
\shoveleft \text{Let }\angle{AOP}=\alpha, PO=r \implies AB=BC=CA=d=2\sqrt{3}r \\
\shoveleft \implies cos\alpha=\dfrac{4r^2+r^2-AP^2}{4r^2}\\
\shoveleft cos(120^{\circ}+\alpha)=\dfrac{4r^2+r^2-BP^2}{4r^2}\\
\shoveleft cos(120^{\circ}-\alpha)=\dfrac{4r^2+r^2-CP^2}{4r^2}\\
\shoveleft \text{Since }cos\alpha+cos(120^{\circ}-\alpha)+cos(120^{\circ}+\alpha)=0\\
\shoveleft \implies AP^2+BP^2+CP^2=15r^2=\dfrac{5}{4}d^2\\
\shoveleft \implies \dfrac{4}{5}(AP^2+BP^2+CP^2)=d^2\\
\shoveleft \text{From reference we know that}\\
\shoveleft 3(AP^4+BP^4+CP^4+d^4)=(AP^2+BP^2+CP^2+d^2)^2\\
\shoveleft \implies 3(AP^4+BP^4+CP^4)+3d^4=(\dfrac{9}{4}d^2)^2=\dfrac{81}{16}d^4\\
\shoveleft \implies AP^4+BP^4+CP^4=\dfrac{11}{16}d^4\\
\shoveleft \implies \dfrac{16}{11}(AP^4+BP^4+CP^4)=d^4=\dfrac{16}{25}(AP^2+BP^2+CP^2)^2\\
\shoveleft \implies \dfrac{AP^4+BP^4+CP^4}{(AP^2+BP^2+CP^2)^2}=\dfrac{11}{25}\implies AP=\bbox[5px, border: 1px solid black]{\sqrt{7}} \text{ or }\bbox[5px, border: 1px solid black]{\sqrt{\dfrac{589}{7}}}\\
\shoveleft
\end{multline}\)
Note: The referred equation is proved here. By using Cayley-Menger determinant the volume of Tetrahedron $PABC$ is given as $288V^2=d^2((a^2+b^2+c^2+d^2)^2-3(a^4+b^4+c^4+d^4))$. Since the tetrahedron is flat, its volume is zero.
\(\begin{multline}
\shoveleft \text{Let }\angle{AOP}=\alpha, PO=r \implies AB=BC=CA=d=2\sqrt{3}r \\
\shoveleft \implies cos\alpha=\dfrac{4r^2+r^2-AP^2}{4r^2}\\
\shoveleft cos(120^{\circ}+\alpha)=\dfrac{4r^2+r^2-BP^2}{4r^2}\\
\shoveleft cos(120^{\circ}-\alpha)=\dfrac{4r^2+r^2-CP^2}{4r^2}\\
\shoveleft \text{Since }cos\alpha+cos(120^{\circ}-\alpha)+cos(120^{\circ}+\alpha)=0\\
\shoveleft \implies AP^2+BP^2+CP^2=15r^2=\dfrac{5}{4}d^2\\
\shoveleft \implies \dfrac{4}{5}(AP^2+BP^2+CP^2)=d^2\\
\shoveleft \text{From reference we know that}\\
\shoveleft 3(AP^4+BP^4+CP^4+d^4)=(AP^2+BP^2+CP^2+d^2)^2\\
\shoveleft \implies 3(AP^4+BP^4+CP^4)+3d^4=(\dfrac{9}{4}d^2)^2=\dfrac{81}{16}d^4\\
\shoveleft \implies AP^4+BP^4+CP^4=\dfrac{11}{16}d^4\\
\shoveleft \implies \dfrac{16}{11}(AP^4+BP^4+CP^4)=d^4=\dfrac{16}{25}(AP^2+BP^2+CP^2)^2\\
\shoveleft \implies \dfrac{AP^4+BP^4+CP^4}{(AP^2+BP^2+CP^2)^2}=\dfrac{11}{25}\implies AP=\bbox[5px, border: 1px solid black]{\sqrt{7}} \text{ or }\bbox[5px, border: 1px solid black]{\sqrt{\dfrac{589}{7}}}\\
\shoveleft
\end{multline}\)
Note: The referred equation is proved here. By using Cayley-Menger determinant the volume of Tetrahedron $PABC$ is given as $288V^2=d^2((a^2+b^2+c^2+d^2)^2-3(a^4+b^4+c^4+d^4))$. Since the tetrahedron is flat, its volume is zero.
11/11/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=20^{\circ}$, $\angle{DAC}=80^{\circ}$, $\angle{ABD}=10^{\circ}$, $\angle{CBD}=20^{\circ}$. Find $\angle{ACD}$.
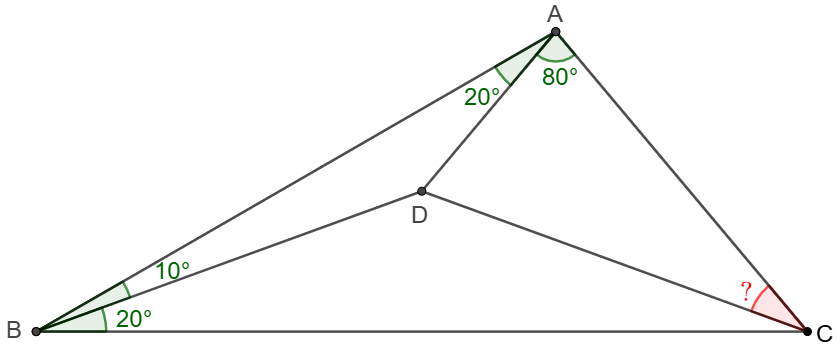
Solve:
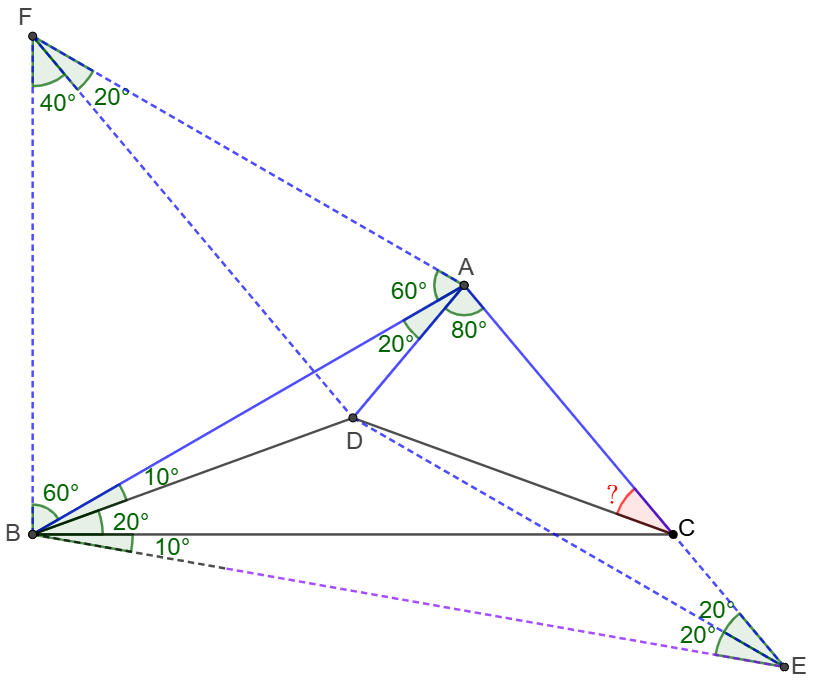 \(\begin{multline}
\shoveleft \text{Extend }AC \text{ to } E \text{ such that }AE=AB \implies \angle{ABE}=\angle{AEB}=40^{\circ} \\
\shoveleft \text{Make }\triangle{F} \text{ to be the circumcenter of }\triangle{ABD}\implies \\
\shoveleft FA=FB=FD, \angle{AFD}=2\angle{ABD}=20^{\circ}, \angle{BFD}=2\angle{BAD}=40^{\circ}\\
\shoveleft \implies \triangle{ABF}\text{ is equilateral} \implies \\
\shoveleft FA=AB=AE, \angle{FAB}=60^{\circ}\implies \angle{FAD}=80^{\circ}=\angle{DAE}\\
\shoveleft \implies \triangle{FAD}\cong\triangle{EAD}\implies \angle{AED}=\angle{AFD}=20^{\circ}=\angle{CBD}\\
\shoveleft \implies BDCE \text{ is cyclic} \implies \angle{DEB}=40^{\circ}-20^{\circ}=20^{\circ}=\angle{BCD}\\
\shoveleft \implies \angle{ACD}=50^{\circ}-20^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Extend }AC \text{ to } E \text{ such that }AE=AB \implies \angle{ABE}=\angle{AEB}=40^{\circ} \\
\shoveleft \text{Make }\triangle{F} \text{ to be the circumcenter of }\triangle{ABD}\implies \\
\shoveleft FA=FB=FD, \angle{AFD}=2\angle{ABD}=20^{\circ}, \angle{BFD}=2\angle{BAD}=40^{\circ}\\
\shoveleft \implies \triangle{ABF}\text{ is equilateral} \implies \\
\shoveleft FA=AB=AE, \angle{FAB}=60^{\circ}\implies \angle{FAD}=80^{\circ}=\angle{DAE}\\
\shoveleft \implies \triangle{FAD}\cong\triangle{EAD}\implies \angle{AED}=\angle{AFD}=20^{\circ}=\angle{CBD}\\
\shoveleft \implies BDCE \text{ is cyclic} \implies \angle{DEB}=40^{\circ}-20^{\circ}=20^{\circ}=\angle{BCD}\\
\shoveleft \implies \angle{ACD}=50^{\circ}-20^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
11/12/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=30^{\circ}$, $\angle{CAD}=50^{\circ}$, $\angle{ABD}=10^{\circ}$, $\angle{CBD}=20^{\circ}$. Find $\angle{ACD}$.
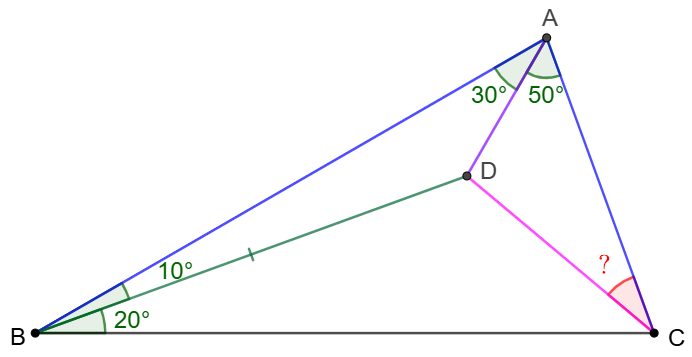
Solve:
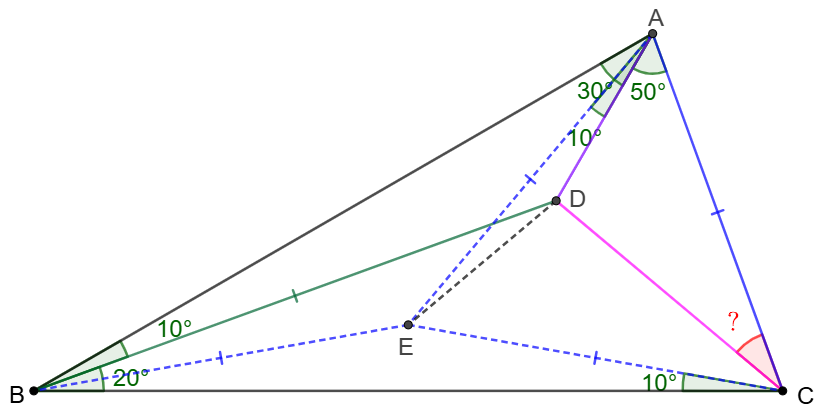 \(\begin{multline}
\shoveleft \text{Make }\triangle{ACE} \text{ to be equilateral } \implies \\
\shoveleft \angle{EAD}=10^{\circ}, AE=EC, \angle{AEC}=60^{\circ}=2\angle{ABC}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies BE=AE=CE \implies \angle{EBC}=\angle{ECB}=10^{\circ}\\
\shoveleft \implies \angle{EBD}=\angle{EAD}\implies ADEB \text{ is cyclic}\\
\shoveleft \implies \angle{AED}=\angle{ABD}=10^{\circ}=\angle{EAD}\implies AD=ED\\
\shoveleft \implies \triangle{ACD}\cong\triangle{ECD}\implies \angle{ACD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }\triangle{ACE} \text{ to be equilateral } \implies \\
\shoveleft \angle{EAD}=10^{\circ}, AE=EC, \angle{AEC}=60^{\circ}=2\angle{ABC}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies BE=AE=CE \implies \angle{EBC}=\angle{ECB}=10^{\circ}\\
\shoveleft \implies \angle{EBD}=\angle{EAD}\implies ADEB \text{ is cyclic}\\
\shoveleft \implies \angle{AED}=\angle{ABD}=10^{\circ}=\angle{EAD}\implies AD=ED\\
\shoveleft \implies \triangle{ACD}\cong\triangle{ECD}\implies \angle{ACD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\
\end{multline}\)
11/13/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=20^{\circ}$, $\angle{CAD}=100^{\circ}$, $\angle{ABD}=10^{\circ}$, $\angle{CBD}=10^{\circ}$. Find $\angle{BCD}$.
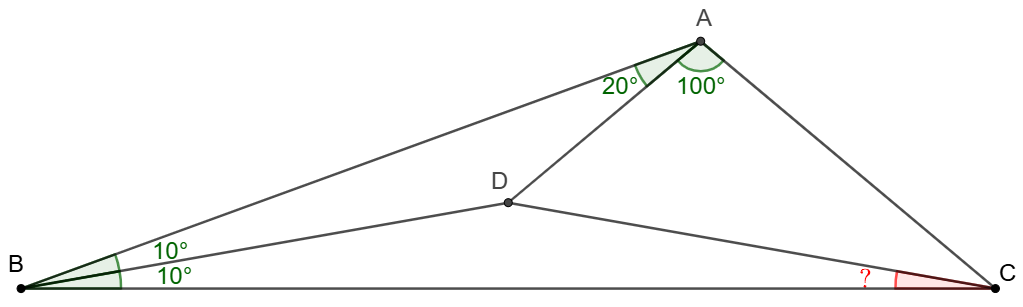
Solve:
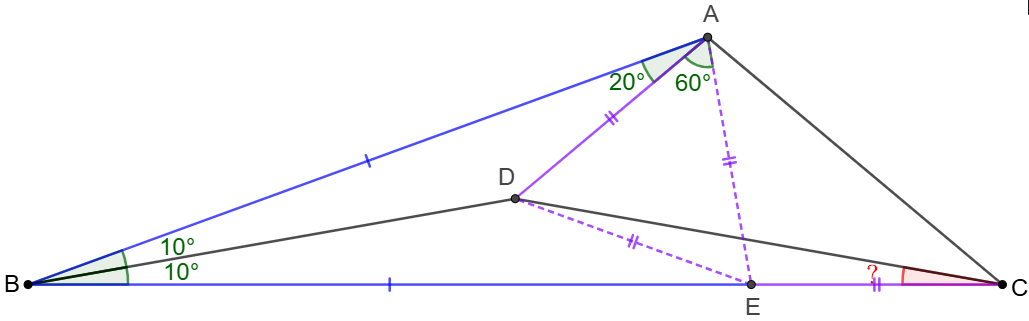 \(\begin{multline}
\shoveleft \text{Let }E \text{ on }BC \text{ such that }AB=EB \implies \\
\shoveleft \angle{BAE}=\angle{BEA}=80^{\circ}, \triangle{ABD}\cong\triangle{EBD}\\
\shoveleft \implies AD=DE, \angle{DAE}=60^{\circ}\implies\\
\shoveleft \triangle{ADE}\text{ is equilateral }\implies\\
\shoveleft DE=AE, \angle{EAC}=40^{\circ}=\angle{ACE} \implies CE=AE \\
\shoveleft \implies E\text{ is the circumcenter of }\triangle{ACD}\\
\shoveleft \implies \angle{ACD}=\dfrac{\angle{AED}}{2}=30^{\circ}\implies \angle{BCD}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ on }BC \text{ such that }AB=EB \implies \\
\shoveleft \angle{BAE}=\angle{BEA}=80^{\circ}, \triangle{ABD}\cong\triangle{EBD}\\
\shoveleft \implies AD=DE, \angle{DAE}=60^{\circ}\implies\\
\shoveleft \triangle{ADE}\text{ is equilateral }\implies\\
\shoveleft DE=AE, \angle{EAC}=40^{\circ}=\angle{ACE} \implies CE=AE \\
\shoveleft \implies E\text{ is the circumcenter of }\triangle{ACD}\\
\shoveleft \implies \angle{ACD}=\dfrac{\angle{AED}}{2}=30^{\circ}\implies \angle{BCD}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
11/14/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=\angle{CBD}=20^{\circ}$, $\angle{BCD}=20^{\circ}$, $AB=BD$, Find $\angle{ACD}$.
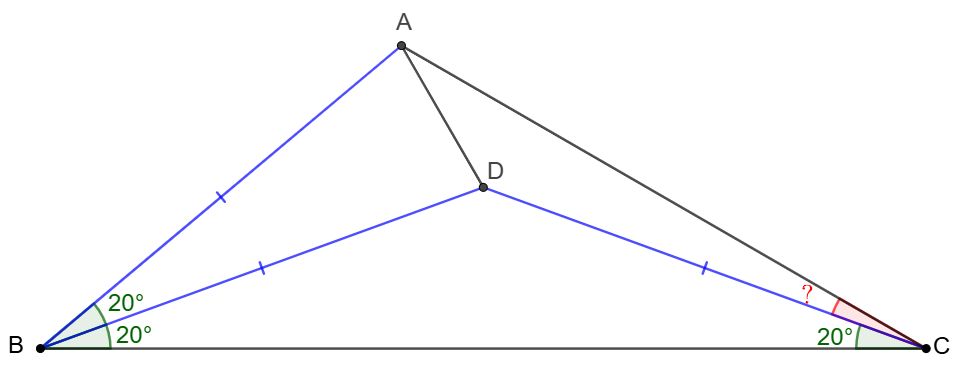
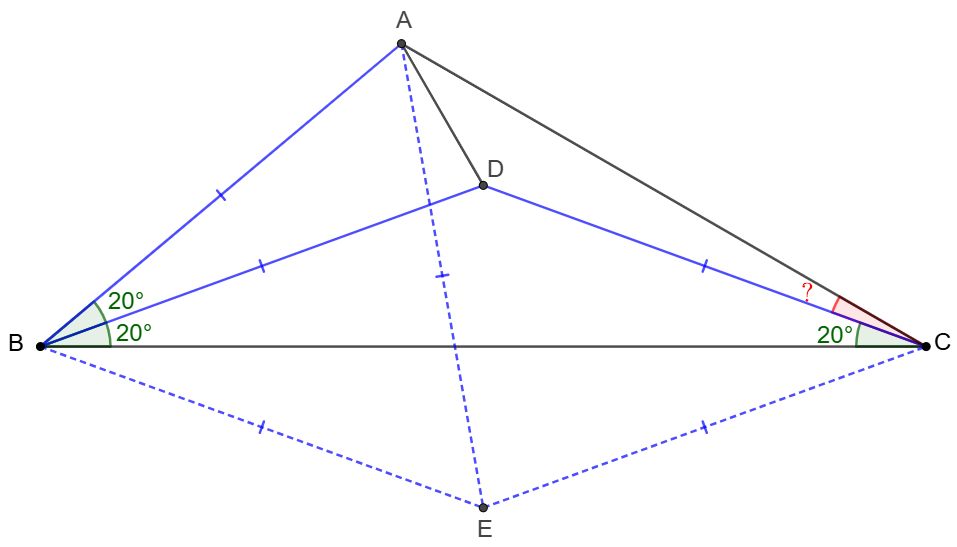
Solve:
 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the reflection of }D \text{ along }BC \\
\shoveleft \implies BD=BE=AB=CD=CE, \angle{EBC}=\angle{CBD}=20^{\circ}\\
\shoveleft \implies \angle{ABE}=60^{\circ}\implies \triangle{ABE}\text{ is equilateral}\\
\shoveleft \implies AE=BE=CE \implies E\text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies \angle{ACB}=\dfrac{\angle{AEB}}{2}=30^{\circ}\implies \angle{ACD}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the reflection of }D \text{ along }BC \\
\shoveleft \implies BD=BE=AB=CD=CE, \angle{EBC}=\angle{CBD}=20^{\circ}\\
\shoveleft \implies \angle{ABE}=60^{\circ}\implies \triangle{ABE}\text{ is equilateral}\\
\shoveleft \implies AE=BE=CE \implies E\text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies \angle{ACB}=\dfrac{\angle{AEB}}{2}=30^{\circ}\implies \angle{ACD}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
11/15/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=30^{\circ}$, $\angle{CBD}=10^{\circ}$, $\angle{BCD}=20^{\circ}$, $\angle{ACD}=10^{\circ}$. Find $\angle{BAD}$.
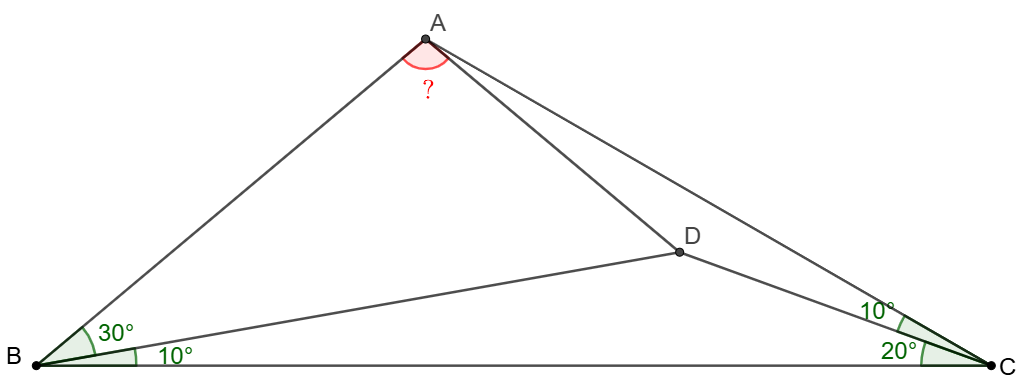
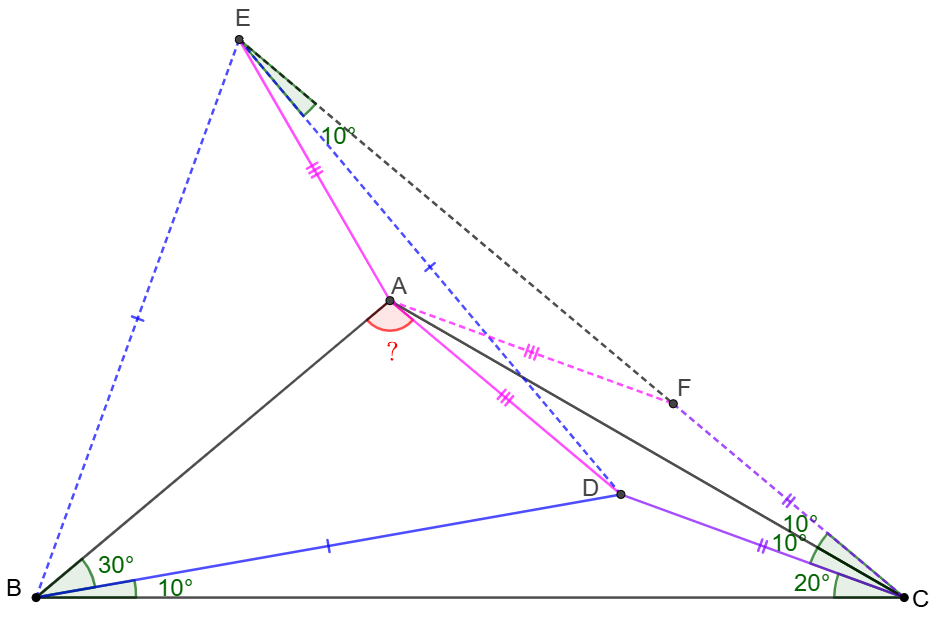
Solve:
 \(\begin{multline}
\shoveleft \text{Make equilateral triangle }\triangle{BDE} \text{ on the same side of }BC \text{ as }A\\
\shoveleft \implies BD=DE, \angle{CDE}=150^{\circ}=\angle{BDC}, \triangle{ABD}\cong\triangle{AEB}\implies \\
\shoveleft AD=AE, \triangle{CDE}\cong\triangle{CDB}\implies\\
\shoveleft \angle{DCE}=\angle{DCB}=20^{\circ}, \angle{CBD}=\angle{CED}=10^{\circ} \implies \angle{ACF}=10^{\circ}\\
\shoveleft \text{Make }F \text{ on }CE \text{ such that }CD=CF\implies \triangle{ACF}\cong\triangle{ACD}\implies \\
\shoveleft \angle{ADC}=\angle{AFC}, AD=AF=AE \implies \angle{AEF}=\angle{AFE}\implies\\
\shoveleft \angle{AFE}+\angle{AFC}=\angle{AEF}+\angle{ADC}=180^{\circ}\implies EADC\text{ is cyclic}\\
\shoveleft \implies \angle{CAD}=\angle{CED}=10^{\circ}\implies \angle{BAD}=\bbox[5px, border: 1px solid black]{100^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make equilateral triangle }\triangle{BDE} \text{ on the same side of }BC \text{ as }A\\
\shoveleft \implies BD=DE, \angle{CDE}=150^{\circ}=\angle{BDC}, \triangle{ABD}\cong\triangle{AEB}\implies \\
\shoveleft AD=AE, \triangle{CDE}\cong\triangle{CDB}\implies\\
\shoveleft \angle{DCE}=\angle{DCB}=20^{\circ}, \angle{CBD}=\angle{CED}=10^{\circ} \implies \angle{ACF}=10^{\circ}\\
\shoveleft \text{Make }F \text{ on }CE \text{ such that }CD=CF\implies \triangle{ACF}\cong\triangle{ACD}\implies \\
\shoveleft \angle{ADC}=\angle{AFC}, AD=AF=AE \implies \angle{AEF}=\angle{AFE}\implies\\
\shoveleft \angle{AFE}+\angle{AFC}=\angle{AEF}+\angle{ADC}=180^{\circ}\implies EADC\text{ is cyclic}\\
\shoveleft \implies \angle{CAD}=\angle{CED}=10^{\circ}\implies \angle{BAD}=\bbox[5px, border: 1px solid black]{100^{\circ}}
\end{multline}\)
11/16/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=73^{\circ}$, $\angle{CAD}=30^{\circ}$, $\angle{ACD}=\angle{BCD}=13^{\circ}$. Find $\angle{BPC}$.
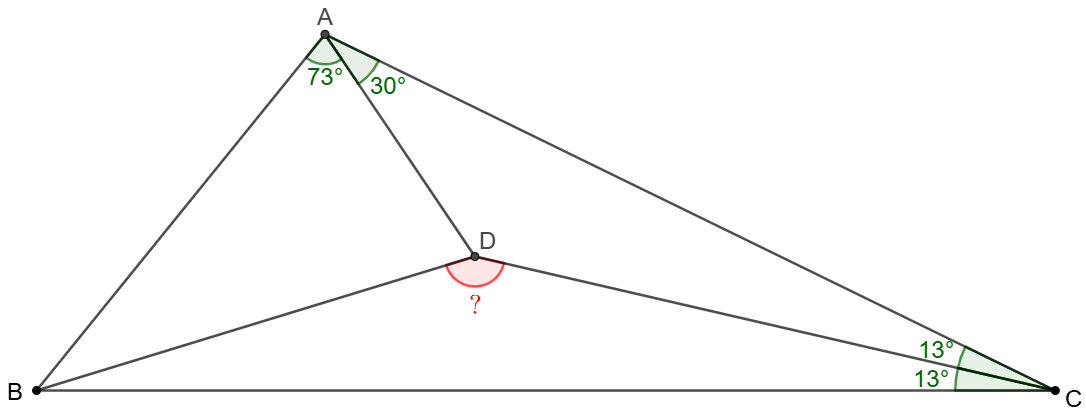
Solve:
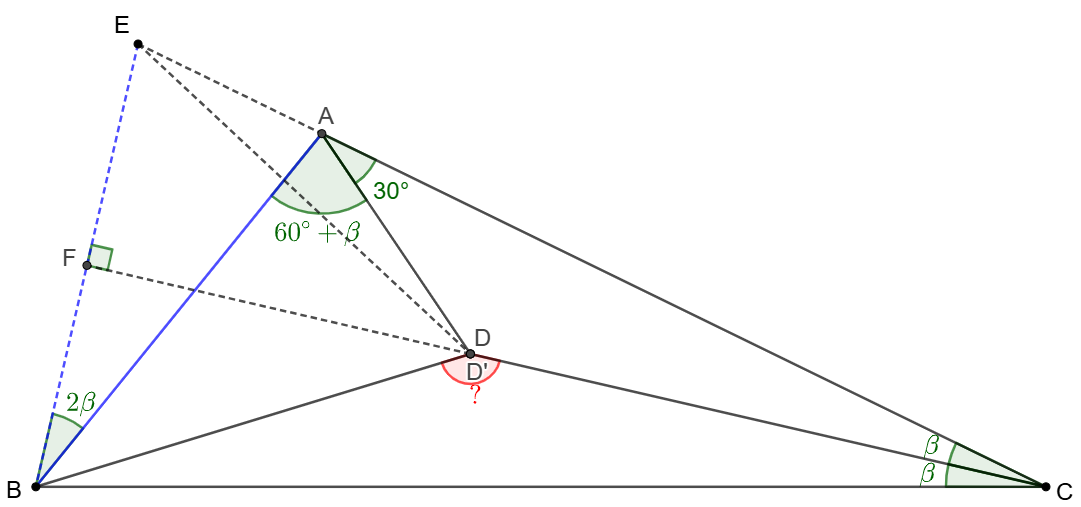 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the reflection of }B \text{ along }CD\\
\shoveleft \implies \angle{EAB}=77^{\circ}=\angle{BEC}=\angle{EBC}\\
\shoveleft \text{Consider a more general construction: }\\
\shoveleft \angle{ACD}=\angle{BCD}=\beta, \angle{BAD}=60^{\circ}+\beta\\
\shoveleft \angle{CAD}=30^{\circ}, E \text{ is reflection of }B \text{ along }CD\\
\shoveleft \text{Extend }CD \text{ and intersects with }BE \text{ at }F\\
\shoveleft \implies \angle{BEC}=90^{\circ}-\beta=\angle{EBC}=\angle{EAB}\\
\shoveleft \implies \triangle{BCE}\sim\triangle{BEA}\implies BE^2=EA\cdot EC\\
\shoveleft \text{Let }D' \text{ on }CF \text{ such that }\triangle{D'BE}\text{ is equilateral}\\
\shoveleft \implies BE=EG' \implies EG'^2=EA \cdot EC \\
\shoveleft \implies \triangle{EAD'}\sim\triangle{EG'C}\\
\shoveleft \implies \angle{AD'C}=\angle{AED'}+\angle{AD'E}\\
\shoveleft =\angle{EAD'}+\angle{ECD'}=\angle{ED'F}=30^{\circ}=\angle{DAC}\\
\shoveleft D', D \text{ is identical}\implies \angle{EDF}=\angle{BDF}=30^{\circ}\\
\shoveleft \implies \angle{BDC}=\bbox[5px, border: 1px solid black]{150^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the reflection of }B \text{ along }CD\\
\shoveleft \implies \angle{EAB}=77^{\circ}=\angle{BEC}=\angle{EBC}\\
\shoveleft \text{Consider a more general construction: }\\
\shoveleft \angle{ACD}=\angle{BCD}=\beta, \angle{BAD}=60^{\circ}+\beta\\
\shoveleft \angle{CAD}=30^{\circ}, E \text{ is reflection of }B \text{ along }CD\\
\shoveleft \text{Extend }CD \text{ and intersects with }BE \text{ at }F\\
\shoveleft \implies \angle{BEC}=90^{\circ}-\beta=\angle{EBC}=\angle{EAB}\\
\shoveleft \implies \triangle{BCE}\sim\triangle{BEA}\implies BE^2=EA\cdot EC\\
\shoveleft \text{Let }D' \text{ on }CF \text{ such that }\triangle{D'BE}\text{ is equilateral}\\
\shoveleft \implies BE=EG' \implies EG'^2=EA \cdot EC \\
\shoveleft \implies \triangle{EAD'}\sim\triangle{EG'C}\\
\shoveleft \implies \angle{AD'C}=\angle{AED'}+\angle{AD'E}\\
\shoveleft =\angle{EAD'}+\angle{ECD'}=\angle{ED'F}=30^{\circ}=\angle{DAC}\\
\shoveleft D', D \text{ is identical}\implies \angle{EDF}=\angle{BDF}=30^{\circ}\\
\shoveleft \implies \angle{BDC}=\bbox[5px, border: 1px solid black]{150^{\circ}}
\end{multline}\)
11/17/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=30^{\circ}$, $\angle{ABD}=48^{\circ}$, $\angle{BCD}=\angle{CBD}=36^{\circ}$. Find $\angle{ACD}$.
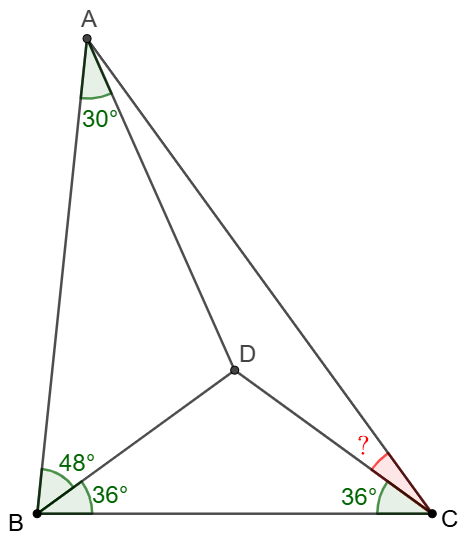
Solve:
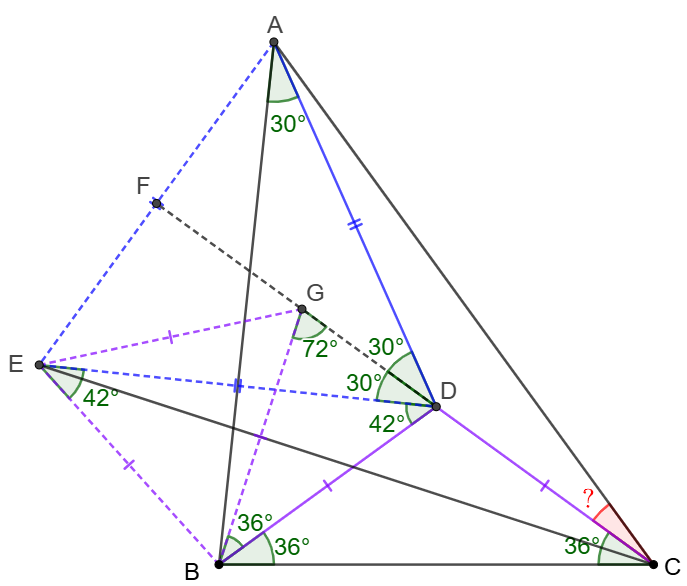 \(\begin{multline}
\shoveleft \text{Make }\triangle{ADE} \text{ to be equilateral} \implies \\
\shoveleft AE=AD=ED, \angle{EAB}=\angle{DAB}=30^{\circ}\\
\shoveleft \implies \triangle{ABE}\cong \triangle{ABD}\implies\\
\shoveleft BD=BE, \angle{EBA}=\angle{DBA}=48^{\circ}\implies \\
\shoveleft \angle{BDE}=\angle{BED}=42^{\circ}\\
\shoveleft \text{Extend }CD \text{ to }F \in AE, \text{ let }G \text{ on }CF \text{ such that } \\
\shoveleft BD=BG=BE \implies \angle{BGD}=\angle{BDG}=72^{\circ}\\
\shoveleft\implies \angle{DBG}=36^{\circ}, \angle{EDG}=30^{\circ}=\angle{ADG}\\
\shoveleft \implies \angle{CDA}=\angle{CDE}, \angle{CBG}=\angle{CGB}, \angle{EBG}=96^{\circ}-36^{\circ}=60^{\circ}\\
\shoveleft \implies BC=GC, \triangle{BEG}\text{ is equilateral} \implies EB=EG \\
\shoveleft \implies \triangle{EBC}\cong\triangle{EGC}\implies \angle{DCE}=\angle{BCE}=18^{\circ}\\
\shoveleft \text{And }\triangle{CAD}\cong\triangle{CED}\implies \angle{ACD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }\triangle{ADE} \text{ to be equilateral} \implies \\
\shoveleft AE=AD=ED, \angle{EAB}=\angle{DAB}=30^{\circ}\\
\shoveleft \implies \triangle{ABE}\cong \triangle{ABD}\implies\\
\shoveleft BD=BE, \angle{EBA}=\angle{DBA}=48^{\circ}\implies \\
\shoveleft \angle{BDE}=\angle{BED}=42^{\circ}\\
\shoveleft \text{Extend }CD \text{ to }F \in AE, \text{ let }G \text{ on }CF \text{ such that } \\
\shoveleft BD=BG=BE \implies \angle{BGD}=\angle{BDG}=72^{\circ}\\
\shoveleft\implies \angle{DBG}=36^{\circ}, \angle{EDG}=30^{\circ}=\angle{ADG}\\
\shoveleft \implies \angle{CDA}=\angle{CDE}, \angle{CBG}=\angle{CGB}, \angle{EBG}=96^{\circ}-36^{\circ}=60^{\circ}\\
\shoveleft \implies BC=GC, \triangle{BEG}\text{ is equilateral} \implies EB=EG \\
\shoveleft \implies \triangle{EBC}\cong\triangle{EGC}\implies \angle{DCE}=\angle{BCE}=18^{\circ}\\
\shoveleft \text{And }\triangle{CAD}\cong\triangle{CED}\implies \angle{ACD}=\angle{ECD}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
11/18/2024
$P$ is any point on $A$-symmedian and $DE \parallel BC$. $DP\cap BE=K, EP \cap CD=L$, prove that $\angle{BAK}=\angle{CAL}$
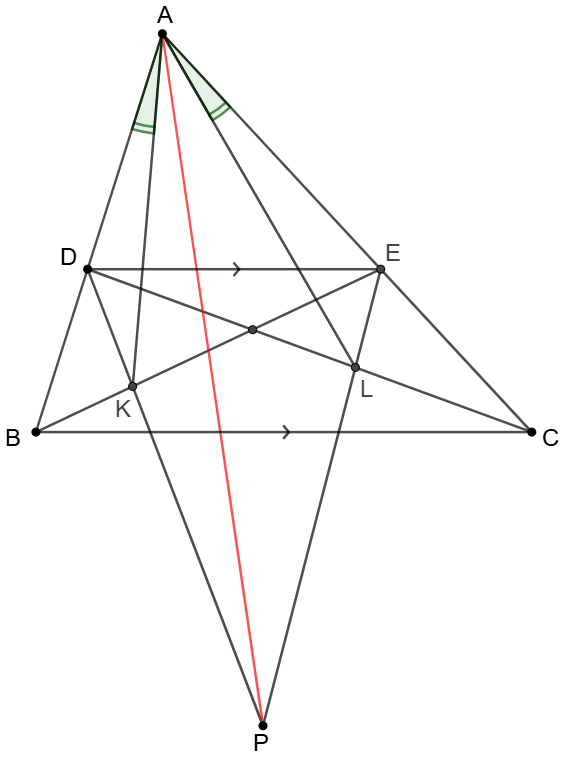
Prove:
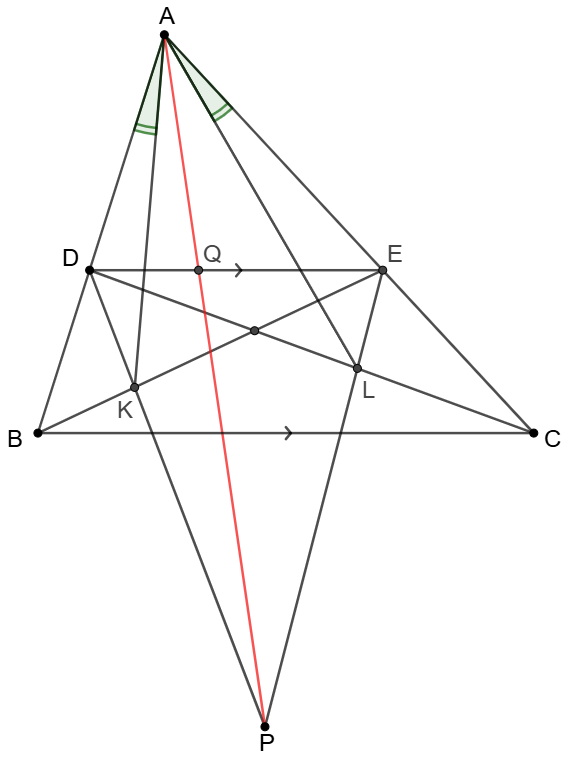 \(\begin{multline}
\shoveleft \text{Applying Ceva's Theorem in trigonometric form to }\triangle{ADE} \text{ and points }K,L:\\
\shoveleft \dfrac{sin\angle{KAD}}{sin\angle{KAE}}\dfrac{sin\angle{AEK}}{sin\angle{KED}}\dfrac{sin\angle{KDE}}{sin\angle{KDA}}=1\\
\shoveleft \dfrac{sin\angle{EAL}}{sin\angle{LAD}}\dfrac{sin\angle{LDA}}{sin\angle{LDE}}\dfrac{sin\angle{LED}}{sin\angle{LEA}}=1\\
\shoveleft \text{Let }Q=AP\cap DE, \text{from Law of sines we know}\\
\shoveleft \dfrac{sin\angle{AEK}}{sin\angle{KED}}=\dfrac{AB}{DB}\dfrac{DE}{AE}, \dfrac{sin\angle{KDE}}{sin\angle{KDA}}=\dfrac{PQ}{PA}\dfrac{AD}{QD}\\
\shoveleft \dfrac{sin\angle{LDA}}{sin\angle{LDE}}=\dfrac{AC}{EC}\dfrac{DE}{AD}, \dfrac{sin\angle{LED}}{sin\angle{LEA}}=\dfrac{PQ}{PA}\dfrac{AE}{QE}\\
\shoveleft \implies \dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{DB \cdot AC}{AB \cdot EC}\dfrac{QD}{QE}\dfrac{AE^2}{AD^2}\dfrac{sin\angle{LAD}}{sin\angle{KAE}}\\
\shoveleft AP \text{ is A-symmedian} \implies \dfrac{QD}{QE}=\dfrac{AD^2}{AE^2}\\
\shoveleft DE\parallel BC \implies \dfrac{DB}{AB}=\dfrac{EC}{AC}\implies\dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{sin\angle{LAD}}{sin\angle{KAE}}\\
\shoveleft \implies \dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{sin(\angle{KAD}+\angle{KAL})}{sin(\angle{EAL}+\angle{KAL})}\\
\shoveleft \implies sin(\angle{KAD}-\angle{EAL})sin\angle{KAL}=0\implies \angle{KAD}=\angle{EAL}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Applying Ceva's Theorem in trigonometric form to }\triangle{ADE} \text{ and points }K,L:\\
\shoveleft \dfrac{sin\angle{KAD}}{sin\angle{KAE}}\dfrac{sin\angle{AEK}}{sin\angle{KED}}\dfrac{sin\angle{KDE}}{sin\angle{KDA}}=1\\
\shoveleft \dfrac{sin\angle{EAL}}{sin\angle{LAD}}\dfrac{sin\angle{LDA}}{sin\angle{LDE}}\dfrac{sin\angle{LED}}{sin\angle{LEA}}=1\\
\shoveleft \text{Let }Q=AP\cap DE, \text{from Law of sines we know}\\
\shoveleft \dfrac{sin\angle{AEK}}{sin\angle{KED}}=\dfrac{AB}{DB}\dfrac{DE}{AE}, \dfrac{sin\angle{KDE}}{sin\angle{KDA}}=\dfrac{PQ}{PA}\dfrac{AD}{QD}\\
\shoveleft \dfrac{sin\angle{LDA}}{sin\angle{LDE}}=\dfrac{AC}{EC}\dfrac{DE}{AD}, \dfrac{sin\angle{LED}}{sin\angle{LEA}}=\dfrac{PQ}{PA}\dfrac{AE}{QE}\\
\shoveleft \implies \dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{DB \cdot AC}{AB \cdot EC}\dfrac{QD}{QE}\dfrac{AE^2}{AD^2}\dfrac{sin\angle{LAD}}{sin\angle{KAE}}\\
\shoveleft AP \text{ is A-symmedian} \implies \dfrac{QD}{QE}=\dfrac{AD^2}{AE^2}\\
\shoveleft DE\parallel BC \implies \dfrac{DB}{AB}=\dfrac{EC}{AC}\implies\dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{sin\angle{LAD}}{sin\angle{KAE}}\\
\shoveleft \implies \dfrac{sin\angle{KAD}}{sin\angle{EAL}}=\dfrac{sin(\angle{KAD}+\angle{KAL})}{sin(\angle{EAL}+\angle{KAL})}\\
\shoveleft \implies sin(\angle{KAD}-\angle{EAL})sin\angle{KAL}=0\implies \angle{KAD}=\angle{EAL}\blacksquare
\end{multline}\)
11/19/2024
$\triangle{ABC}$ is an isosceles with $\angle{ABC}=\angle{ACB}=40^{\circ}$. Extend $AC$ to $D$ such that $BC=AD$. Find $\angle{ADB}$.
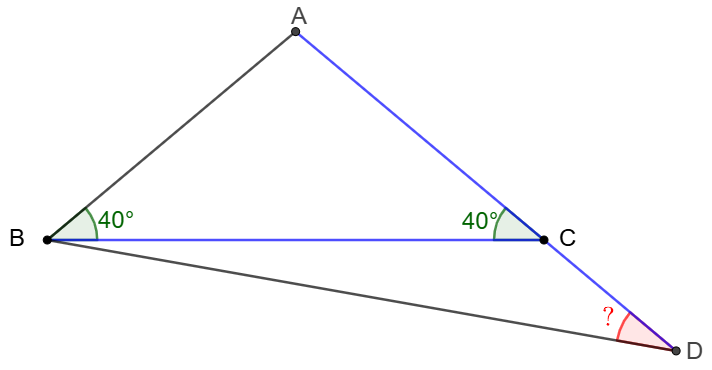
Solve:
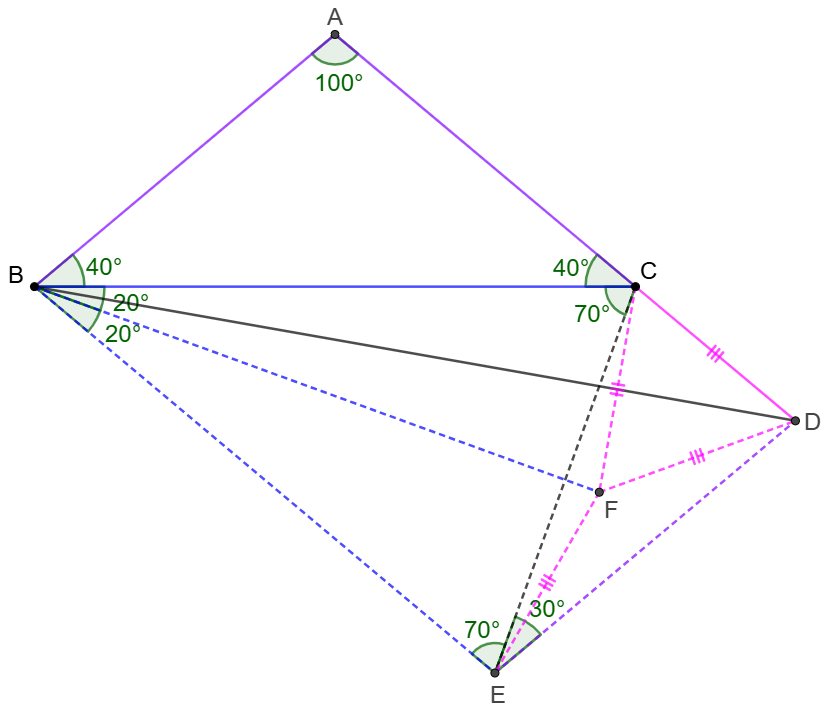 \(\begin{multline}
\shoveleft \text{Get }E \text{ such that }ABED \text{ is a parallelogram} \implies \\
\shoveleft \angle{BED}=\angle{A}=100^{\circ}, \angle{CBE}=\angle{ACB}=40^{\circ}\\
\shoveleft BC=AD=BE \implies \angle{BCE}=\angle{BEC}=70^{\circ}\\
\shoveleft \implies \angle{CED}=30^{\circ},\angle{CDE}=80^{\circ}, \angle{ECD}=70^{\circ}\\
\shoveleft \text{Let } F \text{ be the circumcenter of }\triangle{CDE}\implies\\
\shoveleft EF=CF=DF,\angle{CFD}=60^{\circ}\implies \triangle{CDF}\text{ is equilateral}\\
\shoveleft \implies CD=DF, \angle{FEC}=\angle{FCE}=10^{\circ}\implies BE=BF=BC\\
\shoveleft \implies \triangle{BCD}\cong\triangle{BFD}\implies \angle{ADB}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Get }E \text{ such that }ABED \text{ is a parallelogram} \implies \\
\shoveleft \angle{BED}=\angle{A}=100^{\circ}, \angle{CBE}=\angle{ACB}=40^{\circ}\\
\shoveleft BC=AD=BE \implies \angle{BCE}=\angle{BEC}=70^{\circ}\\
\shoveleft \implies \angle{CED}=30^{\circ},\angle{CDE}=80^{\circ}, \angle{ECD}=70^{\circ}\\
\shoveleft \text{Let } F \text{ be the circumcenter of }\triangle{CDE}\implies\\
\shoveleft EF=CF=DF,\angle{CFD}=60^{\circ}\implies \triangle{CDF}\text{ is equilateral}\\
\shoveleft \implies CD=DF, \angle{FEC}=\angle{FCE}=10^{\circ}\implies BE=BF=BC\\
\shoveleft \implies \triangle{BCD}\cong\triangle{BFD}\implies \angle{ADB}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
11/20/2024
1996 USAMO Problem 5 Let $ABC$ be a triangle, and $M$ an interior point such that $\angle{MAB}=10^{\circ}$, $\angle{MBA}=20^{\circ}$, $\angle{MAC}=40^{\circ}$ and $\angle{MCA}=30^{\circ}$. Prove that the triangle is isosceles.
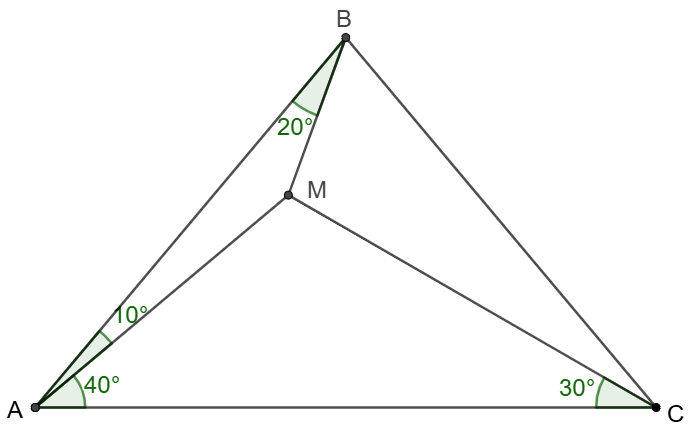
Prove:
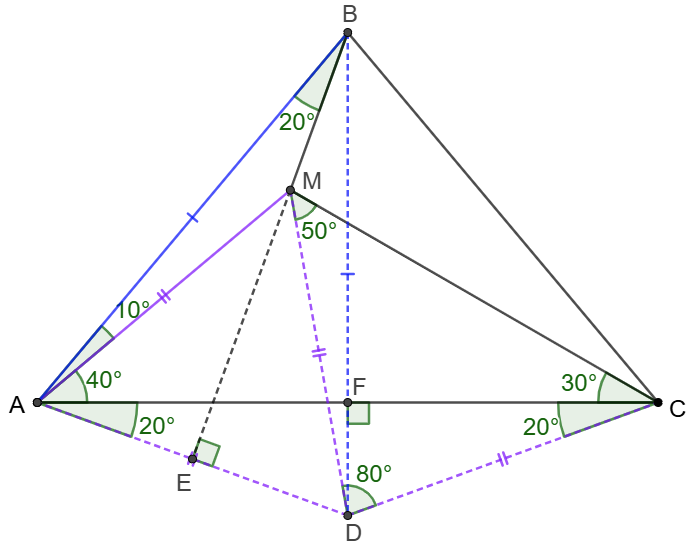 \(\begin{multline}
\shoveleft \text{Let }D \text{ be the circumcenter of }\triangle{ACM} \implies \\
\shoveleft \text{(1)} \angle{ADM}=2\angle{MCA}=60^{\circ} \implies \triangle{ADM} \text{ is equilateral}\\
\shoveleft \implies AM=MD=DA\\
\shoveleft \text{(2) }AD=CD=MD, \angle{CDM}=2\angle{MAC}=80^{\circ}\\
\shoveleft \implies \angle{DCM}=\angle{DMC}=50^{\circ} \implies \angle{DAC}=\angle{DCA}=20^{\circ}\\
\shoveleft \implies \angle{BAD}=70^{\circ} \implies BM\perp AD \implies\text{Let }E=AD\cap BM\\
\shoveleft AE=DE\implies \triangle{BAE}\cong\triangle{BDE}\implies \angle{MDB}=\angle{MBA}=10^{\circ}\\
\shoveleft \implies \angle{BDC}=70^{\circ} \implies BD \perp AC \implies \text{Let }F=AC\cap BD\\
\shoveleft \angle{DFC}=90^{\circ}\implies \triangle{ADF}\cong\triangle{CDF}\implies AF=CF\\
\shoveleft \implies \triangle{ABF}\cong\triangle{CBF}\implies AB=BC \blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }D \text{ be the circumcenter of }\triangle{ACM} \implies \\
\shoveleft \text{(1)} \angle{ADM}=2\angle{MCA}=60^{\circ} \implies \triangle{ADM} \text{ is equilateral}\\
\shoveleft \implies AM=MD=DA\\
\shoveleft \text{(2) }AD=CD=MD, \angle{CDM}=2\angle{MAC}=80^{\circ}\\
\shoveleft \implies \angle{DCM}=\angle{DMC}=50^{\circ} \implies \angle{DAC}=\angle{DCA}=20^{\circ}\\
\shoveleft \implies \angle{BAD}=70^{\circ} \implies BM\perp AD \implies\text{Let }E=AD\cap BM\\
\shoveleft AE=DE\implies \triangle{BAE}\cong\triangle{BDE}\implies \angle{MDB}=\angle{MBA}=10^{\circ}\\
\shoveleft \implies \angle{BDC}=70^{\circ} \implies BD \perp AC \implies \text{Let }F=AC\cap BD\\
\shoveleft \angle{DFC}=90^{\circ}\implies \triangle{ADF}\cong\triangle{CDF}\implies AF=CF\\
\shoveleft \implies \triangle{ABF}\cong\triangle{CBF}\implies AB=BC \blacksquare
\end{multline}\)
11/21/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=16^{\circ}$, $\angle{CBD}=14^{\circ}$, $\angle{BCD}=14^{\circ}$, $\angle{ACD}=32^{\circ}$. Find $\angle{ADB}$.
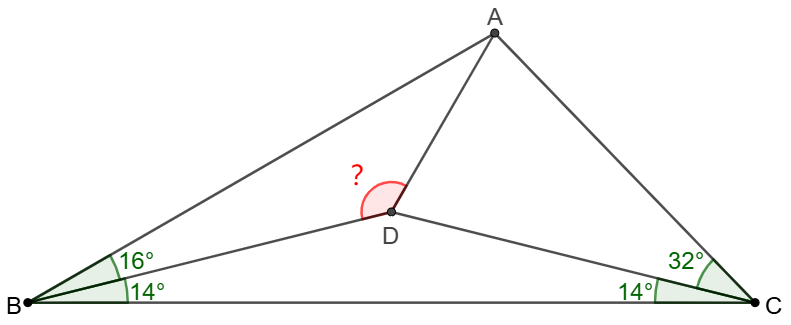
Solve:
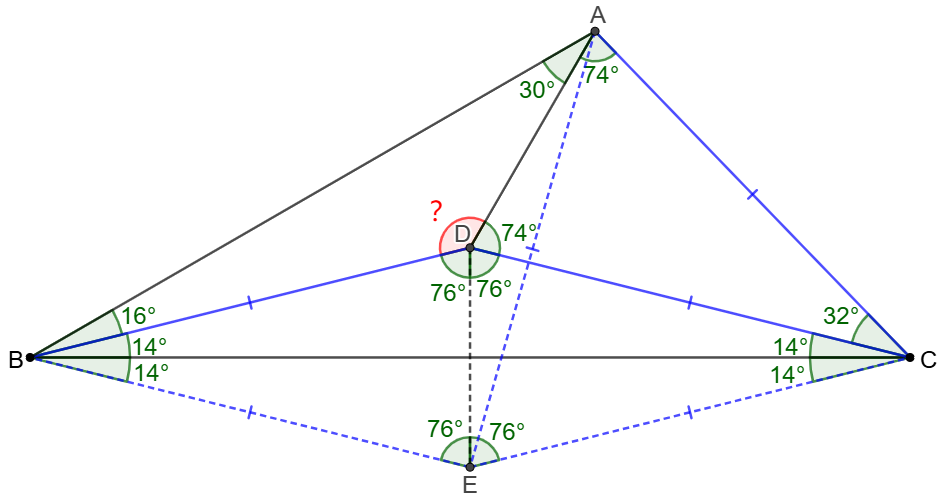 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC} \implies\\
\shoveleft \text{(1) } EA=EB=EC, \angle{AEC}=2\angle{ABC}=60^{\circ}\\
\shoveleft \implies \triangle{AEC} \text{ is equilateral} \implies AE=CE=AC\\
\shoveleft \angle{ACE}=\angle{CAE}=60^{\circ}\implies\\
\shoveleft \angle{BCE}=\angle{BEC}=14^{\circ}=\angle{BCD}=\angle{CBD}\\
\shoveleft \implies E \text{ is the reflection of }D \text{ along }BC\implies\\
\shoveleft \angle{CDE}=\angle{CED}=\angle{BDE}=\angle{BED}=76^{\circ}\\
\shoveleft BE=CE=BD=CD=AC \implies \\
\shoveleft \angle{CAD}=\angle{CDA}=\dfrac{180^{\circ}-32^{\circ}}{2}= 74^{\circ}\\
\shoveleft \implies \angle{ADB}=360^{\circ}-76^{\circ}-76^{\circ}-74^{\circ}=\bbox[5px, border: 1px solid black]{134^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC} \implies\\
\shoveleft \text{(1) } EA=EB=EC, \angle{AEC}=2\angle{ABC}=60^{\circ}\\
\shoveleft \implies \triangle{AEC} \text{ is equilateral} \implies AE=CE=AC\\
\shoveleft \angle{ACE}=\angle{CAE}=60^{\circ}\implies\\
\shoveleft \angle{BCE}=\angle{BEC}=14^{\circ}=\angle{BCD}=\angle{CBD}\\
\shoveleft \implies E \text{ is the reflection of }D \text{ along }BC\implies\\
\shoveleft \angle{CDE}=\angle{CED}=\angle{BDE}=\angle{BED}=76^{\circ}\\
\shoveleft BE=CE=BD=CD=AC \implies \\
\shoveleft \angle{CAD}=\angle{CDA}=\dfrac{180^{\circ}-32^{\circ}}{2}= 74^{\circ}\\
\shoveleft \implies \angle{ADB}=360^{\circ}-76^{\circ}-76^{\circ}-74^{\circ}=\bbox[5px, border: 1px solid black]{134^{\circ}}
\end{multline}\)
11/22/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=12^{\circ}$, $\angle{CBD}=30^{\circ}$, $\angle{BCD}=18^{\circ}$, $\angle{ACD}=24^{\circ}$. Find $\angle{ADB}$.
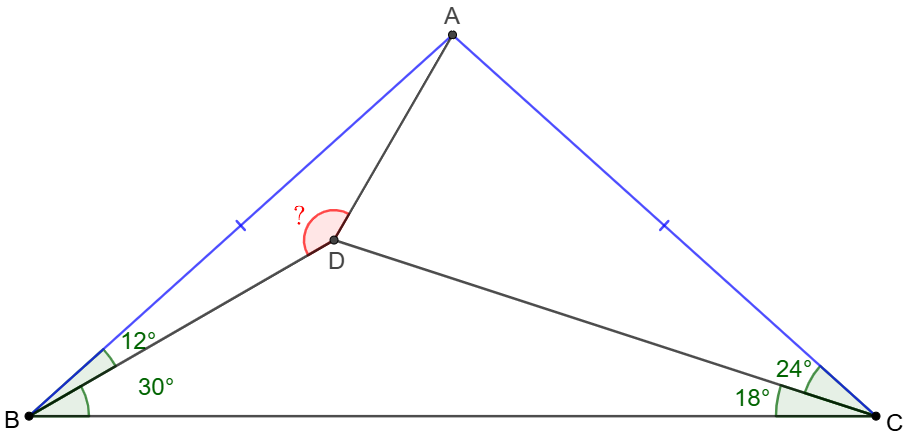
Solve:
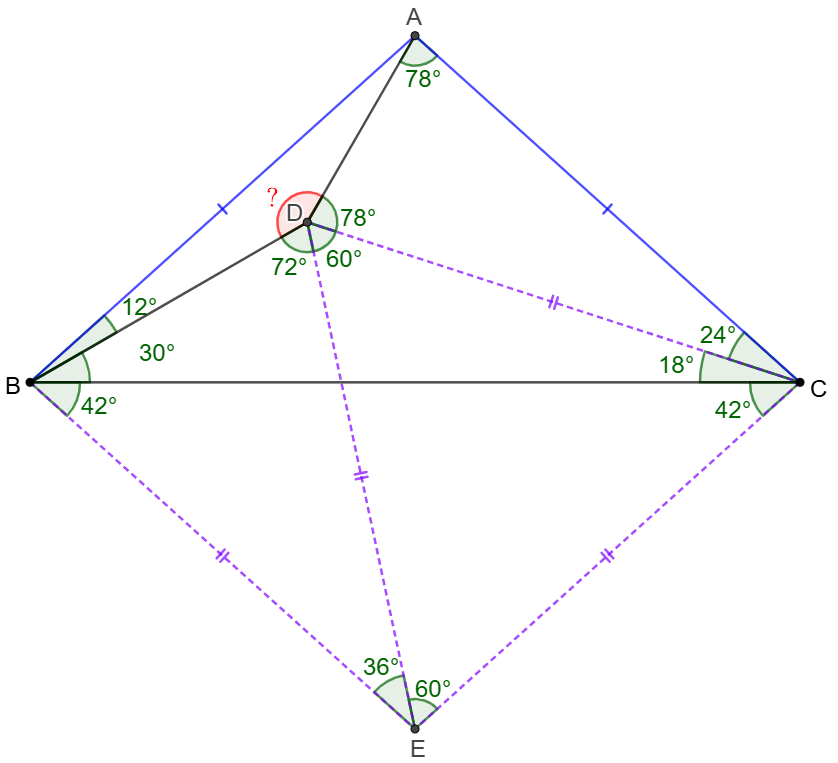 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{BCD} \implies\\
\shoveleft \text{(1) }BE=CE=DE, \angle{CED}=2\angle{CBD}=60^{\circ}\\
\shoveleft \implies \triangle{CDE} \text{ is equilateral}\implies\\
\shoveleft BE=CE=DE=CD, \angle{CDE}=\angle{CED}=60^{\circ}\\
\shoveleft \text{(2) }\angle{BED}=2\angle{BCE}=36^{\circ}\implies\\
\shoveleft \angle{BDE}=\angle{DBE}=72^{\circ}\implies\\
\shoveleft \angle{EBC}=\angle{ECB}=42^{\circ}=\angle{ACB}=\angle{ABC}\\
\shoveleft \implies ABEC \text{ is a rhomb }\implies CD=CE=AC\\
\shoveleft \implies \angle{ADC}=\angle{DAC}=\dfrac{180^{\circ}-32^{\circ}}{2}=78^{\circ}\\
\shoveleft \implies \angle{ADB}360^{\circ}-72^{\circ}-60^{\circ}-78^{\circ}=\bbox[5px, border: 1px solid black]{150^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{BCD} \implies\\
\shoveleft \text{(1) }BE=CE=DE, \angle{CED}=2\angle{CBD}=60^{\circ}\\
\shoveleft \implies \triangle{CDE} \text{ is equilateral}\implies\\
\shoveleft BE=CE=DE=CD, \angle{CDE}=\angle{CED}=60^{\circ}\\
\shoveleft \text{(2) }\angle{BED}=2\angle{BCE}=36^{\circ}\implies\\
\shoveleft \angle{BDE}=\angle{DBE}=72^{\circ}\implies\\
\shoveleft \angle{EBC}=\angle{ECB}=42^{\circ}=\angle{ACB}=\angle{ABC}\\
\shoveleft \implies ABEC \text{ is a rhomb }\implies CD=CE=AC\\
\shoveleft \implies \angle{ADC}=\angle{DAC}=\dfrac{180^{\circ}-32^{\circ}}{2}=78^{\circ}\\
\shoveleft \implies \angle{ADB}360^{\circ}-72^{\circ}-60^{\circ}-78^{\circ}=\bbox[5px, border: 1px solid black]{150^{\circ}}
\end{multline}\)
11/23/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=24^{\circ}$, $\angle{CBD}=26^{\circ}$, $\angle{ACD}=10^{\circ}$, $\angle{BCD}=28^{\circ}$. Find $\angle{BAD}$.
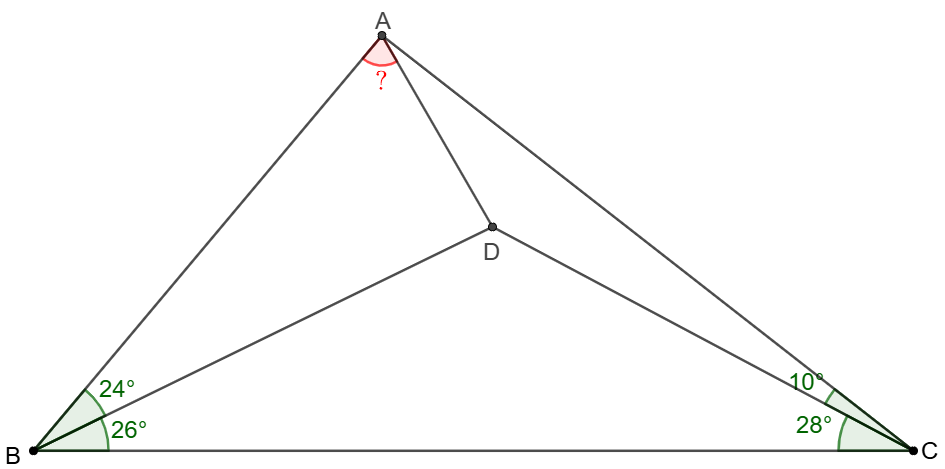
Solve:
11/24/2024
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=24^{\circ}$, $\angle{CBD}=6^{\circ}$, $\angle{ACD}=12^{\circ}$, $\angle{BCD}=6^{\circ}$. Find $\angle{CAD}$.
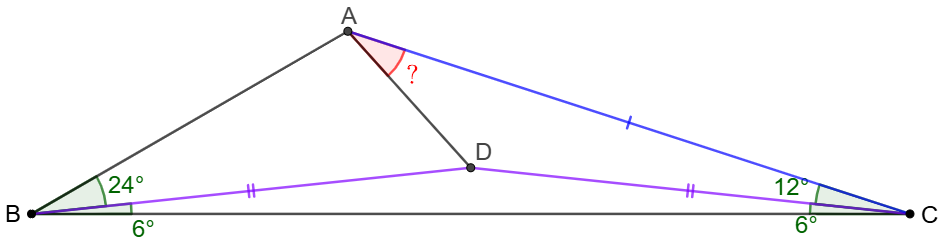
Solve:
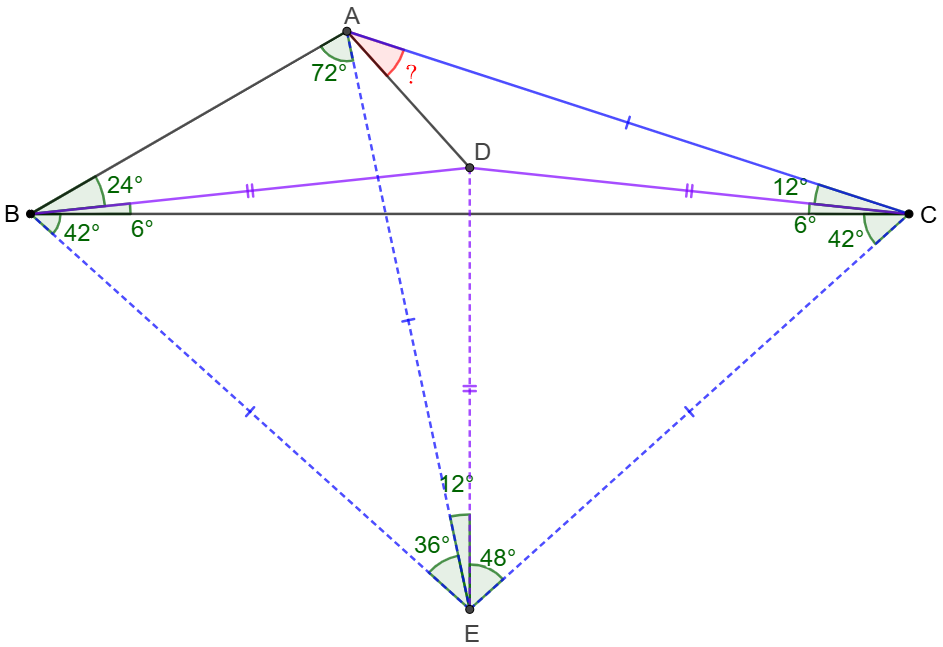 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC}\implies\\
\shoveleft \text{(1) }AE=BC=CE, \angle{AEB}=2\angle{ACB}=36^{\circ}\\
\shoveleft \implies \angle{ABE}=\angle{BAE}=72^{\circ} \implies \angle{EBC}=\angle{ECB}=42^{\circ}\\
\shoveleft \implies \angle{BEC}=96^{\circ}\\
\shoveleft BD=CD \implies \triangle{BDE}\cong\triangle{CDE}\implies\\
\shoveleft \angle{BED}=\angle{CED}=48^{\circ}=\angle{DBE}=\angle{DCE} \implies \\
\shoveleft BD=CD=DE\\
\shoveleft \text{(2) }\angle{AEC}=2\angle{ABC}=60^{\circ}\implies \triangle{AEC} \text{ is equilateral}\\
\shoveleft \implies AC=CE=EA=EB \implies \triangle{ADE}\cong\triangle{ADC}\\
\shoveleft \implies \angle{CAD}=\angle{EAD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of }\triangle{ABC}\implies\\
\shoveleft \text{(1) }AE=BC=CE, \angle{AEB}=2\angle{ACB}=36^{\circ}\\
\shoveleft \implies \angle{ABE}=\angle{BAE}=72^{\circ} \implies \angle{EBC}=\angle{ECB}=42^{\circ}\\
\shoveleft \implies \angle{BEC}=96^{\circ}\\
\shoveleft BD=CD \implies \triangle{BDE}\cong\triangle{CDE}\implies\\
\shoveleft \angle{BED}=\angle{CED}=48^{\circ}=\angle{DBE}=\angle{DCE} \implies \\
\shoveleft BD=CD=DE\\
\shoveleft \text{(2) }\angle{AEC}=2\angle{ABC}=60^{\circ}\implies \triangle{AEC} \text{ is equilateral}\\
\shoveleft \implies AC=CE=EA=EB \implies \triangle{ADE}\cong\triangle{ADC}\\
\shoveleft \implies \angle{CAD}=\angle{EAD}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
11/25/2024
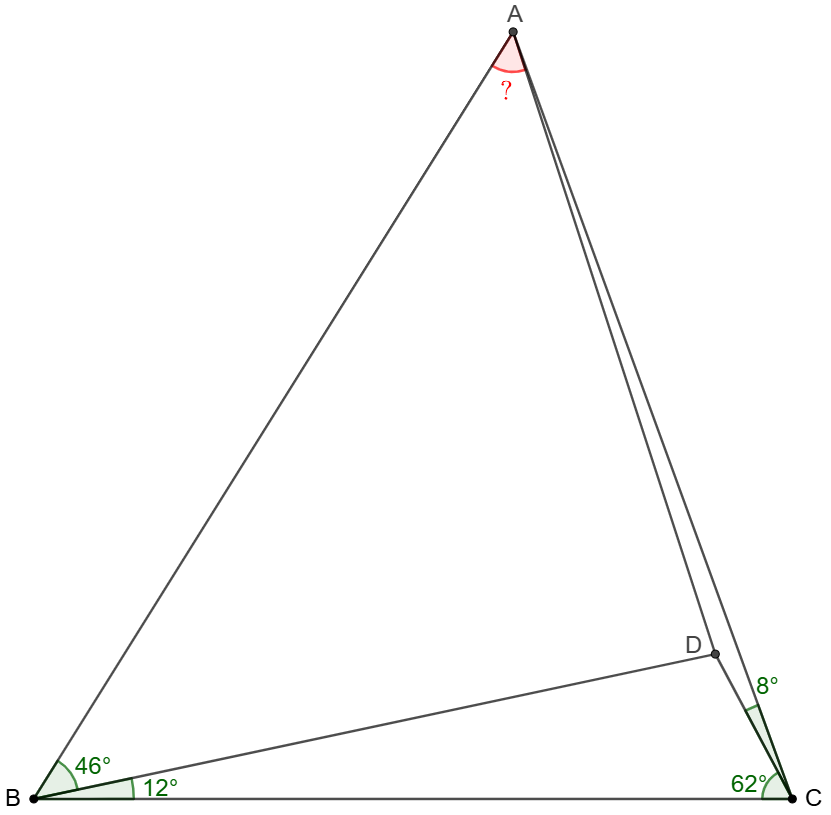
Point $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=46^{\circ}$, $\angle{CBD}=12^{\circ}$, $\angle{ACD}=8^{\circ}$, $\angle{BCD}=62^{\circ}$. Find $\angle{BAD}$.
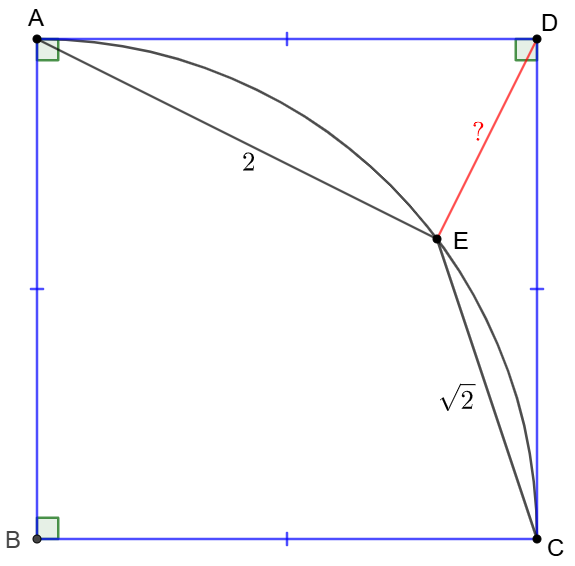
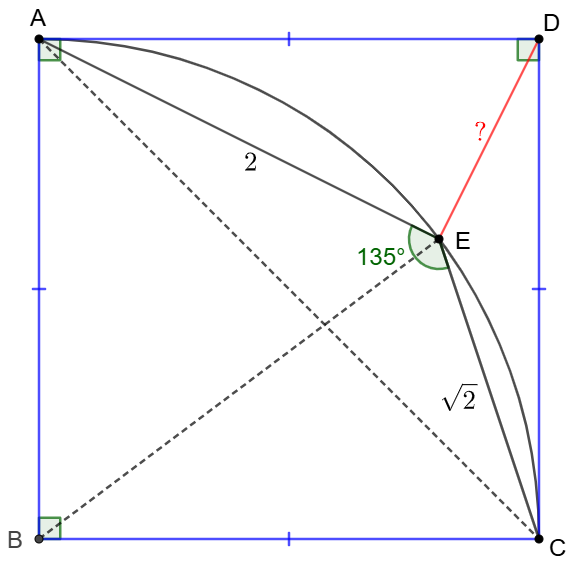
11/27/2024
$E$ is inside square $ABCD$ and is on the circle $\odot{B}$ with radius of the side of the square. $AE=2, CE=\sqrt{2}$, find $DE$
Solve:
 \(\begin{multline}
\shoveleft \text{Easy to see that }\angle{AEC}=180^{\circ}-\dfrac{\angle{ABC}}{2}=135^{\circ}\\
\shoveleft \implies AC=\sqrt{AE^2+CE^2-2AE\cdot CE\cdot cos135^{\circ}}\\
\shoveleft =\sqrt{4+2-2\cdot 2\cdot\sqrt{2}\cdot(-\dfrac{\sqrt{2}}{2})}=\sqrt{10}\\
\shoveleft \implies BE=AB=\sqrt{5}\\
\shoveleft \href{https://en.wikipedia.org/wiki/British_flag_theorem}{\text{British Flag Theorem}} \implies AE^2+CE^2=BE^2+DE^2\\
\shoveleft \implies DE^2=4+2-5=1\implies DE=\bbox[5px, border: 1px solid black]{1}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Easy to see that }\angle{AEC}=180^{\circ}-\dfrac{\angle{ABC}}{2}=135^{\circ}\\
\shoveleft \implies AC=\sqrt{AE^2+CE^2-2AE\cdot CE\cdot cos135^{\circ}}\\
\shoveleft =\sqrt{4+2-2\cdot 2\cdot\sqrt{2}\cdot(-\dfrac{\sqrt{2}}{2})}=\sqrt{10}\\
\shoveleft \implies BE=AB=\sqrt{5}\\
\shoveleft \href{https://en.wikipedia.org/wiki/British_flag_theorem}{\text{British Flag Theorem}} \implies AE^2+CE^2=BE^2+DE^2\\
\shoveleft \implies DE^2=4+2-5=1\implies DE=\bbox[5px, border: 1px solid black]{1}
\end{multline}\)
11/28/2024
$\angle{ABC}=15^{\circ}$ in $\triangle{ABC}$, $D$ is the midpoint of $BC$ and $\angle{BAD}=30^{\circ}$, find $\angle{ACB}$.
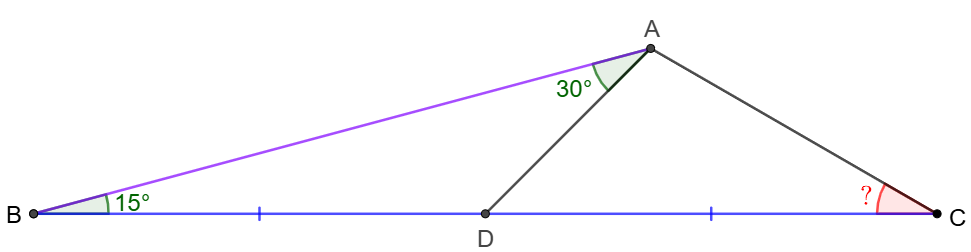
Solve:
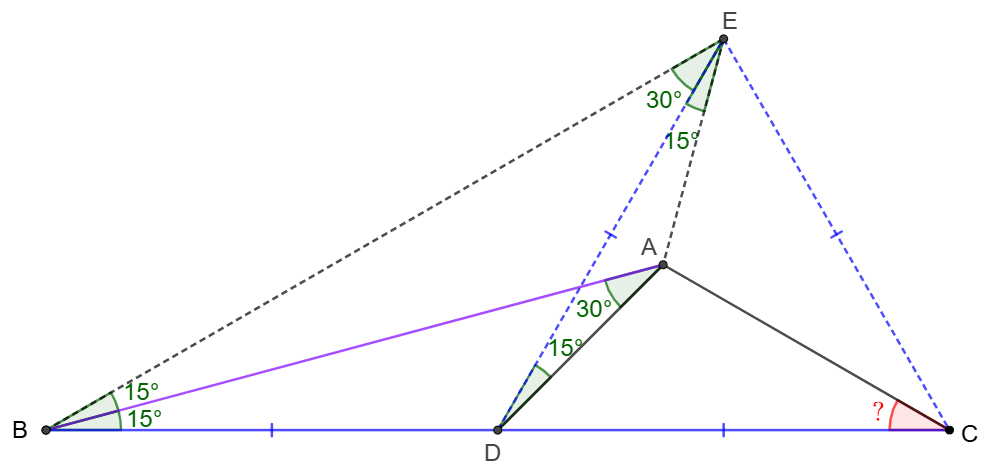 \(\begin{multline}
\shoveleft \text{Let }E \text{ on the same side of }BC \text{ as } A \text{ such that }\triangle{CDE}\text{ is equilateral}\\
\shoveleft \implies CD=DE=CE=BD, \angle{DCE}=\angle{CDE}=60^{\circ}\\
\shoveleft \implies \angle{ADE}=15^{\circ}, \angle{DBE}=\angle{DEB}=30^{\circ}=\angle{BAD}\\
\shoveleft \implies ADBE \text{ is cyclic}\implies \angle{AED}=\angle{ABD}=15^{\circ}\implies AD=AE\\
\shoveleft \implies \triangle{ACD}\cong\triangle{ACE}\implies \angle{ACB}=\angle{ACE}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ on the same side of }BC \text{ as } A \text{ such that }\triangle{CDE}\text{ is equilateral}\\
\shoveleft \implies CD=DE=CE=BD, \angle{DCE}=\angle{CDE}=60^{\circ}\\
\shoveleft \implies \angle{ADE}=15^{\circ}, \angle{DBE}=\angle{DEB}=30^{\circ}=\angle{BAD}\\
\shoveleft \implies ADBE \text{ is cyclic}\implies \angle{AED}=\angle{ABD}=15^{\circ}\implies AD=AE\\
\shoveleft \implies \triangle{ACD}\cong\triangle{ACE}\implies \angle{ACB}=\angle{ACE}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)