M∀TH Workout

October 2024

 
  • Oct 04, 2024

10/04/2024

$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=6^{\circ}$, $\angle{BAD}=30^{\circ}$, $\angle{CAD}=54^{\circ}$, $\angle{ACD}=24^{\circ}$, find $\angle{CBD}$.

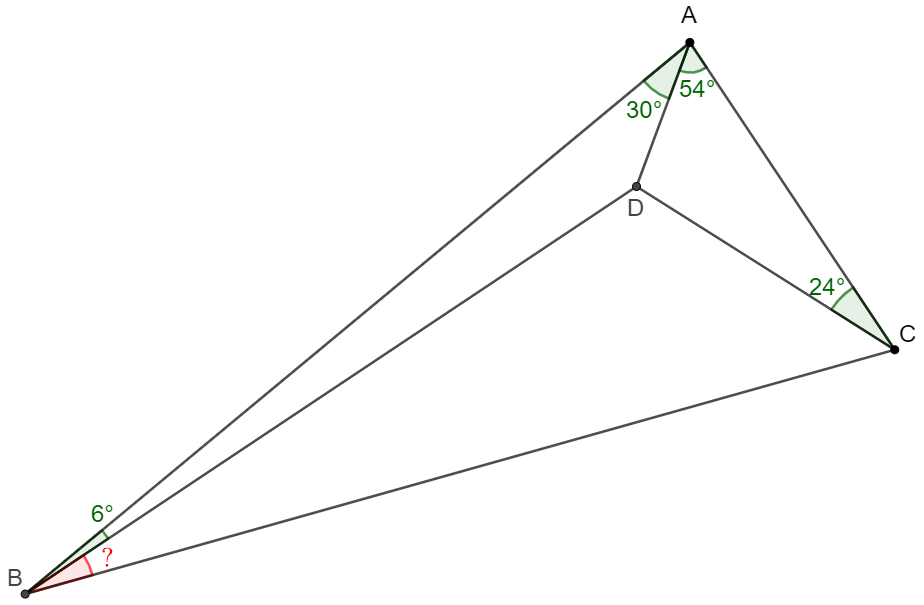
image-20241004050430794

Solve:

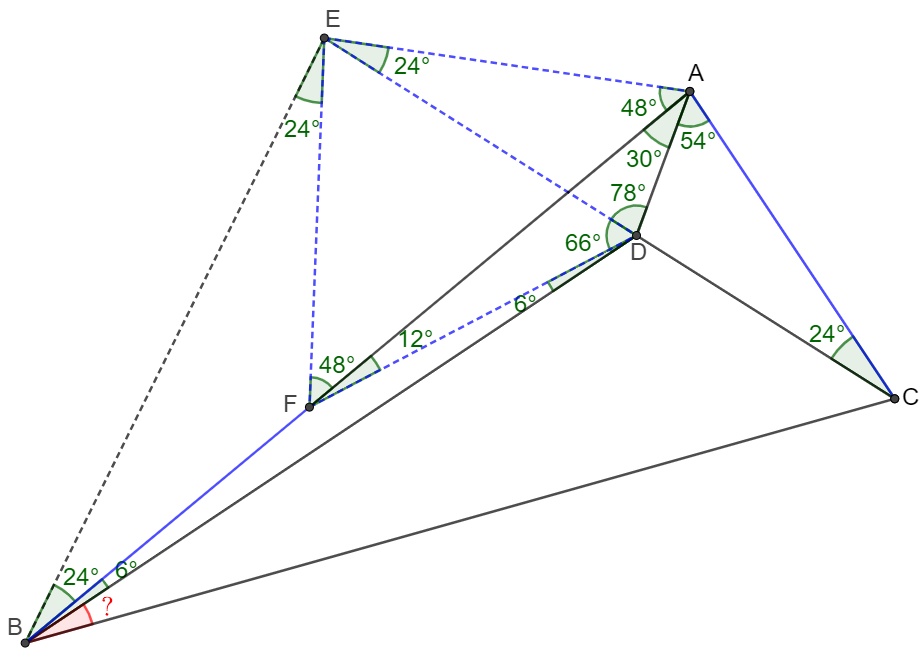image-20241005044451477 \(\begin{multline} \shoveleft \text{Extend }CD \text{ to }E \text{ such that }AC=AE \implies \angle{AEC}=\angle{ACE}=24^{\circ}, \angle{EAB}=48^{\circ}\\ \shoveleft \implies \angle{EDA}=78^{\circ}=\angle{EAD}\implies EA=ED=AC, \angle{EDB}=66^{\circ}\\ \shoveleft \text{Let }F \text{ on }AB \text{ such that }\angle{DEF}=60^{\circ}\implies \angle{AEF}=84^{\circ}\implies \angle{AFE}=48^{\circ}=\angle{EAB}\\ \shoveleft \implies EF=EA=ED\implies \triangle{DEF}\text{ is equilateral}\implies \angle{EFD}=\angle{EDF}=60^{\circ}\\ \shoveleft DF=EF=DE=EA=AC\implies \angle{AFD}=12^{\circ}\implies \angle{BDF}=6^{\circ}=\angle{ABD}\\ \shoveleft \implies BF=DF=EF\implies \angle{EBF}=\angle{BEF}=24^{\circ}=\angle{ACD}\implies ACBE\text{ is cyclic}\\ \shoveleft \implies \angle{ABC}=\angle{AEC}=24^{\circ}\implies \angle{CBD}=24^{\circ}-6^{\circ}=\bbox[5px, border: 1px solid black]{18^{\circ}} \end{multline}\)

10/06/2024

$D$ is a point inside $\triangle{ABC}$ such that $\angle{BAD}=20^{\circ}$, $\angle{CAD}=30^{\circ}$, $\angle{ACD}=40^{\circ}$, $\angle{BCD}=10^{\circ}$, find $\angle{CBD}$.

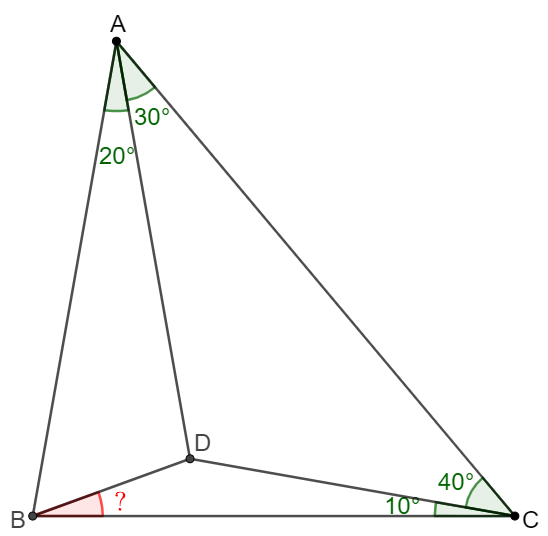
image-20241006213056781

Solve:

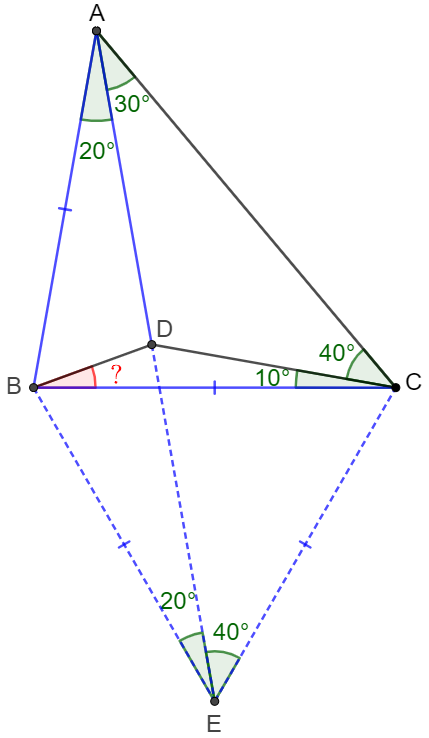image-20241006212924216 \(\begin{multline} \shoveleft \angle{BAC}=50^{\circ}=\angle{BCA}\implies AB=BC, \angle{ABC}=80^{\circ}\\ \shoveleft \text{Extend }AD \text{ to }E \text{ such that }AB=BE\implies \angle{BEA}=\angle{BAE}=20^{\circ}\\ \shoveleft \implies \angle{ABE}=140^{\circ}\implies \angle{EBC}=60^{\circ}\\ \shoveleft AB=BE=BC\implies \triangle{BCE} \text{ is equilateral} \implies BE=EC=BC=AE\\ \shoveleft \angle{BEC}=60^{\circ}=\angle{BCE}\implies \angle{DEC}=40^{\circ},\angle{DCE}=70^{\circ}\\ \shoveleft \implies \angle{CDE}=70^{\circ}=\angle{DCE}\implies CE=DE=BE\implies \angle{DBE}=80^{\circ}\\ \shoveleft \implies \angle{CBD}=\angle{DBE}-\angle{EBC}=\bbox[5px, border: 1px solid black]{20^{\circ}} \end{multline}\)

10/07/2024

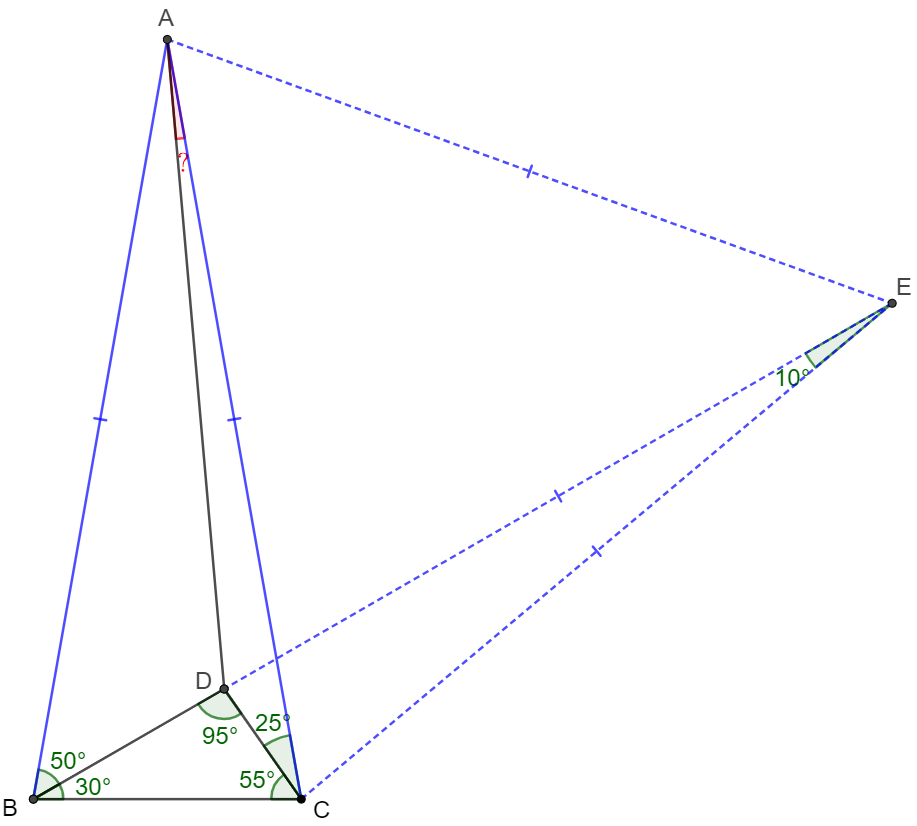
$\triangle{ABC}$ is an isosceles triangle with $AB=AC$, $\angle{ABC}=\angle{ACB}=80^{\circ}$, $D$ is inside $\triangle{ABC}$ such that $\angle{ABD}=50^{\circ}$, $\angle{ACD}=25^{\circ}$ , find $\angle{CAD}$.

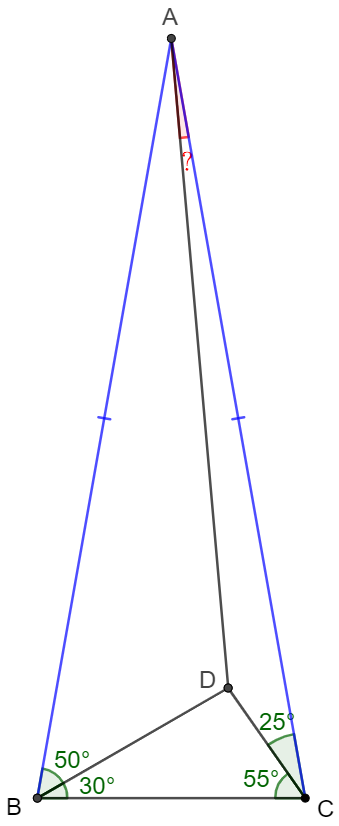
image-20241011010646279

Solve:

image-20241011005649038

\[\begin{multline} \shoveleft AB=AC\implies \angle{ABC}=\angle{ABC}=80^{\circ}\implies \angle{BAC}=20^{\circ}\\ \shoveleft \text{Extend } BD \text{ to }E \text{ such that }AB=AE \implies\\ \shoveleft \angle{ABE}=\angle{AEB}=50^{\circ}, \angle{BAE}=80^{\circ} \implies \\ \shoveleft \angle{CAE}=60^{\circ}\implies \triangle{CAE} \text{ is equilateral} \implies\\ \shoveleft \angle{ACE}=\angle{AEC}=60^{\circ}\implies \angle{BEC}=10^{\circ}, \angle{ECD}=85^{\circ}=\angle{EDC}\\ \shoveleft \implies EC=ED=AE, \angle{AED}=50^{\circ}\implies \angle{ADE}=\angle{DAE}=65^{\circ}\\ \shoveleft \implies \angle{CAD}=\angle{DAE}-60^{\circ}=\bbox[5px, border: 1px solid black]{5^{\circ}} \end{multline}\]

10/13/2024

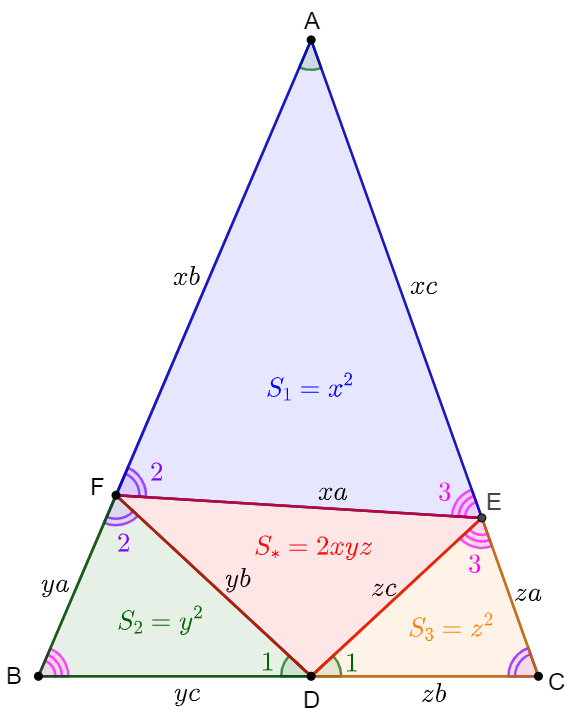
$D,E,F$ are on side $BC, CA, AB$ of $\triangle{ABC}$ respectively such that $\angle{AFE}=\angle{BFD}$, $\angle{AEF}=\angle{CED}$, $\angle{BDF}=\angle{CDE}$, and $[AEF]=5$,$[BDF]=2$, $[CDE]=1$, find $[DEF]$.

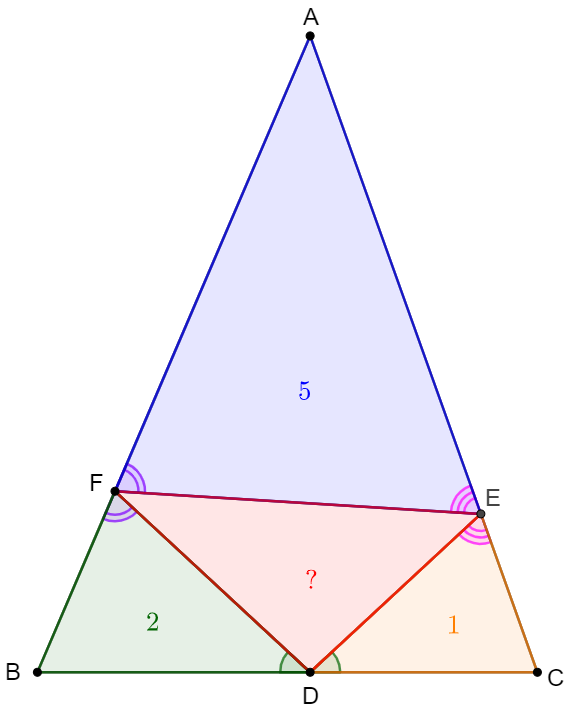
image-20241013233405056

Solve:

image-20241013234635489 \(\begin{multline} \shoveleft \text{Let } \angle{BDF}=\angle{CDE}=\angle{1}, \angle{AFE}=\angle{BFD}=\angle{2}, \angle{AEF}=\angle{CED}=\angle{3}\\ \shoveleft \implies \angle{A}+\angle{2}+\angle{3}=180^{\circ},\angle{B}+\angle{1}+\angle{2}=180^{\circ}, \angle{C}+\angle{1}+\angle{3}=180^{\circ}\\ \shoveleft \implies 2(\angle{1}+\angle{2}+\angle{3})=360^{\circ}\implies \angle{1}+\angle{2}+\angle{3}=180^{\circ}\\ \shoveleft \implies \angle{A}=\angle{1}, \angle{B}=\angle{3}, \angle{C}=\angle{2} \implies \triangle{AFE}\sim\triangle{DFB}\sim\triangle{DCE}\sim\triangle{ACB}\\ \shoveleft \text{Let }x=\sqrt{\dfrac{[DEC]}{[ABC]}}, y=\sqrt{\dfrac{[DBF]}{[ABC]}}, z=\sqrt{\dfrac{[AEF]}{[ABC]}}, AB=c, BC=a, CA=b \implies\\ \shoveleft EF=xa, AF=xb, AE=xc, FB=ya, DF=yb, BD=yc, EC=za, CD=zb, DE=zc\\ \shoveleft \implies BD+DC=BC=yc+zb=a \implies c=\dfrac{1}{y}a-\dfrac{z}{y}b\\ \shoveleft AE+EC=AC=xc+za=b \implies (\dfrac{x}{y}+z)a = (1+\dfrac{xz}{y})b\\ \shoveleft AF+FB=AB=xb+ya=c \implies (\dfrac{1}{y}-y)a=(x+\dfrac{z}{y})b\\ \shoveleft \implies \dfrac{x+yz}{1-y^2}=\dfrac{y+xz}{xy+z} \implies x^2+y^2+z^2+2xyz=1\\ \shoveleft \text{Since }x^2+y^2+z^2+\dfrac{[DEF]}{[ABC]}=1 \implies \dfrac{[DEF]}{[ABC]}=2xyz\\ \shoveleft \text{Let }s=[ABC], s_1=[AEF], s_2=[BDF], s_3=[DEC]\\ \shoveleft \implies 2\sqrt{\dfrac{s_1s_2s_3}{s^3}}=1-\dfrac{s_1+s_2+s_3}{s}\\ \shoveleft \implies s^3-2(s_1+s_2+s_3)s^2+(s_1+s_2+s_3)s-4s_1s_2s_3=0\\ \shoveleft \text{Let }m=s_1+s_2+s_3, n=s_1s_2s_3 \implies s^3-2ms^2+m^2s-4n=0\\ \shoveleft \implies s = \dfrac{\sqrt[3]{6 \sqrt{81 n^2 - 3m^3n} - m^3 + 54 n} + m)^2} {3 \sqrt[3]{6 \sqrt{81 n^2 - 3m^3n} - m^3 + 54 n}}\\ \shoveleft \text{When }m=1+2+5, n=1*2*5, s=10, 3\pm\sqrt{5} \text{ (removed)}\\ \shoveleft \implies [ABC]=10 \implies [DEF]=10-8=\bbox[5px, border: 1px solid black]{2} \end{multline}\)

10/15/2024

$M$ is the midpoint of side $BC$ of $\triangle{ABC}$, and $D$ is a point on the circumcircle of $\triangle{ABC}$ such that $\angle{MAC}=\angle{BAD}$. $X,Y,Z$ are perpendicular feet from $D$ to $BC, AC, AB$ respectively. Prove: $XY=XZ$.

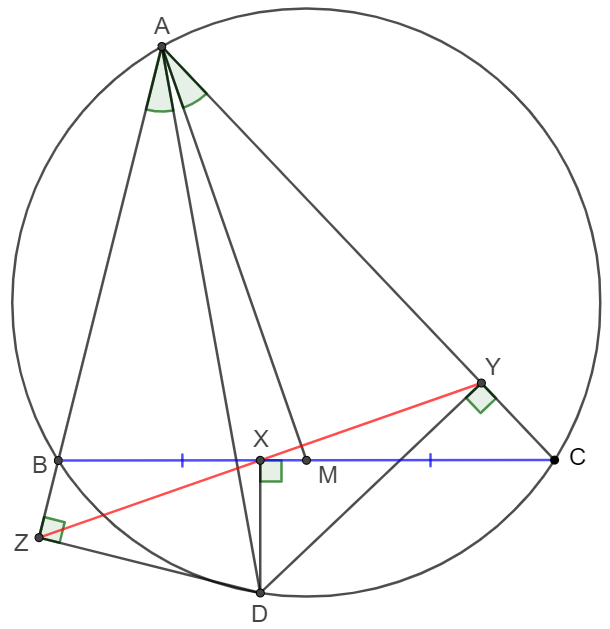
image-20241015023220107

Prove:

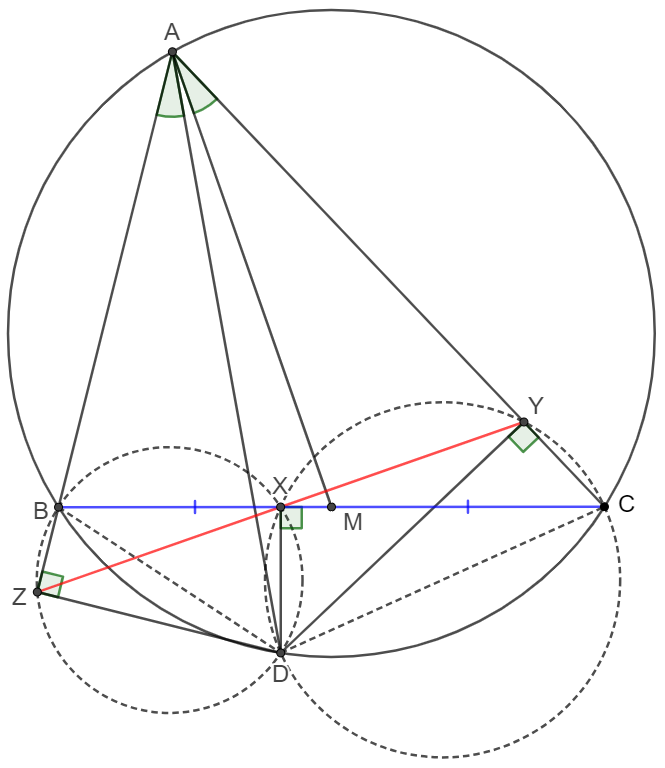image-20241015023100326 \(\begin{multline} \shoveleft AD \text{ is the A-symmedian of } \triangle{ABC} \implies \dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{sin\angle{ACB}}{sin\angle{ABC}}\\ \shoveleft \implies BD \cdot sin{\angle{ABC}}=CD \cdot sin{\angle{ACB}}\\ \shoveleft DZ\perp BZ, DX \perp BX \implies BXDZ \text{ is cyclic }, BD \text{ is the diameter of }(BXDZ)\\ \shoveleft \implies ZX=BD \cdot sin\angle{XDZ} = BD \cdot sin\angle{ABC}\\ \shoveleft DX \perp XC, DY \perp YC \implies CDXY \text{ is cyclic }, CD \text{ is the diameter of }(CDXY)\\ \shoveleft \implies XY = CD \cdot sin{\angle{XCY}}= CD \cdot sin{\angle{ACB}}= BD \cdot sin\angle{ABC} = ZX \blacksquare\\ \end{multline}\) Note: This proof is given here.

Prove 2:

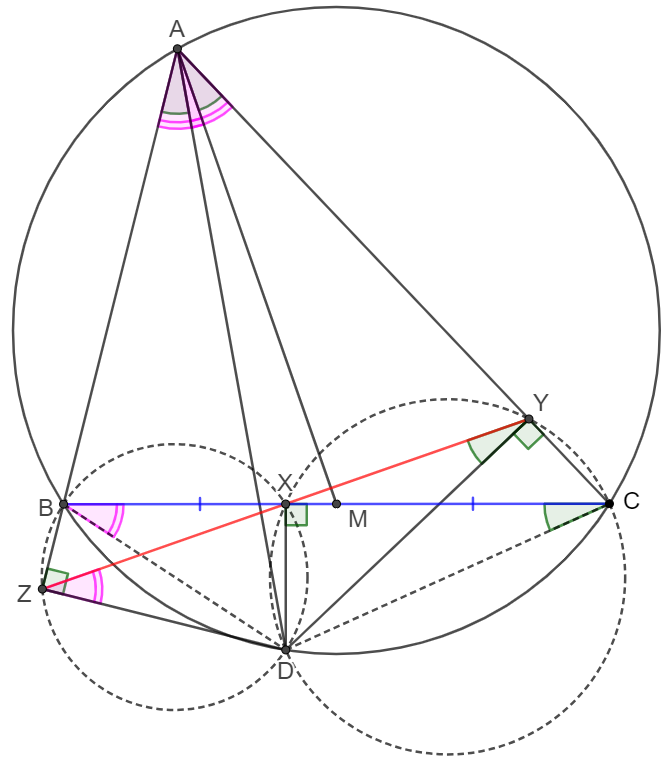image-20241015104547464 \(\begin{multline} \shoveleft DX \perp XC, DY \perp YC \implies CDXY \text{ is cyclic }\\ \shoveleft \implies \angle{MAC}=\angle{BAD}=\angle{XYD}, \angle{ACM}=\angle{XDY}\\ \shoveleft \implies \triangle{ACM}\sim\triangle{YDX}\implies \dfrac{XY}{AM}=\dfrac{XD}{CM}\\ \shoveleft DZ\perp BZ, DX \perp BX \implies BXDZ \text{ is cyclic }\\ \shoveleft \implies \angle{DAC}=\angle{MAC}+\angle{DAM}=\angle{BAD}+\angle{DAM}\\ \shoveleft =\angle{BAM}=\angle{DBC}=\angle{DZX}, \angle{XDZ}=\angle{ABM}\\ \shoveleft \implies \triangle{ABM}\sim\triangle{ZXD}\implies \dfrac{ZX}{AM}=\dfrac{XD}{BM}\\ \shoveleft =\dfrac{XD}{CM}=\dfrac{XY}{AM}\implies XD=XY\blacksquare \end{multline}\)

10/19/2024

asd

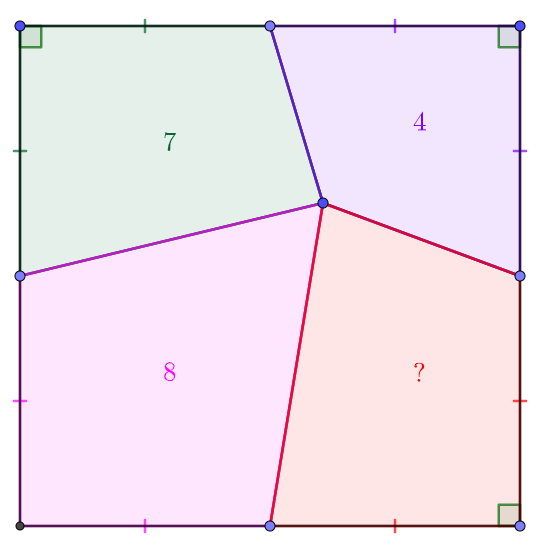
image-20241019054229295

Solve:

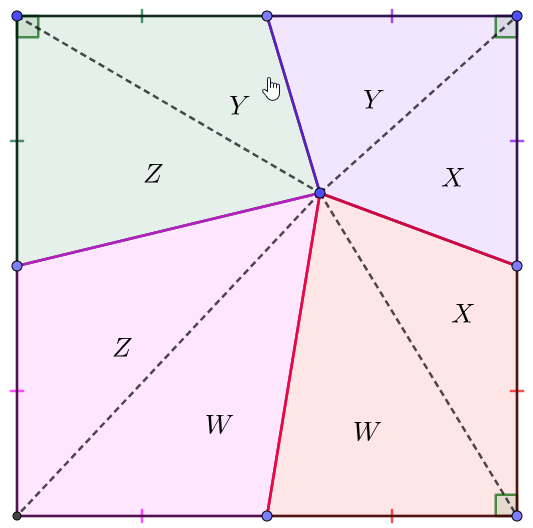image-20241019054506840 \(\begin{multline} \shoveleft X+Y=4, Y+Z=7,Z+W=8 \implies X+Y-Y-Z+Z+W=X+W=4-7+8=\bbox[5px, border: 1px solid black]{5} \end{multline}\)

10/20/2024

$OABC$ and $ODEF$ are squares. Prove that $AD, BE, CF$ are concurrent at one point.

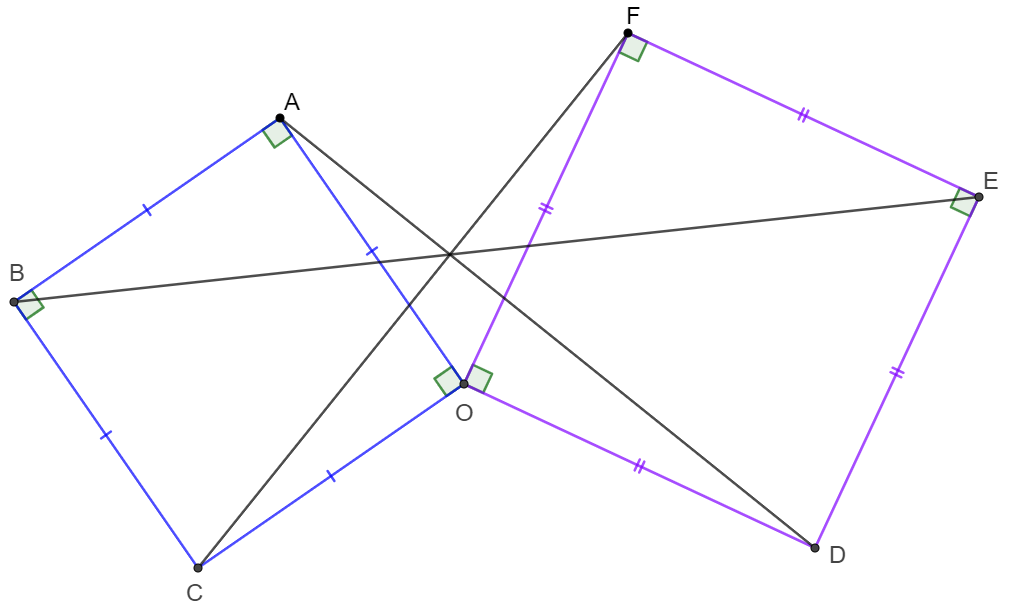
image-20241020185941545

Prove:

image-20241020190419896 \(\begin{multline} \shoveleft \text{Let }AD \cap CF = G \implies \triangle{AOD}\cong\triangle{COF}\\ \shoveleft AO \perp CO \implies AD \perp CF \implies ABCG, DEFG \text{ is cyclic}\\ \shoveleft \implies \angle{AGB}=\angle{ACB}=45^{\circ}, \angle{EGF}=\angle{EDF}=45^{\circ}\\ \shoveleft \implies \angle{BGE}=45^{\circ}+90^{\circ}+45^{\circ}=180^{\circ}\implies BGE \text{ is also collinear}\blacksquare \end{multline}\)

10/21/2024

$OABC$ and $ODEF$ are squares. $AE \cap BF=G$, $M$ is the midpoint of $CD$. Prove that $GOM$ are collinear.

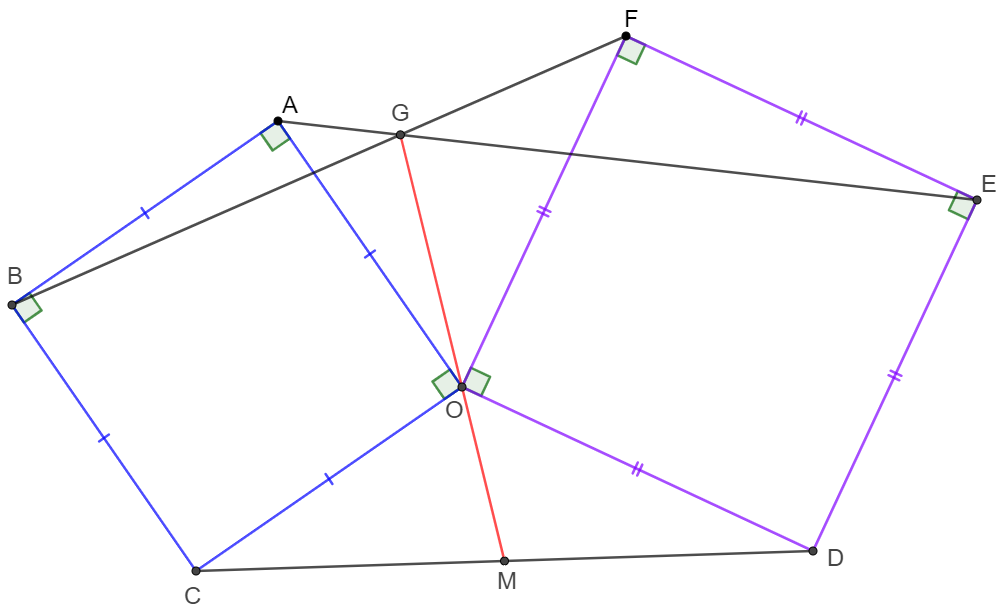
image-20241020193327153

Prove:

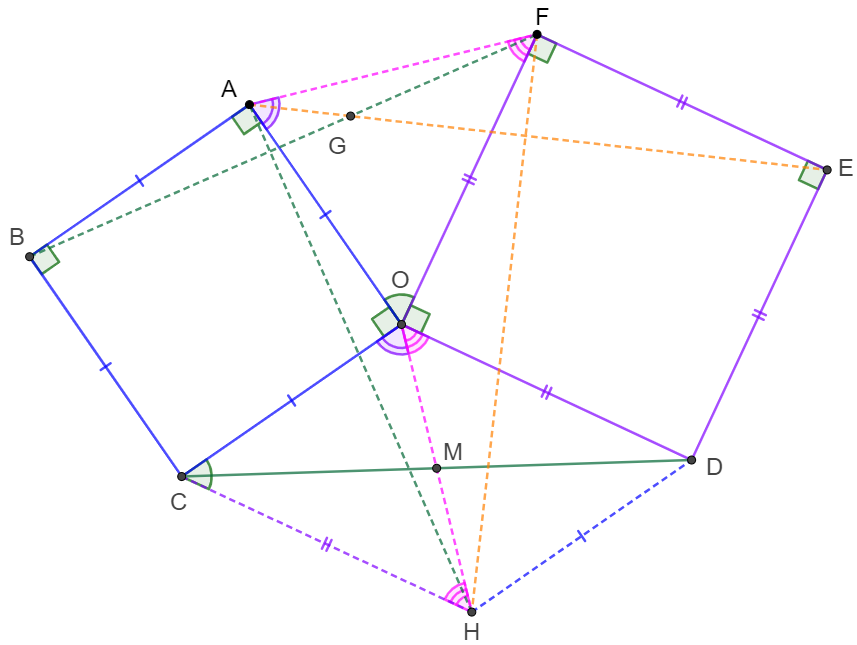image-20241021171957037 \(\begin{multline} \shoveleft CM=MD, \text{Extend }OM \text{ to }H \text{ such that }OM=MH \implies CHDO \text{ is a parallelogram}\\ \shoveleft \implies CH=DO=FO, \angle{CHO}=\angle{DOH}, \angle{HCO}+\angle{COD}=180^{\circ} \implies \angle{HCO}=\angle{AOF}\\ \shoveleft \implies \triangle{AOF} \cong \triangle{OCH}\implies HO=AF, \angle{OAF}=\angle{COH}, \angle{AFO}=\angle{OHC}=\angle{DOH}\\ \shoveleft \implies \angle{BAF}=\angle{AOH}, \angle{AFE}=\angle{HOF}\implies \triangle{BAF}\cong\triangle{AOH},\triangle{AFE}\cong\triangle{HOF}\\ \shoveleft AB\perp AO, EF \perp FO \implies BF\perp AH, AF\perp HO, AE \perp HF\\ \shoveleft \implies G=AE \cap BF \text{ is the orthocenter of }\triangle{AFH}, HO \perp AF \implies GOMH \text{ is collinear}\blacksquare \end{multline}\)

10/26/2024

Bretschneider’s formula in non-trigonometry format: Given the length of sides as $a,b,c,d$, and lengths of diagonals as $m,n$ of quadrilateral $ABCD$. Show that the area $[ABCD]=\dfrac{1}{4}\sqrt{4m^2n^2-(a^2+c^2-b^2-d^2)^2}$

Prove:

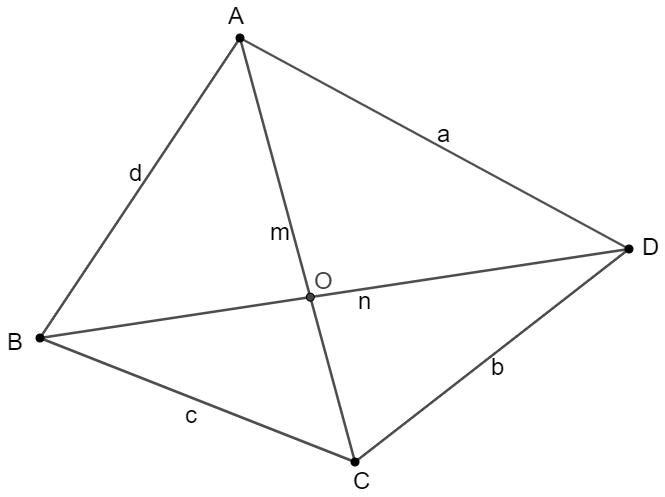image-20241027004625265 \(\begin{multline} \shoveleft \text{Let } S=[ABCD], AC \cap BD = O, \angle{AOB}=\angle{COD}=\phi\\ \shoveleft 2AO\cdot BO \cdot cos\phi=AO^2+BO^2-d^2, 2CO \cdot DO\cdot cos\phi = CO^2+DO^2-b^2\\ \shoveleft 2AO \cdot DO \cdot cos\phi=a^2 - AO^2 - DO^2, 2BO \cdot CO \cdot cos\phi = c^2-BO^2-CO^2, \\ \shoveleft \implies 2mn\cdot cos\phi=a^2+c^2-b^2-d^2 \implies cos\phi=\dfrac{a^2+c^2-b^2-d^2}{2mn}\\ \shoveleft \text{ And since } S=\dfrac{mn\cdot sin\phi}{2} \implies sin\phi=\dfrac{2S}{mn} \implies (\dfrac{2S}{mn})^2+(\dfrac{a^2+c^2-b^2-d^2}{2mn})^2=1\\ \shoveleft \implies S = [ABCD] = \dfrac{1}{4}\sqrt{4m^2n^2-(a^2+c^2-b^2-d^2)^2} \blacksquare \end{multline}\)

Note: This proof comes from A Treatise on Plane Trigonometry, pp. 204–205

    © M∀TH Workout 2020-2021
    Search