M∀TH Workout

September, 2024

 
  • Sep 19, 2024

09/19/2024

$D$ is a point inside $\triangle{ABC}$ such that $\angle{DBC}=\angle{DCB}=9^{\circ}$, $\angle{ABD}=15^{\circ}$, $\angle{BAD}=54^{\circ}$, find $\angle{DAC}$.

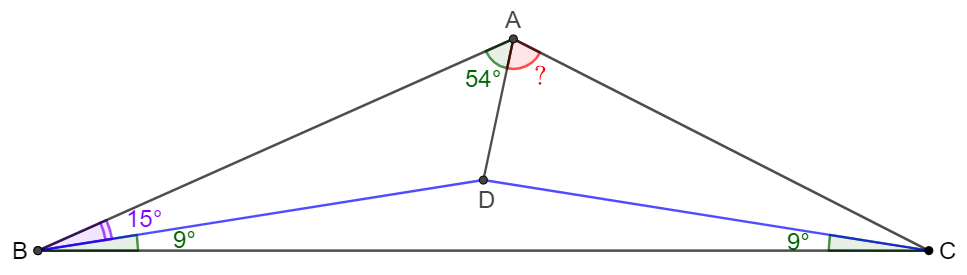
image-20240924034542175

Solve:

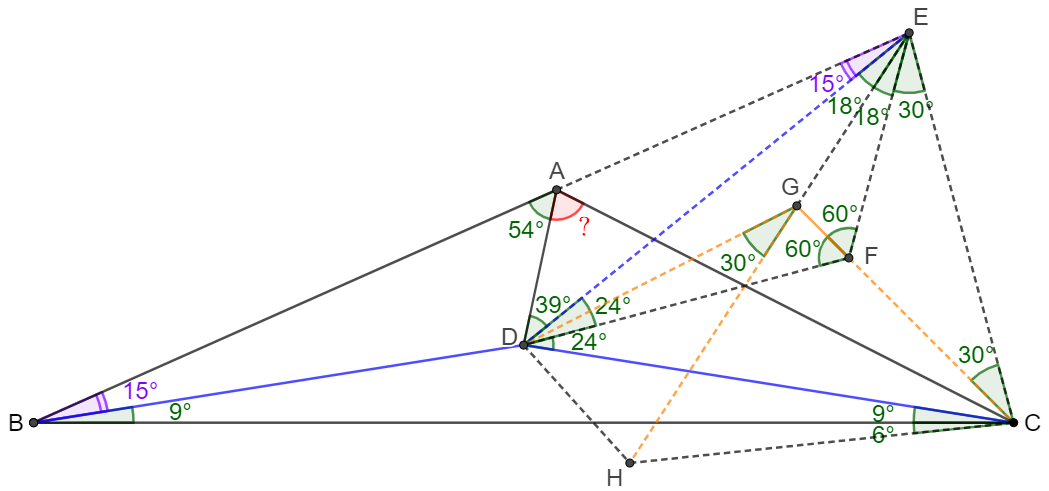image-20240924063356943 \(\begin{multline}\nonumber \shoveleft \text{Extend }BA \text{ to }E \text{ such that }BD=CD=DE \implies \angle{BED}=\angle{ABD}=15^{\circ}\\ \shoveleft \implies \angle{CDE}=2*\angle{ABD}+2*\angle{DBC}=48^{\circ} \implies \angle{DCE}=\angle{DEC}=66^{\circ}\\ \shoveleft \text{Let }F \text{ be a point inside isoseles } \triangle{DCE} \text{ such that }\angle{FEC}=\angle{FCE}=30^{\circ}\\ \shoveleft \implies \angle{DEF}=\angle{DCF}=36^{\circ}, \angle{EDF}=\angle{CDF}=\dfrac{\angle{CDE}}{2}=24^{\circ} \implies \angle{DFE}=120^{\circ}\\ \shoveleft \implies \text{Let }G \text{ be the intersect of the bisector of }\angle{DEF} \text{ and extended }CF\\ \shoveleft \implies \angle{EFG}=60^{\circ} \implies \angle{DFG}=60^{\circ}\implies G \text{ is the incenter of }\triangle{DEF}\\ \shoveleft \implies \angle{EDG}=\angle{GDF}=\dfrac{\angle{CDF}}{2}=12^{\circ}\implies \angle{GDC}=12^{\circ}+24^{\circ}=36^{\circ}=\angle{DCF}\\ \shoveleft \implies DG=CG, \angle{DGC}=180^{\circ}-2*36^{\circ}=108^{\circ}\\ \shoveleft \text{Extend }EG \text{ to }H \text{ such that }DG=CG=GH\implies H \text{ is the circumcenter of }\triangle{CDH}\\ \shoveleft \implies \angle{DGH}=\angle{EDG}+\angle{DEG}=30^{\circ}=2\angle{DCH}, \angle{HGC}=108^{\circ}-30^{\circ}=2\angle{CDH}\\ \shoveleft \implies \angle{DCH}=15^{\circ}=\angle{BED},\angle{CDH}=39^{\circ}=54^{\circ}-15^{\circ}=\angle{ADE}\implies \triangle{ADE}\cong \triangle{HDC}\\ \shoveleft \implies AE=CH, \angle{AEC}=\angle{HCE}\implies \triangle{AEC}\cong\triangle{HCE}\\ \shoveleft \implies \angle{EAC}=\angle{CHE}=180^{\circ}-48^{\circ}-66^{\circ}-15^{\circ}=51^{\circ}\\ \shoveleft \implies \angle{DAC}=180^{\circ}-54^{\circ}-51^{\circ}=\bbox[5px, border: 1px solid black]{75^{\circ}} \end{multline}\)

9/24/2024

$\angle{BAC}=60^{\circ}$ for $\triangle{ABC}$. $H$ is the orthocenter of $\triangle{ABC}$ and $D$ is the midpoint of arc $BC$ on the other side of $A$. Prove that $AH=DH$.

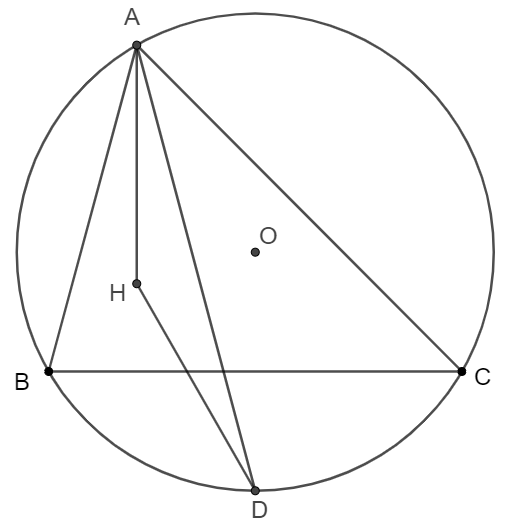
image-20240924115539275

Prove:

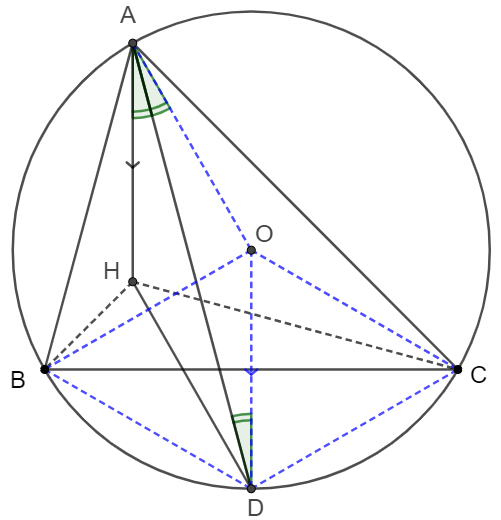image-20240924123221567 \(\begin{multline} \shoveleft \text{Let }H, O \text{ be the orthocenter and circumcenter of }\triangle{ABC}\\ \shoveleft \implies \angle{BAH}=\angle{CAO}, \angle{ABH}=\angle{CBO}, \angle{BCH}=\angle{ACO}\\ \shoveleft \implies \angle{BHC}=\angle{ABH}+\angle{BAC}+\angle{ACH}=\angle{CBO}+\angle{BCO}+\dfrac{\angle{BOC}}{2}\\ \shoveleft =180^{\circ}-\dfrac{\angle{BOC}}{2}=180^{\circ}-\angle{BAC}=180^{\circ} - 60^{\circ}=120^{\circ}=\angle{BOC}\\ \shoveleft \implies BHOC \text{ is cyclic }\\ \shoveleft D \text{ is the midpoint of arc } BC \implies \angle{BOD}=\angle{COD}=\angle{BAC}=60^{\circ}, \angle{BAD}=\angle{CAD} \\ \shoveleft \implies \angle{HAD}=\angle{OAD}=\angle{ODA}, BO=DO=CO=BD=CD\\ \shoveleft \implies AH \parallel OD, D \text{ is the circumcenter of }BHOC \implies DH=DB=OD=AO\\ \shoveleft \implies AODH \text{ is a rhombus} \implies AH=DH \blacksquare \end{multline}\)

09/25/2024

$F$ is a point on side $CD$ of square $ABCD$. Extend $AF$ to $E$ such that $DE \parallel AC$ and $AC=AE$. Prove that $CE=CF$.

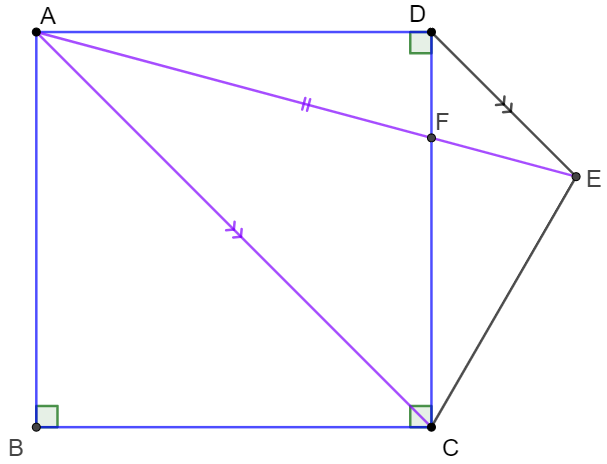
image-20240924200843096

Prove:

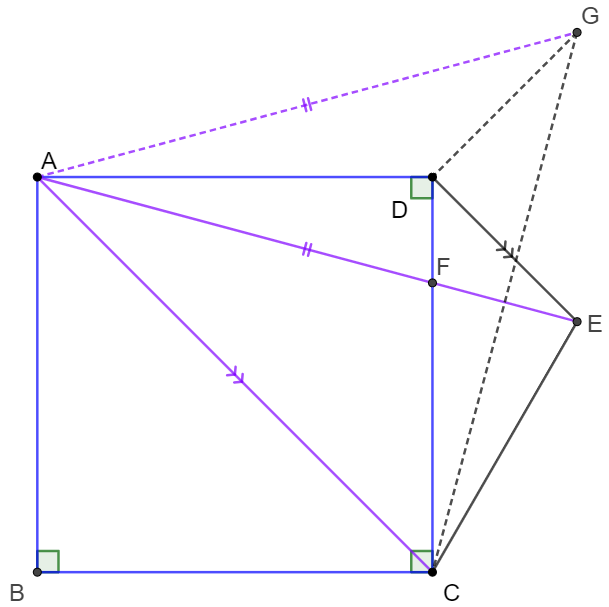image-20240924200747623 \(\begin{multline} \shoveleft DE \parallel AC \implies \angle{CDE}=45^{\circ}\implies \angle{ADE}=135^{\circ}\\ \shoveleft \text{Make }G \text{ the mirror of }E \text{ along } AD \implies \triangle{ADE}\cong\triangle{ADG}\\ \shoveleft \implies AE=AG, \angle{ADG}=\angle{ADE}=135^{\circ}\implies \angle{EDG}=90^{\circ}\\ \shoveleft \implies \angle{CDG}=135^{\circ}=\angle{ADG}\implies \triangle{ADG}\cong\triangle{CDG}\\ \shoveleft \implies AG=CG=AC\implies \triangle{ACG} \text{ is equilateral }\\ \shoveleft \implies \angle{DCG}=\angle{DAG}=60^{\circ}-45^{\circ}=15^{\circ} \implies \angle{CFE}=\angle{AFD}=75^{\circ}\\ \shoveleft \text{ and } \angle{AED}=\angle{AGD}=\angle{CGD}=30^{\circ}=\angle{CAE}\implies \angle{CFE}=75^{\circ}\\ \shoveleft \text{ and } \angle{ACE}=\angle{AEC}=\dfrac{180^{\circ}-30^{\circ}}{2}=75^{\circ}=\angle{CFE}\implies CE=CF\blacksquare\\ \end{multline}\)

09/26/2024

$\angle{BAC}=20^{\circ}, AB=AC$, $D$ is on $AB$ such that $\angle{BDC}=30^{\circ}$, prove that $AD=BC$.

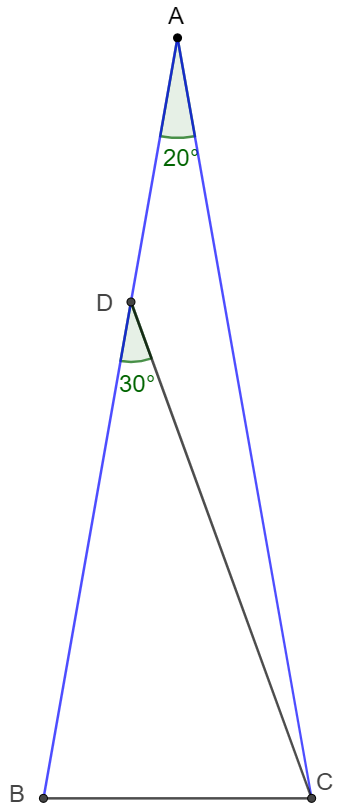
image-20240924205313463

Prove:

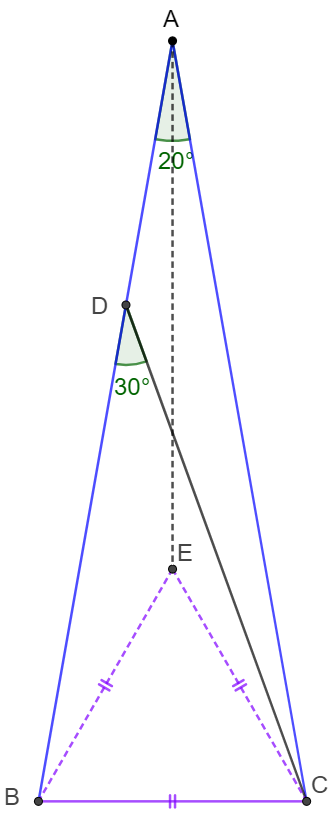image-20240924205739373 \(\begin{multline} \shoveleft \text{Make }\triangle{BCE} \text{ an equilateral triangle inside }\triangle{ABC} \implies \\ \shoveleft \angle{ABE}=80^{\circ}-60^{\circ}=20^{\circ}=\angle{BAC}, \angle{BAE}=\angle{CAE}=10^{\circ}=\angle{ACD}\\ \shoveleft \implies \triangle{BCE}\cong\triangle{ACD}\implies AD=BE=BC\blacksquare \end{multline}\) Note: can also prove it by making equilateral triangle $\triangle{ADE}$ with side $AD$ to the left of $AD$, so $\triangle{ACE}\cong\triangle{ABC}$.

09/27/2024

$\angle{ABC}=3\angle{ACB}$ in $\triangle{ABC}$. $D$ is the midpoint of side $BC$ and $\angle{ADB}=45^{\circ}$. Prove that $\angle{BAC}=90^{\circ}$

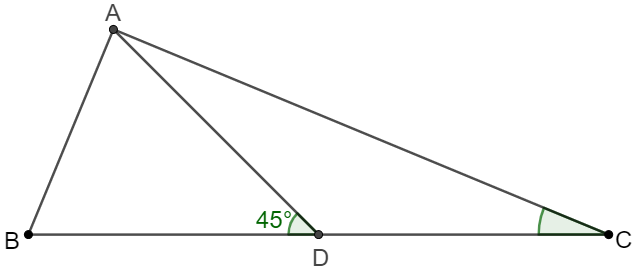
image-20240925020328636

Prove:

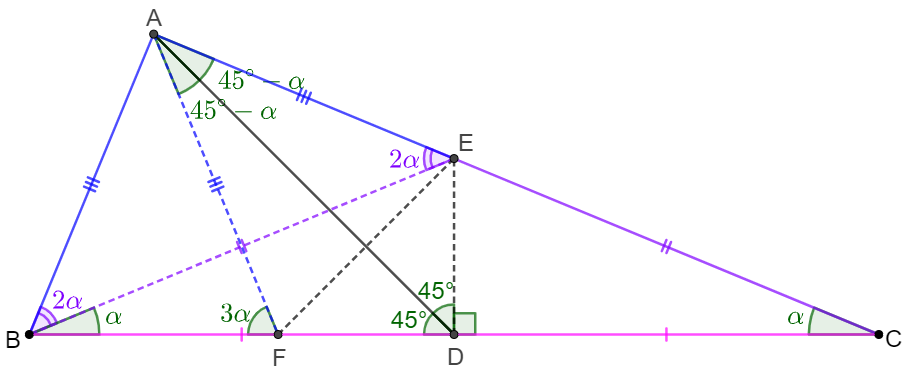image-20240925022518259 \(\begin{multline} \shoveleft \text{Make }E \text{ on }AC \text{ such that }DE \perp BC \implies BE=CE, \angle{EBC}=\angle{ECB}, \angle{ADE}=\angle{ADB}=45^{\circ}\\ \shoveleft \text{Let }\angle{EBC}=\angle{ECB}=\alpha \implies \angle{AEB}=2\alpha=\angle{ABE}\implies AB=AE\\ \shoveleft \text{Make }F \text{ on }BC \text{ such that }DE=DF \implies \triangle{ADF}\cong\triangle{ADE}\implies AF=AE=AB\\ \shoveleft \implies \angle{AFB}=\angle{ABF}=3\alpha \implies \angle{EAF}=2\alpha=2\angle{EAD}=2(\angle{DEC}-45^{\circ})=2(90^{\circ}-\alpha-45^{\circ})\\ \shoveleft =2(45^{\circ}-\alpha)=2\alpha \implies \alpha=22.5^{\circ}\implies ABC=67.5^{\circ}\implies \angle{BAC}=90^{\circ}\blacksquare \end{multline}\) Note: Another observation says $AB=BE, \angle{ADB}=\angle{ADE} \implies BAED \text{ is cyclic}$, but this is not necessary true. When $AD=DE$, the bisector of $\angle{ADE}$ is the same line as perpendicular bisector of $AE$, then any point $B$ on this line satisfies $AB=BE, \angle{ADB}=\angle{ADE}$, but obviously there is only one of them on the circumcircle of $\triangle{ADE}$.

09/28/2024

$\angle{ACB}=30^{\circ}$ for $\triangle{ABC}$, $D$ is the midpoint of side $BC$ and $\angle{ADB}=45^{\circ}$. Find$\angle{BAD}$.

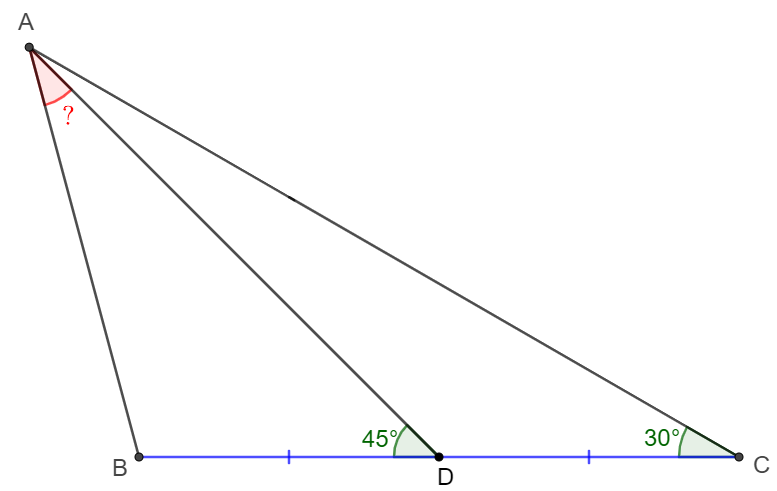
image-20240926121711492

Solve:

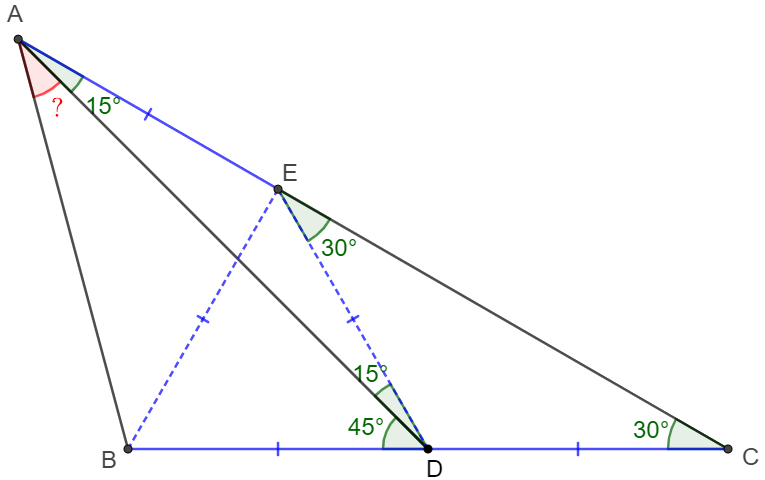image-20240926121841365 \(\begin{multline} \shoveleft \text{Make }E \text{ on }AC \text{ such that }CD=DE \implies \angle{CED}=\angle{DCE}=30^{\circ}\\ \shoveleft \implies \angle{BDE}=60^{\circ},\angle{ADE}=15^{\circ}=\angle{DAE}=45^{\circ}-30^{\circ}\\ \shoveleft \implies QE=DE=CD=BD \implies \triangle{BDE}\text{ is equilateral}\\ \shoveleft \implies \angle{BDE}=60^{\circ},BE=AE \implies \angle{AEB}=90^{\circ}\\ \shoveleft \implies \angle{BAE}=45^{\circ} \implies \angle{BAD}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search