08/01/2024

Two points $P$ and $Q$ are randomly chosen on a circle $C$. What is the probability that the smaller arc between $P$ and $Q$ measures less than $60^\circ$?

Solve 1:

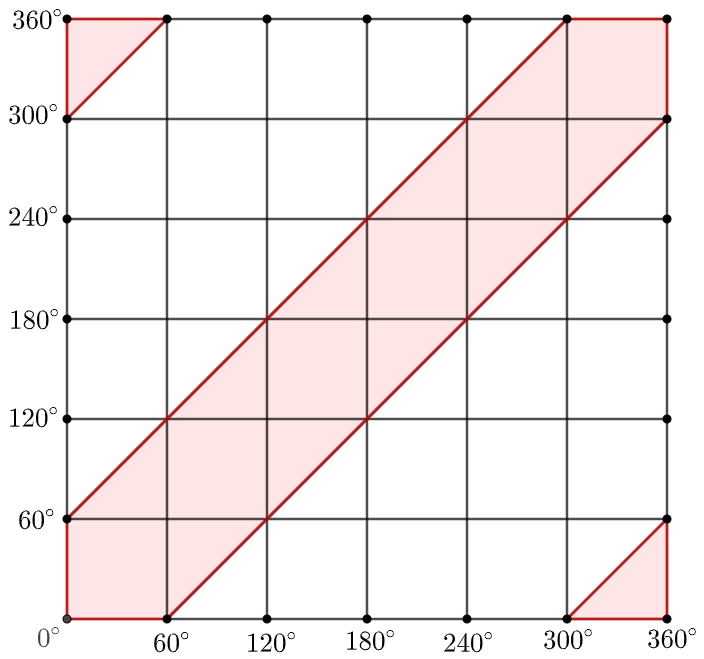
\(\begin{multline} \shoveleft \text{It is natural to think of using coordinates for the successful area between }p=q-60^{\circ} \text{ and } p=q+60^{\circ}\\ \shoveleft \text{But be careful, there are some special corner cases since this is a circle:}\\ \shoveleft \text{When }p=0^{\circ}, q=59^{\circ} \text{ is good}, \text{ but }q=301^{\circ} \text{ is also good, and thus as }p \text{ increases to }60^{\circ}, q \text{ also increases to }359^{\circ}\\ \shoveleft \text{Similarly, when }p=301^{\circ}, q=240^{\circ} \text{ is good, but }q=0^{\circ} \text{ is also good, and thus as }p \text{ increses to }360^{\circ}, q \text{ also increases to }61^{\circ}\\ \shoveleft \text{So the requested probability is } \dfrac{12}{36}=\bbox[5px, border: 1px solid black]{\dfrac{1}{3}}\\ \end{multline}\)

Solve 2: \(\begin{multline} \shoveleft \text{By fix point }P, \text{ then } Q \text{ will fall anywhere within }60^{\circ} \text{ left or right of } P,\\ \shoveleft \text{ which is an arc of }120^{\circ}, \text{ therefore the probability is }\dfrac{120^{\circ}}{360^{\circ}}=\bbox[5px, border: 1px solid black]{\dfrac{1}{3}} \end{multline}\)

---

08/02/2024

$\odot{I}$ is the incircle of $\triangle{ABC}$ and $\odot{E}$ is an inscribed circle tangent with $AC$ and $BC$. $\odot{I} \cap \odot{E}$ at $F, G$. Extended $FG$ and $BI$ intersect at $J$. Extended $FG$ and $AC$ intersect at $H$. Show that $AIHJ$ is cyclic.

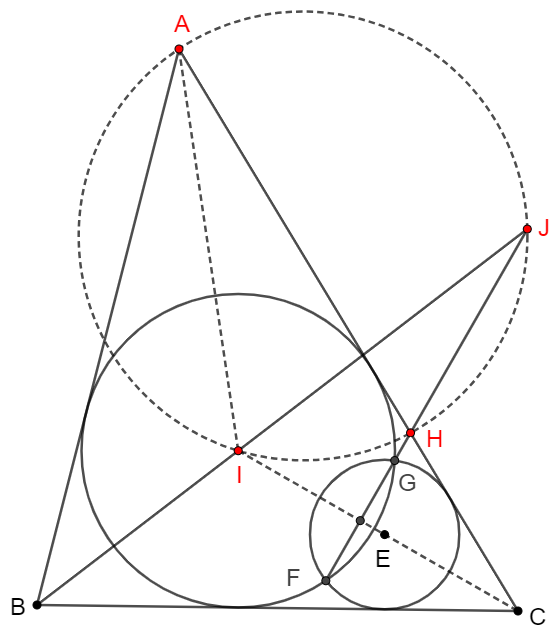
Prove:

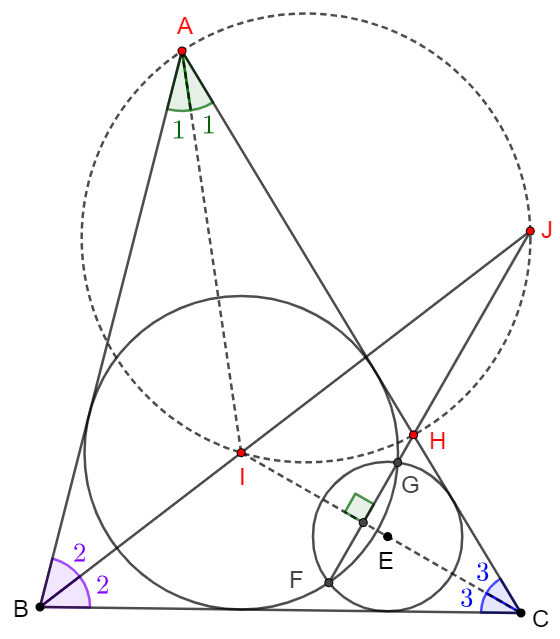\(\begin{multline} \shoveleft \odot{I} \cap \odot{E}=FG \implies IE \perp FG \implies \angle{CIJ}+\angle{IJH}=90^{\circ}\\ \shoveleft \angle{CIJ}=\angle{CBI}+\angle{BCI}=\dfrac{\angle{ABC}+\angle{ACB}}{2}=90^{\circ}-\dfrac{\angle{BAC}}{2}\\ \shoveleft =90^{\circ}-\angle{IAH}\implies \angle{IJH}=\angle{IAH}\implies AIHJ \text{ is cyclic}\blacksquare \end{multline}\)

---