07/02/2014
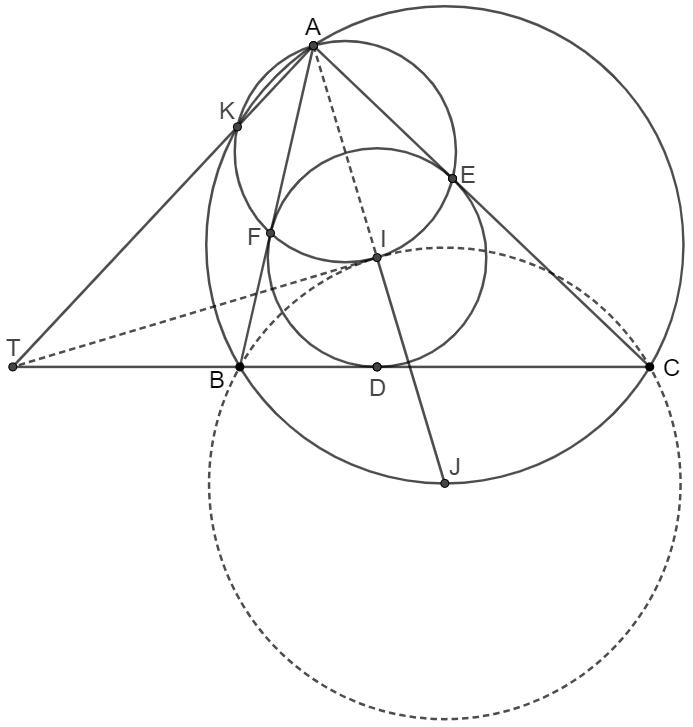
$I$ is the incenter of $\triangle{ABC}$ and $D,E,F$ are the touch points of incircle on side $BC, CA, AB$ respectively. $\odot{AEF} \cap \odot{ABC}=K (K \ne A), AK \cap BC=T$, prove that $AI \perp TI$
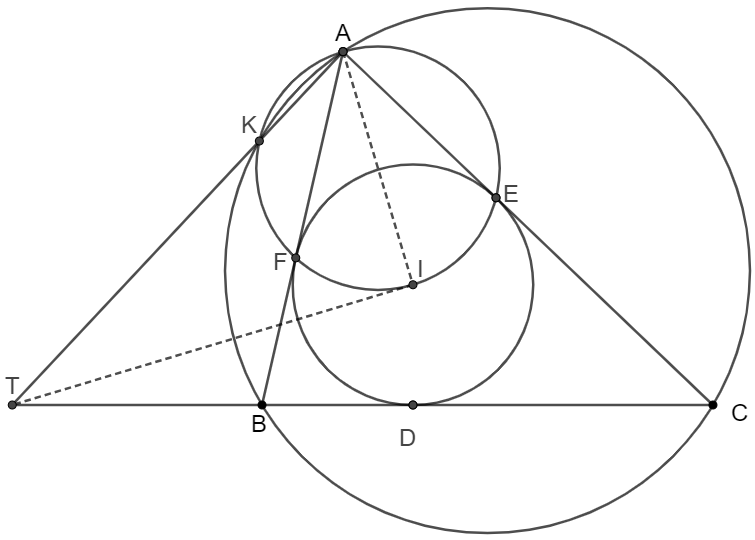
Prove:
\(\begin{multline}
\shoveleft AT \text{ is the radical axis of }\odot{AKFIE} \text{ and } \odot{ABC}\\
\shoveleft BC \text{ is the radical axis of }\odot{BIC} \text{ and } \odot{ABC}\\
\shoveleft \implies T \text{ is the radical center of three circles }\\
\shoveleft \text{By properties of incenter configuration, the center of }\odot{BIC}\\
\shoveleft \text{is the midpoint of arc }\overset{\huge\frown}{BC} \text{ of } \odot{ABC} \text{ which does not contain }A\\
\shoveleft \implies I=\odot{AKFIE} \cap \odot{BIC} \implies TI \perp AI \blacksquare
\end{multline}\)
Note:
- $K$ is called Shaky-Devil point on Lemmas in Olympiad Geometry from Evan Chen’s EGMO page, and there is an AOPS community blog about its properties.
- There is a six-part detailed introduction to Incenter-Related Configurations on an AOPS community blog but in bad format. I am going to make a clean format of it.
07/13/2024
Richard and Vanessa are going to play a game of foosball. The first player to score 5 goals wins. Vanessa is better: at any given point she is $60\%$ likely to score the next goal. What is the probability that Richard wins?
Solve: \(\begin{multline} \shoveleft \text{Richard will win when he has got 4 goals and will score the next goal.}\\ \shoveleft \text{Consider how many goals has Vanessa got now, here is the case work:}\\ \shoveleft \begin{cases} \text{case 1: Vanessa goals = 0, Richard goals = 4: } \displaystyle {4 \choose 0} \times0.6^0 \times 0.4^4 \times 0.4\\ \text{case 2: Vanessa goals = 1, Richard goals = 4: } \displaystyle {5 \choose 1} \times 0.6^1\times 0.4^4 \times 0.4\\ \text{case 3: Vanessa goals = 2, Richard goals = 4: } \displaystyle {6 \choose 2} \times 0.6^2 \times 0.4^4 \times 0.4\\ \text{case 4: Vanessa goals = 3, Richard goals = 4: } \displaystyle {7 \choose 3} \times 0.6^3 \times 0.4^4 \times 0.4\\ \text{case 5: Vanessa goals = 4, Richard goals = 4: } \displaystyle {8 \choose 4} \times 0.6^4 \times 0.4^4 \times 0.4\\ \end{cases}\\ \shoveleft \implies \sum(cases)=0.26656768 \approx \bbox[5px, border: 1px solid black]{26.66\%} \end{multline}\\\)
07/14/2024
In the card game bridge, each of 4 players is dealt a hand of 13 of the 52 cards. What is the probability that each player receives exactly one Ace?
Solve 1: \(\begin{multline} \shoveleft \text{Suppose the }52 \text{ cards have been numbered such that 1-13, 14-26, 27-39, 40-52 cards}\\ \shoveleft \text{will be in the hand of the first, second, third and fourth player respectively}\\ \shoveleft \text{but the order of cards in the hand of each player does not matter.}\\ \shoveleft \text{Without losing of generality, we suppose the first Ace has been assigned to the first player}\\ \shoveleft \text{and be numbered as 1st card. Now consider the second Ace card: }\\ \shoveleft \text{It could be numbered from 2-52, and if it is numbered from 14-52,}\\ \shoveleft \text{ it is not in the hand of the first player. So it has probability of }\dfrac{52-13}{52-1}\\ \shoveleft \text{ to be not in the hand of the same player.}\\ \shoveleft \text{Then consider the third Ace card, it could be numbered from 3-52, and there are 26 numbers}\\ \shoveleft \text{ will guarantee it is not in the hand of any player who already owns an Ace card, which means }\\ \shoveleft \text{ the probability is }\dfrac{52-26}{52-2}. \text{ Similarly, the probability of the fourth Ace card is not in the hand}\\ \shoveleft \text{ of any player who already owns an Ace card is }\dfrac{52-39}{52-3}. \text{So the total probability is}\\ \shoveleft \dfrac{39}{51}\times\dfrac{26}{50}\times\dfrac{13}{49}=\dfrac{13^3}{17*35^2}=\dfrac{2197}{20825} \approx \bbox[5px, border: 1px solid black]{0.1055}\\ \end{multline}\) Solve 2: \(\begin{multline} \shoveleft \text{Suppose the }52 \text{ cards have been numbered such that 1-13, 14-26, 27-39, 40-52 cards}\\ \shoveleft \text{will be in the hand of the first, second, third and fourth player respectively.}\\ \shoveleft \text{And we suppose that the order of cards in the hand of each player matters.}\\ \shoveleft \text{This will make the counting easier: the total ways to arrange the 52 cards is }52!\\ \shoveleft \text{There are }4! \text{ ways to assign 4 Ace cards to each player}\\ \shoveleft \text{And for each Ace card, it can be placed as any of the 13 cards that player owns;}\\ \shoveleft \text{this means }13^4 \text{ ways to place the 4 Ace cards to the list to each player.}\\ \shoveleft \text{Then there are }48!\text{ ways to arrange the rest }48 \text{ cards to the list}\\ \shoveleft \text{So the total probability is }\dfrac{4! \times 13^4 \times 48!}{52!}=\dfrac{13^3}{17*35^2}=\dfrac{2197}{20825} \approx \bbox[5px, border: 1px solid black]{0.1055}\approx 10.55\% \end{multline}\) Solve 3: \(\begin{multline} \shoveleft \text{From this }\href{https://www.youtube.com/watch?v=IC-pnm6PEGk}{\text{MIT OpenCourseWare Video}}:\\ \shoveleft \text{The probability is: } \dfrac{4! \displaystyle{48 \choose {12, 12, 12, 12}}}{\displaystyle{52 \choose {13, 13, 13, 13}}}=\dfrac{4!\dfrac{48!}{12! \times 12! \times 12! \times 12!}}{\dfrac{52!}{13! \times 13! \times 13! \times 13!}}=\dfrac{4! \times (13!)^4 \times 48!}{52!}\\ \end{multline}\) Note:
-
The probability that 4 Ace cards are in the same player (4-0-0-0):
$\dfrac{\displaystyle{4 \choose 1} \times P^{13}_{4}\times 48!}{52!}=\dfrac{44}{4165}=\dfrac{220}{20825} \approx 0.01056 \approx 1.06\%$
$20825-2197-220=18408$
Note: $\dfrac{12}{51} \times \dfrac{11}{50} \times \dfrac{10}{49}$ is also correct, but hard to get results in following cases.
-
The probability that 2 out of 4 players get 2 Ace cards each (2-2-0-0):
$\dfrac{\displaystyle{4 \choose 2} \times 4! {13 \choose 2}^2 \times 48!}{52!}=\dfrac{2808}{20825} \approx 0.1348 \approx 13.48\%$
$18408-2808=15600$
-
The probability that 1 player gets 2 Ace cards, another 2 players get 1 Ace card each (2-1-1-0):
$\dfrac{\displaystyle {4 \choose 3} \times {3 \choose 1} \times 4! \times 13^2 \times {13 \choose 2}\times 48!}{52!}=\dfrac{12168}{20825}\approx 0.5843 \approx 58.43\%$
$15600-12168=3432$
-
The probability that one player gets 3 Ace cards, another 1 player gets the rest 1 Ace card (3-1-0-0): $\dfrac{P^4_2 \times 4! \times 13 \times \displaystyle{13 \choose 3 } \times 48!}{52!}=\dfrac{3432}{20825} \approx 0.1648 \approx 16.48\%$
07/29/2024
$D$ is the midpoint of side $AB$ of right angle triangle $\triangle{ABC}$ and $E$ is on hypotenuse $AC$ such that $CE=AD$. $F$ is the midpoint of $DE$, show that $\angle{AED}=\angle{BCF}$.
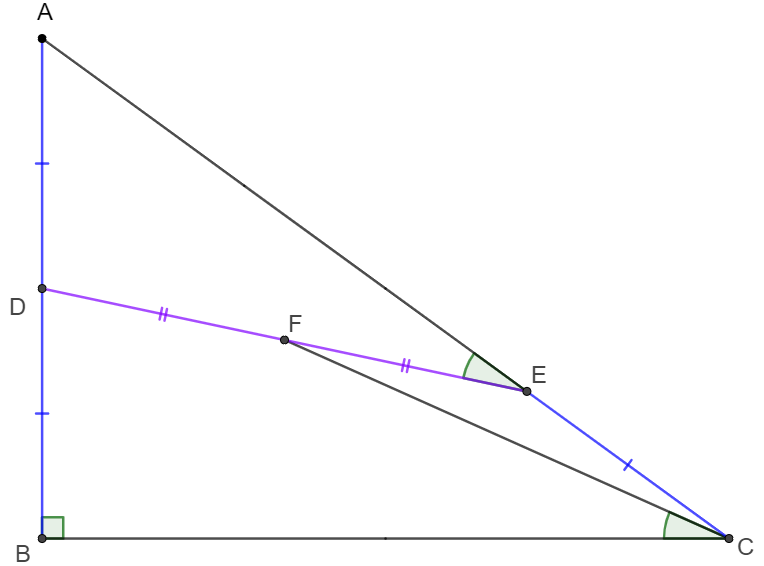
Prove 1:
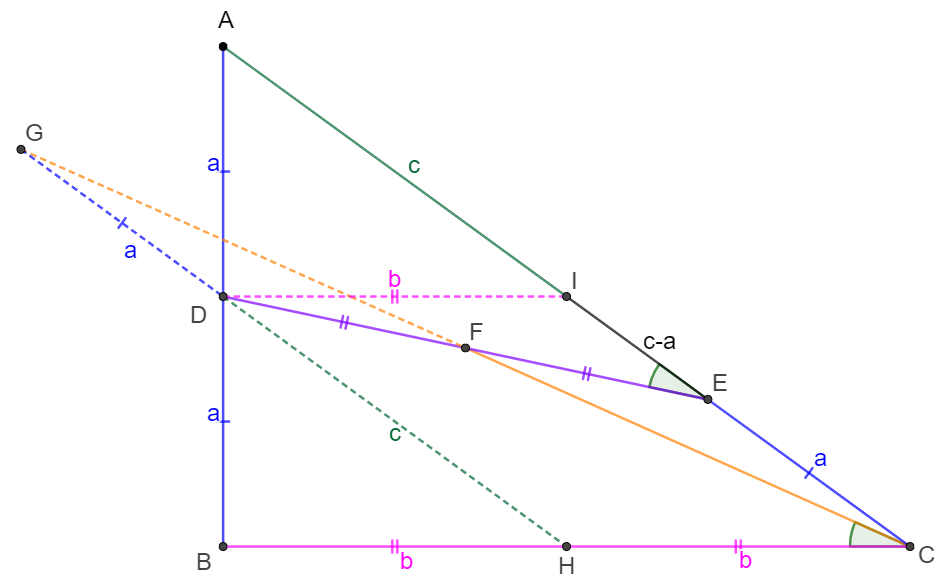\(\begin{multline}
\shoveleft \text{Let } AD=DB=CE=a, AI=IC=c, DI=b \implies DI\parallel BC, BC=2b, EI=IC-CE=c-a\\
\shoveleft \text{Extend } CF \text{ to }G \text{ such that }CF=FG, \text{extend }GD \text{ and }GD \cap BC=H\\
\shoveleft DF=EF \implies \triangle{CEF}\cong\triangle{GDF}\implies CE=GD=a, \angle{ECF}=\angle{DGF}\\
\shoveleft \implies GD\parallel CE \implies DICH \text{ is parallelogram}\implies \triangle{ADI}\cong\triangle{DBH}, \angle{DIE}=\angle{GHC}\\
\shoveleft \implies BH=HC=DI=b, DH=AI=IC=c \implies b^2=c^2-a^2=(c+a)(c-a)\\
\shoveleft \implies DI \cdot HC=GH \cdot EI \implies \triangle{DEI}\sim\triangle{GCH}\implies \angle{AED}=\angle{BCF}\blacksquare
\end{multline}\)
Prove 2:
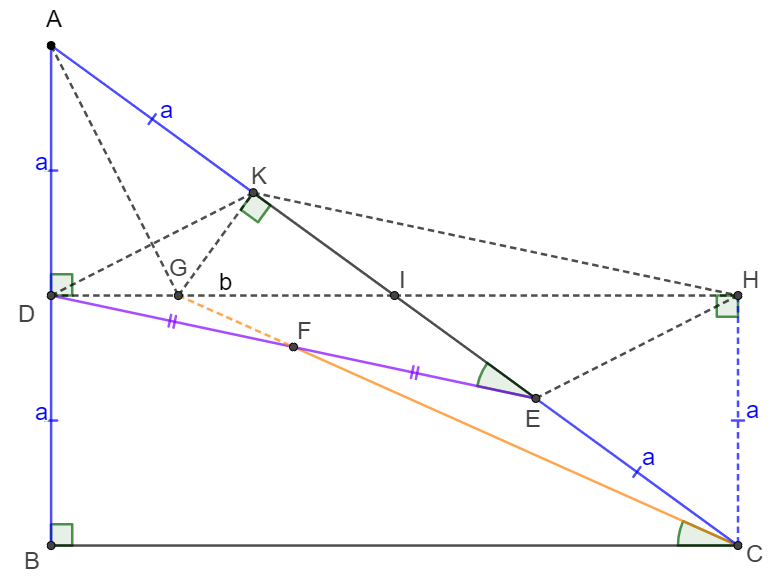\(\begin{multline}
\shoveleft \text{Let }I \text{ be the midpoint of }AC, \text{ extend }CF \text{ such that }CF \cap DI=G\\
\shoveleft \text{Let }AD=DB=CE=a, DI=b, AI=IC=c\\
\shoveleft \text{Apply Menelaus' Theorem to }\triangle{DEI} \text{ and line }CG \implies\\
\shoveleft \dfrac{EF}{FD}\dfrac{DG}{GI}\dfrac{CI}{CE}=1 \implies \dfrac{DG}{GI}=\dfrac{CE}{CI}=\dfrac{a}{c}=\dfrac{AD}{AI}\\
\shoveleft \implies AG \text{ bisects }\angle{DAC}\implies \text{Make }K \text{ on }AC \text{ such that }AK=AD\\
\shoveleft \implies \triangle{DAG}\cong\triangle{KAG}\implies GK\perp AC\implies\\
\shoveleft \text{ Let }CH \perp BC \text{ and } H \text{ on extended }DI \implies \triangle{DHK}\cong\triangle{HDE}\\
\shoveleft \implies DKHE \text{ is parallelogram}, GKHC \text{ is cyclic}\\
\shoveleft \implies \angle{CKH}=\angle{CGH}=\angle{AED}=\angle{BCF} \implies \angle{AED}=\angle{BCF}\blacksquare
\end{multline}\)
Prove 3:
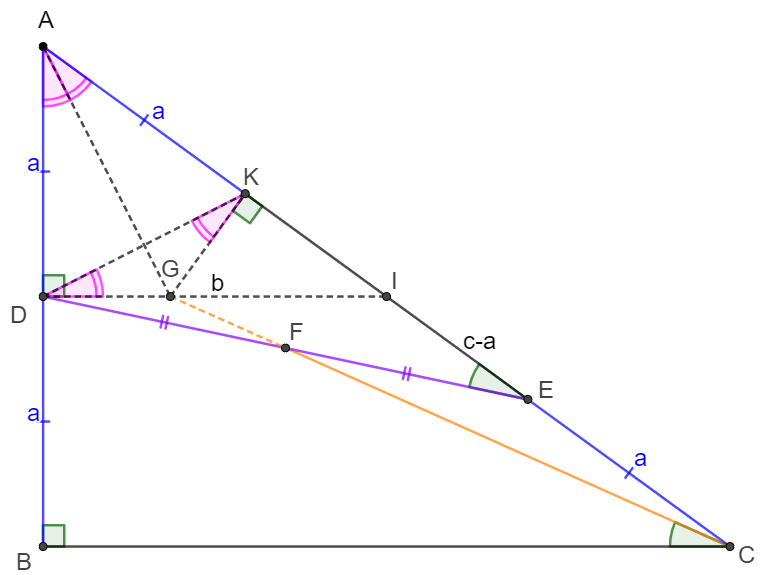\(\begin{multline}
\shoveleft \text{Let }I \text{ be the midpoint of }AC, \text{ extend }CF \text{ such that }CF \cap DI=G \\
\shoveleft \implies DI\parallel BC \implies \angle{AID}=\angle{ACB}\\
\shoveleft \text{ Let }AD=DB=CE=a, DI=b, AI=IC=c\\
\shoveleft \implies a^2+b^2=c^2 \implies b^2=(c+a)(c-a)\implies \dfrac{c-a}{b}=\dfrac{b}{c+a}\\
\shoveleft \text{Apply Menelaus' Theorem to }\triangle{DEI} \text{ and line }CG \implies\\
\shoveleft \dfrac{EF}{FD}\dfrac{DG}{GI}\dfrac{CI}{CE}=1 \implies \dfrac{DG}{GI}=\dfrac{CE}{CI}=\dfrac{a}{c}\implies GI=\dfrac{c}{a+c}b\\
\shoveleft \implies \dfrac{EI}{DI}=\dfrac{c-a}{b}=\dfrac{b}{c+a}=\dfrac{\dfrac{c}{c+a}b}{c}=\dfrac{GI}{CI} \implies \triangle{DEI}\sim \triangle{CGI}\\
\shoveleft \implies \angle{EDI}=\angle{GCI}\implies \angle{AID}-\angle{EDI}=\angle{ACB}-\angle{GCI}\\
\shoveleft \implies \angle{AED}=\angle{BCF}\blacksquare
\end{multline}\)
07/30/2024
$ABCD$ is a cyclic quadrilateral. $\odot{O_1}, \odot{O_2}$ are incircles of $\triangle{ABC}, \triangle{BCD}$ respectively. $EF$ is the other direct common tangents of $\odot{O_1}, \odot{O_2}$ which is not $BC$. Prove that $EF \parallel AD$.
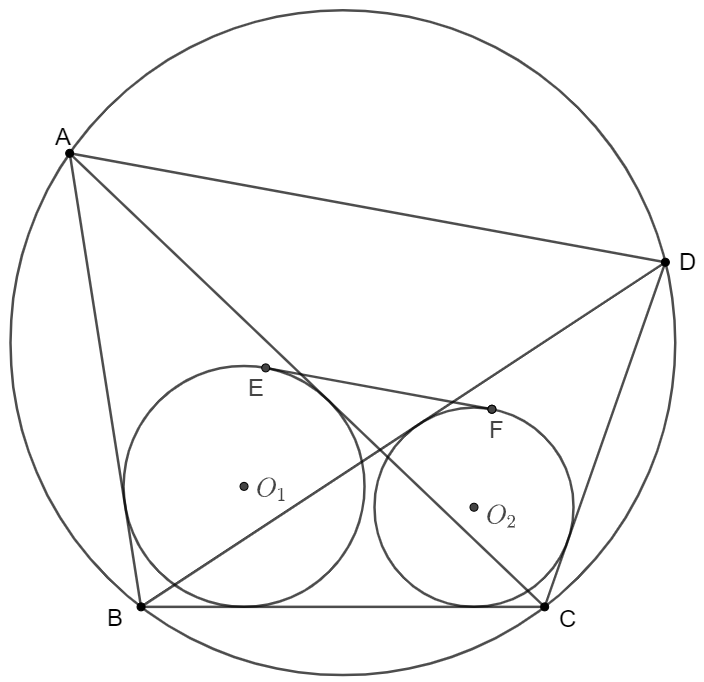
Prove:
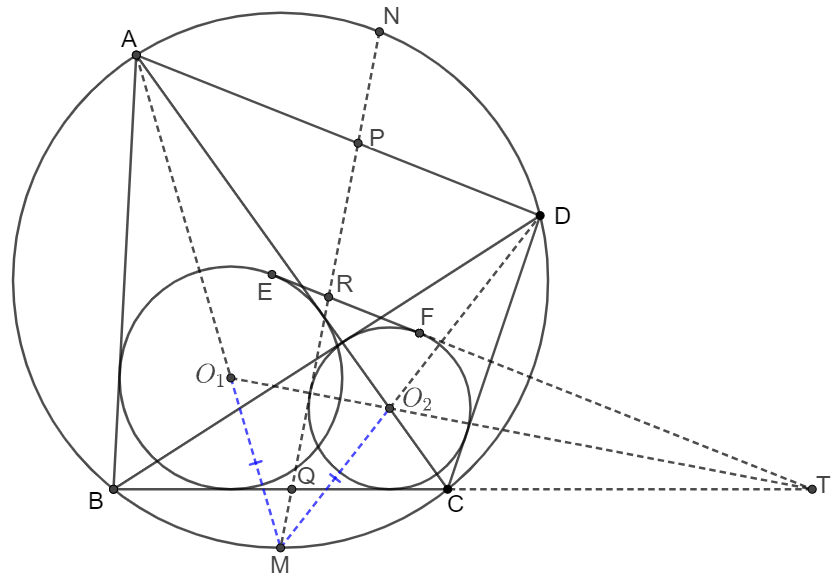\(\begin{multline}
\shoveleft \text{ Since } AO_1, DO_2\text{ bisects }\angle{BAC}, \angle{BDC} \text{ respectively and } \angle{BAC}=\angle{BDC}\\
\shoveleft \implies \text{Extended }AO_1 \text{ and }DO_2 \text{ intersects on the circumcircle of }ABCD\\
\shoveleft \text{Let }M \text{ be the midpoint of }\overset{\huge \frown} {BC} \implies AO_1 \cap DO_2 = M\\
\shoveleft \text{Let } MN \cap AD=P, MN \cap BC=Q, MN \cap EF=R\\
\shoveleft \text{Incenter/Excenter Lemma }\implies BM=MO_1=MC=MO_2\\
\shoveleft \text{Let }N \text{ be the midpoint of }\overset{\huge \frown} {AD} \implies \angle{AMN}=\angle{DMN}\implies O_1O_2 \perp MN\\
\shoveleft \text{Extend }BC, EF \text{ such that }BC \cap EF=T \implies \text{extended }O_1O_2 \cap EF = T\\
\shoveleft \implies \angle{(BC, MN)}=\angle{TQR}=\angle{TRQ}=\angle{(MN, EF)}\\
\shoveleft \angle{(BC,MN)}=\angle{BQM}=\angle{NBC}+\angle{BNQ}=\dfrac{\angle{ABD}}{2}+\angle{DBC}+\dfrac{\angle{BNC}}{2}\\
\shoveleft \angle{(MN, AD)}=\angle{APN}=\angle{AMN}+\angle{MAD}=\dfrac{\angle{AMD}}{2}+\dfrac{\angle{BAC}}{2}+\angle{CAD}\\
\shoveleft =\dfrac{\angle{ABD}}{2}+\dfrac{\angle{BNC}}{2}+\angle{DBC}\implies \angle{(BC,MN)}=\angle{(MN, AD)}\\
\shoveleft \implies \angle{(MN, EF)}=\angle{(MN, AD)} \implies EF \parallel AD\blacksquare
\end{multline}\)
Note:
This approach is given at here.
07/31/2024
Japanese theorem for cyclic quadrilaterals - $ABCD$ is a cyclic quadrilateral and $I_{ABC}, I_{ACD}, I_{BCD},I_{ABD}$ are incenters of $\triangle{ABC}, \triangle{ACD}, \triangle{BCD}, \triangle{ABD}$ respectively. Prove that $I_{ABC}I_{BCD}I_{ACD}I_{ABD}$ form a rectangle.
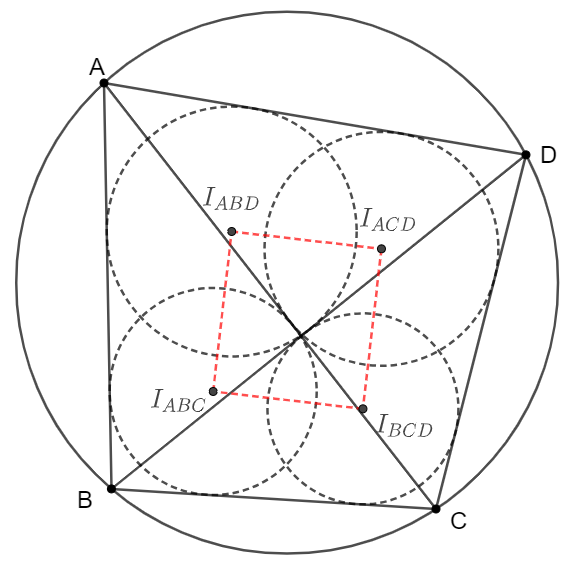
Prove: \(\begin{multline} \shoveleft \angle{AI_{ABD}D}=90^{\circ}+\dfrac{\angle{ABD}}{2},\angle{AI_{ACD}D}=90^{\circ}+\dfrac{\angle{ACD}}{2}, \angle{ABD}=\angle{ACD}\\ \shoveleft \implies \angle{AI_{ABD}D}=\angle{AI_{ACD}D}\implies AI_{ABD}I_{ACD}D \text{ is cyclic } \\ \shoveleft \implies \angle{I_{ABD}AD}+\angle{I_{ABD}I_{ACD}D}=180^{\circ} \implies \dfrac{\angle{BAD}}{2}+\angle{I_{ABD}I_{ACD}D}=180^{\circ}\\ \shoveleft \text{Similarly }CI_{BCD}I_{ACD}D \text{ is cyclic }\implies \angle{I_{BCD}CD}+\angle{I_{BCD}I_{ACD}D}=180^{\circ}\\ \shoveleft \implies \dfrac{\angle{BCD}}{2}+\angle{I_{BCD}I_{ACD}D}=180^{\circ} \text{ and } \angle{BAD}+\angle{BCD}=180^{\circ}\\ \shoveleft \implies \dfrac{\angle{BAD}+\angle{BCD}}{2}+\angle{I_{ABD}I_{ACD}D}+\angle{I_{BCD}I_{ACD}D}=360^{\circ}\\ \shoveleft \implies \angle{I_{ABD}I_{ACD}D}+\angle{I_{BCD}I_{ACD}D}=360^{\circ}-90^{\circ}=270^{\circ}\\ \shoveleft \implies \angle{I_{ABD}I_{ACD}I_{BCD}}=360^{\circ}-270^{\circ}=90^{\circ} \text{ Similarly so are the other three angles}\blacksquare\\ \end{multline}\)