M∀TH Workout

June 2024

 
  • Jun 14, 2024

06/14/2024

$\angle{A}=60^{\circ}$ in $\triangle{ABC}$ and $D$ is the Fermat Point of $\triangle{ABC}$, i.e., $\angle{AEB}=\angle{AEC}=120^{\circ}$. $AD \perp BC$ at $D$. Prove that $AE=2DE$.

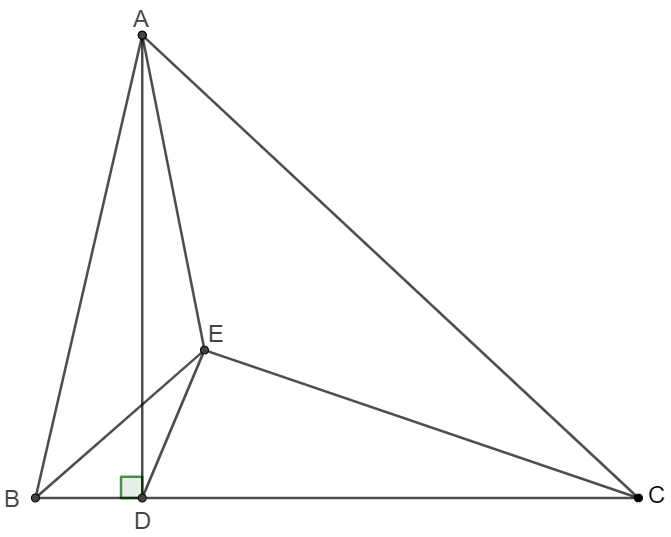
image-20240614143804429

Prove:

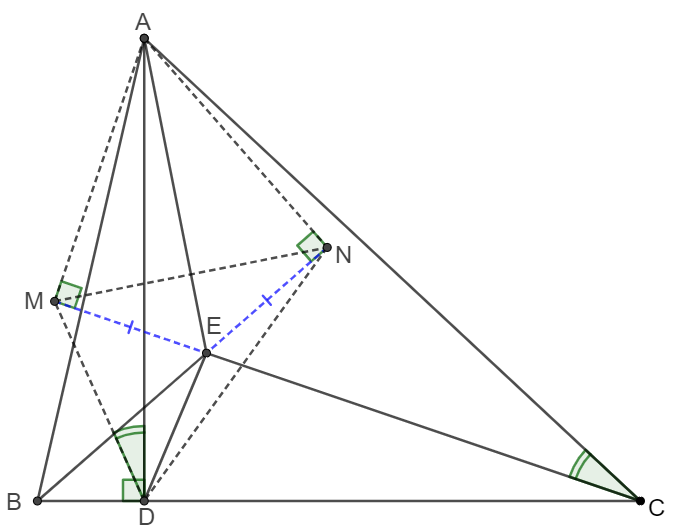image-20240614141120375 \(\begin{multline} \shoveleft \text{Extend } BE \text{ and }CE \text{ to }M,N \text{ respectively such that }AM \perp CM, BN \perp AN\\ \shoveleft \angle{AEB}=\angle{AEC}=120^{\circ}\implies \angle{AEM}=\angle{AEN}=60^{\circ}\\ \shoveleft \implies ME=NE=\dfrac{AE}{2}, \angle{MAN}=60^{\circ}, \angle{MEN}=120^{\circ} \implies \angle{MAB}=\angle{CAN}\\ \shoveleft AN \perp BN, AD \perp BC, AM \perp CM \implies AMDC \text{ is cyclic}, ANDB \text{ is cyclic}\\ \shoveleft \angle{ADN}=\angle{ABN}=90^{\circ}-\angle{BAN}=90^{\circ}-(60^{\circ}-\angle{CAN})=30^{\circ}+\angle{CAN}\\ \shoveleft \angle{ADM}=\angle{ACM}=90^{\circ}-\angle{CAM}=90^{\circ}-(60^{\circ}+\angle{MAB})=30^{\circ}-\angle{MAB}\\ \shoveleft \implies \angle{ADN}+\angle{ADM}=\angle{MDN}=60^{\circ}=\dfrac{\angle{MEN}}{2}\implies\\ \shoveleft E\text{ is the circumcenter of }\triangle{MDN} \implies ME=NE=DE=\dfrac{AE}{2} \blacksquare \end{multline}\)

06/16/2024

$M$ is the midpoint of side $BC$ of $\triangle{ABC}$, $D$ is also on side $BC$ such that $\angle{BAD}=\angle{CAM}$, prove that $\dfrac{BD}{CD}=\dfrac{AB^2}{AC^2}$

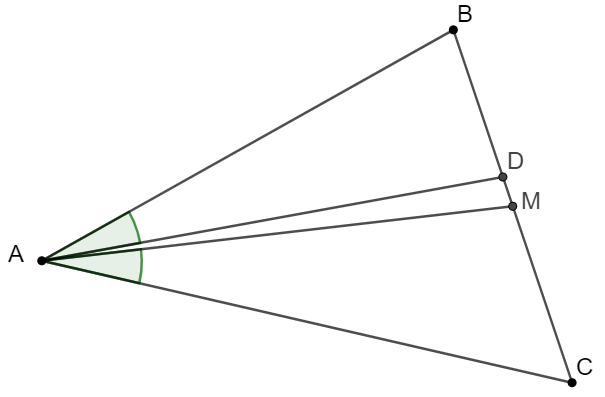
image-20240617041749349

Prove: \(\begin{multline} \shoveleft CM=BM \implies [CAM]=[BAM]\\ \shoveleft \implies \dfrac{1}{2}AC\cdot AM \cdot sin\angle{CAM}=\dfrac{1}{2}AM \cdot AB \cdot sin\angle{BAM} \\ \shoveleft \implies AC \cdot sin\angle{BAD}=AB \cdot sin\angle{CAD}\\ \shoveleft \implies \dfrac{sin \angle{BAD}}{sin \angle{CAD}}=\dfrac{AB}{AC}\implies \dfrac{BD}{CD}=\dfrac{[BAD]}{[CAD]}\\ \shoveleft =\dfrac{\dfrac{1}{2}AB\cdot AD \cdot sin\angle{BAD}}{\dfrac{1}{2}AC\cdot AD \cdot sin\angle{CAD}}=\dfrac{AB \cdot sin\angle{BAD}}{AC \cdot sin\angle{CAD}}=\dfrac{AB^2}{AC^2} \blacksquare\\ \shoveleft \end{multline}\)

06/17/2024

The incircle of $\triangle{ABC}$ touches its sides $BC, CA, AB$ at points $D,E,F$ respectively. The excircles of $\triangle{ABC}$ touch the corresponding sides of $\triangle{ABC}$ at points $T, U, V$ (these points are inside the segments $BC, CA, AB$). Show that $[DEF]=[TUV]$.

Prove:

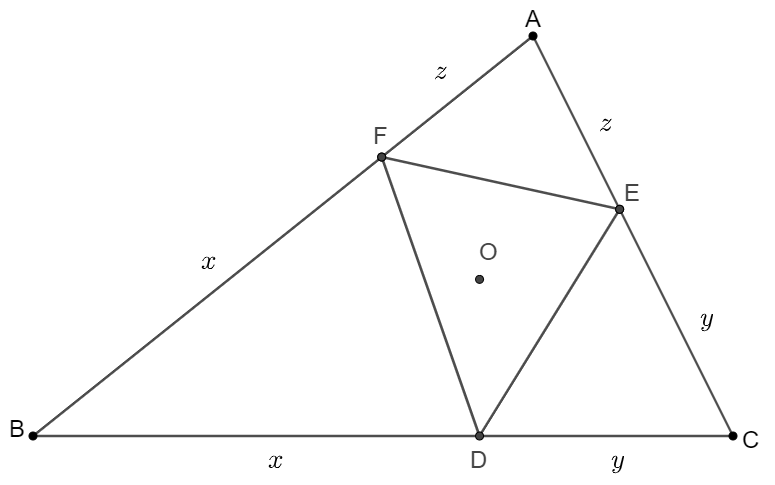image-20240617033608015 \(\begin{multline} \shoveleft \text{Get the barymetric coordinates of }D,E,F:\\ \shoveleft \text{Let }BD=BF=x, CD=CE=y, AE=AF=z\\ \shoveleft \implies x+y=a,y+z=b,z+x=c\\ \shoveleft \implies x=\dfrac{a-b+c}{2},y=\dfrac{a+b-c}{2},z=\dfrac{-a+b+c}{2}\implies \\ \shoveleft D(0, \dfrac{a-b+c}{2},\dfrac{a+b-c}{2})\\ \shoveleft E(\dfrac{-a+b+c}{2}, 0, \dfrac{a+b-c}{2})\\ \shoveleft F(\dfrac{-a+b+c}{2}, \dfrac{a-b+c}{2},0)\\ \shoveleft [DEF]=[ABC]\cdot \begin{vmatrix} 0 & \dfrac{a-b+c}{2} & \dfrac{a+b-c}{2}\\ \dfrac{-a+b+c}{2} & 0 & \dfrac{a+b-c}{2}\\ \dfrac{-a+b+c}{2} & \dfrac{a-b+c}{2} & 0 \end{vmatrix}\\ \shoveleft =[ABC]\cdot \dfrac{(-a+b+c)(a-b+c)(a+b-c)}{4} \end{multline}\) 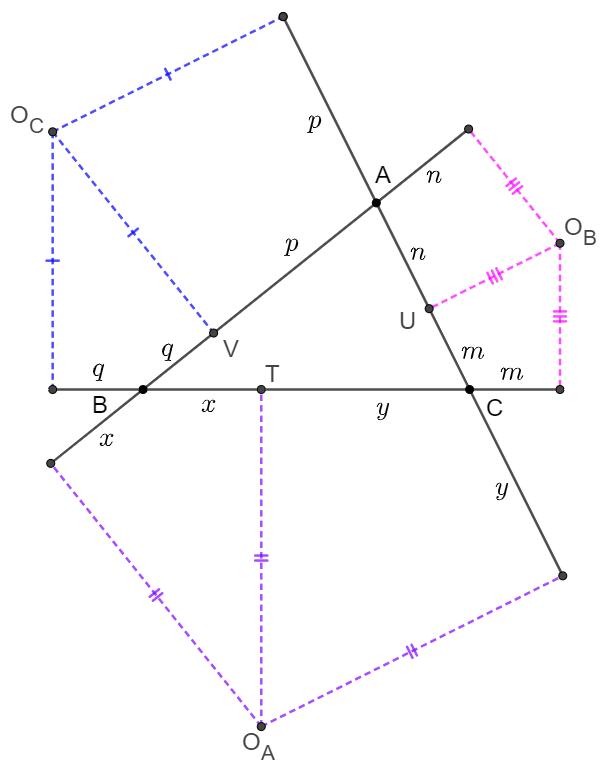image-20240617035646409 \(\begin{multline} \shoveleft \text{Similarly, get the barycentric coordinates of }T,U,V:\\ \shoveleft x+y=a,x+c=y+b\implies x=\dfrac{a+b-c}{2},y=\dfrac{a-b+c}{2}\\ \shoveleft \implies T(0, \dfrac{a+b-c}{2}, \dfrac{a-b+c}{2})\\ \shoveleft m+n=b, m+a=n+c\implies m=\dfrac{-a+b+x}{2}, n=\dfrac{a+b-c}{2}\\ \shoveleft \implies U(\dfrac{a+b-c}{2}, 0, \dfrac{-a+b+c}{2})\\ \shoveleft p+q=c, p+b=q+a\implies p=\dfrac{a-b+c}{2},q=\dfrac{-a+b+c}{2}\\ \shoveleft \implies V(\dfrac{a-b+c}{2}, \dfrac{-a+b+c}{2}, 0)\\ \shoveleft \implies [TUV]=[ABC]\cdot \begin{vmatrix} 0 & \dfrac{a+b-c}{2} & \dfrac{a-b+c}{2}\\ \dfrac{a+b-c}{2} & 0 & \dfrac{-a+b+c}{2}\\ \dfrac{a-b+c}{2} & \dfrac{-a+b+c}{2} & 0 \end{vmatrix}\\ \shoveleft=[ABC]\cdot \dfrac{(a+b-c)(a-b+c)(-a+b+c)}{4}=[DEF]\blacksquare \end{multline}\)

06/21/2024

$AE$ is the bisector of $\angle{A}$ in right angle $\triangle{ABC}$ and $E$ is on side $BC$, $\angle{C}=90^{\circ}$, $D$ is the midpoint of $AE$, $BC=BD, CE=2$, find $BE$.

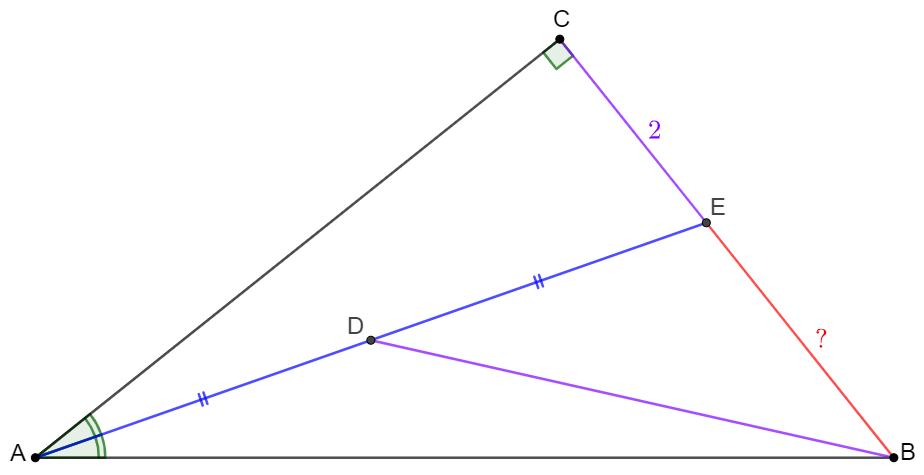
image-20240621170100097

Solve:

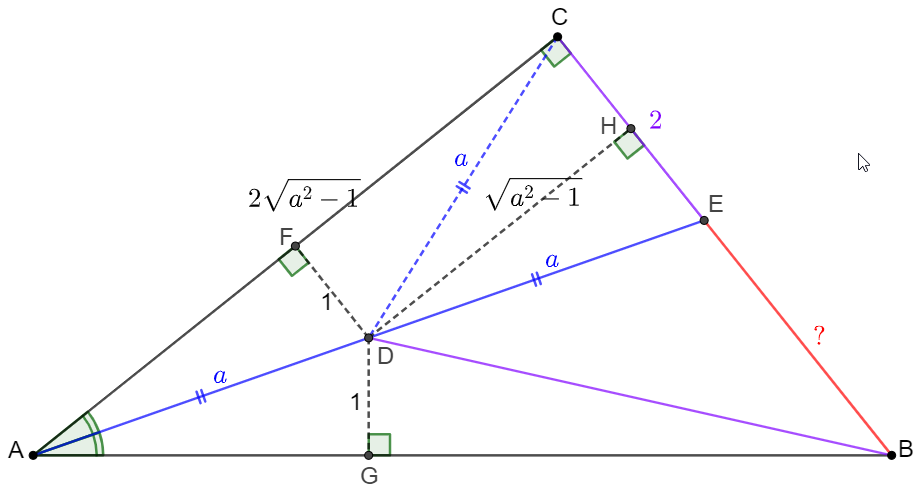image-20240622113214708 \(\begin{multline}\nonumber \shoveleft \text{Make }DF \perp AC \text{ at }F, DG \perp AB \text{ at }G, DH\perp BC \text{ at }H\\ \shoveleft \implies DF=DG=\dfrac{CE}{2}=1, DH=\sqrt{a^2-1}, AC=2\sqrt{a^2-1}\\ \shoveleft \text{Let }AD=DE=CD=a, BC=BD=x, AB=y\\ \shoveleft CD=CE, BC=BD \implies \triangle{CDE} \sim \triangle{CBD}\\ \shoveleft \implies \dfrac{a}{2}=\dfrac{x}{a} \implies x=\dfrac{a^2}{2}\\ \shoveleft [ABC]=[ACD]+[ABD]+[BCD]=\sqrt{a^2-1}+\dfrac{y}{2}+\dfrac{a^2\sqrt{a^2-1}}{4}\\ \shoveleft \implies y=(\dfrac{a^2}{2}-2)\sqrt{a^2-1}\\ \shoveleft AC^2+BC^2=AB^2 \implies 4(a^2-1)+\dfrac{a^4}{4}=(\dfrac{a^2}{2}-2)^2(a^2-1)\\ \shoveleft \implies a^4-10a^2+8=0\implies a^2=5\pm\sqrt{17}\implies BE=\bbox[5px, border: 1px solid black]{\dfrac{1+\sqrt{17}}{2}} \end{multline}\) Solve 2 \(\begin{multline} \shoveleft \text{Let }AD=DE=CD=a, BC=BD=x, \text{ make }DH\perp BC \text{ at }H\\ \shoveleft \text{easy to see }\angle{BAC}=\angle{CDE}=\angle{CBD}, AE \text{ bisects }\angle{BAC} \implies\\ \shoveleft cos\angle{BAC}=\dfrac{AC}{AB}=\dfrac{CE}{BE}=\dfrac{2}{x-2}=cos{\angle{CBD}}=\dfrac{BH}{BD}=\dfrac{x-1}{x}\\ \shoveleft \implies x^2-5x+2=0\implies x=\dfrac{5\pm \sqrt{17}}{2}\implies BE=\bbox[5px, border: 1px solid black]{\dfrac{1+\sqrt{17}}{2}} \end{multline}\)

06/25/2024

A quarter of circle $OAD$ is tangent with line $BC$ and $AB \perp BC, CD \perp BC$, $AB=4, CD=2$, find the area of Circular sector $OAD$

.

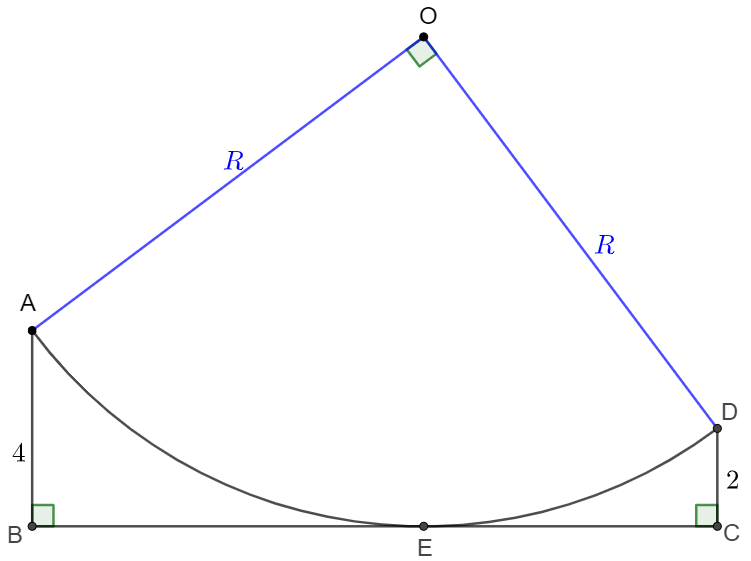
Solve:

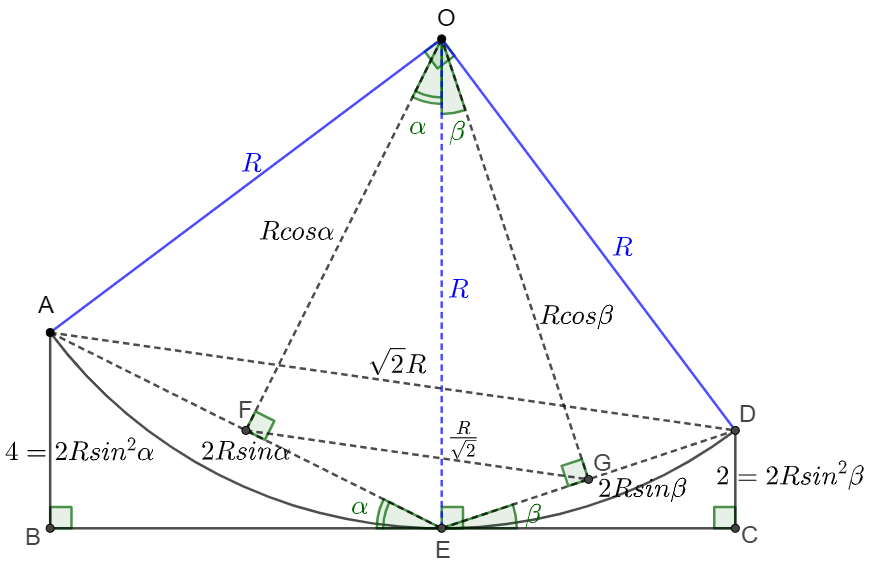image-20240625172205767 \(\begin{multline} \shoveleft \text{Connect }AE, DE, \text{ let }OF \perp AE \text{ at }F, OG \perp DE \text{ at }G\\ \shoveleft \text{Let }\angle{AEB}=\angle{EOF}=\angle{\alpha}, \angle{CED}=\angle{EOG}=\angle{\beta} \implies \\ \shoveleft OF=R\cdot cos\alpha, EF=R\cdot sin\alpha \implies AE=2R\cdot sin\alpha\\ \shoveleft \implies AB=2R\cdot sin^2{\alpha}=4 \implies sin^2{\alpha}=\dfrac{2}{R}\\ \shoveleft OG=R \cdot cos\beta, EG=R\cdot sin\beta \implies DE=2R \cdot sin\beta\\ \shoveleft \implies CD=2R\cdot sin^2{\beta}=2\implies sin^2{\beta}=\dfrac{1}{R}\\ \shoveleft AD=\sqrt{2}R \implies FG=\dfrac{AD}{2}=\dfrac{R}{\sqrt{2}}\\ \shoveleft \angle{AOD}=90^{\circ}\implies \angle{AED}=180^{\circ}-\dfrac{\angle{AOD}}{2}=135^{\circ}\\ \shoveleft \implies cos\angle{AED}=\dfrac{EF^2+EG^2-FG^2}{2\cdot EF \cdot EG}\\ \shoveleft =\dfrac{R^2\cdot sin^2\alpha+R^2 \cdot sin^2\beta-\dfrac{R^2}{2}}{2R^2 \cdot sin\alpha \cdot sin\beta}=-\dfrac{1}{\sqrt{2}} \implies \\ \shoveleft sin\alpha\cdot sin\beta=\dfrac{R-6}{2\sqrt{2}R}\implies sin^2\alpha \cdot sin^2\beta=\dfrac{(R-6)^2}{8R^2}=\dfrac{2}{R^2}\\ \shoveleft \implies (R-6)^2=16\implies R=10 \text{ or }R=2 \text{ (exclude since }sin^2\alpha=\dfrac{2}{R})\\ \shoveleft \implies [O\overset{\huge\frown}{AD}]=\dfrac{\pi \cdot 100}{4}=\bbox[5px, border: 1px solid black]{25 \pi} \end{multline}\) Solve 2:

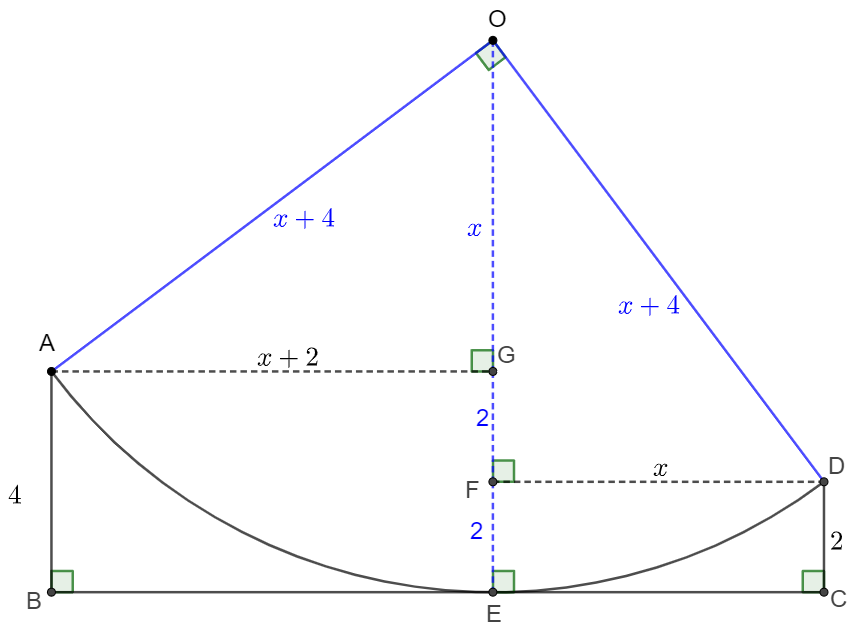image-20240625214143366 \(\begin{multline} \shoveleft \text{Make }DF \perp OE \text{ at }F, AG \perp OE \text{ at }G \implies EF=2, FG=2\\ \shoveleft \text{Let }OG=x, \text{ easy to see } \triangle{AOG}\cong\triangle{DOF}\implies\\ \shoveleft DF=OG=x, AG=OF=x+2, OE=OA=OD=x+4\\ \shoveleft \implies OG^2+AG^2=OA^2\implies x^2+(x+2)^2=(x+4)^2\\ \shoveleft \implies x=6 \implies OA=10\implies [O\overset{\huge\frown}{AD}]=\dfrac{\pi \cdot 100}{4}=\bbox[5px, border: 1px solid black]{25 \pi}\\ \end{multline}\)

    © M∀TH Workout 2020-2021
    Search