05/01/2024
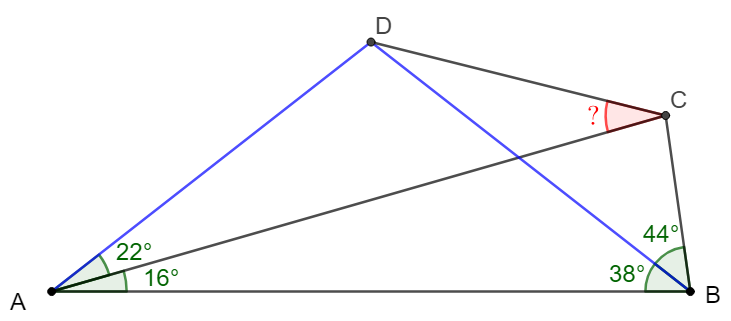
$\angle{BAC}=16^{\circ}, \angle{CAD}=22^{\circ}, \angle{ABD}=38^{\circ}, \angle{CBD}=44^{\circ}$ in quadrilateral $ABCD$, find $\angle{ACD}$.
Solve:
 \(\begin{multline}
\shoveleft \text{Easy to see that }\angle{DAB}=\angle{DBA}=38^{\circ}\implies AD=BD, \angle{ADB}=104^{\circ}, \angle{ACB}=82^{\circ}\\
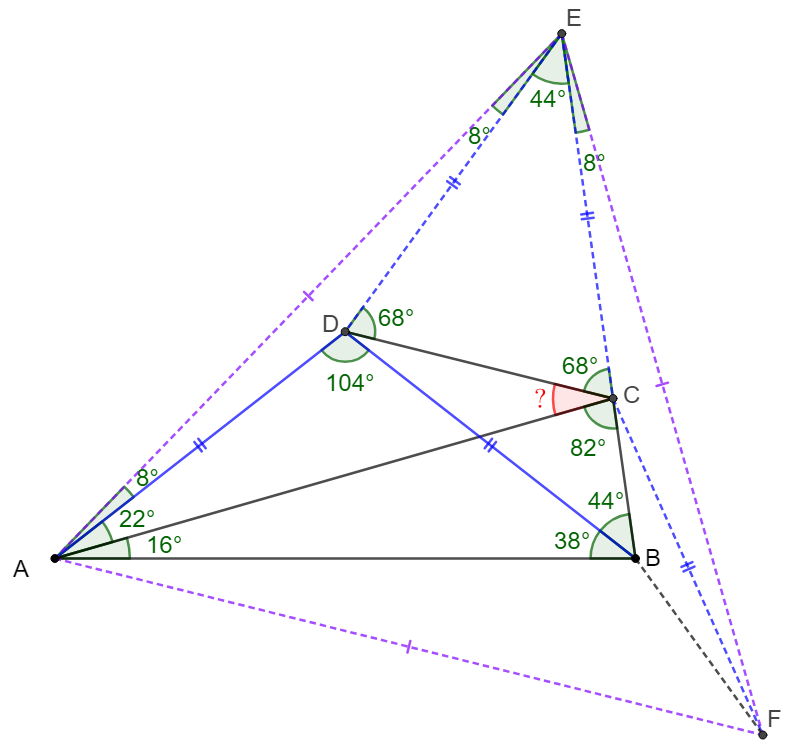
\shoveleft \text{Extend }BC \text{ to }E \text{ such that } \angle{DAE}=8^{\circ} \implies \angle{CAE}=30^{\circ}\implies \angle{AEC}=52^{\circ}=\dfrac{\angle{ADB}}{2}\\
\shoveleft \implies D\text{ is the circumcenter of }\triangle{ABE} \implies AD=DE=DB, \angle{AED}=\angle{DAE}=8^{\circ}\\
\shoveleft \text{Let }F \text{ be the reflection of }E \text{ along line }AC \implies \angle{CAF}=\angle{CAE}=30^{\circ},AE=AF, CE=CF\\
\shoveleft \text{Connect }AF, CF\implies \triangle{AEF} \text{ is equilateral triangle} \implies \angle{CEF}=\angle{CFE}=8^{\circ}=\angle{DAE}\\
\shoveleft \implies \triangle{DAE}\cong\triangle{CEF}\implies DE=CE\implies \angle{ECD}=\angle{EDC}=\dfrac{180^{\circ}-44^{\circ}}{2}=68^{\circ}\\
\shoveleft \implies \angle{ACD}=180^{\circ}-82^{\circ}-68^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Easy to see that }\angle{DAB}=\angle{DBA}=38^{\circ}\implies AD=BD, \angle{ADB}=104^{\circ}, \angle{ACB}=82^{\circ}\\
\shoveleft \text{Extend }BC \text{ to }E \text{ such that } \angle{DAE}=8^{\circ} \implies \angle{CAE}=30^{\circ}\implies \angle{AEC}=52^{\circ}=\dfrac{\angle{ADB}}{2}\\
\shoveleft \implies D\text{ is the circumcenter of }\triangle{ABE} \implies AD=DE=DB, \angle{AED}=\angle{DAE}=8^{\circ}\\
\shoveleft \text{Let }F \text{ be the reflection of }E \text{ along line }AC \implies \angle{CAF}=\angle{CAE}=30^{\circ},AE=AF, CE=CF\\
\shoveleft \text{Connect }AF, CF\implies \triangle{AEF} \text{ is equilateral triangle} \implies \angle{CEF}=\angle{CFE}=8^{\circ}=\angle{DAE}\\
\shoveleft \implies \triangle{DAE}\cong\triangle{CEF}\implies DE=CE\implies \angle{ECD}=\angle{EDC}=\dfrac{180^{\circ}-44^{\circ}}{2}=68^{\circ}\\
\shoveleft \implies \angle{ACD}=180^{\circ}-82^{\circ}-68^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
05/02/2024
Factorize $x^6-4x^3-1$
Solve: \(\begin{multline} \shoveleft \text{Suppose there is }a \text{ such that } x^6-4x^3-1=x^6-ax^3+(a-4)x^3-1\\ \shoveleft =x^3(x^3-a)+(a-4)x^3-1 \text{ and we hope }\dfrac{1}{a}=\dfrac{a-4}{1}=k\\ \shoveleft \implies a^2-4a-1=0\implies a=2\pm \sqrt{5} \implies a-4=-2\pm\sqrt{5}\\ \shoveleft \implies k=\dfrac{1}{2\pm\sqrt{5}}=\dfrac{2\mp\sqrt{5}}{-1}=-2\pm\sqrt{5}\\ \shoveleft \implies x^6-4x^3-1=x^6-ax^3+kx^3-ak=(x^3+k)(x^3-a)\\ \shoveleft =\bbox[5px, border: 1px solid black]{(x^3-2+\sqrt{5})(x^3-2-\sqrt{5})}\\ \end{multline}\)
05/08/2024
Solve cubic equation: $x^3=3ax^2+6bx+2c$
Solve: \(\begin{multline} \shoveleft x^3=3ax^2+6bx+2c\\ \shoveleft \text{Let }x=y+a \implies (y+a)^3=3a(y+a)^2+6b(y+a)+2c\\ \shoveleft \implies y^3+3ay^2+3a^2y+a^3=3ay^2+6a^2y+3a^3+6by+6ab+2c\\ \shoveleft \implies y^3=3(a^2+2b)y+2(a^3+3ab+c)\\ \shoveleft \text{Let }p=a^2+2b, q=a^3+3ab+c \implies y^3=3py+2q\\ \shoveleft u_1=q+\sqrt[3]{q^2-p^3}, u_2=q-\sqrt[3]{q^2-p^3}\\ \shoveleft \omega_1=\dfrac{-1+\sqrt{3}i}{2}, \omega_2=\omega_1^2=\dfrac{-1-\sqrt{3}i}{2}\\ \shoveleft \begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix}= \begin{bmatrix} 1 & 1\\ \omega & \omega^2\\ \omega^2 & \omega \end{bmatrix} \cdot \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} \implies \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}= \begin{bmatrix} 1 & 1 & 1\\ \omega & \omega^2 & 1\\ \omega^2 & \omega & 1 \end{bmatrix} \cdot \begin{bmatrix} u_1 \\ u_2 \\ a \end{bmatrix} = \begin{bmatrix} u_1+u_2+a\\ \omega_1\cdot u_1+\omega_2\cdot u_2+a\\ \omega_2 \cdot u_1 + \omega_1 \cdot u_2+a\\ \end{bmatrix}\\ \shoveleft \text{Summary: }\\ \shoveleft x^3=3ax^2+6bx+2c \implies\\ \shoveleft p=a^2+2b, q=a^3+3ab+c\\ \shoveleft u_1=q+\sqrt[3]{q^2-p^3}, u_2=q-\sqrt[3]{q^2-p^3}\\ \shoveleft \implies \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}= \begin{bmatrix} 1 & 1 & 1\\ \omega & \omega^2 & 1\\ \omega^2 & \omega & 1 \end{bmatrix} \cdot \begin{bmatrix} u_1 \\ u_2 \\ a \end{bmatrix} \end{multline}\)
Note: \(\begin{multline} \shoveleft \text{Quadratic equation:}\\ \shoveleft x^2=2px+q \implies x=p \pm \sqrt{p^2+q}\\ \end{multline}\)
05/10/2024
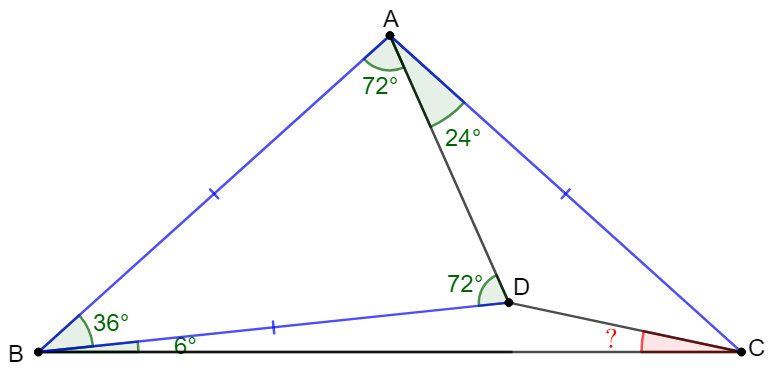
$D$ is a point inside $\triangle{ABC}$ such that $\angle{BAD}=72^{\circ}$, $\angle{CAD}=24^{\circ}$, $\angle{CBD}=6^{\circ}$, find $\angle{BCD}$.
Solve:
 \(\begin{multline}
\shoveleft \text{Easy to see that }\\
\shoveleft \angle{ACB}=42^{\circ}=\angle{ABC}\implies AB=AC\\
\shoveleft \angle{ADB}=72^{\circ}=\angle{BAD}\implies AB=BD\\
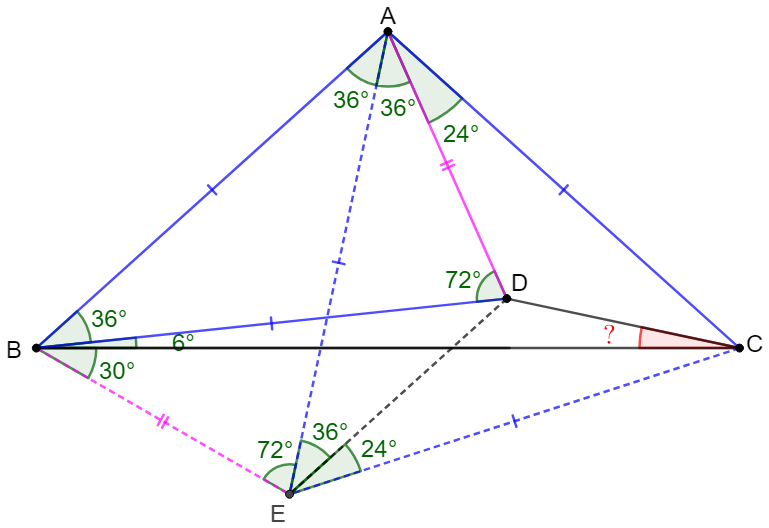
\shoveleft \text{Make }E\text{ on bisector of }\angle{BAD} \text{ such that }AB=AE\\
\shoveleft \implies \triangle{ABE}\cong\triangle{ABD}, \angle{AEB}=\angle{ABE}=72^{\circ}\\
\shoveleft \implies ABED \text{ are cyclic} \implies \angle{AED}=\angle{ABD}=36^{\circ}\\
\shoveleft \angle{EAC}=60^{\circ}, AE=AB=AC\implies \triangle{ACE}\text{ is equilateral}\\
\shoveleft \implies AC=CE, \angle{AEC}=60^{\circ}\implies \angle{CED}=24^{\circ}=\angle{CAD}\\
\shoveleft \implies \triangle{CAD}\cong\triangle{CED} \implies \angle{ACD}=\angle{ECD}=30^{\circ}\\
\shoveleft \implies \angle{BCD}=42^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{12^{\circ}}\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Easy to see that }\\
\shoveleft \angle{ACB}=42^{\circ}=\angle{ABC}\implies AB=AC\\
\shoveleft \angle{ADB}=72^{\circ}=\angle{BAD}\implies AB=BD\\
\shoveleft \text{Make }E\text{ on bisector of }\angle{BAD} \text{ such that }AB=AE\\
\shoveleft \implies \triangle{ABE}\cong\triangle{ABD}, \angle{AEB}=\angle{ABE}=72^{\circ}\\
\shoveleft \implies ABED \text{ are cyclic} \implies \angle{AED}=\angle{ABD}=36^{\circ}\\
\shoveleft \angle{EAC}=60^{\circ}, AE=AB=AC\implies \triangle{ACE}\text{ is equilateral}\\
\shoveleft \implies AC=CE, \angle{AEC}=60^{\circ}\implies \angle{CED}=24^{\circ}=\angle{CAD}\\
\shoveleft \implies \triangle{CAD}\cong\triangle{CED} \implies \angle{ACD}=\angle{ECD}=30^{\circ}\\
\shoveleft \implies \angle{BCD}=42^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{12^{\circ}}\\
\end{multline}\)
05/12/2024
$D$ is a point inside $\triangle{ABC}$ such that $\angle{BAD}=12^{\circ}$, $\angle{CAD}=36^{\circ}$, $\angle{ABD}=42^{\circ}$, $\angle{CBD}=12^{\circ}$, find $\angle{BCD}$.
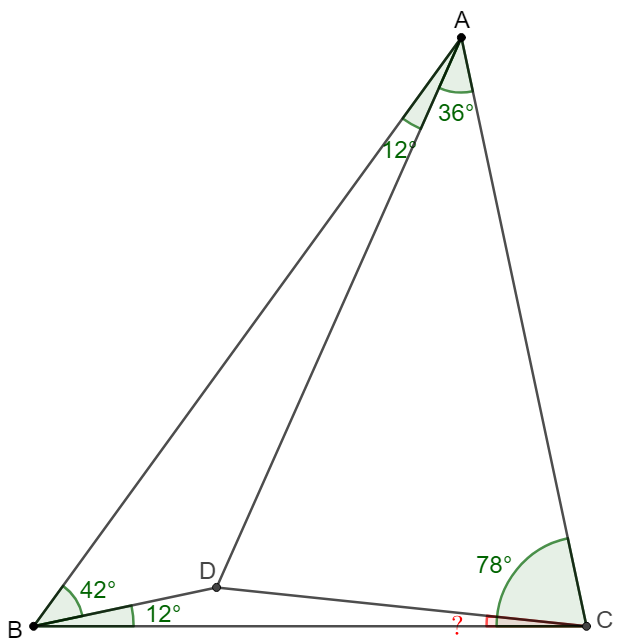
Solve:
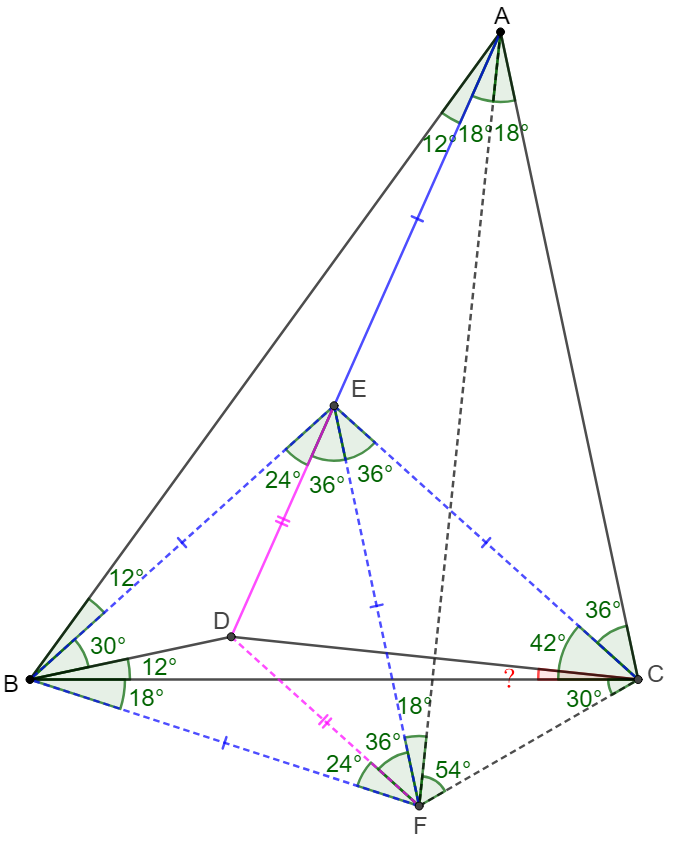 \(\begin{multline}
\shoveleft \text{Let }E \text{ on }AD \text{ such that }\angle{ABE}=\angle{BAE}=12^{\circ}\\
\shoveleft \implies AE=BE, \angle{DBE}=30^{\circ},\angle{AEB}=156^{\circ}=2\angle{ACB}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies AE=BE=CE,\angle{AEC}=2\angle{ABC}=108^{\circ}\\
\shoveleft \text{Let }F \text{ be the reflection of }E \text{ along }BD \\
\shoveleft \implies BE=BF, DE=DF, \angle{BED}=\angle{BFD}=24^{\circ},\angle{FBD}=\angle{EBD}=30^{\circ}\\
\shoveleft \implies \triangle{BEF} \text{ is equilateral}\implies \angle{DEF}=\angle{DFE}=36^{\circ},AE=BE=CE=FE\\
\shoveleft \implies \angle{EAF}=\angle{EFA}=18^{\circ}, ABCF \text{ is cyclic }\\
\shoveleft \implies \angle{AFC}=\angle{ABC}=54^{\circ}, \angle{BCF}=\angle{BAF}=30^{\circ}\\
\shoveleft \implies \angle{DFC}=108^{\circ}=\angle{AEC} \implies DECF \text{ is cyclic}\\
\shoveleft \implies \angle{DCF}=\angle{DEF}=36^{\circ}\implies \angle{BCD}=\angle{DCF}-\angle{BCF}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ on }AD \text{ such that }\angle{ABE}=\angle{BAE}=12^{\circ}\\
\shoveleft \implies AE=BE, \angle{DBE}=30^{\circ},\angle{AEB}=156^{\circ}=2\angle{ACB}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ABC}\\
\shoveleft \implies AE=BE=CE,\angle{AEC}=2\angle{ABC}=108^{\circ}\\
\shoveleft \text{Let }F \text{ be the reflection of }E \text{ along }BD \\
\shoveleft \implies BE=BF, DE=DF, \angle{BED}=\angle{BFD}=24^{\circ},\angle{FBD}=\angle{EBD}=30^{\circ}\\
\shoveleft \implies \triangle{BEF} \text{ is equilateral}\implies \angle{DEF}=\angle{DFE}=36^{\circ},AE=BE=CE=FE\\
\shoveleft \implies \angle{EAF}=\angle{EFA}=18^{\circ}, ABCF \text{ is cyclic }\\
\shoveleft \implies \angle{AFC}=\angle{ABC}=54^{\circ}, \angle{BCF}=\angle{BAF}=30^{\circ}\\
\shoveleft \implies \angle{DFC}=108^{\circ}=\angle{AEC} \implies DECF \text{ is cyclic}\\
\shoveleft \implies \angle{DCF}=\angle{DEF}=36^{\circ}\implies \angle{BCD}=\angle{DCF}-\angle{BCF}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
05/13/2024
$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=\angle{CBD}=6^{\circ}$, $\angle{ACD}=18^{\circ}$, $\angle{BCD}=12^{\circ}$, find $\angle{BAD}$.
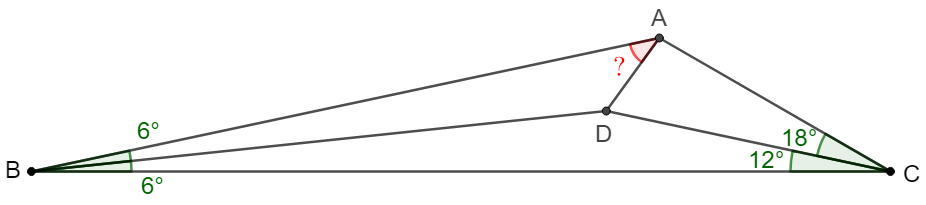
Solve:
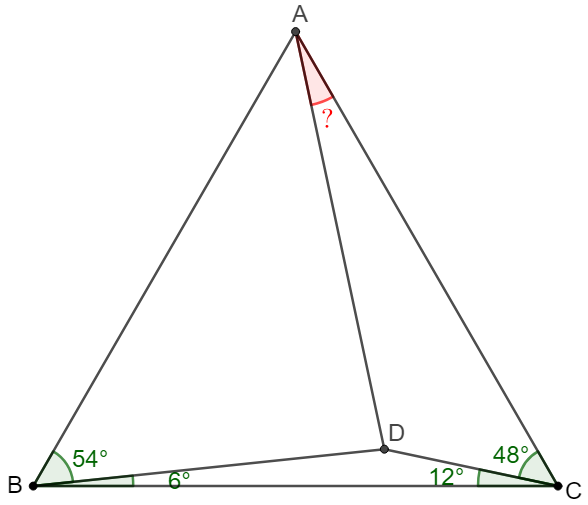
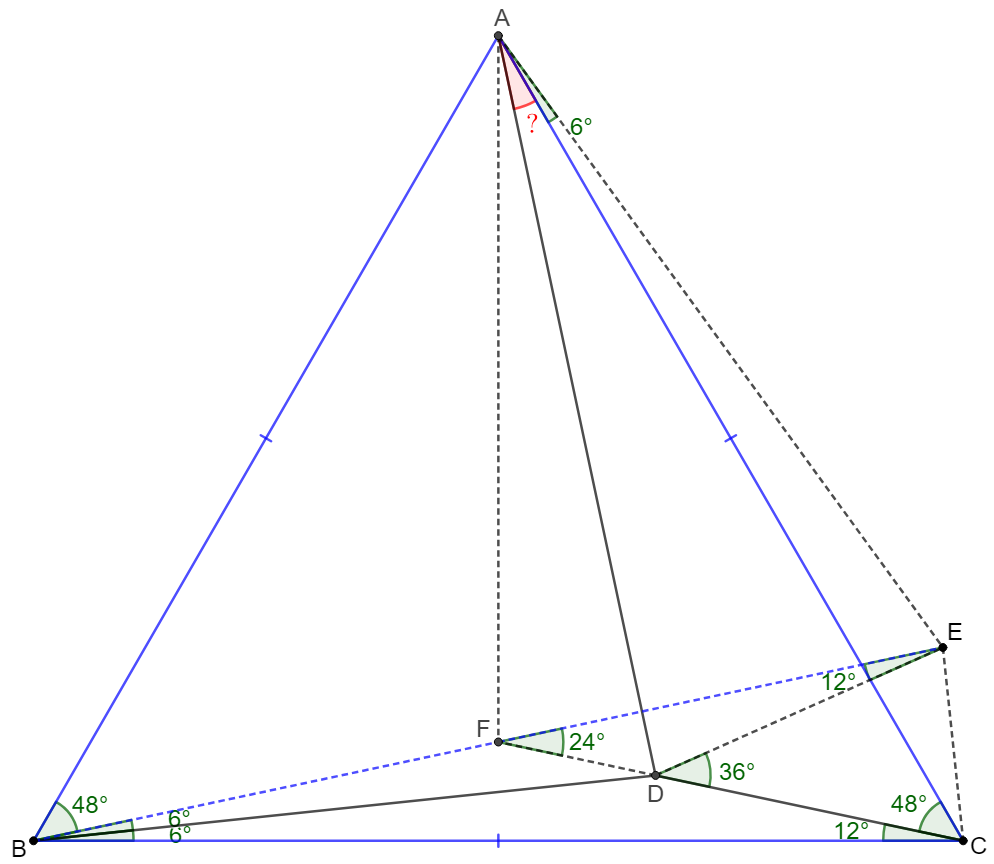
\(\begin{multline}
\shoveleft \text{First we need prove a related problem: }D \text{ is a point in equilateral }\\
\shoveleft \triangle{ABC} \text{ such that }\angle{BCD}=12^{\circ}, \angle{CBD}=6^{\circ}, \text{ find }\angle{CAD}:
\end{multline}\)
 \(\begin{multline}
\shoveleft \text{Make }E \text{ be the reflect of }C \text{ along the line }BD \implies \\
\shoveleft CD=DE,BC=BE, \angle{BCD}=\angle{BED}=6^{\circ}, \angle{BCD}=\angle{BED}=12^{\circ}\\
\shoveleft \implies \angle{BAE}=\angle{BEA}=\dfrac{180^{\circ}-\angle{ABE}}{2}=\dfrac{180^{\circ}-48^{\circ}}{2}=66^{\circ}\implies \angle{CAE}=6^{\circ}\\
\shoveleft \text{Extend }CD \text{ and intersect }BE \text{ at }F \implies \angle{BCF}=\angle{CBF}=12^{\circ}\implies \\
\shoveleft \begin{cases}
BF=CF\implies \triangle{ABF}\cong\triangle{ACF}\implies \angle{CAF}=30^{\circ}\implies \angle{EAF}=36^{\circ}\\
\angle{CFE}=24^{\circ} \implies \angle{CDE}=36^{\circ}=\angle{EAF}\\
\end{cases}\\
\shoveleft \implies AFDE \text{ is cyclic }\implies \angle{DAE}=\angle{DFE}=24^{\circ}\implies \angle{DAC}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }E \text{ be the reflect of }C \text{ along the line }BD \implies \\
\shoveleft CD=DE,BC=BE, \angle{BCD}=\angle{BED}=6^{\circ}, \angle{BCD}=\angle{BED}=12^{\circ}\\
\shoveleft \implies \angle{BAE}=\angle{BEA}=\dfrac{180^{\circ}-\angle{ABE}}{2}=\dfrac{180^{\circ}-48^{\circ}}{2}=66^{\circ}\implies \angle{CAE}=6^{\circ}\\
\shoveleft \text{Extend }CD \text{ and intersect }BE \text{ at }F \implies \angle{BCF}=\angle{CBF}=12^{\circ}\implies \\
\shoveleft \begin{cases}
BF=CF\implies \triangle{ABF}\cong\triangle{ACF}\implies \angle{CAF}=30^{\circ}\implies \angle{EAF}=36^{\circ}\\
\angle{CFE}=24^{\circ} \implies \angle{CDE}=36^{\circ}=\angle{EAF}\\
\end{cases}\\
\shoveleft \implies AFDE \text{ is cyclic }\implies \angle{DAE}=\angle{DFE}=24^{\circ}\implies \angle{DAC}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
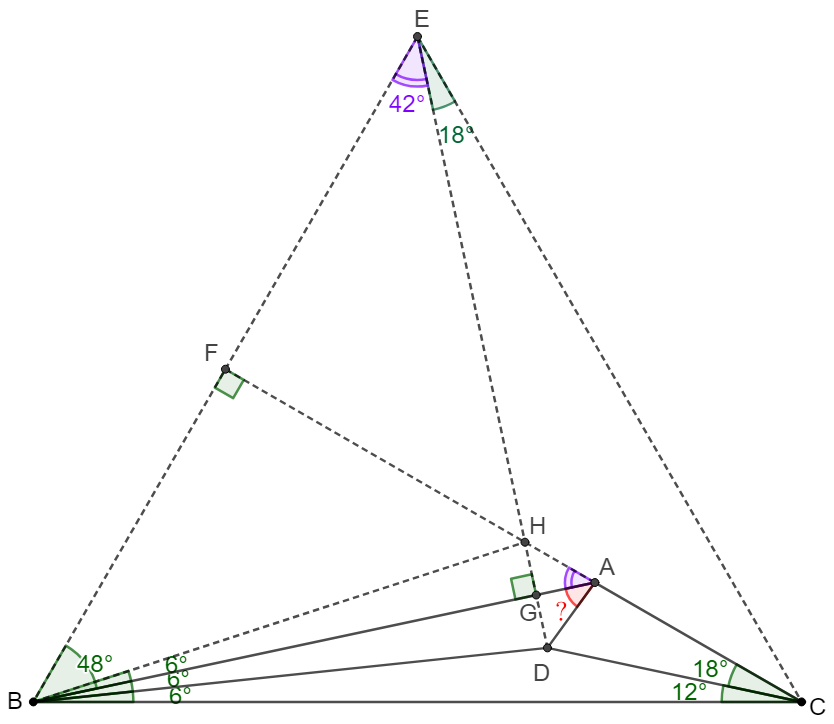 \(\begin{multline}
\shoveleft \text{Make }\triangle{EBC} \text{ be an equilateral triangle}\\
\shoveleft \implies \angle{DEC}=18^{\circ} \implies \angle{BED}=42^{\circ}\\
\shoveleft \text{And we know }\angle{ABE}=48^{\circ} \implies BA\perp DE, \text{ suppose }BA\cap DE=G \\
\shoveleft \text{Extend }CA \text{ to }F\text{ on }BE, \angle{BAF}=30^{\circ} \implies CF \perp BE, BF=FE\\
\shoveleft \text{Make }H \text{ on }AF \text{ such that }\angle{ABH}=6^{\circ} \implies \angle{ABH}=42^{\circ}\\
\shoveleft \triangle{BFH}\cong\triangle{EFH}\implies BH=EH\implies \angle{FEH}=42^{\circ}=\angle{BED}\\
\shoveleft \implies EHGD \text{ are collinear} \implies BD=BH \implies \triangle{ABD}\cong\triangle{ABH}\\
\shoveleft \implies \angle{BAD}=\angle{BAH}=90^{\circ}-\angle{AHG}=90^{\circ}-\angle{EHF}=\angle{FEH}=\bbox[5px, border: 1px solid black]{42^{\circ}}\\
\shoveleft
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }\triangle{EBC} \text{ be an equilateral triangle}\\
\shoveleft \implies \angle{DEC}=18^{\circ} \implies \angle{BED}=42^{\circ}\\
\shoveleft \text{And we know }\angle{ABE}=48^{\circ} \implies BA\perp DE, \text{ suppose }BA\cap DE=G \\
\shoveleft \text{Extend }CA \text{ to }F\text{ on }BE, \angle{BAF}=30^{\circ} \implies CF \perp BE, BF=FE\\
\shoveleft \text{Make }H \text{ on }AF \text{ such that }\angle{ABH}=6^{\circ} \implies \angle{ABH}=42^{\circ}\\
\shoveleft \triangle{BFH}\cong\triangle{EFH}\implies BH=EH\implies \angle{FEH}=42^{\circ}=\angle{BED}\\
\shoveleft \implies EHGD \text{ are collinear} \implies BD=BH \implies \triangle{ABD}\cong\triangle{ABH}\\
\shoveleft \implies \angle{BAD}=\angle{BAH}=90^{\circ}-\angle{AHG}=90^{\circ}-\angle{EHF}=\angle{FEH}=\bbox[5px, border: 1px solid black]{42^{\circ}}\\
\shoveleft
\end{multline}\)
05/14/2024
We can see from the above problem that, by applying Ceva’s theorem in angle form, $\dfrac{sin6^{\circ}}{sin54^{\circ}}\cdot\dfrac{sin42^{\circ}}{sin18^{\circ}}\cdot\dfrac{sin48^{\circ}}{sin12^{\circ}}=1$, and the order of the angles can be different thus lead to 2 situations:
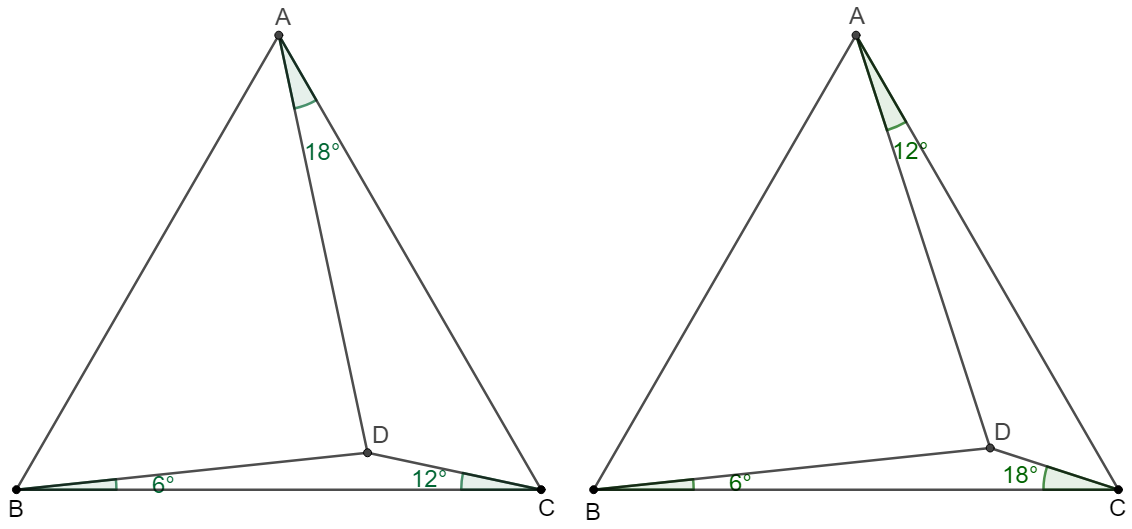
For each of the situations (we call them: “6-with-12” and “6-with-18”), the unknown angle can be chosen from $6^{\circ}, 12^{\circ}$ or $18^{\circ}$, thus making totally 6 problems
(1) 6-with-12, unknown=6
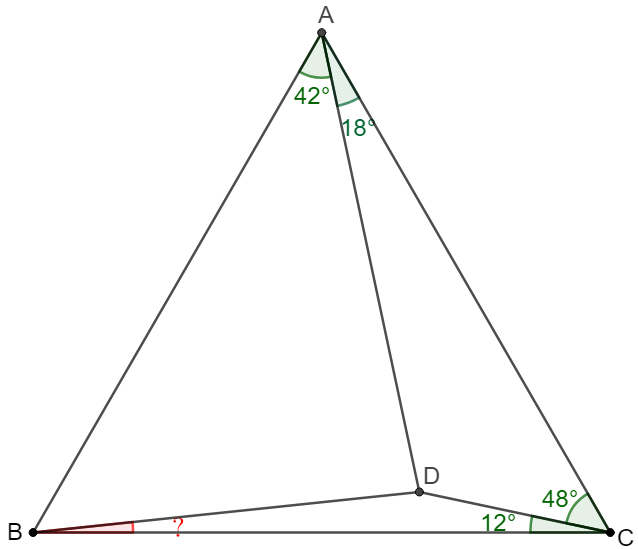
Solve:
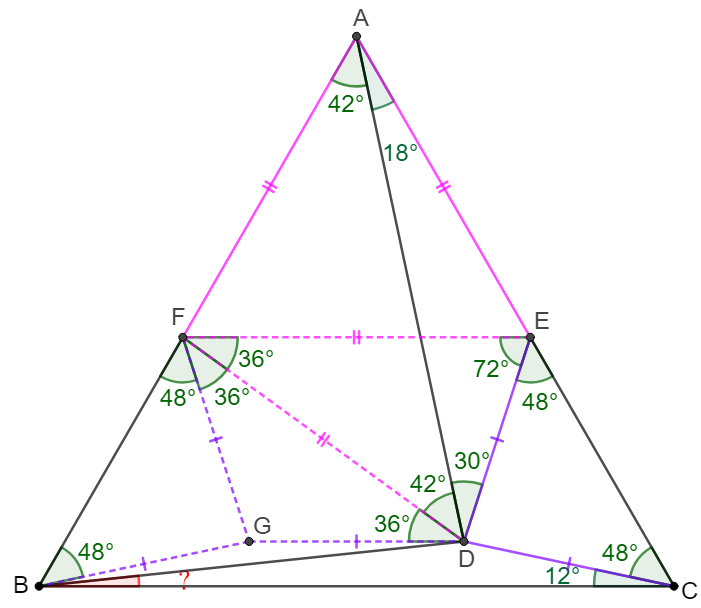 \(\begin{multline}
\shoveleft \text{Make }E \text{ on }AC \text{ such that }CD=DE\\
\shoveleft \implies \angle{DEC}=\angle{DCE}=48^{\circ}, \angle{CDE}=84^{\circ}\\
\shoveleft \implies \angle{ADE}=180^{\circ}-18^{\circ}-84^{\circ}-48^{\circ}=30^{\circ}\\
\shoveleft \text{Make }EF \parallel BC \implies AEF \text{ is equilateral}\\
\shoveleft \implies AE=EF,\angle{AEF}=60^{\circ}=2\angle{ADE}\\
\shoveleft \implies F \text{ is circumcenter of }\triangle{ADE}\implies\\
\shoveleft DF=EF, \angle{DFE}=2\angle{DAE}=36^{\circ}\\
\shoveleft \implies \angle{DEF}=72^{\circ}=\angle{EDF}\implies \angle{ADF}=42^{\circ}\\
\shoveleft \text{Make }G \text{ satisfying } GF=BG, \angle{BFG}=\angle{FBG}=48^{\circ}\\
\shoveleft \implies \angle{DFG}=180^{\circ}-60^{\circ}-48^{\circ}-36^{\circ}=36^{\circ}\\
\shoveleft BF=CE\implies \triangle{BFG}
\cong\triangle{CED}\implies GF=DE\\
\shoveleft \implies DEFG \text{ is isosceles trapezoid }\implies DG\parallel EF\\
\shoveleft \implies \angle{FDG}=\angle{DFE}=36^{\circ}=\angle{DFG}\\
\shoveleft \implies BG=GF=GD \implies G \text{ is circumcenter of }\triangle{BDF}\\
\shoveleft \implies \angle{BGD}=2\angle{BFD}=2(48^{\circ}+36^{\circ})=168^{\circ}\\
\shoveleft \implies \angle{BDG}=\angle{DBG}=6^{\circ}\implies \angle{CBD}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }E \text{ on }AC \text{ such that }CD=DE\\
\shoveleft \implies \angle{DEC}=\angle{DCE}=48^{\circ}, \angle{CDE}=84^{\circ}\\
\shoveleft \implies \angle{ADE}=180^{\circ}-18^{\circ}-84^{\circ}-48^{\circ}=30^{\circ}\\
\shoveleft \text{Make }EF \parallel BC \implies AEF \text{ is equilateral}\\
\shoveleft \implies AE=EF,\angle{AEF}=60^{\circ}=2\angle{ADE}\\
\shoveleft \implies F \text{ is circumcenter of }\triangle{ADE}\implies\\
\shoveleft DF=EF, \angle{DFE}=2\angle{DAE}=36^{\circ}\\
\shoveleft \implies \angle{DEF}=72^{\circ}=\angle{EDF}\implies \angle{ADF}=42^{\circ}\\
\shoveleft \text{Make }G \text{ satisfying } GF=BG, \angle{BFG}=\angle{FBG}=48^{\circ}\\
\shoveleft \implies \angle{DFG}=180^{\circ}-60^{\circ}-48^{\circ}-36^{\circ}=36^{\circ}\\
\shoveleft BF=CE\implies \triangle{BFG}
\cong\triangle{CED}\implies GF=DE\\
\shoveleft \implies DEFG \text{ is isosceles trapezoid }\implies DG\parallel EF\\
\shoveleft \implies \angle{FDG}=\angle{DFE}=36^{\circ}=\angle{DFG}\\
\shoveleft \implies BG=GF=GD \implies G \text{ is circumcenter of }\triangle{BDF}\\
\shoveleft \implies \angle{BGD}=2\angle{BFD}=2(48^{\circ}+36^{\circ})=168^{\circ}\\
\shoveleft \implies \angle{BDG}=\angle{DBG}=6^{\circ}\implies \angle{CBD}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
(2) 6-with-12, unknown=12 – has been solved Feb 2023 and copied here:
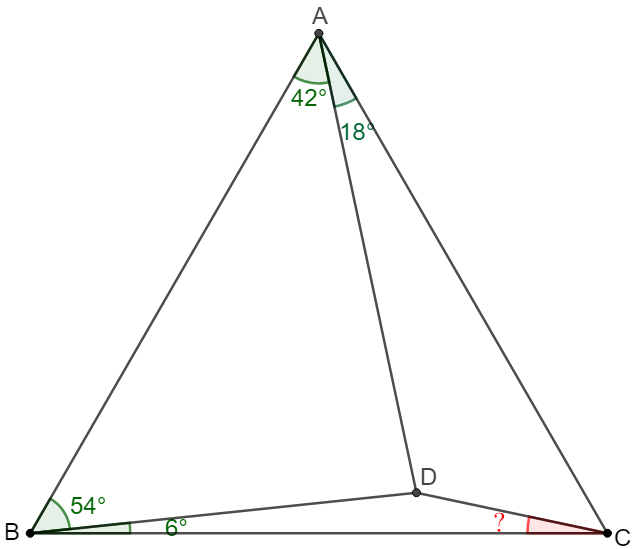
Solve:
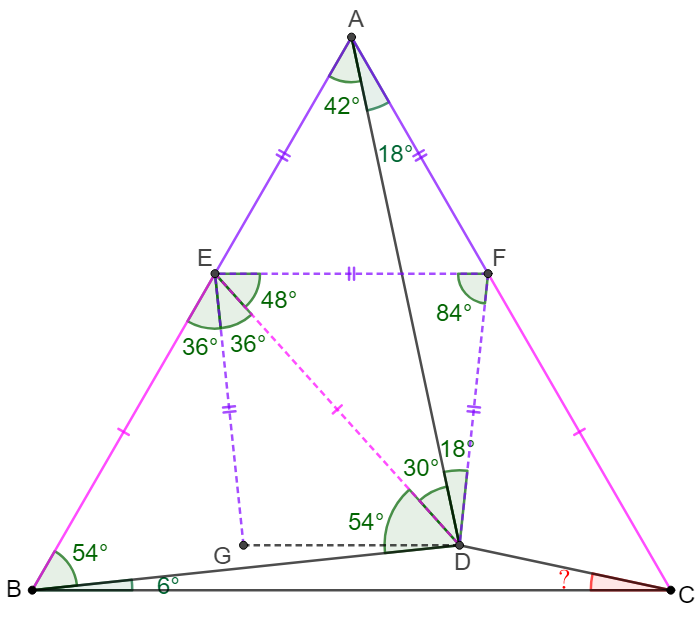 \(\begin{multline}
\shoveleft \text{Make }E \text{ on }AB \text{ such that }\angle{BDE}=\angle{DBE}=54^{\circ}\\
\shoveleft \implies BE=DE, \angle{DEG}=\angle{BEG}=36^{\circ}\\
\shoveleft \angle{ADE}=180^{\circ}-54^{\circ}-54^{\circ}-42^{\circ}=30^{\circ}\\
\shoveleft \text{Make }EF \parallel BC \implies \triangle{AEF}\text{ is equilateral}\\
\shoveleft \implies AE=EF, BE=CF=DE, \angle{AFE}=60^{\circ}=2\angle{ADE}\\
\shoveleft \implies F\text{ is the circumcenter of }\triangle{ADE}\\
\shoveleft \implies EF=DF=EG,\angle{EFD}=2\angle{EAD}=84^{\circ}=\angle{FEG}\\
\shoveleft \implies EFDG\text{ is isosceles trapezoid }\implies EF\parallel DG\\
\shoveleft \implies \angle{ACD}=angle{ABG}=\angle{EDG}=\angle{DEF}=48^{\circ}\\
\shoveleft \implies \angle{BCD}=60^{\circ}-48^{\circ}=\bbox[5px, border: 1px solid black]{12^{\circ}}\\
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }E \text{ on }AB \text{ such that }\angle{BDE}=\angle{DBE}=54^{\circ}\\
\shoveleft \implies BE=DE, \angle{DEG}=\angle{BEG}=36^{\circ}\\
\shoveleft \angle{ADE}=180^{\circ}-54^{\circ}-54^{\circ}-42^{\circ}=30^{\circ}\\
\shoveleft \text{Make }EF \parallel BC \implies \triangle{AEF}\text{ is equilateral}\\
\shoveleft \implies AE=EF, BE=CF=DE, \angle{AFE}=60^{\circ}=2\angle{ADE}\\
\shoveleft \implies F\text{ is the circumcenter of }\triangle{ADE}\\
\shoveleft \implies EF=DF=EG,\angle{EFD}=2\angle{EAD}=84^{\circ}=\angle{FEG}\\
\shoveleft \implies EFDG\text{ is isosceles trapezoid }\implies EF\parallel DG\\
\shoveleft \implies \angle{ACD}=angle{ABG}=\angle{EDG}=\angle{DEF}=48^{\circ}\\
\shoveleft \implies \angle{BCD}=60^{\circ}-48^{\circ}=\bbox[5px, border: 1px solid black]{12^{\circ}}\\
\end{multline}\)
(3) 6-with-12, unknown=18 – this has been solved above
(4) 6-with-18, unknown=6 – this has been solved in April 2022
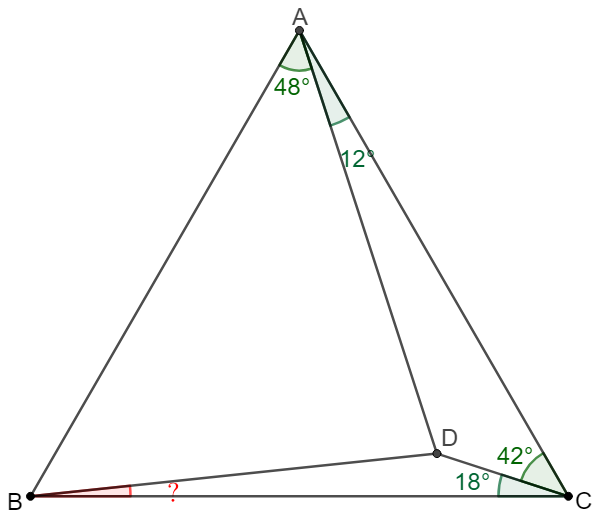
Solve:
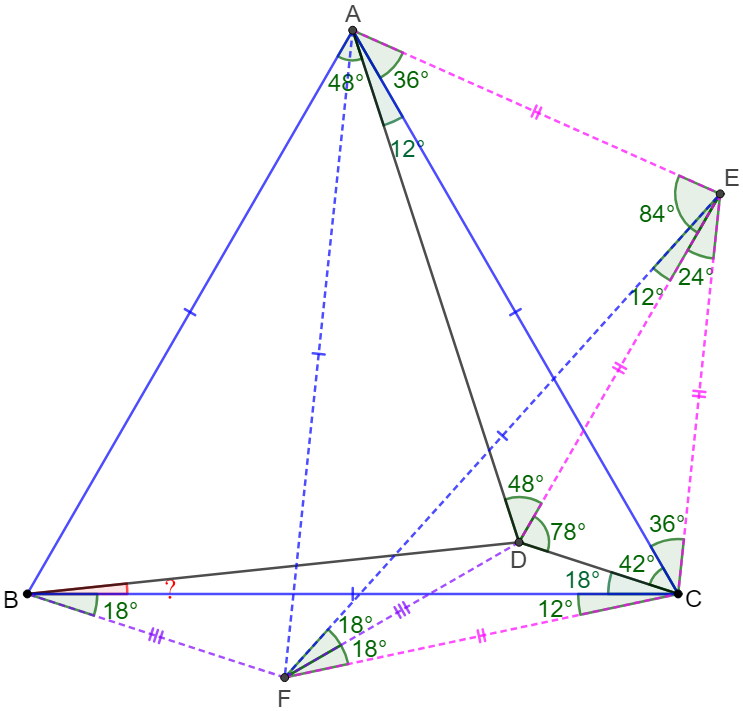 \(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of } \triangle{ACD} \implies\\
\shoveleft AE=CE=DE, \angle{CED}=2\angle{CAD}=24^{\circ} \implies \\
\shoveleft \angle{ECD}=\angle{EDC}=78^{\circ}\implies \angle{ACE}=36^{\circ} \implies \\
\shoveleft \angle{CAE}=36^{\circ}\implies \angle{AEC}=108^{\circ} \implies \angle{AED}=84^{\circ}\\
\shoveleft \text{Find }F \text{ such that }\angle{ECF}=\angle{AEC}=108^{\circ}, CE=CF \implies\\
\shoveleft \text{(1) }\angle{BCF}=108^{\circ}-60^{\circ}-36^{\circ}=12^{\circ}, \text{(2) }\triangle{AEC}\cong \triangle{ECF}\\
\shoveleft \implies EF=AC=BC, \angle{CEF}=\angle{CFE}=36^{\circ}, \angle{ACF}=72^{\circ}\\
\shoveleft \implies \angle{DEF=12^{\circ}}=\angle{BCF}\implies \triangle{BCF} \cong\triangle{FED}\\
\shoveleft \implies \angle{FBC}=\angle{DFE},BF=DF \implies \angle{FBD}=\angle{FDB}\\
\shoveleft \text{At mean time, }\angle{CFE}=\angle{CAE}\implies AECF\text{ is cyclic}\\
\shoveleft \implies \angle{AFC}=180^{\circ}-\angle{AEC}=72^{\circ}=\angle{ACF}\implies\\
\shoveleft \angle{FAC}=36^{\circ}, AF=AC=AB \implies A \text{ is the circumcenter of }\triangle{BCF}\\
\shoveleft \implies \angle{FBC}=\dfrac{\angle{FAC}}{2}=18^{\circ}=\angle{DFE}\implies \angle{CFD}=36^{\circ}-18^{\circ}=18^{\circ}\\
\shoveleft \angle{BFD}=180^{\circ}-18^{\circ}-12^{\circ}-18^{\circ}=132^{\circ}\implies \angle{FBD}=\angle{FDB}=24^{\circ}\\
\shoveleft \implies \angle{CBD}=24^{\circ}-18^{\circ}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ be the circumcenter of } \triangle{ACD} \implies\\
\shoveleft AE=CE=DE, \angle{CED}=2\angle{CAD}=24^{\circ} \implies \\
\shoveleft \angle{ECD}=\angle{EDC}=78^{\circ}\implies \angle{ACE}=36^{\circ} \implies \\
\shoveleft \angle{CAE}=36^{\circ}\implies \angle{AEC}=108^{\circ} \implies \angle{AED}=84^{\circ}\\
\shoveleft \text{Find }F \text{ such that }\angle{ECF}=\angle{AEC}=108^{\circ}, CE=CF \implies\\
\shoveleft \text{(1) }\angle{BCF}=108^{\circ}-60^{\circ}-36^{\circ}=12^{\circ}, \text{(2) }\triangle{AEC}\cong \triangle{ECF}\\
\shoveleft \implies EF=AC=BC, \angle{CEF}=\angle{CFE}=36^{\circ}, \angle{ACF}=72^{\circ}\\
\shoveleft \implies \angle{DEF=12^{\circ}}=\angle{BCF}\implies \triangle{BCF} \cong\triangle{FED}\\
\shoveleft \implies \angle{FBC}=\angle{DFE},BF=DF \implies \angle{FBD}=\angle{FDB}\\
\shoveleft \text{At mean time, }\angle{CFE}=\angle{CAE}\implies AECF\text{ is cyclic}\\
\shoveleft \implies \angle{AFC}=180^{\circ}-\angle{AEC}=72^{\circ}=\angle{ACF}\implies\\
\shoveleft \angle{FAC}=36^{\circ}, AF=AC=AB \implies A \text{ is the circumcenter of }\triangle{BCF}\\
\shoveleft \implies \angle{FBC}=\dfrac{\angle{FAC}}{2}=18^{\circ}=\angle{DFE}\implies \angle{CFD}=36^{\circ}-18^{\circ}=18^{\circ}\\
\shoveleft \angle{BFD}=180^{\circ}-18^{\circ}-12^{\circ}-18^{\circ}=132^{\circ}\implies \angle{FBD}=\angle{FDB}=24^{\circ}\\
\shoveleft \implies \angle{CBD}=24^{\circ}-18^{\circ}=\bbox[5px, border: 1px solid black]{6^{\circ}}
\end{multline}\)
(5) 6-with-18, unknown=12
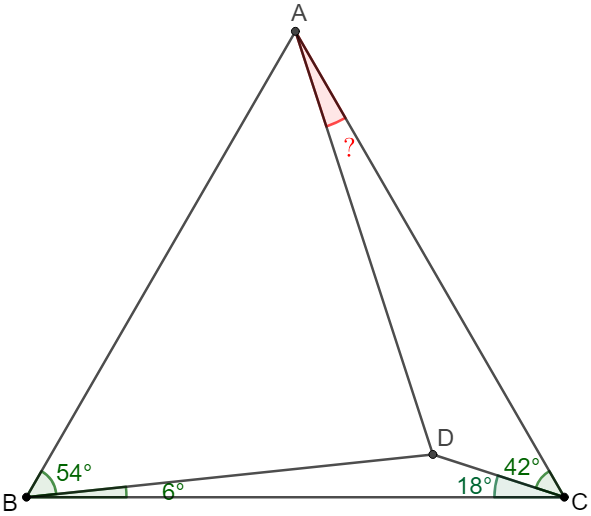
Solve:
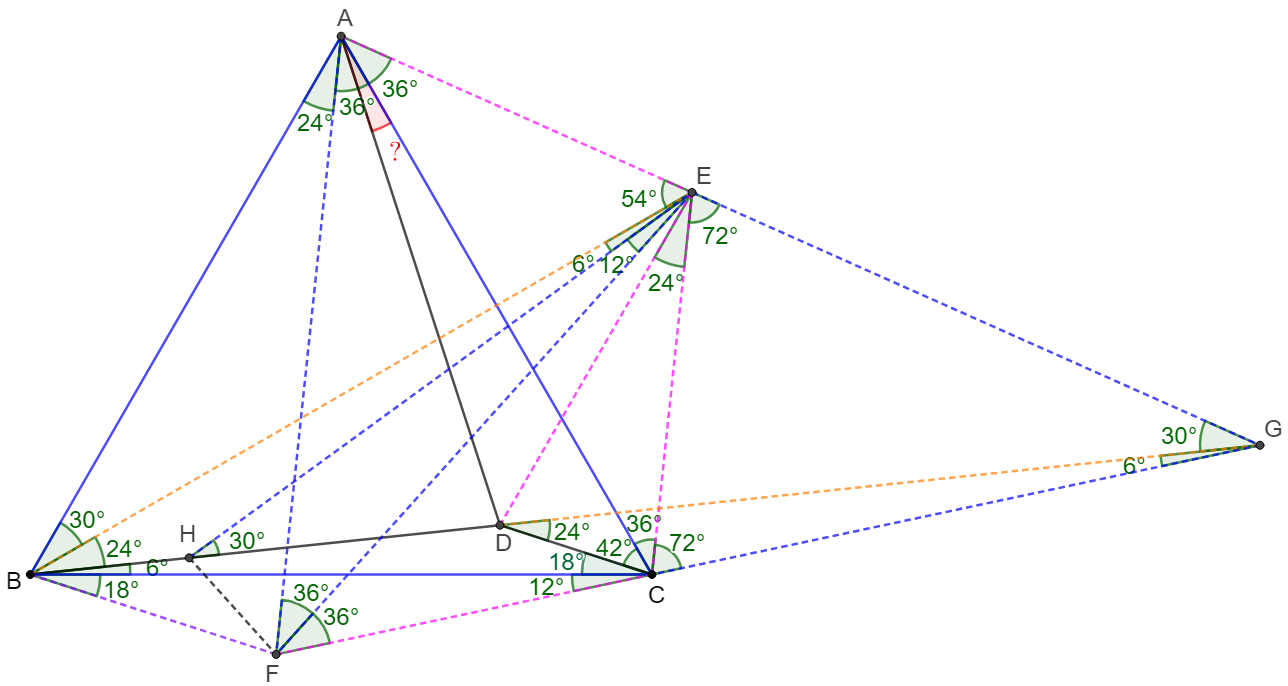 \(\begin{multline}
\shoveleft \text{Make }E \text{ outside of }\triangle{ABC} \text{ such that }\angle{EAC}=\angle{ECA}=36^{\circ}\\
\shoveleft \implies AE=CE, \angle{AEC}=108^{\circ}\\
\shoveleft \text{Make }F \text{ outside of }\triangle{ABC} \text{ such that }\angle{FCB}=12^{\circ}, CE=CF\\
\shoveleft \implies \angle{ECF}=60^{\circ}+36^{\circ}+12^{\circ}=108^{\circ}\implies \triangle{AEC}\cong\triangle{ECF}\\
\shoveleft \implies AC=EF, \angle{CFE}=\angle{CEF}=36^{\circ}=\angle{EAC}\\
\shoveleft \implies AECF \text{ is cyclic }\implies \angle{FAC}=\angle{AFE}=36^{\circ}\\
\shoveleft \implies
\begin{cases}
\angle{BAF}=60^{\circ}-36^{\circ}=24^{\circ}\\
\angle{AFC}=72^{\circ}=\angle{ACF}\implies AF=AC=AB
\end{cases}\\
\shoveleft \implies \angle{ABF}=\angle{AFB}=78^{\circ}\implies \angle{FBC}=18^{\circ}\\
\shoveleft \text{Extend }FC, BD \text{ and let they intersect at }G \\
\shoveleft \implies \angle{BGC}=180^{\circ}-6^{\circ}-18^{\circ}-78^{\circ}-72^{\circ}=6^{\circ}=\angle{CBG}\\
\shoveleft \implies BC=CG=AC, \angle{ECG}=180^{\circ}-60^{\circ}-36^{\circ}-12^{\circ}=72^{\circ}\\
\shoveleft \implies \angle{CAG}=36^{\circ}=\angle{CAE}\implies AEG \text{ are collinear}\\
\shoveleft \implies \angle{CEG}=72^{\circ}=\angle{ECG}\implies EG=CG=BC\\
\shoveleft \text{Make }H \text{ on }BD \text{ such that }\angle{BEH}=6^{\circ}=\angle{CGD}\implies \angle{EHG}=30^{\circ}=\angle{EGH}\\
\shoveleft \implies EH=EG=CG \implies \triangle{BEH}\cong\triangle{DGC}\implies BE=DG\\
\shoveleft \implies \triangle{BCE}\cong \triangle{DEG}\implies CE=DE\implies \angle{CED}=24^{\circ}\\
\shoveleft \implies \angle{AED}=180^{\circ}-72^{\circ}-24^{\circ}=84^{\circ}=2\angle{ACD}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ACD}\implies \angle{CAD}=\dfrac{\angle{CED}}{2}=\bbox[5px, border: 1px solid black]{12^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }E \text{ outside of }\triangle{ABC} \text{ such that }\angle{EAC}=\angle{ECA}=36^{\circ}\\
\shoveleft \implies AE=CE, \angle{AEC}=108^{\circ}\\
\shoveleft \text{Make }F \text{ outside of }\triangle{ABC} \text{ such that }\angle{FCB}=12^{\circ}, CE=CF\\
\shoveleft \implies \angle{ECF}=60^{\circ}+36^{\circ}+12^{\circ}=108^{\circ}\implies \triangle{AEC}\cong\triangle{ECF}\\
\shoveleft \implies AC=EF, \angle{CFE}=\angle{CEF}=36^{\circ}=\angle{EAC}\\
\shoveleft \implies AECF \text{ is cyclic }\implies \angle{FAC}=\angle{AFE}=36^{\circ}\\
\shoveleft \implies
\begin{cases}
\angle{BAF}=60^{\circ}-36^{\circ}=24^{\circ}\\
\angle{AFC}=72^{\circ}=\angle{ACF}\implies AF=AC=AB
\end{cases}\\
\shoveleft \implies \angle{ABF}=\angle{AFB}=78^{\circ}\implies \angle{FBC}=18^{\circ}\\
\shoveleft \text{Extend }FC, BD \text{ and let they intersect at }G \\
\shoveleft \implies \angle{BGC}=180^{\circ}-6^{\circ}-18^{\circ}-78^{\circ}-72^{\circ}=6^{\circ}=\angle{CBG}\\
\shoveleft \implies BC=CG=AC, \angle{ECG}=180^{\circ}-60^{\circ}-36^{\circ}-12^{\circ}=72^{\circ}\\
\shoveleft \implies \angle{CAG}=36^{\circ}=\angle{CAE}\implies AEG \text{ are collinear}\\
\shoveleft \implies \angle{CEG}=72^{\circ}=\angle{ECG}\implies EG=CG=BC\\
\shoveleft \text{Make }H \text{ on }BD \text{ such that }\angle{BEH}=6^{\circ}=\angle{CGD}\implies \angle{EHG}=30^{\circ}=\angle{EGH}\\
\shoveleft \implies EH=EG=CG \implies \triangle{BEH}\cong\triangle{DGC}\implies BE=DG\\
\shoveleft \implies \triangle{BCE}\cong \triangle{DEG}\implies CE=DE\implies \angle{CED}=24^{\circ}\\
\shoveleft \implies \angle{AED}=180^{\circ}-72^{\circ}-24^{\circ}=84^{\circ}=2\angle{ACD}\\
\shoveleft \implies E \text{ is the circumcenter of }\triangle{ACD}\implies \angle{CAD}=\dfrac{\angle{CED}}{2}=\bbox[5px, border: 1px solid black]{12^{\circ}}
\end{multline}\)
(6) 6-with-18: unknown=18
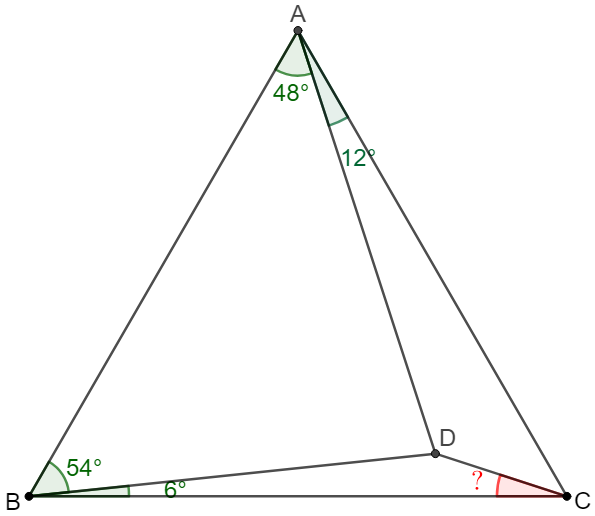
Solve:
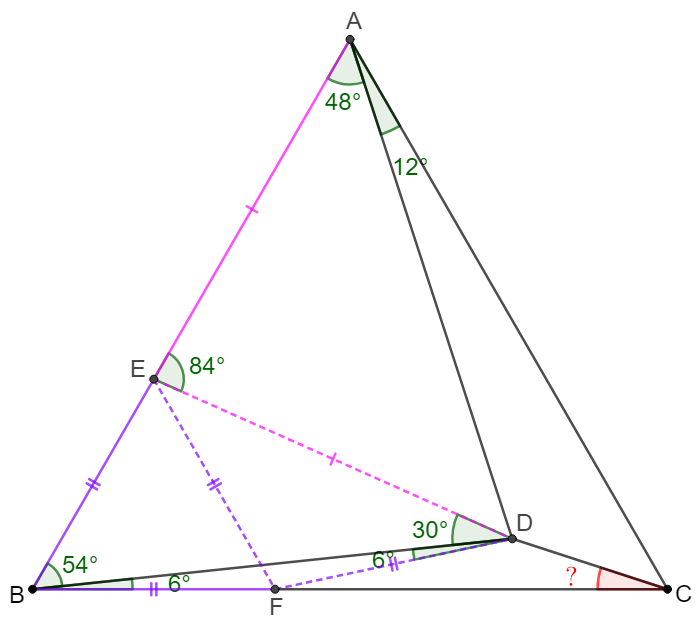 \(\begin{multline}
\shoveleft \text{Let }E \text{ on }AB \text{ such that }DE=AE\implies \angle{ADE}=\angle{DAE}=48^{\circ}\\
\shoveleft \implies \angle{BDE}=180^{\circ}-54^{\circ}-48^{\circ}-48^{\circ}=30^{\circ}\\
\shoveleft \text{Let }F \text{ on } BC \text{ such that }EF\parallel AC \implies \triangle{BEF} \text{ is equilateral}\\
\shoveleft \implies BF=EF, \angle{BFE}=60^{\circ}=2\angle{BDE} \\
\shoveleft \implies F \text{ is the circumcenter of }\triangle{BDE} \implies DF=EF\\
\shoveleft \implies \angle{FDE}=\angle{FED}=180^{\circ}-84^{\circ}-60^{\circ}=36^{\circ}\\
\shoveleft \implies \angle{BDF}=36^{\circ}-30^{\circ}=6^{\circ}\implies \angle{CFD}=12^{\circ}\\
\shoveleft \implies \angle{BCD}=30^{\circ}-12^{\circ}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }E \text{ on }AB \text{ such that }DE=AE\implies \angle{ADE}=\angle{DAE}=48^{\circ}\\
\shoveleft \implies \angle{BDE}=180^{\circ}-54^{\circ}-48^{\circ}-48^{\circ}=30^{\circ}\\
\shoveleft \text{Let }F \text{ on } BC \text{ such that }EF\parallel AC \implies \triangle{BEF} \text{ is equilateral}\\
\shoveleft \implies BF=EF, \angle{BFE}=60^{\circ}=2\angle{BDE} \\
\shoveleft \implies F \text{ is the circumcenter of }\triangle{BDE} \implies DF=EF\\
\shoveleft \implies \angle{FDE}=\angle{FED}=180^{\circ}-84^{\circ}-60^{\circ}=36^{\circ}\\
\shoveleft \implies \angle{BDF}=36^{\circ}-30^{\circ}=6^{\circ}\implies \angle{CFD}=12^{\circ}\\
\shoveleft \implies \angle{BCD}=30^{\circ}-12^{\circ}=\bbox[5px, border: 1px solid black]{18^{\circ}}
\end{multline}\)
Notes: \(\begin{multline} \shoveleft \text{Let's define symbol as following}:\\ \shoveleft \boxed{ 1}=sin6^{\circ}, \boxed{\kern 0em 2 }=sin12^{\circ},\boxed{\kern 0em 3 }=sin18^{\circ}...\\ \shoveleft \text{Applying Ceva's Theorem and some formulas like }sin(x)\cdot sin(60-x) \cdot sin(60+x)=\dfrac{sin3x}{4}\\ \shoveleft \text{Here are some facts I know from previous problems:}\\ \shoveleft \boxed{x}=\boxed{30-x}\\ \shoveleft \boxed{\color{red}3}=\dfrac{\sqrt{5}-1}{4}\\ \shoveleft \boxed{\color{red}5}=\dfrac{1}{2}\\ \shoveleft \boxed{\color{red}6}=\dfrac{\sqrt{10-2\sqrt{5}}}{4}\\ \shoveleft \boxed{\color{red}9}=\dfrac{\sqrt{5}+1}{4}\\ \shoveleft \boxed{\color{red}{10}}=\dfrac{\sqrt{3}}{2}\\ \shoveleft \boxed{\color{red}{12}}=\dfrac{\sqrt{10+2\sqrt{5}}}{4}\\ \shoveleft \boxed{\color{red}{15}}=1\\ \shoveleft 2\boxed{\color{red}3}\boxed{\color{red}{12}}=\boxed{\color{red}6}\\ \shoveleft \boxed{\color{red}{12}}=2\boxed{\color{red}6}\boxed{\color{red}9}\\ \shoveleft \boxed{1}\boxed{7}\boxed{8} = \boxed{2}\boxed{\color{red}3}\boxed{\color{red}9} \implies \dfrac{\boxed{1}\boxed{7}\boxed{8}}{\boxed{2}}=\dfrac{1}{4}\implies \dfrac{\boxed{7}\boxed{8}}{\boxed{14}}=\dfrac{1}{8}\\ \shoveleft \boxed{\color{red}3}\boxed{4}\boxed{14}=\dfrac{1}{8} \implies \boxed{4}\boxed{14}= \dfrac{\sqrt{5}+1}{8}\\ \shoveleft \begin{cases} \boxed{ 1}\boxed{\color{red}5}\boxed{\color{red}{12}} = \boxed{2}\boxed{4}\boxed{\color{red}6}\\ \boxed{ 1}\boxed{\color{red}6}\boxed{7} = \boxed{\kern0em 2}\boxed{2}\boxed{\color{red}{12}} \end{cases} \implies \dfrac{\boxed{2} \boxed{\color{red}5}}{\boxed{4}\boxed{7}}=\dfrac{3-\sqrt{5}}{2} \implies \dfrac{\boxed{2}}{\boxed{ 4}\boxed{ 7}}=3-\sqrt{5}\\ \shoveleft \boxed{1}\boxed{\color{red}9}\boxed{11}=\dfrac{\boxed{\color{red}3}}{4} \implies \boxed{1}\boxed{11}=\dfrac{3-\sqrt{5}}{8}\\ \shoveleft \boxed{2}\boxed{8}\boxed{\color{red}{12}}=\dfrac{\boxed{\color{red}6}}{4} \implies \boxed{2}\boxed{8}=\dfrac{\sqrt{5}-1}{8}\\ \shoveleft \boxed{\color{red}3}\boxed{7}\boxed{13}=\dfrac{\boxed{\color{red}9}}{4} \implies \boxed{7}\boxed{13}=\dfrac{3+\sqrt{5}}{8} \implies \boxed{1}\boxed{7}\boxed{11}\boxed{13}=\dfrac{1}{16}\\ \shoveleft \boxed{4}\boxed{\color{red}6}\boxed{14}=\dfrac{\boxed{\color{red}{12}}}{4} \implies \boxed{4}\boxed{14}=\dfrac{\sqrt{5}+1}{2}=\dfrac{\boxed{1}\boxed{7}}{\boxed{2}\boxed{2}}\implies \boxed{1}\boxed{14}=2\boxed{2}\\ \end{multline}\)
05/27/2024
$DEFG$ is a square inscribed in $\triangle{ABC}$ such that $D,E,G$ are on side $BC,CA,AB$ respectively, and $AG=7, GB=6, BD=DC, CE=2, EA=9$. Find the area of $ABCD$, $[ABCD]$
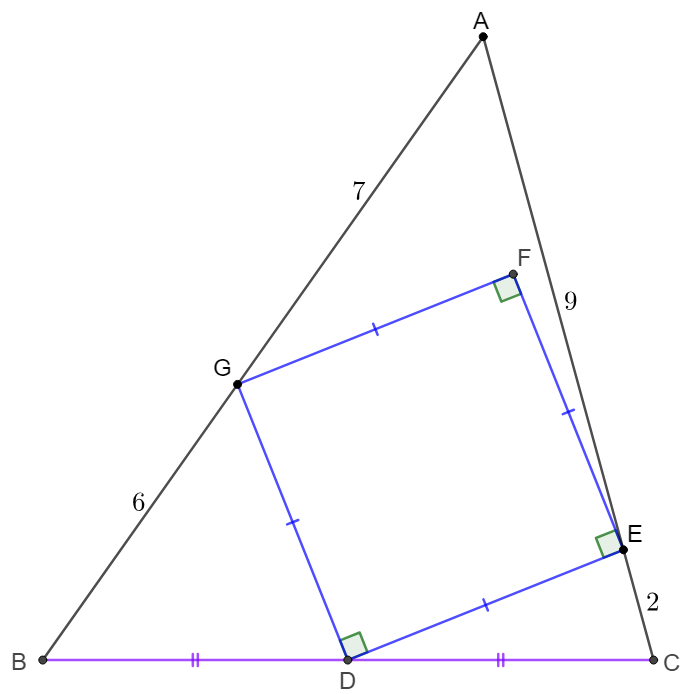
Solve:
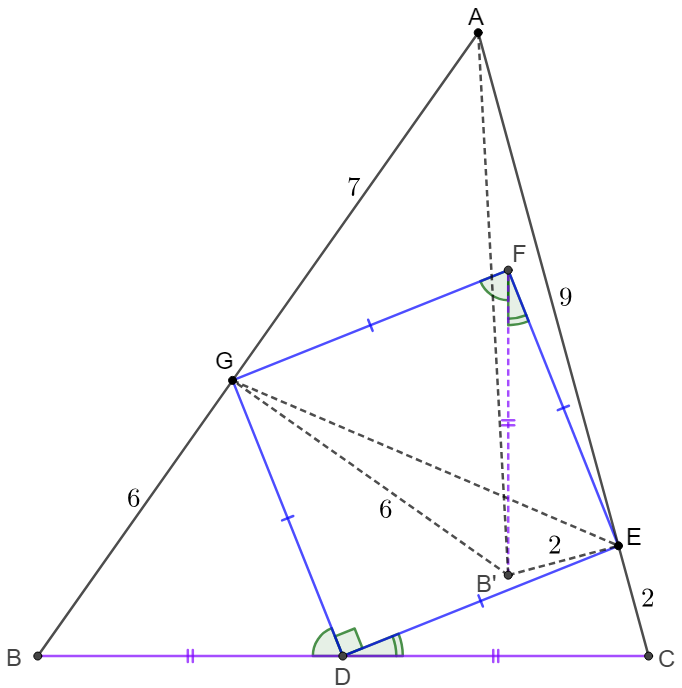 \(\begin{multline}
\shoveleft \text{Make }B' \text{ inside }ABCD \text{ such that }B'F=BD=CD, \angle{BDG}=\angle{B'FG} \implies \\
\shoveleft \angle{CDE}=90^{\circ}-\angle{BDG}=\angle{B'FE}\implies \triangle{BDG}\cong\triangle{B'FG, \triangle{CDE}\cong\triangle{B'FE}}\\
\shoveleft \implies
\begin{cases}
\angle{BGD}=\angle{B'GF} \implies \angle{BGD}+\angle{B'GD}=\angle{B'GF}+\angle{B'GD}=90^{\circ}\\
\angle{CED}=\angle{B'EF} \implies \angle{CED}+\angle{B'ED}=\angle{B'EF}+\angle{B'ED}=90^{\circ}\\
\end{cases}\\
\shoveleft \implies B'G \perp AG, B'E \perp AE\implies AB'=\sqrt{49+36}=\sqrt{85}, AEB'G \text{ is cyclic }\\
\shoveleft \text{By Ptolemy Theorem of Cyclic Quadrilateral, we know that }\\
\shoveleft AG \cdot B'E+B'G\cdot AE=AB' \cdot GE \implies GE=\dfrac{14+54}{\sqrt{85}}=\dfrac{68}{\sqrt{85}}\\
\shoveleft \implies [DEFG]=\dfrac{GE^2}{2}=\dfrac{68^2}{2*85}=\bbox[5px, border: 1px solid black]{\dfrac{136}{5}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }B' \text{ inside }ABCD \text{ such that }B'F=BD=CD, \angle{BDG}=\angle{B'FG} \implies \\
\shoveleft \angle{CDE}=90^{\circ}-\angle{BDG}=\angle{B'FE}\implies \triangle{BDG}\cong\triangle{B'FG, \triangle{CDE}\cong\triangle{B'FE}}\\
\shoveleft \implies
\begin{cases}
\angle{BGD}=\angle{B'GF} \implies \angle{BGD}+\angle{B'GD}=\angle{B'GF}+\angle{B'GD}=90^{\circ}\\
\angle{CED}=\angle{B'EF} \implies \angle{CED}+\angle{B'ED}=\angle{B'EF}+\angle{B'ED}=90^{\circ}\\
\end{cases}\\
\shoveleft \implies B'G \perp AG, B'E \perp AE\implies AB'=\sqrt{49+36}=\sqrt{85}, AEB'G \text{ is cyclic }\\
\shoveleft \text{By Ptolemy Theorem of Cyclic Quadrilateral, we know that }\\
\shoveleft AG \cdot B'E+B'G\cdot AE=AB' \cdot GE \implies GE=\dfrac{14+54}{\sqrt{85}}=\dfrac{68}{\sqrt{85}}\\
\shoveleft \implies [DEFG]=\dfrac{GE^2}{2}=\dfrac{68^2}{2*85}=\bbox[5px, border: 1px solid black]{\dfrac{136}{5}}
\end{multline}\)