04/05/2024

$AD$ is the height of right angle triangle $\triangle{ABC}$,

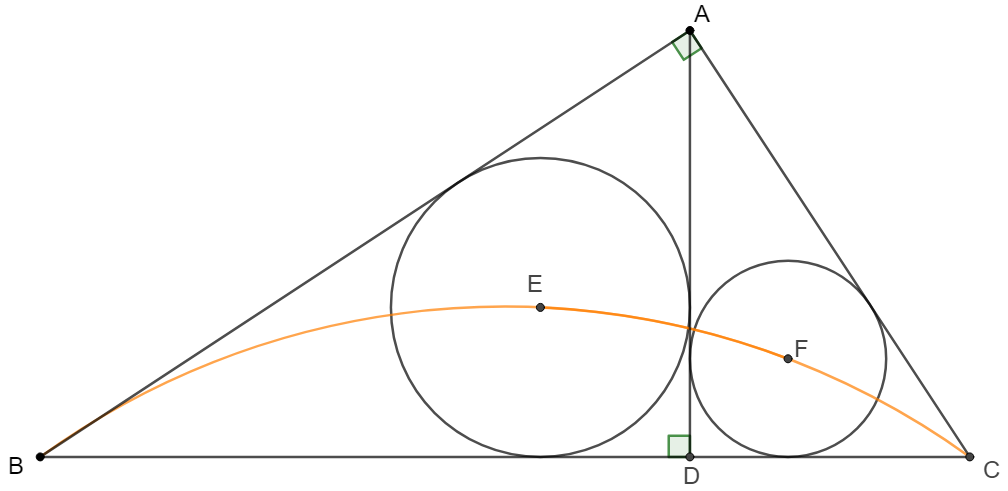
Prove:

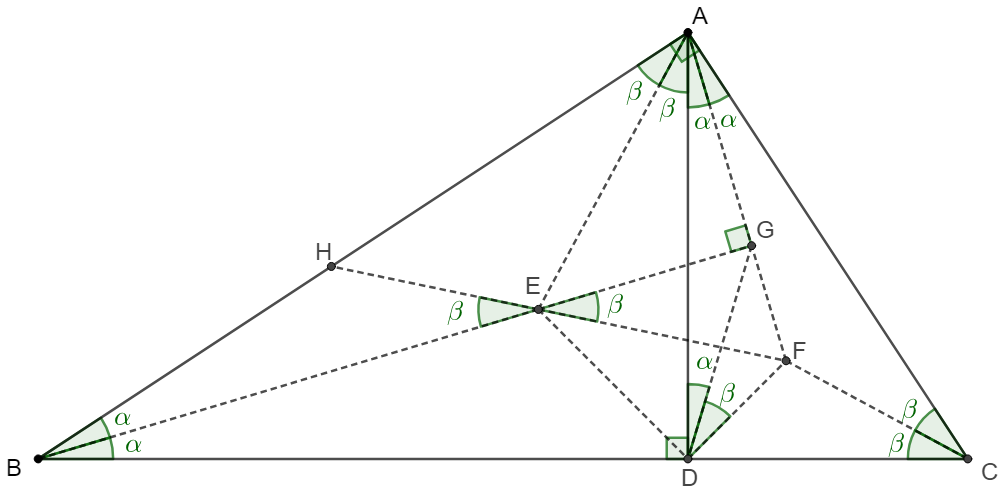\(\begin{multline} \shoveleft \text{Connect }AE, AF, BE, CF, DE, DF, \text{extend }FE, BE \\ \shoveleft \text{ and intersect } AB, AF \text{ at } H, G \text{ respectively.}\\ \shoveleft \text{Let }\angle{ABE}=\alpha, \angle{ACF}=\beta \implies \alpha + \beta=45^{\circ}\\ \shoveleft \implies \angle{CBE}=\angle{CAG}=\angle{DAG}=\alpha\\ \shoveleft \angle{BCF}=\angle{BAE}=\angle{DAE}=\beta\\ \shoveleft \implies \text{(1) } ABDG \text{ is cyclic }\implies \angle{ADG}=\angle{ABE}=\alpha\\ \shoveleft \angle{ADF}=45^{\circ}\implies \angle{FDG}=\beta\\ \shoveleft \implies \text{(2) } \angle{AGB}=90^{\circ}=\angle{ADB}\implies DEGF \text{ is cyclic}\\ \shoveleft \implies \angle{FEG}=\angle{FDG}=\beta \implies \angle{BEH}=\beta=\angle{ACF}\\ \shoveleft \implies BEFC \text{ is cyclic} \blacksquare \end{multline}\)