03/23/2024
Suppose $T$ is the circumcenter of $\triangle{ABC}$, and $A$ is the center of another circle which intersects with $\odot{T}$ at $D,E$. $CD\cap BE=K$ and $K$ is on $\odot{A}$. Prove that $AK \cdot BC = AT \cdot DE$.
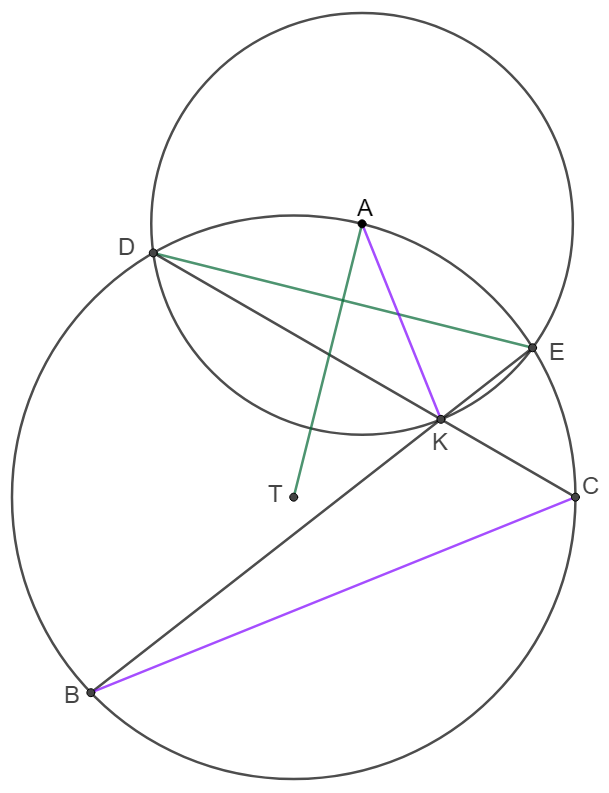
Prove:
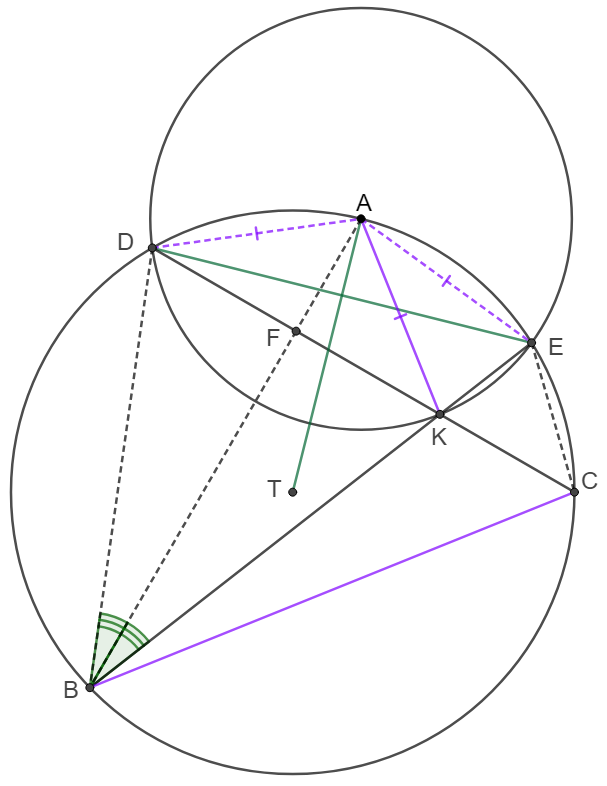 \(\begin{multline}
\shoveleft \text{Connect }AB, AD, AE, \text{let }AB\cap CD=F\\
\shoveleft \implies AD=AE=AK \implies \angle{AEK}=\angle{AKE},\angle{ABD}=\angle{ABE}\\
\shoveleft \implies 180^{\circ}-\angle{AEK}=180^{\circ}-\angle{AKE} \implies \angle{AKB}=\angle{ADB}\\
\shoveleft \implies \angle{DAB}=\angle{KAB}\implies \triangle{ADB}\cong\triangle{AKB}\implies BD=BK\\
\shoveleft \implies \angle{BDK}=\angle{BKD}\implies \angle{BTC}=2\angle{BDK}=2(180^{\circ}-\angle{DKE})=\angle{DAE}\\
\shoveleft \implies \triangle{DAE}\sim\triangle{BTC}\implies \dfrac{AD}{DE}=\dfrac{BT}{BC}\implies \dfrac{AK}{DE}=\dfrac{AT}{BC}\implies AK \cdot BC=AT\cdot DE\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Connect }AB, AD, AE, \text{let }AB\cap CD=F\\
\shoveleft \implies AD=AE=AK \implies \angle{AEK}=\angle{AKE},\angle{ABD}=\angle{ABE}\\
\shoveleft \implies 180^{\circ}-\angle{AEK}=180^{\circ}-\angle{AKE} \implies \angle{AKB}=\angle{ADB}\\
\shoveleft \implies \angle{DAB}=\angle{KAB}\implies \triangle{ADB}\cong\triangle{AKB}\implies BD=BK\\
\shoveleft \implies \angle{BDK}=\angle{BKD}\implies \angle{BTC}=2\angle{BDK}=2(180^{\circ}-\angle{DKE})=\angle{DAE}\\
\shoveleft \implies \triangle{DAE}\sim\triangle{BTC}\implies \dfrac{AD}{DE}=\dfrac{BT}{BC}\implies \dfrac{AK}{DE}=\dfrac{AT}{BC}\implies AK \cdot BC=AT\cdot DE\blacksquare
\end{multline}\)
02/24/2024
$AB$ is the diameter of semicircle $\odot{O}$ and $C, E$ are two points on semicircle. $CD\perp AB, EF \perp AB, EG \perp CO$, show that $CD=FG$
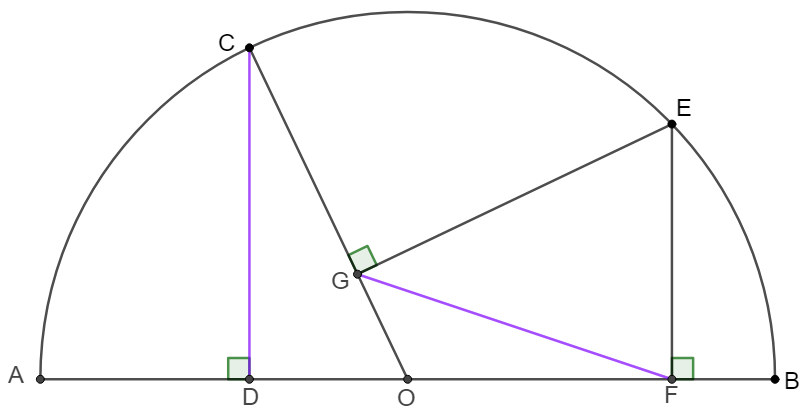
Prove 1:
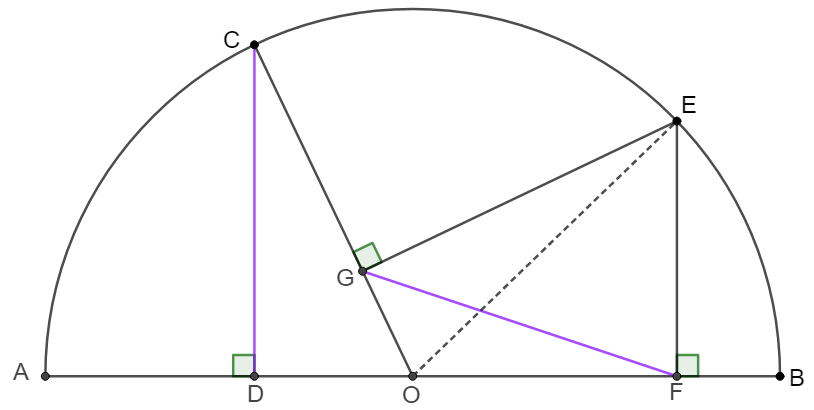 \(\begin{multline}
\shoveleft \text{Connect }EO, \text{easy to see} EFOG \text{ is cyclic }\implies \angle{COD}=\angle{FEG}\\
\shoveleft \text{Let }AO=CO=EO=R \implies CD=R\cdot sin\angle{COD}\\
\shoveleft = R\cdot sin(\angle{GEO}+\angle{FEO})\\
\shoveleft =R \cdot(sin{\angle{GEO}}\cdot cos{\angle{FEO}}+cos{\angle{GEO}} \cdot sin{\angle{FEO}})\\
\shoveleft =R \cdot (\dfrac{GO}{R}\dfrac{EF}{R}+\dfrac{GE}{R} \cdot \dfrac{OF}{R})=\dfrac{GO \cdot EF + GE \cdot OF }{R}\\
\shoveleft \text{Ptolemy's theorem} \implies GO \cdot EF + GE \cdot OF = GF \cdot R\\
\shoveleft \implies CD = R \cdot sin{\angle{COD}}=GF \blacksquare\\
\end{multline}\)
Prove 2:
\(\begin{multline}
\shoveleft \text{Connect }EO, \text{easy to see} EFOG \text{ is cyclic }\implies \angle{COD}=\angle{FEG}\\
\shoveleft \text{Let }AO=CO=EO=R \implies CD=R\cdot sin\angle{COD}\\
\shoveleft = R\cdot sin(\angle{GEO}+\angle{FEO})\\
\shoveleft =R \cdot(sin{\angle{GEO}}\cdot cos{\angle{FEO}}+cos{\angle{GEO}} \cdot sin{\angle{FEO}})\\
\shoveleft =R \cdot (\dfrac{GO}{R}\dfrac{EF}{R}+\dfrac{GE}{R} \cdot \dfrac{OF}{R})=\dfrac{GO \cdot EF + GE \cdot OF }{R}\\
\shoveleft \text{Ptolemy's theorem} \implies GO \cdot EF + GE \cdot OF = GF \cdot R\\
\shoveleft \implies CD = R \cdot sin{\angle{COD}}=GF \blacksquare\\
\end{multline}\)
Prove 2:
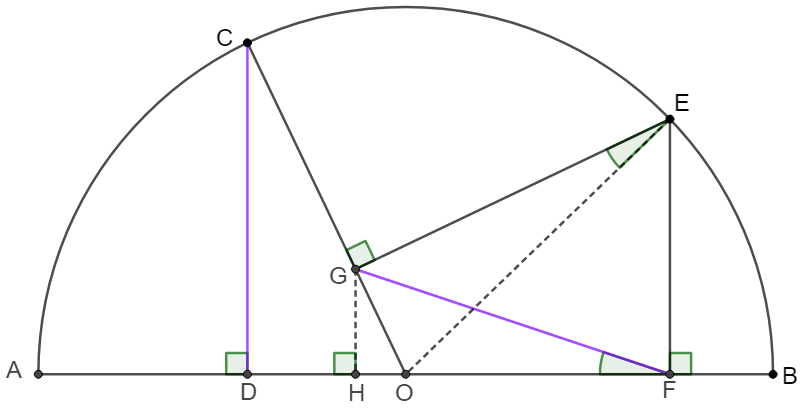 \(\begin{multline}
\shoveleft \text{Make }GH \perp AB \text{ at }H \implies \triangle{GOH}\sim \triangle{COD}\implies \dfrac{GO}{GH}=\dfrac{CO}{CD}\\
\shoveleft EFOG \text{ is cyclic }\implies \angle{GFO}=\angle{GEO}\implies \triangle{GEO}\sim\triangle{GFH}\\
\shoveleft \implies \dfrac{GO}{GH}=\dfrac{EO}{FG}=\dfrac{CO}{FG}=\dfrac{CO}{CD}\implies CD=FG\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Make }GH \perp AB \text{ at }H \implies \triangle{GOH}\sim \triangle{COD}\implies \dfrac{GO}{GH}=\dfrac{CO}{CD}\\
\shoveleft EFOG \text{ is cyclic }\implies \angle{GFO}=\angle{GEO}\implies \triangle{GEO}\sim\triangle{GFH}\\
\shoveleft \implies \dfrac{GO}{GH}=\dfrac{EO}{FG}=\dfrac{CO}{FG}=\dfrac{CO}{CD}\implies CD=FG\blacksquare
\end{multline}\)
03/25/2024
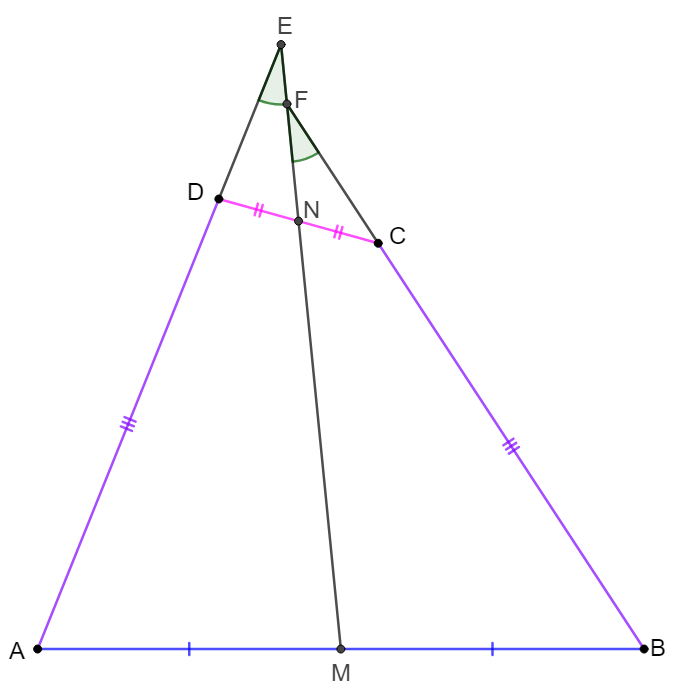
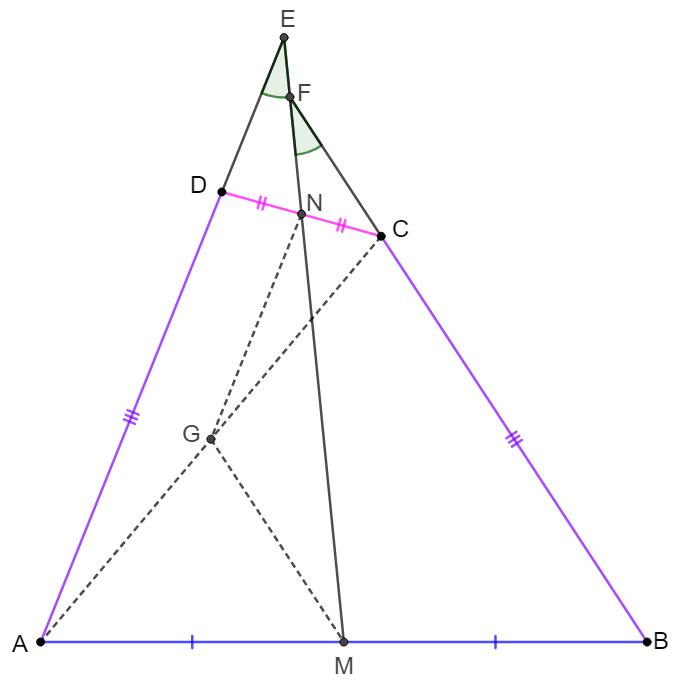
$AD=BC$ in quadrilateral $ABCD$ and $M,N$ are midpoints of sides $AB, CD$ . Extended $AD, MN$ intersect at $E$. Extended $BC, MN$ intersect at $F$. Prove $\angle{DEN}=\angle{CFN}$
Prove:
 \(\begin{multline}
\shoveleft \text{Connect } BD \text{ and make }G \text{ on } BD \text{ such that }MG\parallel AD \\
\shoveleft AM=MB \implies BG=GD, GM=\dfrac{AD}{2}, \angle{DEN}=\angle{GMN}\\
\shoveleft \implies GN \parallel BC, GN=\dfrac{BC}{2}=\dfrac{AD}{2}=GM\\
\shoveleft \implies \angle{GMN}=\angle{GNM}, \angle{CFN}=\angle{GNM}\\
\shoveleft \implies \angle{DEN}=\angle{GMN}=\angle{CFN}\blacksquare
\end{multline}\)
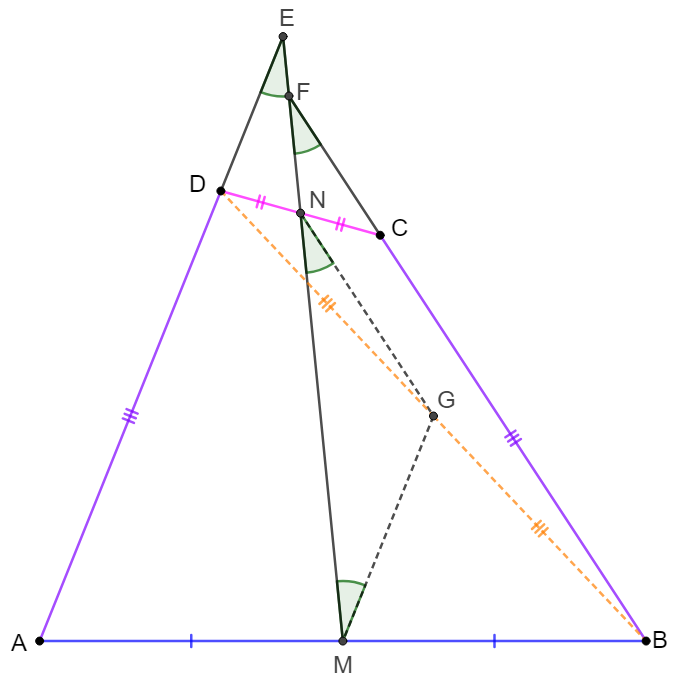
Note: Connect $AC$ will be similar:
\(\begin{multline}
\shoveleft \text{Connect } BD \text{ and make }G \text{ on } BD \text{ such that }MG\parallel AD \\
\shoveleft AM=MB \implies BG=GD, GM=\dfrac{AD}{2}, \angle{DEN}=\angle{GMN}\\
\shoveleft \implies GN \parallel BC, GN=\dfrac{BC}{2}=\dfrac{AD}{2}=GM\\
\shoveleft \implies \angle{GMN}=\angle{GNM}, \angle{CFN}=\angle{GNM}\\
\shoveleft \implies \angle{DEN}=\angle{GMN}=\angle{CFN}\blacksquare
\end{multline}\)
Note: Connect $AC$ will be similar:
03/26/2024
$x,y,z$ are real numbers satisfying $x+y+z=2024, \dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{2024}$, find $(x-2024)(y-2024)(z-2024)$.
Solve 1: \(\begin{multline} \shoveleft \text{Suppose }xyz=2024k \implies zy+yz+zx=k\\ \shoveleft \implies x,y,z \text{ are roots of equation }t^3-2024t^2+kt-2024k=0\\ \shoveleft \implies (t-2024)(t^2+k)=0 \implies \text{one of }x,y,z \text{ equals to } 2024\\ \shoveleft \implies (x-2024)(y-2024)(z-2024)=\bbox[5px, border: 1px solid black]{0} \end{multline}\) Solve 2: \(\begin{multline} \shoveleft \text{Let }x=bty, z=by \implies (x+y+z)(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z})\\ \shoveleft =1+bt+t+1+b+\dfrac{1}{t}+1+\dfrac{1}{bt}+\dfrac{1}{b}=1\\ \shoveleft \implies t(t+1)b^2+(t^2+2t+1)b+(t+1)=0\\ \shoveleft \implies (t+1)(tb+1)(b+1)=0\\ \shoveleft \text{Case 1: }t=-1 \implies x+z=0 \implies y=2024\\ \shoveleft \text{Case 2: }t=-\dfrac{1}{b} \implies x=-y \implies z=2024\\ \shoveleft \text{Case 3: }b=-1 \implies z=-y \implies x=2024\\ \shoveleft \implies (x-2024)(y-2024)(z-2024)=\bbox[5px, border: 1px solid black]{0} \end{multline}\)
03/27/2024
$ABCD$ is a cyclic quadrilateral with $AB=7, CD=8$. Points $P, Q$ are on $AB$ such that $AP=BQ=3$ . Points $R, S$ are on $CD$ such that $CR=DS=2$. Prove that $PQRS$ is cyclic.
Prove: \(\begin{multline} \shoveleft \text{If }AB \parallel CD, \text{it is easy to see that }PQRS \text{ is cyclic}.\\ \shoveleft \text{Suppose }AB\cap CD=E. \text{Without loss of generality, suppose}\\ \shoveleft EA=a, ED=b, \text{By power of point} \implies EA \cdot EB = ED \cdot EC\\ \shoveleft \implies a(a+7)=b(b+8) \implies a^2+7a=b^2+8b\\ \shoveleft \implies EP\cdot EQ = (a+3)(a+4)=a^2+7a+12=b^2+8b+12\\ \shoveleft =(b+2)(b+6) = ES \cdot ER \implies PQRS \text{ is cyclic}\blacksquare \end{multline}\)