02/12/2024
Points $D,E,F$ are on side $BC, CA, AB$ of acute triangle $\triangle{ABC}$ respectively such that $DE \perp AC, EF \perp AB, FD \perp BC$. Prove that $\tfrac{AF}{AB}+\tfrac{BD}{BC}+\tfrac{CE}{CA}=1$
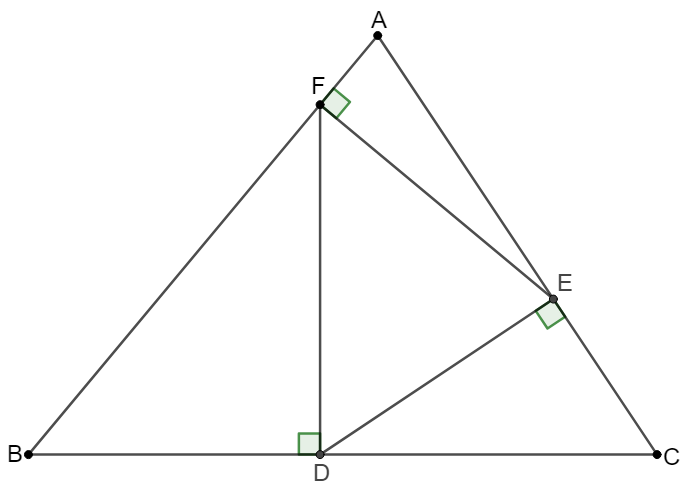
Prove 1:
 \(\begin{multline}\nonumber
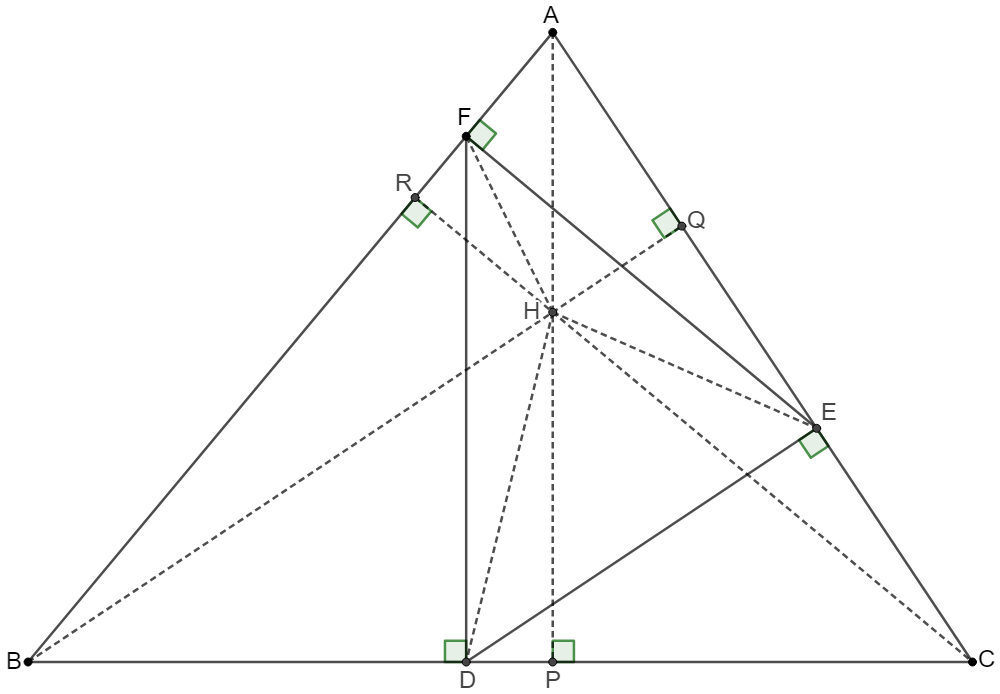
\shoveleft \text{Make }AP \perp BC \text{ at }P, BQ \perp CA \text{ at }Q, CR \perp AB \text{ at }R\\
\shoveleft AP, BQ, CR \text{ intersect at }H, \text{ connect }DH, EH, \text{ and } FH\\
\shoveleft [AFC]=[AEF]+[CEF],[CEF]=[HEF]\\
\shoveleft [ABD]=[BDF]+[ADF],[ADF]=[HDF]\\
\shoveleft [BCE]=[CDE]+[BDE],[BDE]=[HDE]\\
\shoveleft [HEF]+[HDF]+[HDE]=[DEF]\implies\\
\shoveleft [AFC]+[ABD]+[BCE]=[AEF]+[BDF]+[CDE]+[DEF]\\
\shoveleft =[ABC] \implies \dfrac{AF}{AB}+\dfrac{BD}{BC}+\dfrac{CE}{CA}\\
\shoveleft =\dfrac{AF\cdot CR}{AB \cdot CR}+\dfrac{BD \cdot AP}{BC \cdot AP}+\dfrac{CE \cdot BQ}{CA \cdot BQ}\\
\shoveleft =\dfrac{[AFC]+[ABD]+[BCE]}{[ABC]}=\dfrac{[ABC]}{[ABC]}=1\blacksquare\\
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft \text{Make }AP \perp BC \text{ at }P, BQ \perp CA \text{ at }Q, CR \perp AB \text{ at }R\\
\shoveleft AP, BQ, CR \text{ intersect at }H, \text{ connect }DH, EH, \text{ and } FH\\
\shoveleft [AFC]=[AEF]+[CEF],[CEF]=[HEF]\\
\shoveleft [ABD]=[BDF]+[ADF],[ADF]=[HDF]\\
\shoveleft [BCE]=[CDE]+[BDE],[BDE]=[HDE]\\
\shoveleft [HEF]+[HDF]+[HDE]=[DEF]\implies\\
\shoveleft [AFC]+[ABD]+[BCE]=[AEF]+[BDF]+[CDE]+[DEF]\\
\shoveleft =[ABC] \implies \dfrac{AF}{AB}+\dfrac{BD}{BC}+\dfrac{CE}{CA}\\
\shoveleft =\dfrac{AF\cdot CR}{AB \cdot CR}+\dfrac{BD \cdot AP}{BC \cdot AP}+\dfrac{CE \cdot BQ}{CA \cdot BQ}\\
\shoveleft =\dfrac{[AFC]+[ABD]+[BCE]}{[ABC]}=\dfrac{[ABC]}{[ABC]}=1\blacksquare\\
\end{multline}\)
Prove 2:
 \(\begin{multline}
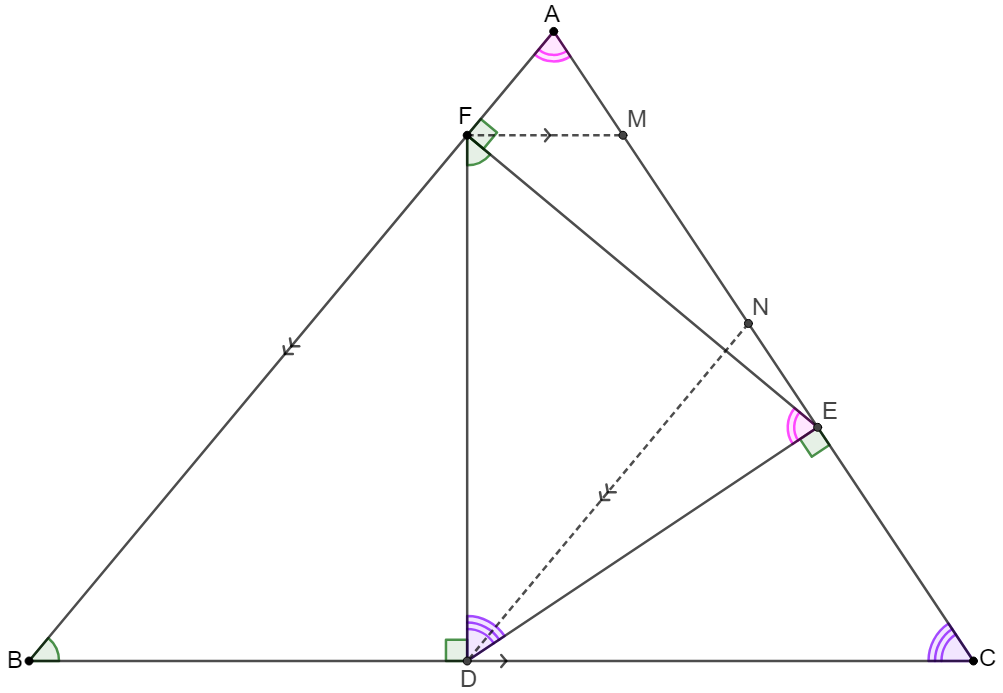
\shoveleft \text{Let }M, N \text{ on }CA \text{ such that }FM \parallel BC, DN \parallel AB\\
\shoveleft \angle{ABC}=90^{\circ}-\angle{BFD}=\angle{DFE}, \angle{BCA}=90^{\circ}-\angle{CDE}=\angle{EDF}\\
\shoveleft \implies \triangle{DEF}\sim\triangle{ABC}\implies \dfrac{DE}{EF}=\dfrac{CA}{AB}=\dfrac{AM}{AF}\\
\shoveleft DN \parallel AB, EF \perp AB \implies DN \perp EF \implies\\
\shoveleft \angle{EDN}=90^{\circ}-\angle{DEF}=\angle{AEF}\implies \triangle{AEF}\sim\triangle{NDE}\\
\shoveleft \implies \dfrac{DE}{EF}=\dfrac{NE}{AF}\implies \dfrac{NE}{AF}=\dfrac{AM}{AF}\\
\shoveleft \implies NE=AM \implies AN=ME\\
\shoveleft \implies \dfrac{AF}{AB}+\dfrac{BD}{BC}+\dfrac{CE}{CA}=\dfrac{AM}{CA}+\dfrac{AN}{CA}+\dfrac{CE}{CA}\\
\shoveleft =\dfrac{AM+ME+CE}{CA}=1\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }M, N \text{ on }CA \text{ such that }FM \parallel BC, DN \parallel AB\\
\shoveleft \angle{ABC}=90^{\circ}-\angle{BFD}=\angle{DFE}, \angle{BCA}=90^{\circ}-\angle{CDE}=\angle{EDF}\\
\shoveleft \implies \triangle{DEF}\sim\triangle{ABC}\implies \dfrac{DE}{EF}=\dfrac{CA}{AB}=\dfrac{AM}{AF}\\
\shoveleft DN \parallel AB, EF \perp AB \implies DN \perp EF \implies\\
\shoveleft \angle{EDN}=90^{\circ}-\angle{DEF}=\angle{AEF}\implies \triangle{AEF}\sim\triangle{NDE}\\
\shoveleft \implies \dfrac{DE}{EF}=\dfrac{NE}{AF}\implies \dfrac{NE}{AF}=\dfrac{AM}{AF}\\
\shoveleft \implies NE=AM \implies AN=ME\\
\shoveleft \implies \dfrac{AF}{AB}+\dfrac{BD}{BC}+\dfrac{CE}{CA}=\dfrac{AM}{CA}+\dfrac{AN}{CA}+\dfrac{CE}{CA}\\
\shoveleft =\dfrac{AM+ME+CE}{CA}=1\blacksquare
\end{multline}\)
02/14/2024
$a+\dfrac{1}{b}=x, b+\dfrac{1}{c}=y, c+\dfrac{1}{a}=z, $ find $abc$.
Solve: \(\begin{multline} \shoveleft \text{Sum up three equations }\implies a+b+c+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=x+y+z\\ \shoveleft \text{Multiple three equations }\implies abc+a+b+c+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{abc}=xyz\\ \shoveleft \implies abc+x+y+z+\dfrac{1}{abc}=xyz\implies (abc)^2+(x+y+z-xyz){abc}+1=0\\ \shoveleft \implies abc=\bbox[5px, border: 1px solid black]{\dfrac{xyz-x-y-z\pm\sqrt{(xyz-x-y-z)^2-4}}{2}} \end{multline}\)
02/15/2024
$x+\dfrac{1}{x}=3$, find $\dfrac{x^6+1}{x^5+x}$
Solve: \(\begin{multline} \shoveleft x+\dfrac{1}{x}=3 \implies x^2+\dfrac{1}{x^2}=(x+\dfrac{1}{x})^2-2=7\\ \shoveleft \implies x^3+\dfrac{1}{x^3}=(x+\dfrac{1}{x})(x^2-1+\dfrac{1}{x^2})=3*6=18\\ \shoveleft \implies \dfrac{x^6+1}{x^5+x}=\dfrac{x^3+\dfrac{1}{x^3}}{x^2+\dfrac{1}{x^2}}=\bbox[5px, border: 1px solid black]{\dfrac{18}{7}} \end{multline}\)
02/18/2024
$\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}=1$, find $\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}$
Solve: \(\begin{multline} \shoveleft (\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y})(x+y+z)\\ \shoveleft =\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}+x+y+z\\ \shoveleft \implies \dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}=\bbox[5px, border: 1px solid black]{0} \end{multline}\)
02/20/2024
$a+b+c=0, \dfrac{1}{a+1}+\dfrac{1}{b+2}+\dfrac{1}{c+3}=0$, find $(a+1)^2+(b+2)^2+(c+3)^2$
Solve: \(\begin{multline} \shoveleft \text{Let }x=a+1, y=b+2, z=c+3 \implies x+y+z=6\\ \shoveleft \dfrac{1}{a+1}+\dfrac{1}{b+2}+\dfrac{1}{c+3}=0 \implies \dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\\ \shoveleft \implies xy+yz+zx=0 \implies x^2+y^2+z^2=(x+y+z)^2\\ \shoveleft \implies x^2+y^2+z^2=(a+1)^2+(b+2)^2+(c+3)^2=\bbox[5px, border: 1px solid black]{36} \end{multline}\)
02/21/2024
$abc \neq 0, a+b+c=0$, find $\dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}$
Solve: \(\begin{multline} \shoveleft (a+b+c)^3=a^3+b^3+c^3+6abc+3[ab(a+b)+bc(b+c)+ca(c+a)]\\ \shoveleft a+b+c=0\implies (a+b+c)^3=a^3+b^3+c^3-3abc=0, abc \neq 0\\ \shoveleft \implies \dfrac{a^3+b^3+c^3}{abc}=3\implies \dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}=\bbox[5px, border: 1px solid black]{3} \end{multline}\)