01/02/2024
$AB$ and $CD$ are two tangent lines of $\odot{O}$. $AB=8, CD=5$, $AD\cap BC=E$, and $E$ is on $\odot{O}$. Find $AC$.
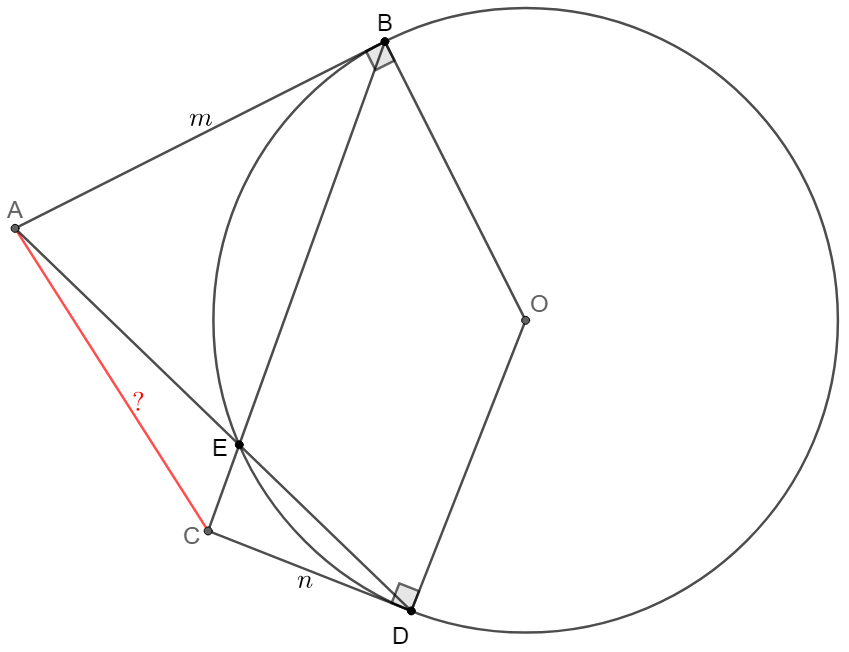
Solve 1:
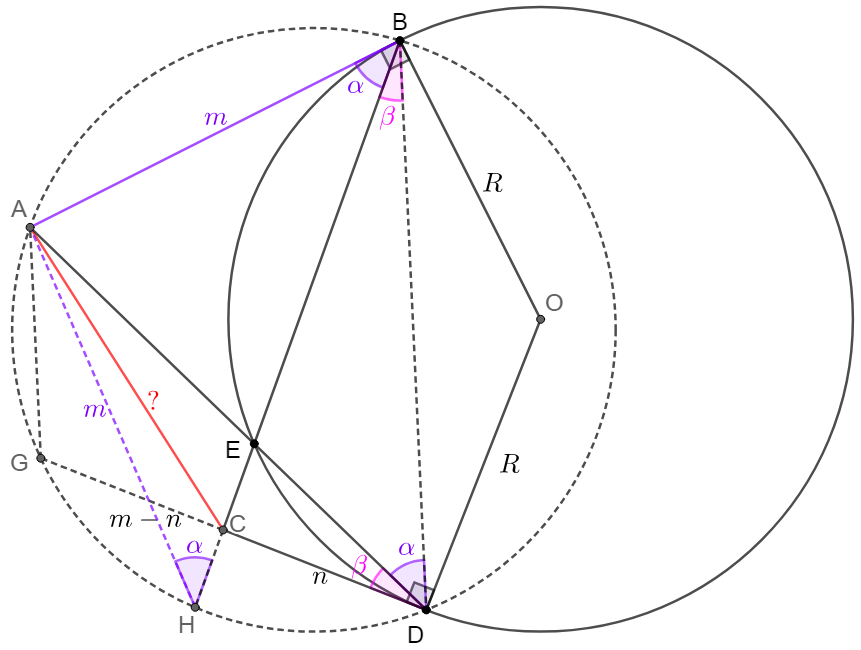 \(\begin{multline}
\shoveleft \text{WLOG, suppose }AB>CD \implies C \text{ is inside the circumcircle of }\triangle{ABD}\\
\shoveleft \text{Extend }BC, DC \text{ and intersect the circumcircle of }\triangle{ABD} \text{ at }H, G \text{ respectively}\\
\shoveleft \text{Let }AB=m, \angle{ABH}=\angle{ADB}=\angle{AHB}\implies AB=AH=m\\
\shoveleft \angle{ADG}=\angle{DBH}\implies \angle{ABD}=\angle{GDB}\implies \angle{AGD}+\angle{GDB}=180^{\circ}\\
\shoveleft \implies AG\parallel BD \implies ABDG \text{ is an isosceles trapezoid} \implies AB=GD=m \\
\shoveleft \text{Let }CD=n \implies CG=m-n,\text{applying Intersecting chords theorem:}\\
\shoveleft \implies CH\cdot BC = CD \cdot GC \implies CH \cdot BC=n(m-n)\\
\shoveleft \text{Applying Stewart's Theorem in }\triangle{ABH} \implies AC^2=\dfrac{AH^2BC+AB^2CH}{CH+BC}-CH \cdot BC\\
\shoveleft \implies AC^2=\dfrac{m^2\cdot BH}{BH}-CH \cdot BC=m^2-n(m-n)\implies AC=\sqrt{m^2-mn+n^2}\\
\shoveleft \text{When }m=8, n=5, AC=\sqrt{8^2+5^5-40}=\bbox[5px, border: 1px solid black]{7}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{WLOG, suppose }AB>CD \implies C \text{ is inside the circumcircle of }\triangle{ABD}\\
\shoveleft \text{Extend }BC, DC \text{ and intersect the circumcircle of }\triangle{ABD} \text{ at }H, G \text{ respectively}\\
\shoveleft \text{Let }AB=m, \angle{ABH}=\angle{ADB}=\angle{AHB}\implies AB=AH=m\\
\shoveleft \angle{ADG}=\angle{DBH}\implies \angle{ABD}=\angle{GDB}\implies \angle{AGD}+\angle{GDB}=180^{\circ}\\
\shoveleft \implies AG\parallel BD \implies ABDG \text{ is an isosceles trapezoid} \implies AB=GD=m \\
\shoveleft \text{Let }CD=n \implies CG=m-n,\text{applying Intersecting chords theorem:}\\
\shoveleft \implies CH\cdot BC = CD \cdot GC \implies CH \cdot BC=n(m-n)\\
\shoveleft \text{Applying Stewart's Theorem in }\triangle{ABH} \implies AC^2=\dfrac{AH^2BC+AB^2CH}{CH+BC}-CH \cdot BC\\
\shoveleft \implies AC^2=\dfrac{m^2\cdot BH}{BH}-CH \cdot BC=m^2-n(m-n)\implies AC=\sqrt{m^2-mn+n^2}\\
\shoveleft \text{When }m=8, n=5, AC=\sqrt{8^2+5^5-40}=\bbox[5px, border: 1px solid black]{7}
\end{multline}\)
Solve 2:
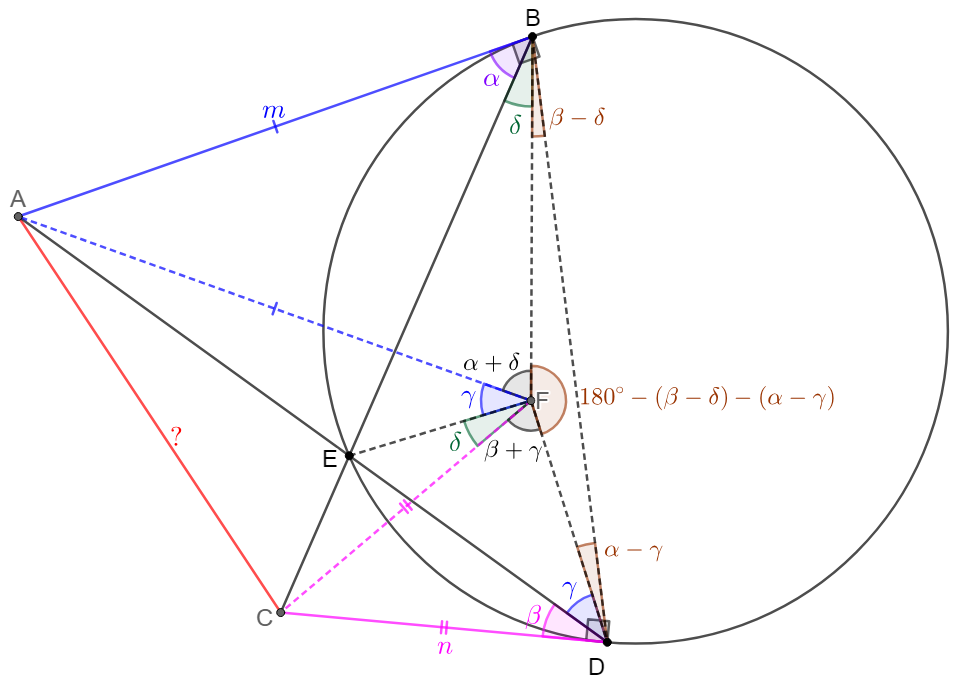 \(\begin{multline}
\shoveleft \text{Let }F \text{ be a point in the circle such that }CF=CD, AF=AB\\
\shoveleft \text{Let }\angle{ABC}=\angle{\alpha}=\angle{BDE}, \angle{ADC}=\angle{\beta}=\angle{DBE}\\
\shoveleft \text{Let }\angle{CFE}=\angle{\delta},CD=CF=CE\cdot CB \implies \angle{AFB}=\angle{\alpha}+\angle{\delta}\\
\shoveleft \implies \angle{EBF}=\angle{\delta}\implies \angle{DBF}=\angle{\beta}-\angle{\delta}\\
\shoveleft \text{Let }\angle{AFE}=\angle{\gamma},AB=AF=AE\cdot AD \implies \angle{CFD}=\angle{\beta}+\angle{\gamma}\\
\shoveleft \implies \angle{EDF}=\angle{\gamma}\implies \angle{BDF}=\angle{\alpha}-\angle{\gamma}\\
\shoveleft \implies \angle{BD}=180^{\circ}-(\angle{\beta}-\angle{\delta})-(\angle{\alpha}-\angle{4})\\
\shoveleft \implies 360^{\circ}=\angle{\delta}+\angle{\gamma}+(\angle{\alpha}+\angle{\delta})+(\angle{\beta}+\angle{\gamma})+180^{\circ}-(\angle{\beta}-\angle{\delta})-(\angle{\alpha}-\angle{\gamma})\\
\shoveleft =180^{\circ}+3(\angle{\delta}+\angle{\gamma})\implies \angle{\delta}+\angle{\gamma}=\angle{AFC}=60^{\circ}\\
\shoveleft \implies cos(\angle{AFC})=\dfrac{AF^2+CF^2-AC^2}{2AF\cdot CF}=\dfrac{1}{2}\implies AC^2=AB^2+CD^2-AB\cdot CD
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }F \text{ be a point in the circle such that }CF=CD, AF=AB\\
\shoveleft \text{Let }\angle{ABC}=\angle{\alpha}=\angle{BDE}, \angle{ADC}=\angle{\beta}=\angle{DBE}\\
\shoveleft \text{Let }\angle{CFE}=\angle{\delta},CD=CF=CE\cdot CB \implies \angle{AFB}=\angle{\alpha}+\angle{\delta}\\
\shoveleft \implies \angle{EBF}=\angle{\delta}\implies \angle{DBF}=\angle{\beta}-\angle{\delta}\\
\shoveleft \text{Let }\angle{AFE}=\angle{\gamma},AB=AF=AE\cdot AD \implies \angle{CFD}=\angle{\beta}+\angle{\gamma}\\
\shoveleft \implies \angle{EDF}=\angle{\gamma}\implies \angle{BDF}=\angle{\alpha}-\angle{\gamma}\\
\shoveleft \implies \angle{BD}=180^{\circ}-(\angle{\beta}-\angle{\delta})-(\angle{\alpha}-\angle{4})\\
\shoveleft \implies 360^{\circ}=\angle{\delta}+\angle{\gamma}+(\angle{\alpha}+\angle{\delta})+(\angle{\beta}+\angle{\gamma})+180^{\circ}-(\angle{\beta}-\angle{\delta})-(\angle{\alpha}-\angle{\gamma})\\
\shoveleft =180^{\circ}+3(\angle{\delta}+\angle{\gamma})\implies \angle{\delta}+\angle{\gamma}=\angle{AFC}=60^{\circ}\\
\shoveleft \implies cos(\angle{AFC})=\dfrac{AF^2+CF^2-AC^2}{2AF\cdot CF}=\dfrac{1}{2}\implies AC^2=AB^2+CD^2-AB\cdot CD
\end{multline}\)
Note:
- Follow above conclusion, $F$ can be proven to be the first Isodynamic Point of $\triangle{BDE}$ since $\angle{DFE}=\angle{DBE}+60^{\circ}$, $\angle{BFE}=\angle{BDE}+60^{\circ}$
- Properties of isodynamic point of a triangle:
- The first isodynamic point is the isogonal conjugate of the Fermat point of the triangle (the first isogonic center)
- The second isodynamic point is the isogonal conjugate of the second Fermat point of the triangle (the second isogonic center)
01/11/2024
$O$ is the intersection of $AD, BE$ and $CF$ in hexagon $ABCDEF$, and $S_{\triangle{ABO}}=12m^2$, $S_{\triangle{BCO}}=6m^2$, $S_{\triangle{CDO}}=8m^2$, $S_{\triangle{DEO}}=4m^2$, $S_{\triangle{EFO}}=2m^2$, find $S_{\triangle{FAO}}$
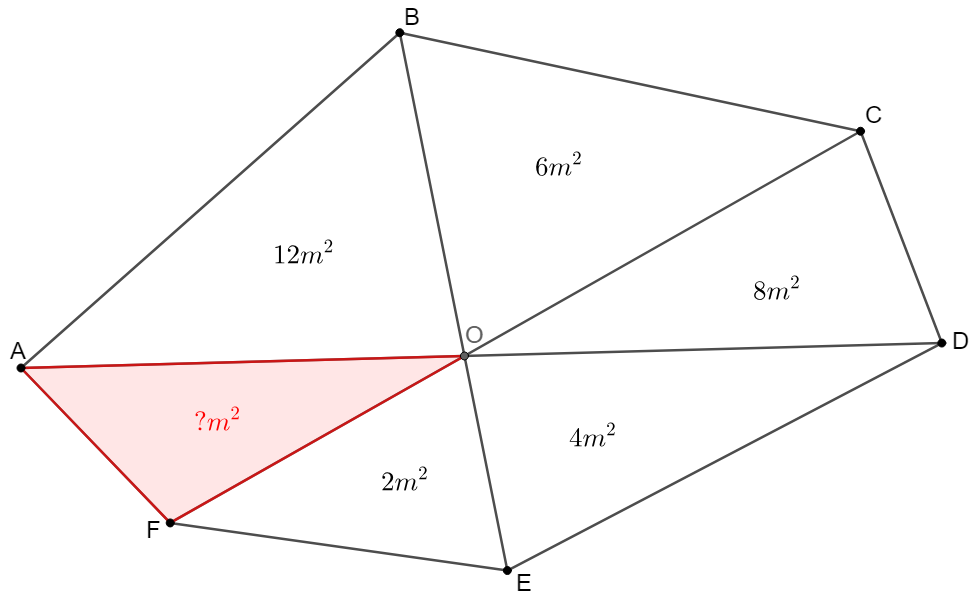 \(\begin{multline}
\shoveleft S_{\triangle{ABO}}=\dfrac{1}{2}AO\cdot BO \cdot sin{\angle{AOB}}, S_{\triangle{DEO}}=\dfrac{1}{2}DO \cdot EO \cdot sin\angle{DOE}=\dfrac{1}{2}DO \cdot EO \cdot sin\angle{AOB}\\
\shoveleft S_{\triangle{BCO}}=\dfrac{1}{2}BO\cdot CO \cdot sin{\angle{BOC}}, S_{\triangle{EFO}}=\dfrac{1}{2}EO \cdot FO \cdot sin\angle{EOF}=\dfrac{1}{2}EO \cdot FO \cdot sin\angle{BOC}\\
\shoveleft S_{\triangle{CDO}}=\dfrac{1}{2}CO\cdot DO \cdot sin{\angle{COD}}, S_{\triangle{FAO}}=\dfrac{1}{2}FO \cdot AO \cdot sin\angle{FOA}=\dfrac{1}{2}FO \cdot AO \cdot sin\angle{COD}\\
\shoveleft \implies S_{\triangle{ABO}} \cdot S_{\triangle{CDO}} \cdot S_{\triangle{EFO}}=S_{\triangle{BCO}} \cdot S_{\triangle{DEO}} \cdot S_{\triangle{FAO}}\\
\shoveleft \implies S_{\triangle{FAO}}=\dfrac{S_{\triangle{ABO}} \cdot S_{\triangle{CDO}} \cdot S_{\triangle{EFO}}}{S_{\triangle{BCO}} \cdot S_{\triangle{DEO}}}=\dfrac{12 * 8 * 2}{6 * 4}=\bbox[5px, border: 1px solid black]{8m^2}
\end{multline}\)
\(\begin{multline}
\shoveleft S_{\triangle{ABO}}=\dfrac{1}{2}AO\cdot BO \cdot sin{\angle{AOB}}, S_{\triangle{DEO}}=\dfrac{1}{2}DO \cdot EO \cdot sin\angle{DOE}=\dfrac{1}{2}DO \cdot EO \cdot sin\angle{AOB}\\
\shoveleft S_{\triangle{BCO}}=\dfrac{1}{2}BO\cdot CO \cdot sin{\angle{BOC}}, S_{\triangle{EFO}}=\dfrac{1}{2}EO \cdot FO \cdot sin\angle{EOF}=\dfrac{1}{2}EO \cdot FO \cdot sin\angle{BOC}\\
\shoveleft S_{\triangle{CDO}}=\dfrac{1}{2}CO\cdot DO \cdot sin{\angle{COD}}, S_{\triangle{FAO}}=\dfrac{1}{2}FO \cdot AO \cdot sin\angle{FOA}=\dfrac{1}{2}FO \cdot AO \cdot sin\angle{COD}\\
\shoveleft \implies S_{\triangle{ABO}} \cdot S_{\triangle{CDO}} \cdot S_{\triangle{EFO}}=S_{\triangle{BCO}} \cdot S_{\triangle{DEO}} \cdot S_{\triangle{FAO}}\\
\shoveleft \implies S_{\triangle{FAO}}=\dfrac{S_{\triangle{ABO}} \cdot S_{\triangle{CDO}} \cdot S_{\triangle{EFO}}}{S_{\triangle{BCO}} \cdot S_{\triangle{DEO}}}=\dfrac{12 * 8 * 2}{6 * 4}=\bbox[5px, border: 1px solid black]{8m^2}
\end{multline}\)
01/28/2024
Inscribed $\odot{O_1}$ is tangent to semi-circle $\odot{O}$ and its diameter $AB$. Find $tan(\angle{O_1AB}) + tan(\angle{O_1BA})$.
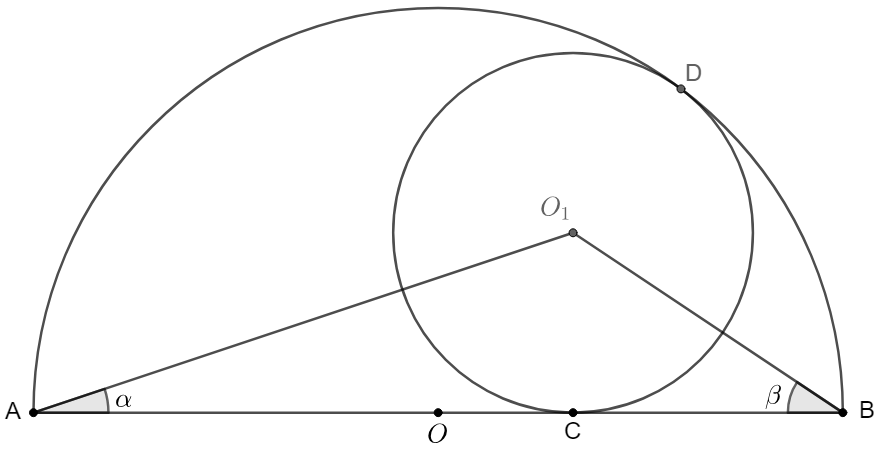
Solve:
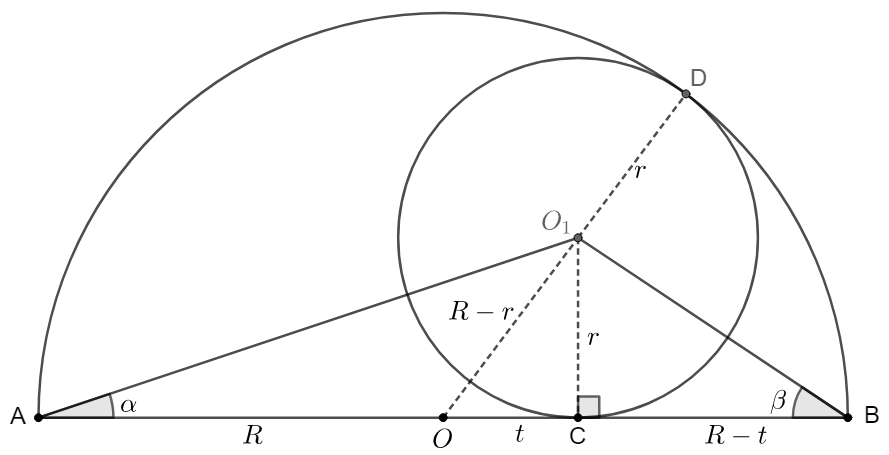 \(\begin{multline}\nonumber
\shoveleft \text{Let }\angle{O_1AB}=\alpha, \angle{O_1BA}=\beta, AO=R, CO_1=r, OC=t\\
\shoveleft \implies OO_1^2=OC^2+O_1C^2\implies (R-r)^2=r^2+t^2\\
\shoveleft \implies R^2-t^2=2Rr\\
\shoveleft tan(\angle{O_1AB}) + tan(\angle{O_1BA})=\dfrac{r}{R+t} + \dfrac{r}{R-t}\\
\shoveleft =\dfrac{2Rr}{R^2-r^2}=\bbox[5px, border: 1px solid black]{1}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Let }\angle{O_1AB}=\alpha, \angle{O_1BA}=\beta, AO=R, CO_1=r, OC=t\\
\shoveleft \implies OO_1^2=OC^2+O_1C^2\implies (R-r)^2=r^2+t^2\\
\shoveleft \implies R^2-t^2=2Rr\\
\shoveleft tan(\angle{O_1AB}) + tan(\angle{O_1BA})=\dfrac{r}{R+t} + \dfrac{r}{R-t}\\
\shoveleft =\dfrac{2Rr}{R^2-r^2}=\bbox[5px, border: 1px solid black]{1}
\end{multline}\)
01/29/2024
$A_1B_1, A_2B_2$ are focal chords of parabola. $D=A_1A_2 \cap B_1B_2$. Prove that $D$ is on the directrix of the parabola.
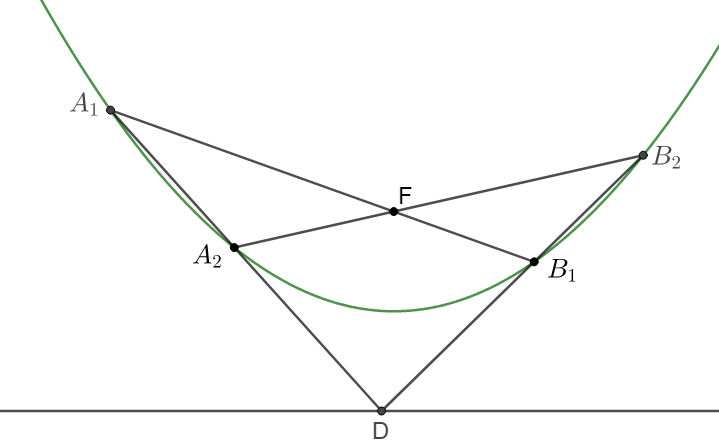
Prove:
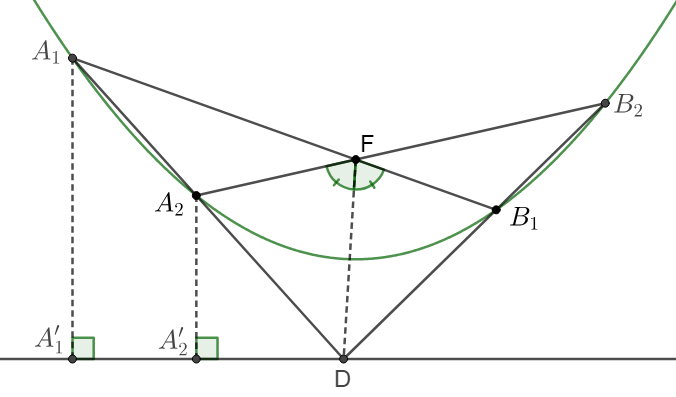 \(\begin{multline}\nonumber
\shoveleft \text{Suppose }A'_1, A'_2 \text{ are the projections of }A_1, A_2 \text{ on the directrix}\\
\shoveleft D \text{ is the intersection between extended }A_1A_2 \text{ and the directrix}.\\
\shoveleft \triangle{DA_1A'_1}\sim \triangle{DA_2A'_2} \implies \dfrac{DA_1}{DA_2}=\dfrac{A_1A'_1}{A_2A'_2}=\dfrac{FA_1}{FA_2}\\
\shoveleft \text{Via the exterior angle bisector theorem} \implies \angle{A_2FD}=\angle{DFB_1}\\
\shoveleft \implies D \text{ is on bisector of }\triangle{A_2FB_1}\\
\shoveleft \text{Similarly, let} D' \text{ be the intersection between extended }B_1B_2 \text{ and the directrix}\\
\shoveleft \implies D' \text{ is on disector of }\triangle{A_2FB_1}\implies D=D'\implies D=A_1A_2\cap B_1B_2\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Suppose }A'_1, A'_2 \text{ are the projections of }A_1, A_2 \text{ on the directrix}\\
\shoveleft D \text{ is the intersection between extended }A_1A_2 \text{ and the directrix}.\\
\shoveleft \triangle{DA_1A'_1}\sim \triangle{DA_2A'_2} \implies \dfrac{DA_1}{DA_2}=\dfrac{A_1A'_1}{A_2A'_2}=\dfrac{FA_1}{FA_2}\\
\shoveleft \text{Via the exterior angle bisector theorem} \implies \angle{A_2FD}=\angle{DFB_1}\\
\shoveleft \implies D \text{ is on bisector of }\triangle{A_2FB_1}\\
\shoveleft \text{Similarly, let} D' \text{ be the intersection between extended }B_1B_2 \text{ and the directrix}\\
\shoveleft \implies D' \text{ is on disector of }\triangle{A_2FB_1}\implies D=D'\implies D=A_1A_2\cap B_1B_2\blacksquare
\end{multline}\)
01/30/2024
$F$ is the focus of a parabola, $A,B$ are two points on the parabola and $S$ is the intersection between the two tangent lines of the parabola at $A, B$. $A’, B’$ are the projections of $A,B$ on the directrix. Prove that:
(1) $S$ is the circumcenter of $\triangle{FA’B’}$
(2) $\angle{FBS}=\angle{FB’A’}=\angle{FSA}, \angle{FAS}=\angle{FA’B’}=\angle{FSB}$
(3) $F$ is on line $AB$ if and only if $S$ is on line $A’B’$ and in this case, $SA\perp SB$
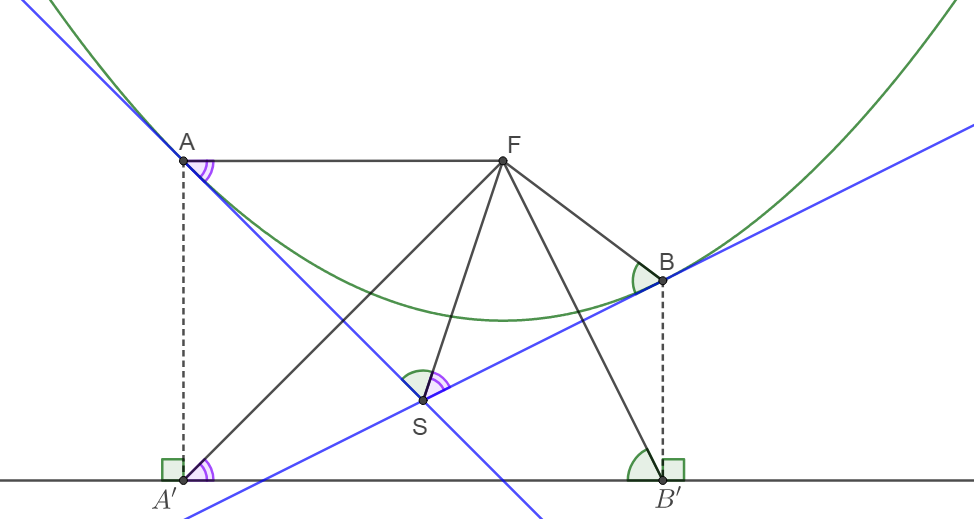
Prove:
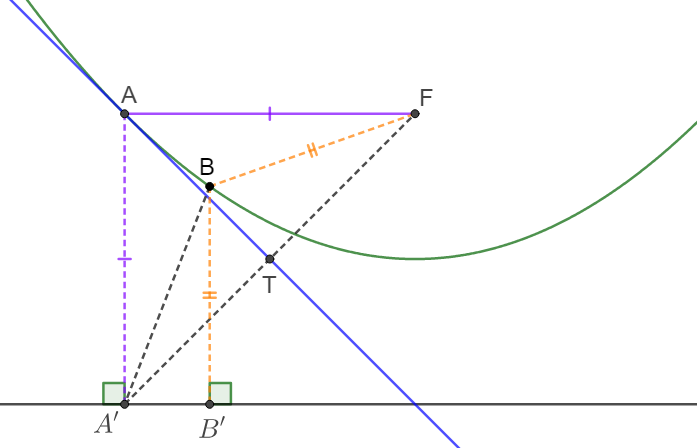
 \(\begin{multline}\nonumber
\shoveleft \boxed{\text{Reflective Properties of parabola:}}\\
\shoveleft \text{Let }A \text{ be a point on a parabola}\\
\shoveleft A' \text{ be the projection of }A \text{ on the directrix}\\
\shoveleft F \text{ be the focus of the parabola}\\
\shoveleft \implies \text{the tangent line of the parabola at }A \text{ bisects }\angle{FAA'}\\
\shoveleft \text{Prove: } \text{suppose the bisector of }\angle{FAA'} \text{ intersects the parabola in another point }B\\
\shoveleft \text{Let }B' \text{ be the projection of }B \text{ on the directrix} \implies BF=BB'\\
\shoveleft B \text{ is on bisector of }\angle{FAA'} \implies BF=BA' \implies BB'=BA' \text{ which is impossible}\\
\shoveleft \implies A \text{ is the only point of the parabola that is on the bisector of }\angle{FAA'}\\
\shoveleft \implies \text{the bisector of }\angle{FAA'} \text{ is the tangent line of parabola at }A\blacksquare\\
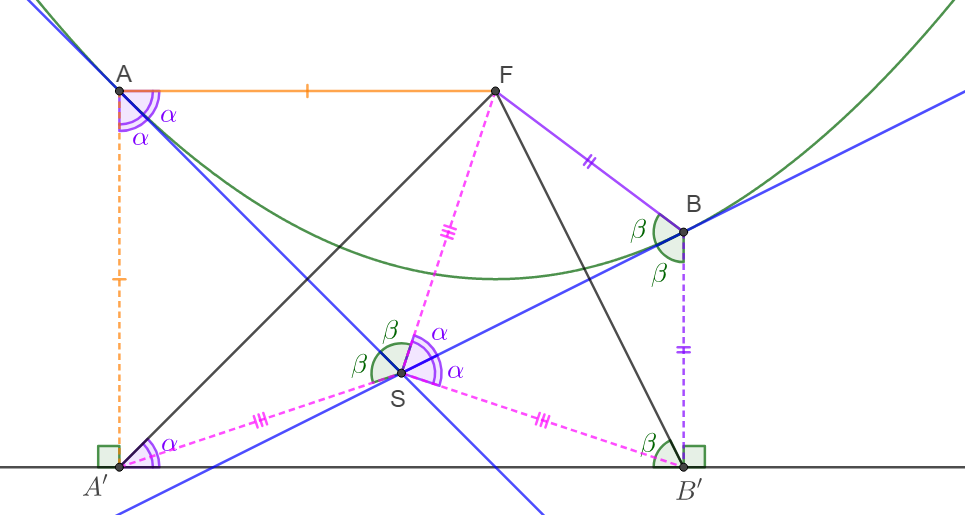
\shoveleft \implies SF=SA'=SB'\implies S \text{ is the circumcenter of }\triangle{SA'B'}\blacksquare\\
\shoveleft \implies \angle{FSB'}=2\angle{FA'B'}=2\angle{FSB}\implies \angle{FA'B'}=\angle{FSB}\\
\shoveleft \implies \angle{FAS}=\angle{A'AS}=90^{\circ}-\angle{AA'F}=\angle{FA'B'}=\angle{FSB}\blacksquare\\
\shoveleft \text{Similarly: }\angle{FBS}=\angle{FB'A'}=\angle{FSA}\blacksquare\\
\shoveleft \text{Let }\angle{FSB}=\angle{BSB'}=\angle{FA'B'}=\angle{FAS}=\angle{A'AS}=\alpha\\
\shoveleft \angle{FSA}=\angle{ASA'}=\angle{FB'A'}=\angle{FBS}=\angle{B'BS}=\beta\\
\shoveleft \angle{AFB}=\angle{AFS}+\angle{BFS}=180^{\circ}-\alpha-\beta+180^{\circ}-180^{\circ}-\alpha-\beta=\angle{A'SB'}\\
\shoveleft \implies \angle{AFB}=180^{\circ} \text{ if and only if }\angle{A'SB'}=180^{\circ}\\
\shoveleft \implies F \text{ is on }AB \text{ if and only if }S \text{ is on }A'B'\blacksquare\\
\shoveleft S \text{ is on }A'B'\implies \angle{A'SB'}=180^{\circ} \text{ if and only if }\alpha+\beta=90^{\circ}\implies SA \perp SB\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \boxed{\text{Reflective Properties of parabola:}}\\
\shoveleft \text{Let }A \text{ be a point on a parabola}\\
\shoveleft A' \text{ be the projection of }A \text{ on the directrix}\\
\shoveleft F \text{ be the focus of the parabola}\\
\shoveleft \implies \text{the tangent line of the parabola at }A \text{ bisects }\angle{FAA'}\\
\shoveleft \text{Prove: } \text{suppose the bisector of }\angle{FAA'} \text{ intersects the parabola in another point }B\\
\shoveleft \text{Let }B' \text{ be the projection of }B \text{ on the directrix} \implies BF=BB'\\
\shoveleft B \text{ is on bisector of }\angle{FAA'} \implies BF=BA' \implies BB'=BA' \text{ which is impossible}\\
\shoveleft \implies A \text{ is the only point of the parabola that is on the bisector of }\angle{FAA'}\\
\shoveleft \implies \text{the bisector of }\angle{FAA'} \text{ is the tangent line of parabola at }A\blacksquare\\
\shoveleft \implies SF=SA'=SB'\implies S \text{ is the circumcenter of }\triangle{SA'B'}\blacksquare\\
\shoveleft \implies \angle{FSB'}=2\angle{FA'B'}=2\angle{FSB}\implies \angle{FA'B'}=\angle{FSB}\\
\shoveleft \implies \angle{FAS}=\angle{A'AS}=90^{\circ}-\angle{AA'F}=\angle{FA'B'}=\angle{FSB}\blacksquare\\
\shoveleft \text{Similarly: }\angle{FBS}=\angle{FB'A'}=\angle{FSA}\blacksquare\\
\shoveleft \text{Let }\angle{FSB}=\angle{BSB'}=\angle{FA'B'}=\angle{FAS}=\angle{A'AS}=\alpha\\
\shoveleft \angle{FSA}=\angle{ASA'}=\angle{FB'A'}=\angle{FBS}=\angle{B'BS}=\beta\\
\shoveleft \angle{AFB}=\angle{AFS}+\angle{BFS}=180^{\circ}-\alpha-\beta+180^{\circ}-180^{\circ}-\alpha-\beta=\angle{A'SB'}\\
\shoveleft \implies \angle{AFB}=180^{\circ} \text{ if and only if }\angle{A'SB'}=180^{\circ}\\
\shoveleft \implies F \text{ is on }AB \text{ if and only if }S \text{ is on }A'B'\blacksquare\\
\shoveleft S \text{ is on }A'B'\implies \angle{A'SB'}=180^{\circ} \text{ if and only if }\alpha+\beta=90^{\circ}\implies SA \perp SB\blacksquare
\end{multline}\)
Notes:
- Two Tangents to Parabola on cut-the-knot site
- The previous problem on StackExchange
- Optical Property of the parabola from the book “Geometry of Conics” Page 15