12/08/2023
Prove that the extended lines from the centers of three excircles to the corresponding point of tangency are concurrent, and the segments from the centers of excircles to the concurrent point are congruent
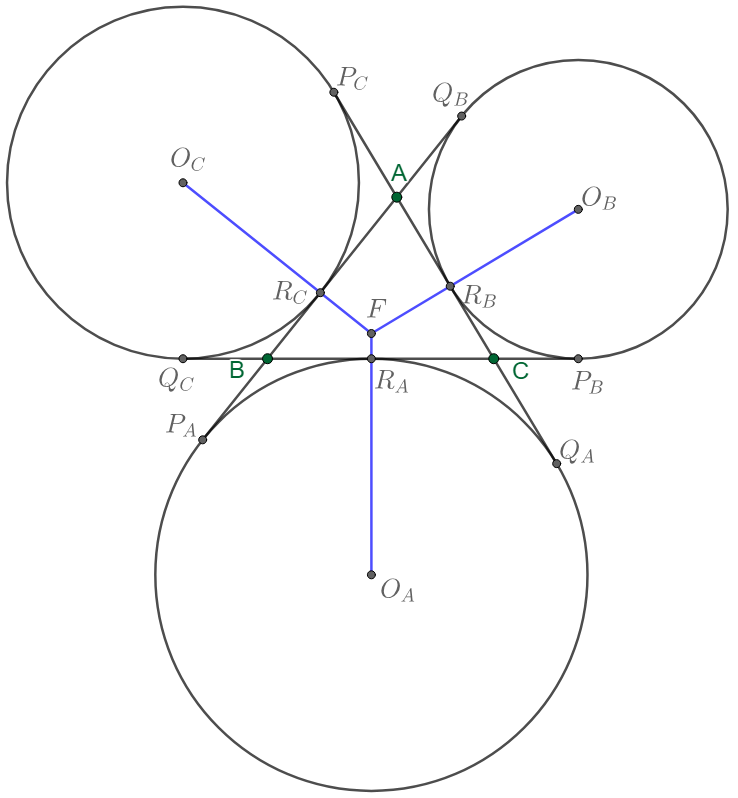
Prove 1:
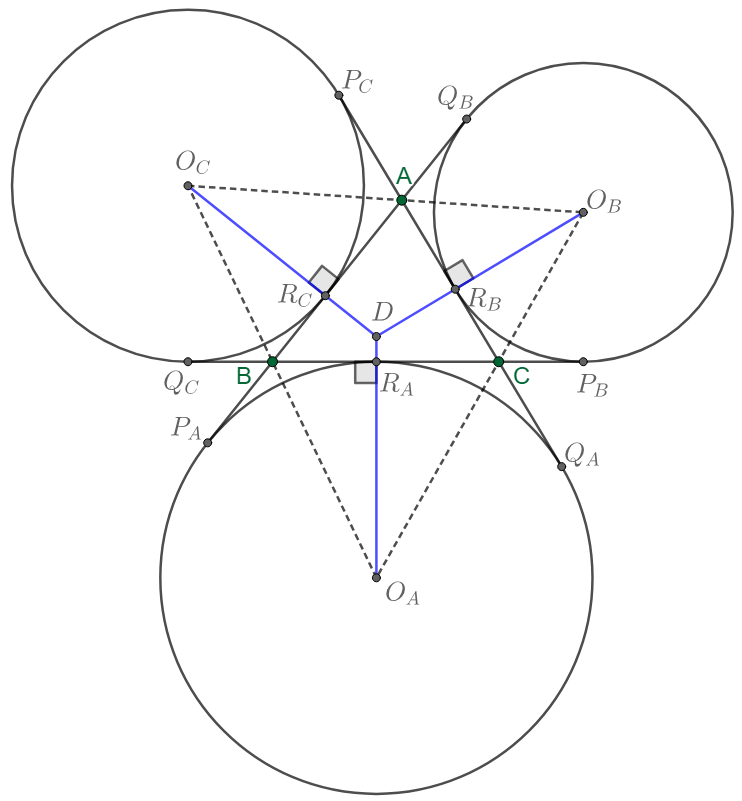 \(\begin{multline}\nonumber
\shoveleft \text{Concurrency:}\\
\shoveleft \text{Suppose }D_A=O_CR_C \cap O_BR_B, D_B=O_CR_C\cap O_AR_A, D_C=O_AR_A \cap O_BR_B\\
\shoveleft \angle{P_CAO_C}=\angle{O_CAR_C}=\angle{Q_BAO_B}=\angle{O_BAR_B} \implies O_CAO_B, O_BCO_A, O_ABO_C \text{ are collinear }\\
\shoveleft \angle{AO_CD_A}=\angle{AO_BD_A}, \angle{D_CO_BC}=\angle{D_BO_AC}, \angle{D_BO_AB}=\angle{D_BO_CB}\\
\shoveleft \text{By trigonometric version of Ceva Theorem, }D_A=D_B=D_C,\text{ concurrency is proven.}\\
\shoveleft \implies O_CD=O_BD=O_AD\blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft O_AO_C \text{ bisects }\angle{ABO_C}, O_BB \text{ bisects } \angle{ABC} \implies O_BB \perp O_AO_C\\
\shoveleft \text{Similarly }O_CC \perp O_AO_B, O_AA \perp O_BO_C \implies \\
\shoveleft \text{incenter of }\triangle{ABC}= \text{orthocenter of } \triangle{O_AO_BO_C}\\
\shoveleft \text{By Nagel's Theorem}, \text{ if } O \text{ is the circumcenter of }\triangle{O_AO_BO_C}\\
\shoveleft O_AA \text{ and }O_BB \text{ are two altitudes of }\triangle{O_AO_BO_C} \implies O_CC \perp AB\\
\shoveleft \implies O_CR_CO \text{ are collinear, similarly }O_BR_BO, O_CR_CO \text{ are collinear too}\\
\shoveleft \implies O_AR_A \cap O_BR_B \cap O_CR_C = O= \text{circumcenter of }\triangle{O_AO_BO_C}\\
\shoveleft \implies OO_A=OO_B=OO_C\blacksquare
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Concurrency:}\\
\shoveleft \text{Suppose }D_A=O_CR_C \cap O_BR_B, D_B=O_CR_C\cap O_AR_A, D_C=O_AR_A \cap O_BR_B\\
\shoveleft \angle{P_CAO_C}=\angle{O_CAR_C}=\angle{Q_BAO_B}=\angle{O_BAR_B} \implies O_CAO_B, O_BCO_A, O_ABO_C \text{ are collinear }\\
\shoveleft \angle{AO_CD_A}=\angle{AO_BD_A}, \angle{D_CO_BC}=\angle{D_BO_AC}, \angle{D_BO_AB}=\angle{D_BO_CB}\\
\shoveleft \text{By trigonometric version of Ceva Theorem, }D_A=D_B=D_C,\text{ concurrency is proven.}\\
\shoveleft \implies O_CD=O_BD=O_AD\blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft O_AO_C \text{ bisects }\angle{ABO_C}, O_BB \text{ bisects } \angle{ABC} \implies O_BB \perp O_AO_C\\
\shoveleft \text{Similarly }O_CC \perp O_AO_B, O_AA \perp O_BO_C \implies \\
\shoveleft \text{incenter of }\triangle{ABC}= \text{orthocenter of } \triangle{O_AO_BO_C}\\
\shoveleft \text{By Nagel's Theorem}, \text{ if } O \text{ is the circumcenter of }\triangle{O_AO_BO_C}\\
\shoveleft O_AA \text{ and }O_BB \text{ are two altitudes of }\triangle{O_AO_BO_C} \implies O_CC \perp AB\\
\shoveleft \implies O_CR_CO \text{ are collinear, similarly }O_BR_BO, O_CR_CO \text{ are collinear too}\\
\shoveleft \implies O_AR_A \cap O_BR_B \cap O_CR_C = O= \text{circumcenter of }\triangle{O_AO_BO_C}\\
\shoveleft \implies OO_A=OO_B=OO_C\blacksquare
\end{multline}\)
12/10/2023
Prove that if a triangle has a $60^{\circ}$ angle and $H,I,O$ are its orthocenter, incenter, circumcenter respectively, then $HI=IO$.
Prove:
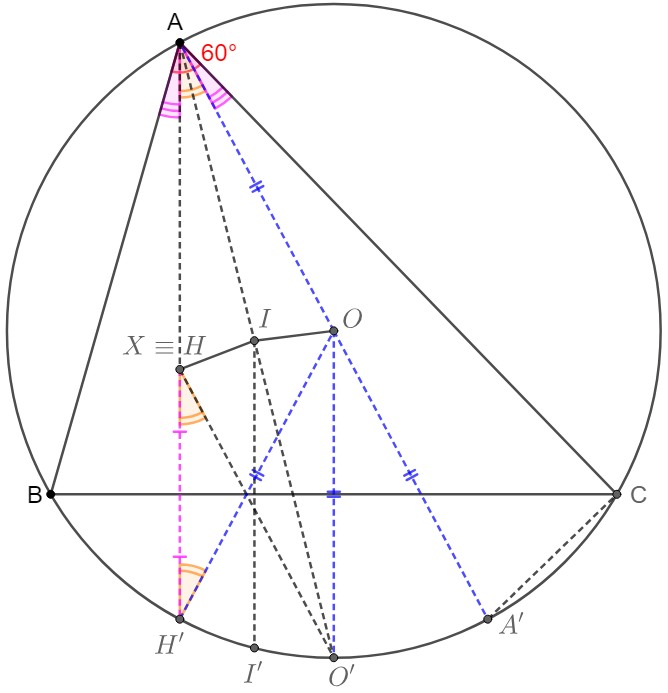 .
\(\begin{multline}\nonumber
\shoveleft \text{Let }H', I', O' \text{ be the reflection point of }H, I, O \text{ respectively about }BC, A' \text{ be the antipode of }A \text{ on } \odot{O}\\
\shoveleft BH\perp AC, CH\perp AB \implies \angle{BAC}+\angle{BHC}=180^{\circ} \implies \angle{BAC}+\angle{BH'C}=180^{\circ}\\
\shoveleft \angle{BAC}+\angle{BI'C}=\angle{BAC}+\angle{BIC}=60^{\circ}+180^{\circ}-\dfrac{\angle{ABC}+\angle{ACB}}{2}=240^{\circ}-\dfrac{120^{\circ}}{2}=180^{\circ}\\
\shoveleft \angle{BAC}+\angle{BO'C}=\angle{BAC}+\angle{BOC}=60^{\circ}+120^{\circ}=180^{\circ} \implies H', I',O' \text{ are all on }\odot{O}\\
\shoveleft H,O \text{ are isogonal conjugates} \implies \angle{BAH}=\angle{OAC} (\angle{BAH}=90^{\circ}-\angle{ABC}=90^{\circ}-\angle{AA'C}=\angle{OAC})\\
\shoveleft \implies \angle{HAI}=\angle{BAI}-\angle{BAH}=\angle{IAC}-\angle{OAC}=\angle{IAO}, AH \perp BC, OO' \perp BC \implies AH\parallel OO'\\
\shoveleft \text{By reflection we know }\angle{H'HO'}=\angle{HH'O}=\angle{HAO}\implies HO' \parallel AO \implies AOO'H \text{ is parallelogram}\\
\shoveleft AO=OO' \implies AH=OO'=AO \implies \triangle{AHI} \cong \triangle{AOI} \implies HI=IO \blacksquare\\
\end{multline}\)
.
\(\begin{multline}\nonumber
\shoveleft \text{Let }H', I', O' \text{ be the reflection point of }H, I, O \text{ respectively about }BC, A' \text{ be the antipode of }A \text{ on } \odot{O}\\
\shoveleft BH\perp AC, CH\perp AB \implies \angle{BAC}+\angle{BHC}=180^{\circ} \implies \angle{BAC}+\angle{BH'C}=180^{\circ}\\
\shoveleft \angle{BAC}+\angle{BI'C}=\angle{BAC}+\angle{BIC}=60^{\circ}+180^{\circ}-\dfrac{\angle{ABC}+\angle{ACB}}{2}=240^{\circ}-\dfrac{120^{\circ}}{2}=180^{\circ}\\
\shoveleft \angle{BAC}+\angle{BO'C}=\angle{BAC}+\angle{BOC}=60^{\circ}+120^{\circ}=180^{\circ} \implies H', I',O' \text{ are all on }\odot{O}\\
\shoveleft H,O \text{ are isogonal conjugates} \implies \angle{BAH}=\angle{OAC} (\angle{BAH}=90^{\circ}-\angle{ABC}=90^{\circ}-\angle{AA'C}=\angle{OAC})\\
\shoveleft \implies \angle{HAI}=\angle{BAI}-\angle{BAH}=\angle{IAC}-\angle{OAC}=\angle{IAO}, AH \perp BC, OO' \perp BC \implies AH\parallel OO'\\
\shoveleft \text{By reflection we know }\angle{H'HO'}=\angle{HH'O}=\angle{HAO}\implies HO' \parallel AO \implies AOO'H \text{ is parallelogram}\\
\shoveleft AO=OO' \implies AH=OO'=AO \implies \triangle{AHI} \cong \triangle{AOI} \implies HI=IO \blacksquare\\
\end{multline}\)
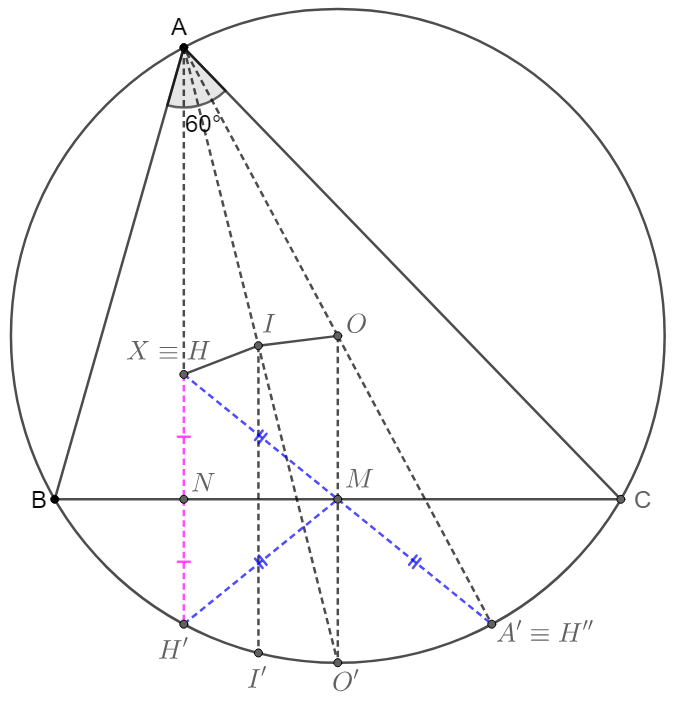 .
\(\begin{multline}
\shoveleft \text{Generally for any }\triangle{ABC}, \text{let }H'' \text{ be the reflection point of } H \text{ about }M \implies H''\equiv A' \text{ also on }\odot{O}\\
\shoveleft \text{Let }N \text{ be the foot of altitude on }BC \implies AN \perp BC, AN\cap BC=N, M \text{ is the midpoint of }BC\\
\shoveleft BM=MC \implies OM \perp BC, \text{ since }AN \perp BC \implies AN \parallel OM\\
\shoveleft \text{Extend }A'M \text{ and intersect with }AN \text{ at }X, \text{ will prove }X\equiv N\\
\shoveleft AO=OA' \implies A'M=MX, X \text{ is the reflection of }A' \text{ about }M\\
\shoveleft \text{Extend } AN \text{ and intersect with }\odot{O} \text{ at }H' \implies A'H' \perp AN \implies H'A' \parallel BC \implies HN=NH'\\
\shoveleft \implies H' \text{ is the reflection point of }H \text{ about BC }\implies X \equiv H \implies \text{ the reflection of }H \text{ is }H'' \equiv A' \text{ on }\odot{O}\\
\end{multline}\)
.
\(\begin{multline}
\shoveleft \text{Generally for any }\triangle{ABC}, \text{let }H'' \text{ be the reflection point of } H \text{ about }M \implies H''\equiv A' \text{ also on }\odot{O}\\
\shoveleft \text{Let }N \text{ be the foot of altitude on }BC \implies AN \perp BC, AN\cap BC=N, M \text{ is the midpoint of }BC\\
\shoveleft BM=MC \implies OM \perp BC, \text{ since }AN \perp BC \implies AN \parallel OM\\
\shoveleft \text{Extend }A'M \text{ and intersect with }AN \text{ at }X, \text{ will prove }X\equiv N\\
\shoveleft AO=OA' \implies A'M=MX, X \text{ is the reflection of }A' \text{ about }M\\
\shoveleft \text{Extend } AN \text{ and intersect with }\odot{O} \text{ at }H' \implies A'H' \perp AN \implies H'A' \parallel BC \implies HN=NH'\\
\shoveleft \implies H' \text{ is the reflection point of }H \text{ about BC }\implies X \equiv H \implies \text{ the reflection of }H \text{ is }H'' \equiv A' \text{ on }\odot{O}\\
\end{multline}\)
12/15/2023
$D$ is a point on side $BC$ of $\triangle{ABC}$ such that $\angle{ACB}=40^{\circ}, \angle{ADC}=30^{\circ}, AB=CD$, find $\angle{ABC}$.
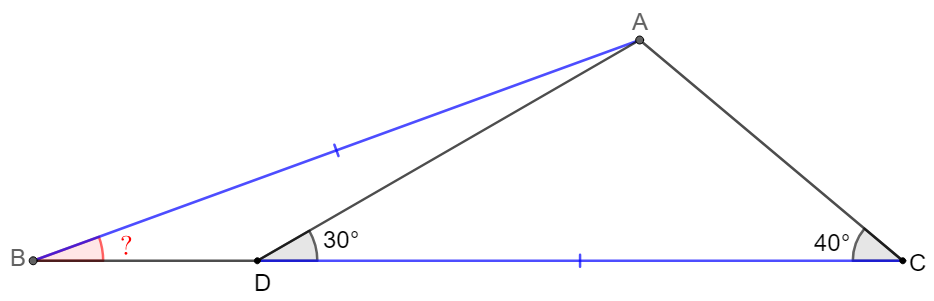
Solve 1:
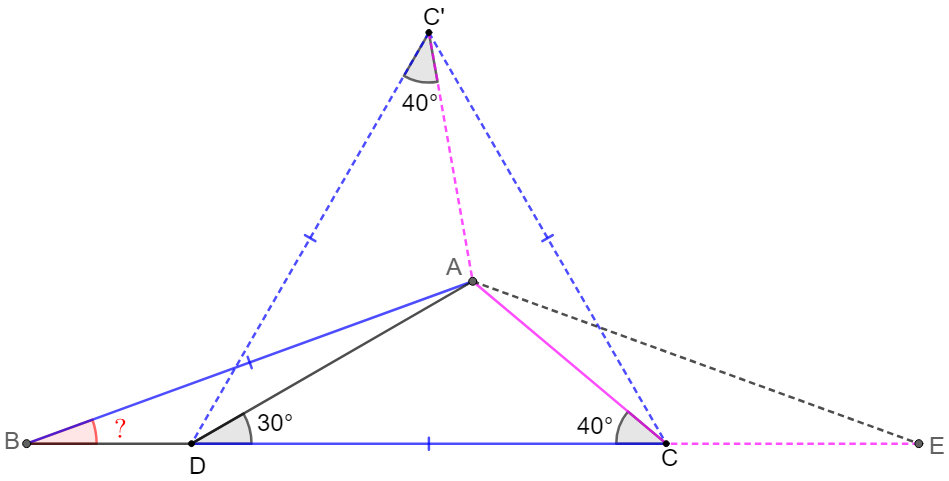 \(\begin{multline}\nonumber
\shoveleft \text{Let } C' \text{ be reflection of } C \text{ about } AD, \text{ and extend }DC \text{ to }E \text{ such that } AC=CE\\
\shoveleft \implies CA=C'A, \angle{ADC'}=\angle{ADC}=30^{\circ}, \angle{ACD}=\angle{AC'D}=40^{\circ}, \angle{CAE}=\angle{CEA}=20^{\circ}\\
\shoveleft \implies \triangle{CDC'} \text{ is equilateral} \implies \angle{ACC'}=\angle{AC'C}=20^{\circ}\implies \triangle{CAC'}\cong \triangle{ACE} \\
\shoveleft \implies AE=CC'=CD=AB\implies \angle{ABC}=\angle{CEA}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
Solve 2:
\(\begin{multline}\nonumber
\shoveleft \text{Let } C' \text{ be reflection of } C \text{ about } AD, \text{ and extend }DC \text{ to }E \text{ such that } AC=CE\\
\shoveleft \implies CA=C'A, \angle{ADC'}=\angle{ADC}=30^{\circ}, \angle{ACD}=\angle{AC'D}=40^{\circ}, \angle{CAE}=\angle{CEA}=20^{\circ}\\
\shoveleft \implies \triangle{CDC'} \text{ is equilateral} \implies \angle{ACC'}=\angle{AC'C}=20^{\circ}\implies \triangle{CAC'}\cong \triangle{ACE} \\
\shoveleft \implies AE=CC'=CD=AB\implies \angle{ABC}=\angle{CEA}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
Solve 2:
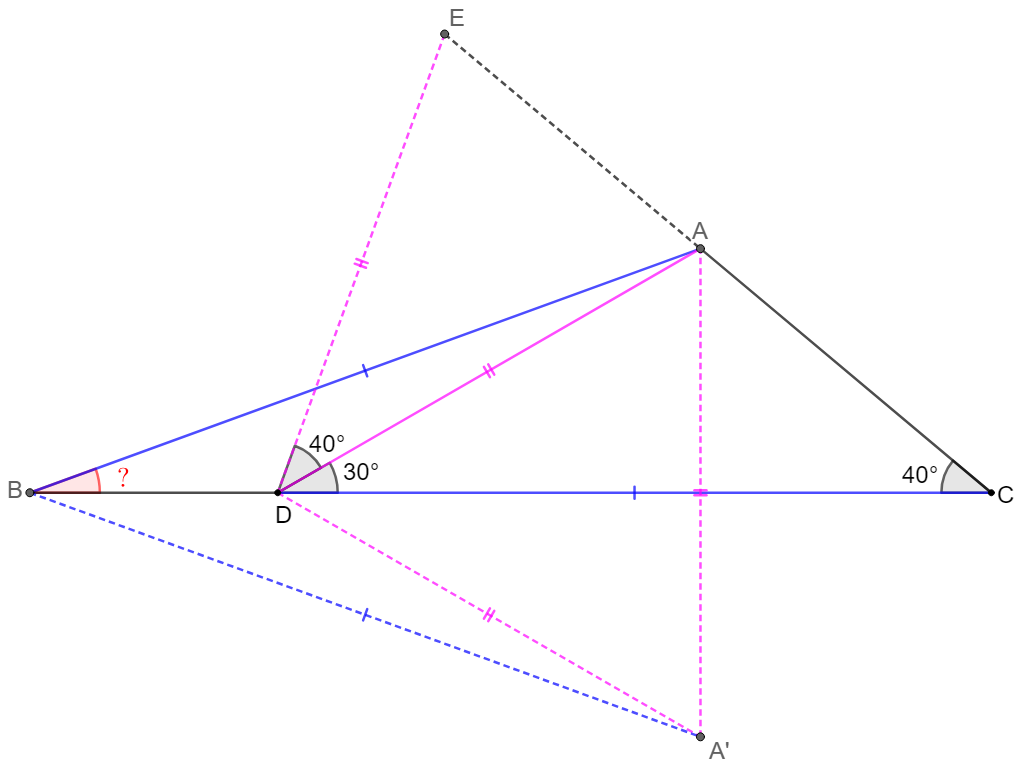 \(\begin{multline}
\shoveleft \text{Let } A' \text{ be reflection of } A \text{ about } BC, \text{ and extend }CA \text{ to }E \text{ such that } CD=CE\\
\shoveleft \implies \angle{CDE}=\angle{CED}=70^{\circ}, A'B=AB, AD=A'D, \angle{ADC}=\angle{A'DC}=30^{\circ}\\
\shoveleft \implies \angle{ADE}=40^{\circ},\triangle{AA'D}\text{ is equilateral} \implies \angle{EAD}=\angle{CED}=70^{\circ}\\
\shoveleft \implies AA'=AD=DE \implies \triangle{ABA'}\cong\triangle{DCE}\implies\angle{ABA'}=\angle{DCE}=40^{\circ}\\
\shoveleft \implies \angle{ABC}=\dfrac{40^{\circ}}{2}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
Solve 3:
\(\begin{multline}
\shoveleft \text{Let } A' \text{ be reflection of } A \text{ about } BC, \text{ and extend }CA \text{ to }E \text{ such that } CD=CE\\
\shoveleft \implies \angle{CDE}=\angle{CED}=70^{\circ}, A'B=AB, AD=A'D, \angle{ADC}=\angle{A'DC}=30^{\circ}\\
\shoveleft \implies \angle{ADE}=40^{\circ},\triangle{AA'D}\text{ is equilateral} \implies \angle{EAD}=\angle{CED}=70^{\circ}\\
\shoveleft \implies AA'=AD=DE \implies \triangle{ABA'}\cong\triangle{DCE}\implies\angle{ABA'}=\angle{DCE}=40^{\circ}\\
\shoveleft \implies \angle{ABC}=\dfrac{40^{\circ}}{2}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
Solve 3:
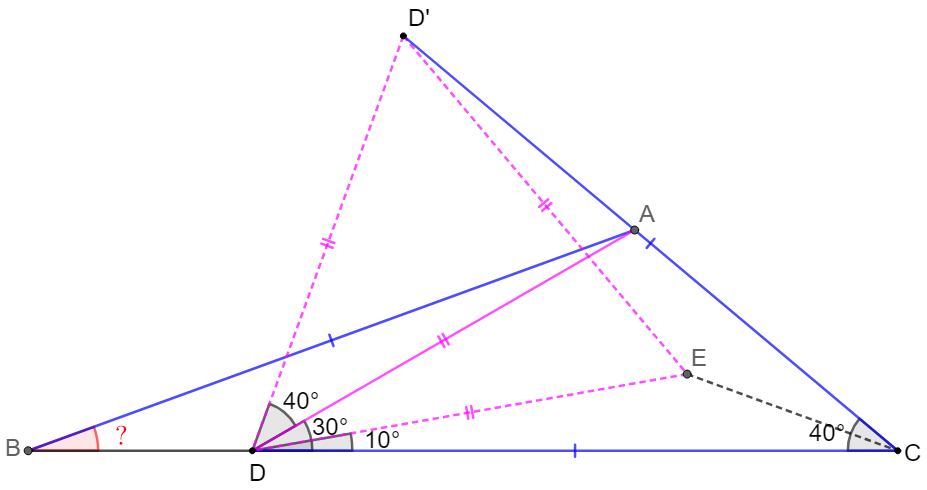 \(\begin{multline}
\shoveleft \text{Extend } CA \text{ to } D' \text{ such that }CD=CD'=AB, \text{ let } E \text{ inside } \triangle{DCD'} \text{ such that } \triangle{DED'} \text{ is equilateral }\\
\shoveleft \implies D'E=DE=DD',\angle{D'EC}=150^{\circ}=\angle{BDC}, \angle{D'DC}=\angle{DD'C}=70^{\circ} \implies \angle{D'DA}=40^{\circ}\\
\shoveleft \implies \angle{D'AD}=\angle{DD'C} \implies DD'=DA=DE \implies \triangle{ABD}\cong \triangle{DCE}\text{(SSA for obtuse triangle)}\\
\shoveleft \implies \angle{ABC}=\angle{DCE}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Extend } CA \text{ to } D' \text{ such that }CD=CD'=AB, \text{ let } E \text{ inside } \triangle{DCD'} \text{ such that } \triangle{DED'} \text{ is equilateral }\\
\shoveleft \implies D'E=DE=DD',\angle{D'EC}=150^{\circ}=\angle{BDC}, \angle{D'DC}=\angle{DD'C}=70^{\circ} \implies \angle{D'DA}=40^{\circ}\\
\shoveleft \implies \angle{D'AD}=\angle{DD'C} \implies DD'=DA=DE \implies \triangle{ABD}\cong \triangle{DCE}\text{(SSA for obtuse triangle)}\\
\shoveleft \implies \angle{ABC}=\angle{DCE}=\bbox[5px, border: 1px solid black]{20^{\circ}}
\end{multline}\)
12/16/2023
$\angle{CAB}=\angle{ABC}=30^{\circ}$ in $\triangle{ABC}$. $D$ is a point on side $BC$ and $E$ is on extended $AD$ such that $AE\perp BE$. Extended $AC, BE$ intercept at $F$. Prove that $\angle{CDF}=2\angle{ADC}, AC+CD=CF+FD$
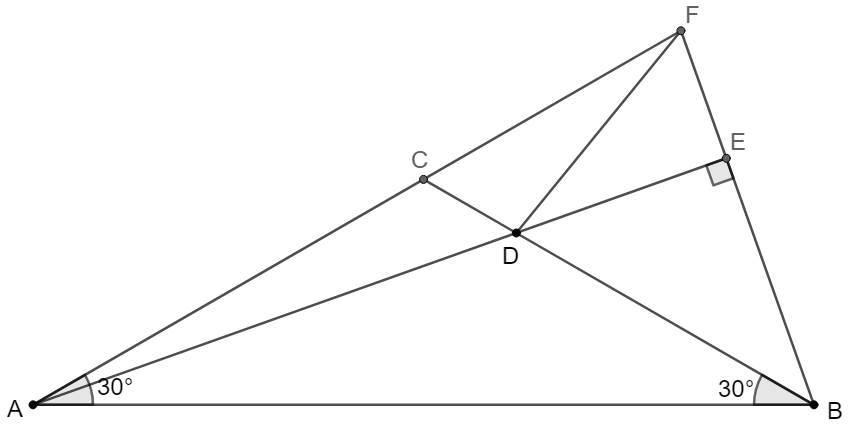
Prove:
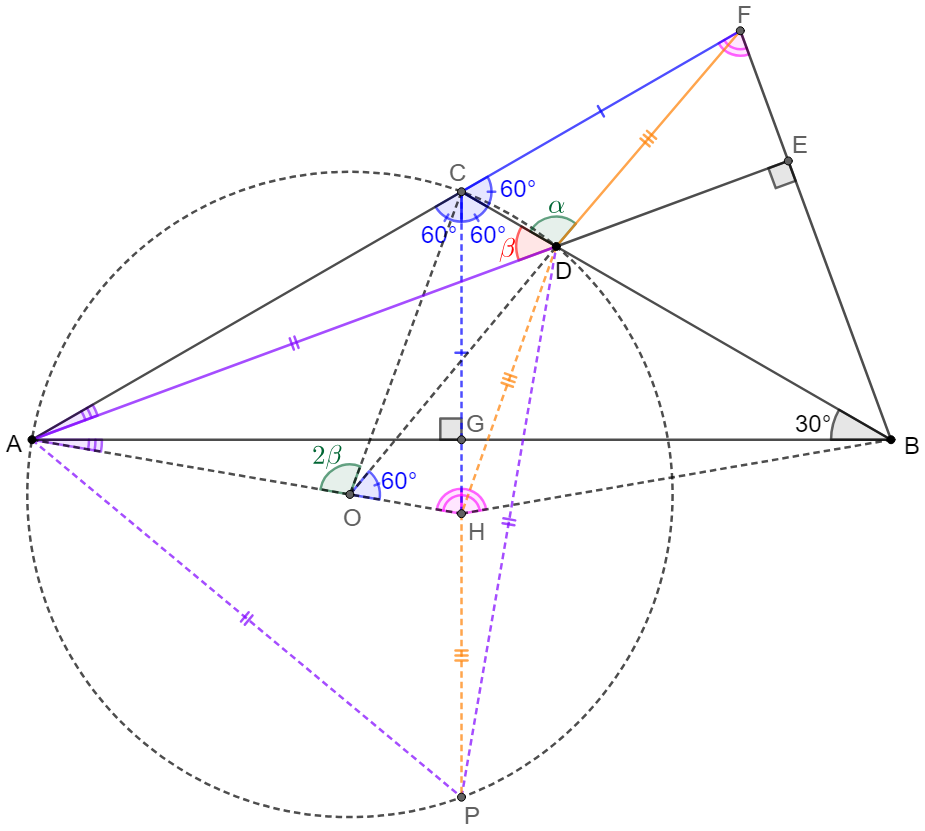 \(\begin{multline}\nonumber
\shoveleft \text{Make } CH \text{ bisect } \angle{ACB} \text{ and } CH=CF, CH\cap AB=G\\
\shoveleft \implies \angle{ACH}=\angle{BCH}=\angle{BCF}=60^{\circ} \implies \triangle{BCH}\cong\triangle{BCF}, \triangle{CDH}\cong\triangle{CDF}\\
\shoveleft \angle{BFC}=\angle{BHC}=\angle{AHC} \implies \angle{GAH} = \angle{EAF} \implies \angle{DAH}=\angle{CAG}=30^{\circ}\\
\shoveleft \text{Let } O \text{ be circumcenter of }\triangle{ACD} \implies AO=OD, \angle{AOD}=2(180^{\circ}-\angle{ACD})=120^{\circ}\\
\shoveleft \implies \angle{OAD}=30^{\circ}=\angle{HAD}\implies AOH \text{ are collinear}, \angle{HOD}=180^{\circ}-\angle{AOD}=60^{\circ}=\angle{HCD}\\
\shoveleft \implies CDHO \text{ is cyclic}\implies \angle{AOC}=2\angle{CDA}=\angle{CDH}=\angle{CDF}\implies \angle{CDF}=2\angle{CDA}\blacksquare\\
\shoveleft \text{Let }\triangle{PAD} \text{ be equilateral triangle }\implies P \text{ is on the circumcircle of }\triangle{ACD} \text{ and }CGHP \text{ are collinear}\\
\shoveleft \angle{OAD}=30^{\circ}\implies HP=HD=FD\implies AD\cdot PC=AD \cdot(CH+DF)=AD \cdot(CF+FD)\\
\shoveleft =AC\cdot PD+AP \cdot CD=AD \cdot (AC+CD)\implies AC+CD=CF+FD\blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft \text{Make } CH \text{ bisect } \angle{ACB} \text{ and } CH=CF, CH\cap AB=G\\
\shoveleft \implies \angle{ACH}=\angle{BCH}=\angle{BCF}=60^{\circ} \implies \triangle{BCH}\cong\triangle{BCF}, \triangle{CDH}\cong\triangle{CDF}\\
\shoveleft \angle{BFC}=\angle{BHC}=\angle{AHC} \implies \angle{GAH} = \angle{EAF} \implies \angle{DAH}=\angle{CAG}=30^{\circ}\\
\shoveleft \text{Let } O \text{ be circumcenter of }\triangle{ACD} \implies AO=OD, \angle{AOD}=2(180^{\circ}-\angle{ACD})=120^{\circ}\\
\shoveleft \implies \angle{OAD}=30^{\circ}=\angle{HAD}\implies AOH \text{ are collinear}, \angle{HOD}=180^{\circ}-\angle{AOD}=60^{\circ}=\angle{HCD}\\
\shoveleft \implies CDHO \text{ is cyclic}\implies \angle{AOC}=2\angle{CDA}=\angle{CDH}=\angle{CDF}\implies \angle{CDF}=2\angle{CDA}\blacksquare\\
\shoveleft \text{Let }\triangle{PAD} \text{ be equilateral triangle }\implies P \text{ is on the circumcircle of }\triangle{ACD} \text{ and }CGHP \text{ are collinear}\\
\shoveleft \angle{OAD}=30^{\circ}\implies HP=HD=FD\implies AD\cdot PC=AD \cdot(CH+DF)=AD \cdot(CF+FD)\\
\shoveleft =AC\cdot PD+AP \cdot CD=AD \cdot (AC+CD)\implies AC+CD=CF+FD\blacksquare
\end{multline}\)
Prove 2:
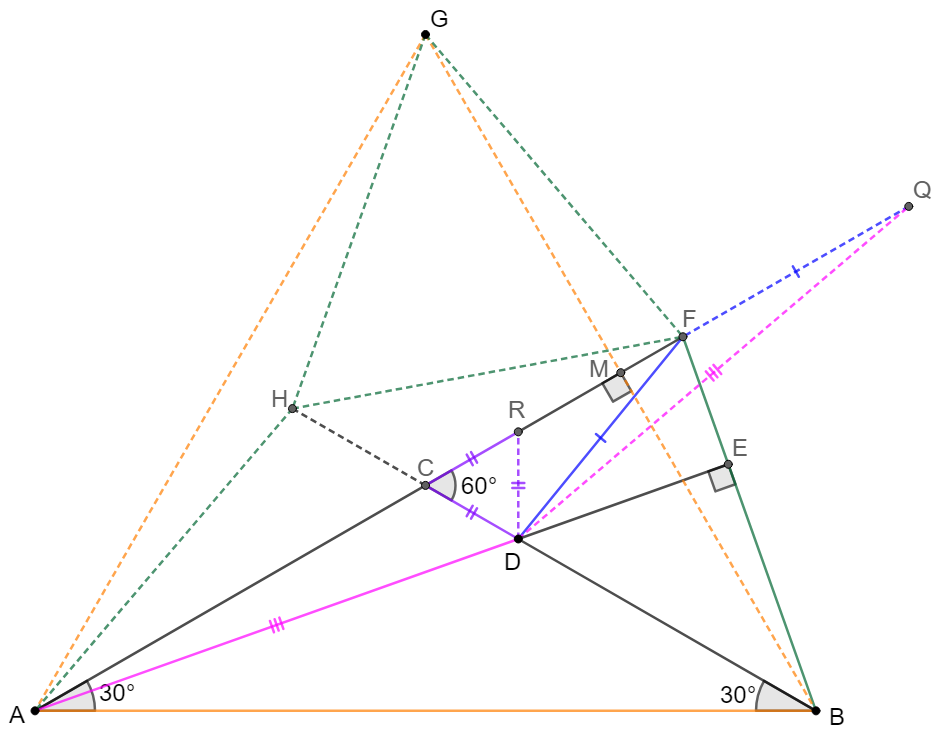 \(\begin{multline}
\shoveleft \text{Let }G\text{ be the reflection of } B \text{ about } AC \implies \triangle{ABG} \text{ is equilateral}, FG=FB,BG\perp AF\\
\shoveleft \text{Let }AF\cap BG=M \implies AMFB\text{ is cyclic} \implies \angle{CAD}=\angle{FBG}=\angle{FGB}=\angle{CGD}\\
\shoveleft \text{ Make }H \text{ in }\triangle{AFG} \text{ such that }\triangle{AGH} \text{ is equilateral }\implies \triangle{AGH}\cong\triangle{BGF}\implies AH=GH\\
\shoveleft \implies BCH \text{ are collinear}, \angle{GAH}=\angle{CAD} \implies \angle{HGD}=\angle{HAD}=\angle{GAC}=30^{\circ}\\
\shoveleft \implies \triangle{HAD}\cong\triangle{HGD}\cong\triangle{FGD}\implies \angle{CDF}=2\angle{CDA}\blacksquare\\
\shoveleft \angle{CAD}=60^{\circ}-\angle{CDA}, \angle{CFD}=180^{\circ}-60^{\circ}-\angle{CDF}=120^{\circ}-2\angle{CDA}=2\angle{CAD}\\
\shoveleft \text{Extend }CF \text{ to }Q \text{ such that }CF=FQ, \text{ make }R \text{ on }CF \text{ such that }CD=CR\\
\shoveleft \implies \angle{CAD}=\angle{FQD} \implies AD=QD, \angle{ARD}=\angle{FCD}\implies\triangle{ARD}\cong\triangle{QCD}\\
\shoveleft \implies AR=AC+CR=AC+CD=CQ=CF+FQ=CF+FD\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }G\text{ be the reflection of } B \text{ about } AC \implies \triangle{ABG} \text{ is equilateral}, FG=FB,BG\perp AF\\
\shoveleft \text{Let }AF\cap BG=M \implies AMFB\text{ is cyclic} \implies \angle{CAD}=\angle{FBG}=\angle{FGB}=\angle{CGD}\\
\shoveleft \text{ Make }H \text{ in }\triangle{AFG} \text{ such that }\triangle{AGH} \text{ is equilateral }\implies \triangle{AGH}\cong\triangle{BGF}\implies AH=GH\\
\shoveleft \implies BCH \text{ are collinear}, \angle{GAH}=\angle{CAD} \implies \angle{HGD}=\angle{HAD}=\angle{GAC}=30^{\circ}\\
\shoveleft \implies \triangle{HAD}\cong\triangle{HGD}\cong\triangle{FGD}\implies \angle{CDF}=2\angle{CDA}\blacksquare\\
\shoveleft \angle{CAD}=60^{\circ}-\angle{CDA}, \angle{CFD}=180^{\circ}-60^{\circ}-\angle{CDF}=120^{\circ}-2\angle{CDA}=2\angle{CAD}\\
\shoveleft \text{Extend }CF \text{ to }Q \text{ such that }CF=FQ, \text{ make }R \text{ on }CF \text{ such that }CD=CR\\
\shoveleft \implies \angle{CAD}=\angle{FQD} \implies AD=QD, \angle{ARD}=\angle{FCD}\implies\triangle{ARD}\cong\triangle{QCD}\\
\shoveleft \implies AR=AC+CR=AC+CD=CQ=CF+FQ=CF+FD\blacksquare
\end{multline}\)
12/20/2023
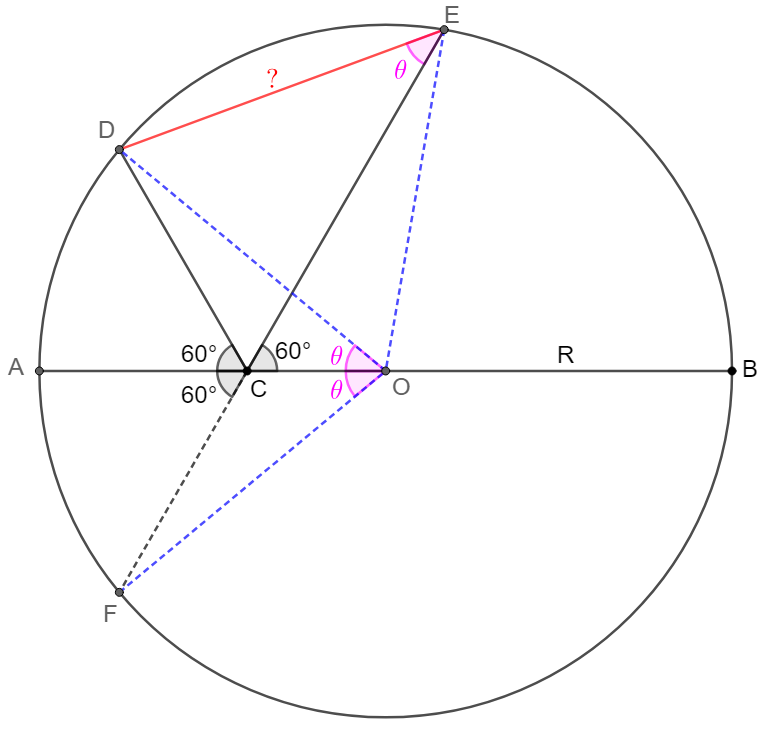
$C$ is a point on diameter $AB$ of $\odot{O}$, $AB=2R$, $D,E$ are two points on the circle such that $\angle{ACD}=\angle{ECB}=60^{\circ}$, find $DE$.
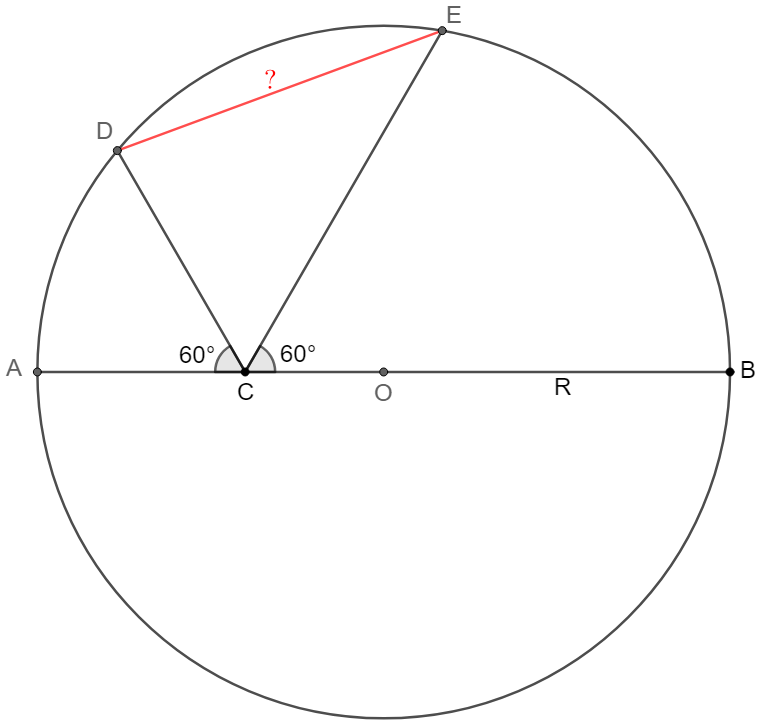
Solve:
 \(\begin{multline}
\shoveleft \text{Let }F \text{ be the reflection of }D \text{ about }AB\implies \angle{FCE}=\angle{ACO}\\
\shoveleft \implies FCE \text{ are collinear }\text{(as long as }\angle{ACD}=\angle{BCE}\text{)}\\
\shoveleft \implies \angle{AOD}=\angle{AOF}, \angle{DOF}=2\angle{DEF} \implies \angle{AOD}=\angle{DEF}\\
\shoveleft \implies CDEO \text{ is cyclic}\implies \angle{DOE}=\angle{DCE} \\
\shoveleft \text{ (This conclusion is always true for any }\angle{ACD}=\angle{BCE} \text{ value)}\\
\shoveleft \angle{ACD}=60^{\circ} \implies \angle{DOE}=60^{\circ}\implies DE=\bbox[5px, border: 1px solid black]{R}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }F \text{ be the reflection of }D \text{ about }AB\implies \angle{FCE}=\angle{ACO}\\
\shoveleft \implies FCE \text{ are collinear }\text{(as long as }\angle{ACD}=\angle{BCE}\text{)}\\
\shoveleft \implies \angle{AOD}=\angle{AOF}, \angle{DOF}=2\angle{DEF} \implies \angle{AOD}=\angle{DEF}\\
\shoveleft \implies CDEO \text{ is cyclic}\implies \angle{DOE}=\angle{DCE} \\
\shoveleft \text{ (This conclusion is always true for any }\angle{ACD}=\angle{BCE} \text{ value)}\\
\shoveleft \angle{ACD}=60^{\circ} \implies \angle{DOE}=60^{\circ}\implies DE=\bbox[5px, border: 1px solid black]{R}
\end{multline}\)
12/21/2023
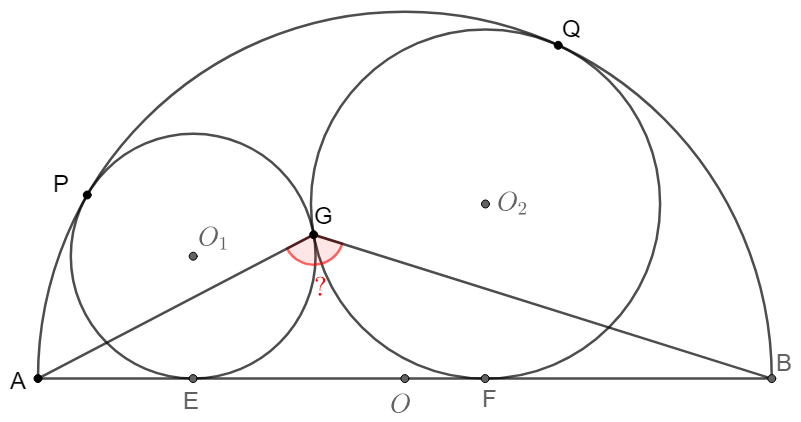
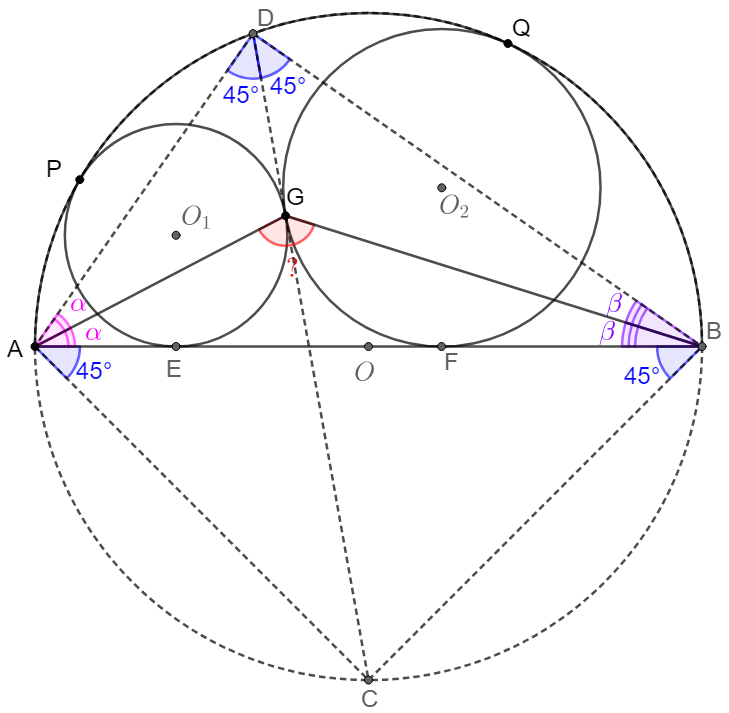
$\odot{O_1}, \odot{O_2}$ and tangent to each other at $G$ and inscribed inside semi-circle $\odot{O}$ with $AB$ as diameter. Find $\angle{AGB}$.
Solve:
 \(\begin{multline}
\shoveleft \text{From the insribed tangent circles model we know }G \text{ is the incenter of }\triangle{DAB}\\
\shoveleft \implies \angle{AGB}=\angle{ADB}+\dfrac{\angle{DAB}+\angle{DBA}}{2}=90^{\circ}+\dfrac{90^{\circ}}{2}=\bbox[5px, border: 1px solid black]{135^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{From the insribed tangent circles model we know }G \text{ is the incenter of }\triangle{DAB}\\
\shoveleft \implies \angle{AGB}=\angle{ADB}+\dfrac{\angle{DAB}+\angle{DBA}}{2}=90^{\circ}+\dfrac{90^{\circ}}{2}=\bbox[5px, border: 1px solid black]{135^{\circ}}
\end{multline}\)
12/29/2023
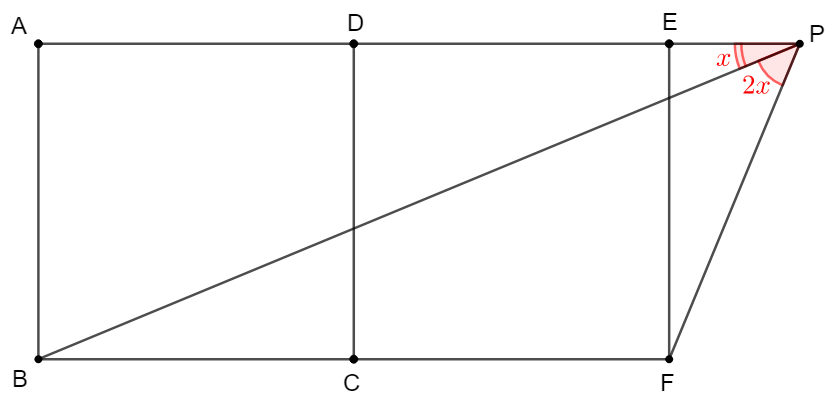
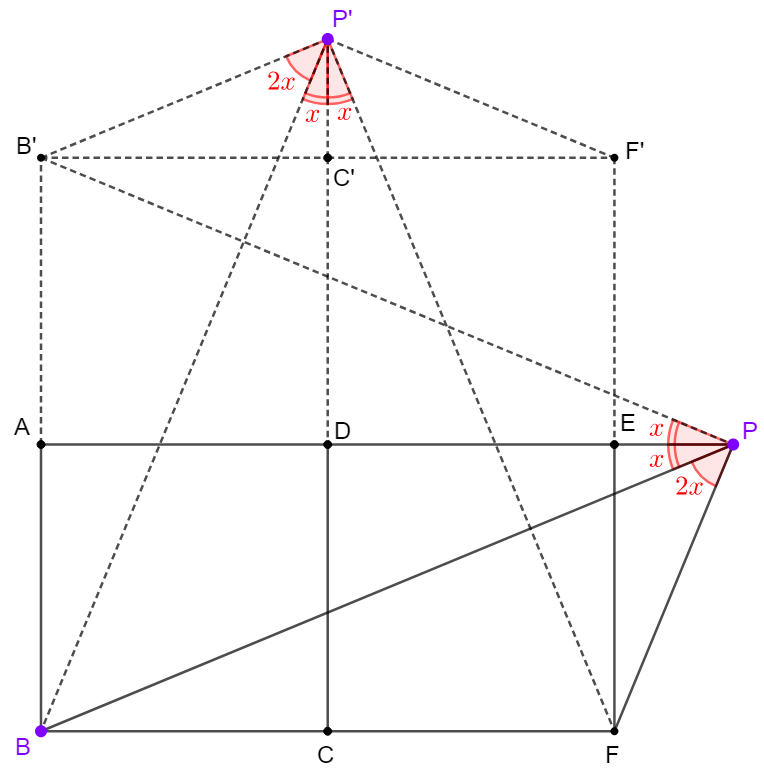
$ABCD$ and $CDEF$ are squares, extend $DE$ to $P$ such that $\angle{BPF}=2\angle{APB}$, find $\angle{APB}$.
Solve:
 \(\begin{multline}
\shoveleft \text{Let }B', C', F' \text{ are reflection points of }B, C, F \text{ about } AE, P'\text{ is reflection point of }P \text{ about }BD\\
\shoveleft \implies \angle{APB'}=\angle{APB}=\angle{BP'C}=\angle{FP'C} \implies \angle{BP'B}=\angle{BPF}=\angle{BPB'}=\angle{BP'F}\\
\shoveleft \implies BB'P'P \text{ is cyclic}, BFPP' \text{ is cyclic} \implies B,P,P' \text{ are shared by two circles}\\
\shoveleft \implies BFPP'B' \text{is cyclic} \implies \angle{BPF}=\angle{BB'F}=45^{\circ}\implies \angle{APB}=\dfrac{45^{\circ}}{2}=\bbox[5px, border: 1px solid black]{22.5^{\circ}}
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Let }B', C', F' \text{ are reflection points of }B, C, F \text{ about } AE, P'\text{ is reflection point of }P \text{ about }BD\\
\shoveleft \implies \angle{APB'}=\angle{APB}=\angle{BP'C}=\angle{FP'C} \implies \angle{BP'B}=\angle{BPF}=\angle{BPB'}=\angle{BP'F}\\
\shoveleft \implies BB'P'P \text{ is cyclic}, BFPP' \text{ is cyclic} \implies B,P,P' \text{ are shared by two circles}\\
\shoveleft \implies BFPP'B' \text{is cyclic} \implies \angle{BPF}=\angle{BB'F}=45^{\circ}\implies \angle{APB}=\dfrac{45^{\circ}}{2}=\bbox[5px, border: 1px solid black]{22.5^{\circ}}
\end{multline}\)
12/30/2023
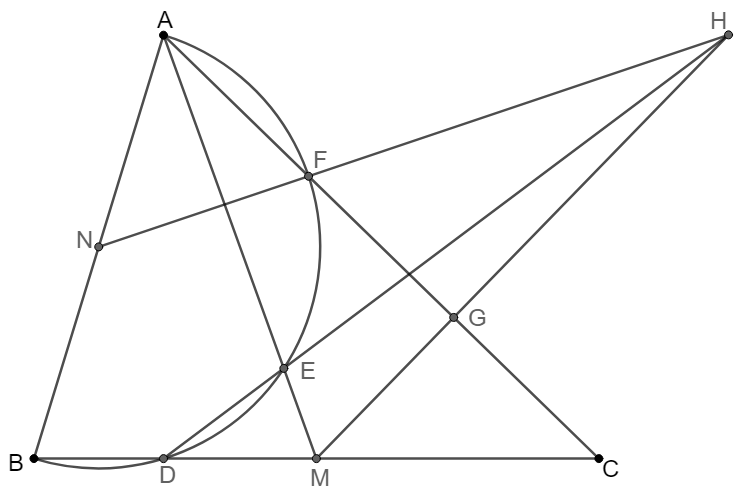
Consider an acute-angled triangle $\triangle{ABC}$ with $|AB|<|AC|$. Let $M$ and $N$ be the midpoints of segments $BC$ and $AC$, respectively. The circle with diameter $\overline{\rm{AB}}$ intersects the lines $BC, AM$ and $ AC $ at $D, E$, and $ F $, respectively. Let $G$ be the midpoint of $\overline{\rm{FC}}$. Prove that the lines $NF, DE$ and $MG$ are concurrent.
Prove:
 \(\begin{multline}
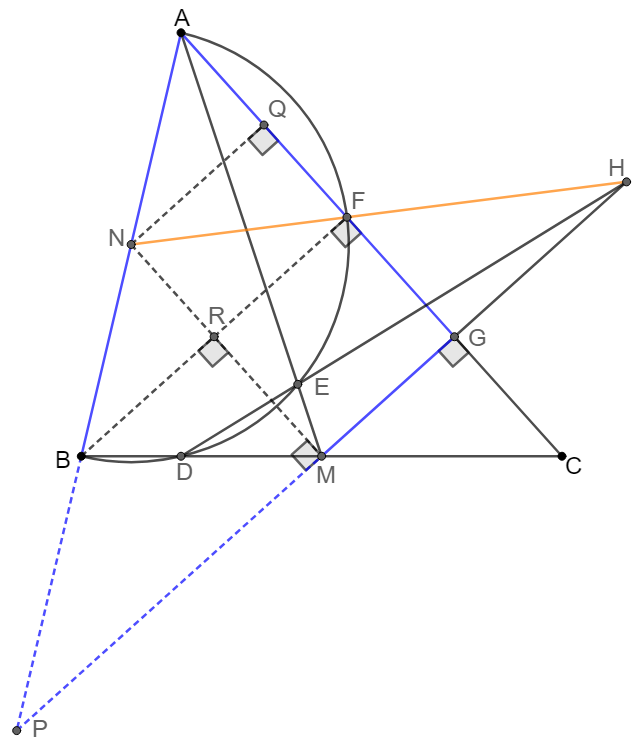
\shoveleft \text{Suppose extended }DE\cap MG=H, \text{now prove } N,F \text{ and }H \text{ are concurrent via Menelaus' Theorem:} \\
\shoveleft \text{Make }NQ\perp AC \text{ at }Q \implies AQ=QF, AN=NB, BM=MC, CG=FG \implies MN \parallel AC, MG \parallel BF\\
\shoveleft AB \text{ is diameter } \implies BF\perp AC \implies BF\perp MN, GM \perp MN, MG \perp AC \implies NG \parallel BF \parallel MG\\
\shoveleft \text{Suppose} BF\cap MN=R, BN=NF\implies \triangle{BRN}\cong\triangle{FRN}\implies \angle{BNR}=\angle{FNR}\\
\shoveleft \text{Let }P \text{ be the intersect of extended } NB \text{ and } GM \implies \triangle{MNH}\cong\triangle{MNP} \implies MH=MP\\
\shoveleft \triangle{HFG}\sim\triangle{HNM}\implies \dfrac{GF}{GH}=\dfrac{MN}{MH}=\dfrac{2MN}{HP}, \triangle{ANQ}\sim\triangle{APM}\implies \dfrac{AN}{NP}=\dfrac{AQ}{MN}=\dfrac{FA}{2MN}\\
\shoveleft \implies \dfrac{GF}{FA}\dfrac{AN}{NP}\dfrac{HP}{GH}=\dfrac{GH}{GH}\dfrac{AN}{NP}\dfrac{HP}{FA}=\dfrac{2MN}{HP}\dfrac{AF}{2MN}\dfrac{HP}{FA}=1\implies N,F \text{ and }H \text{ are concurrent}\blacksquare
\end{multline}\)
\(\begin{multline}
\shoveleft \text{Suppose extended }DE\cap MG=H, \text{now prove } N,F \text{ and }H \text{ are concurrent via Menelaus' Theorem:} \\
\shoveleft \text{Make }NQ\perp AC \text{ at }Q \implies AQ=QF, AN=NB, BM=MC, CG=FG \implies MN \parallel AC, MG \parallel BF\\
\shoveleft AB \text{ is diameter } \implies BF\perp AC \implies BF\perp MN, GM \perp MN, MG \perp AC \implies NG \parallel BF \parallel MG\\
\shoveleft \text{Suppose} BF\cap MN=R, BN=NF\implies \triangle{BRN}\cong\triangle{FRN}\implies \angle{BNR}=\angle{FNR}\\
\shoveleft \text{Let }P \text{ be the intersect of extended } NB \text{ and } GM \implies \triangle{MNH}\cong\triangle{MNP} \implies MH=MP\\
\shoveleft \triangle{HFG}\sim\triangle{HNM}\implies \dfrac{GF}{GH}=\dfrac{MN}{MH}=\dfrac{2MN}{HP}, \triangle{ANQ}\sim\triangle{APM}\implies \dfrac{AN}{NP}=\dfrac{AQ}{MN}=\dfrac{FA}{2MN}\\
\shoveleft \implies \dfrac{GF}{FA}\dfrac{AN}{NP}\dfrac{HP}{GH}=\dfrac{GH}{GH}\dfrac{AN}{NP}\dfrac{HP}{FA}=\dfrac{2MN}{HP}\dfrac{AF}{2MN}\dfrac{HP}{FA}=1\implies N,F \text{ and }H \text{ are concurrent}\blacksquare
\end{multline}\)