M∀TH Workout

September 2023

 
  • Sep 01, 2023

09/01/2023

$D, E$ is on side $BC, AC$ of equilateral $\triangle{ABC}$ such that $\angle{ADB}=2\angle{EDC}$. Prove that $AD=BD+CE$.

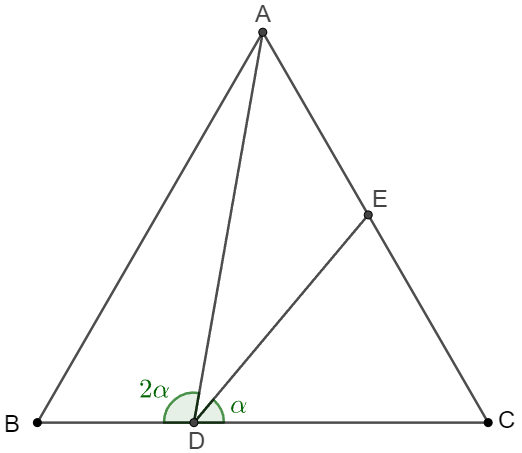
image-20230901130602876

Prove 1:

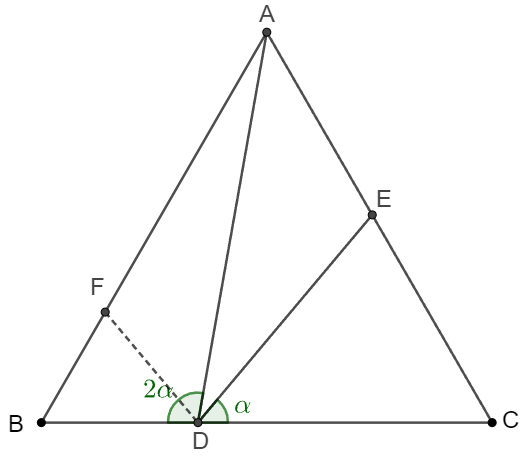image-20230901130700387 \(\begin{multline}\nonumber \shoveleft \text{Let } F \text{ on side } AB \text{ such that } DF \text{ bisects } \angle{ADB}.\\ \shoveleft \text{Let }AB=BC=CA=d, AD=a, BD=b, CD=d-b, CE=c\\ \shoveleft DF \text{ bisects }\angle{ADB} \implies \dfrac{a}{AF}=\dfrac{b}{BF}\\ \shoveleft \angle{CDE}=\angle{BDF}, \angle{DBF}=\angle{DCE}\implies \triangle{DBF} \sim \triangle{CDE}\\ \shoveleft \implies \dfrac{c}{BF}=\dfrac{d-b}{b} \implies BF=\dfrac{bc}{d-b}, AF=\dfrac{ac}{d-b}\\ \shoveleft \implies AB=d=\dfrac{(a+b)c}{d-b} \implies d(d-b)=(a+b)c\\ \shoveleft cos(\angle{ABD})=\dfrac{d^2+b^2-a^2}{2bd}=cos(60^{\circ})=\dfrac{1}{2} \implies d^2 + b^2 - a^2 = bd\\ \shoveleft \implies (a+b)(a-b)=d(d-b) = (a+b)c \implies a=b+c \implies AD=BD+CE \blacksquare \end{multline}\) Prove 2:

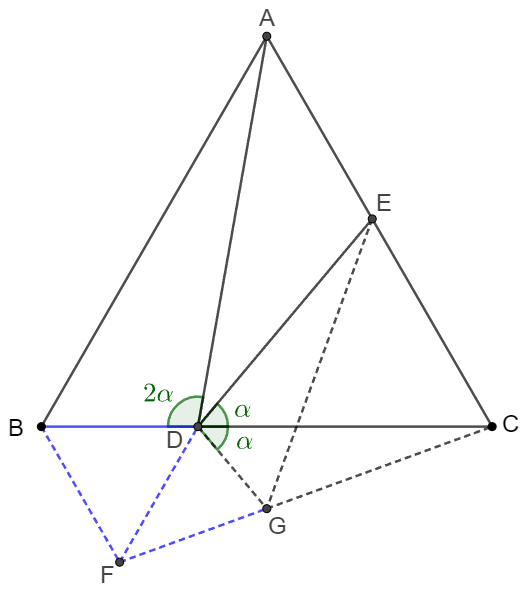image-20230902113649928 \(\begin{multline}\nonumber \shoveleft \text{Rotate } \triangle{ABD} \text{ 60 degrees clockwise around } B \text{ to get } \triangle{CBF}\\ \shoveleft \text{Let } G \text{ on } CF \text{ such that }\angle{CDG}=\alpha, \text{connect } DG, EG\\ \shoveleft \implies \angle{BFC=2\alpha}, CF=AD, \triangle{BDF} \text{ is equilateral} \implies BD=BF=DF\\ \shoveleft \implies \angle{DFG}=2\alpha-60^{\circ}, \angle{FDG}=120^{\circ}-\alpha \\ \shoveleft \implies \angle{FGD}=\angle{FDG}=180^{\circ}-(60^{\circ}+\alpha)=\angle{DEC}\\ \shoveleft \implies BD=DF=FG, CEDG \text{ is cyclic}\\ \shoveleft \implies \angle{CGE}=\angle{CDE}=\alpha, \angle{CEG}=\angle{CDG}=\alpha\\ \shoveleft \implies CE=CG \implies CF=GF+CG=BD+CE=AD\blacksquare\\ \end{multline}\) Prove 3:

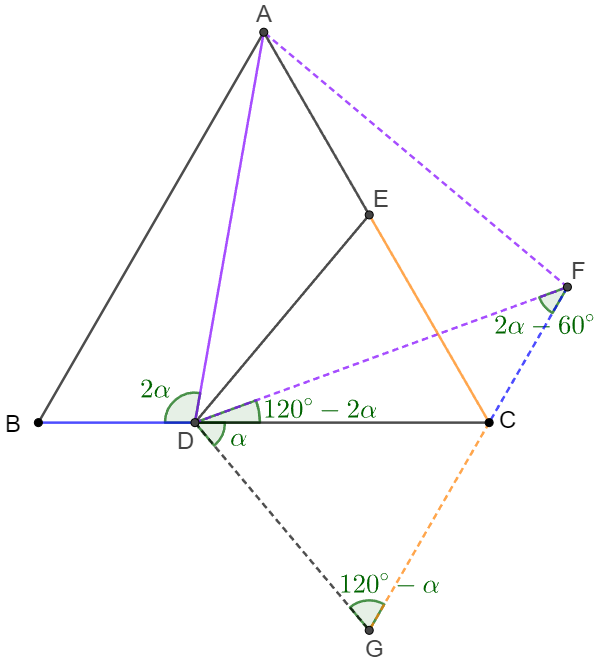image-20230902120848800 \(\begin{multline}\nonumber \shoveleft \text{Rotate } \triangle{ABD} \text{ 60 degrees counter-clockwise around } A \text{ to get } \triangle{ACF}\\ \shoveleft \text{Extend } FC \text{ to } G \text{ such that } \angle{CDG}=\alpha \implies \triangle{ADF} \text{ is equilateral}\\ \shoveleft BD=CF, \angle{FDC}=120^{\circ}-2\alpha,\angle{DCG}=60^{\circ} \implies CG=CE,\angle{FGD}=120^{\circ}-\alpha\\ \shoveleft \implies \angle{FGD}=\angle{FDG} \implies AD=FD=FG \implies FG=AD=BD+CE\blacksquare \end{multline}\)

09/10/2023

In trapezoid $ABCD$,$BC \parallel AD$, $M, N$ are two points inside it such that $AM \parallel CN, BN \parallel DM$. Prove that $[ABN]=[CDM]$.

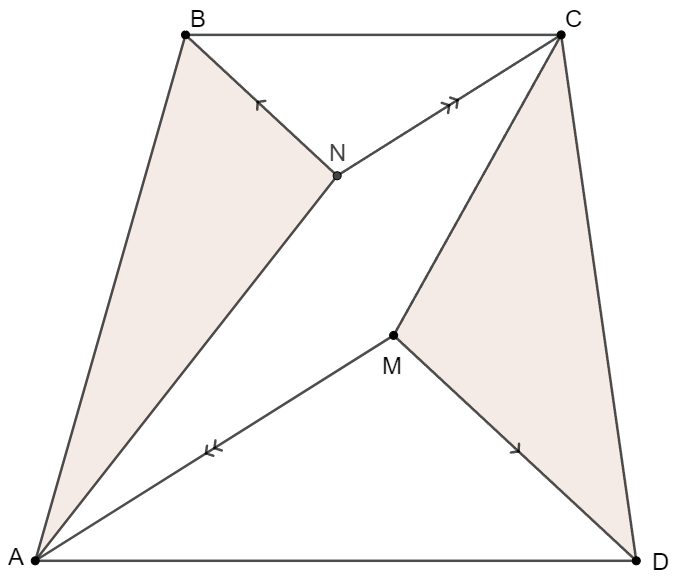
image-20230910171142140

Prove:

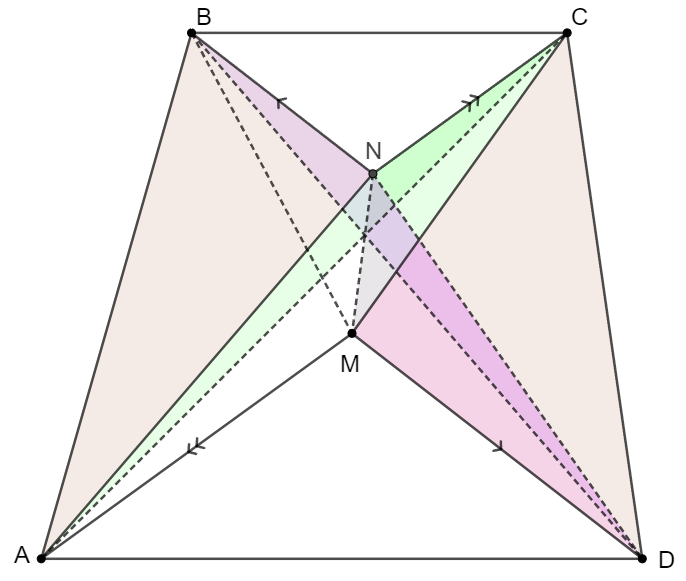image-20230910173458519 \(\begin{multline}\nonumber \shoveleft [ABN]=[ABC]-[ACN]-[BCN], [ABC]=[DBC], [ACN]=[MCN]\\ \shoveleft \implies [ABN]=[DBC]-[MCN]-[BCN]=[BDN]+[DCN]-[MCN]\\ \shoveleft [BDN]=[MDN] \implies [ABN]=[MDN]+[DCN]-[MCN]\\ \shoveleft =[CDMN]-[MCN]=[MCN]+[CDM]-[MCN]=[CDM]\blacksquare \end{multline}\)

09/11/2023

$D, E$ are points on side $AC, BC$ in right-angle $\triangle{ABC}$ such that $\angle{BDE}=90^{\circ}, \angle{DBE}=\angle{CDE}, [ABD]=[CDE]=1$, find $[BDE]$.

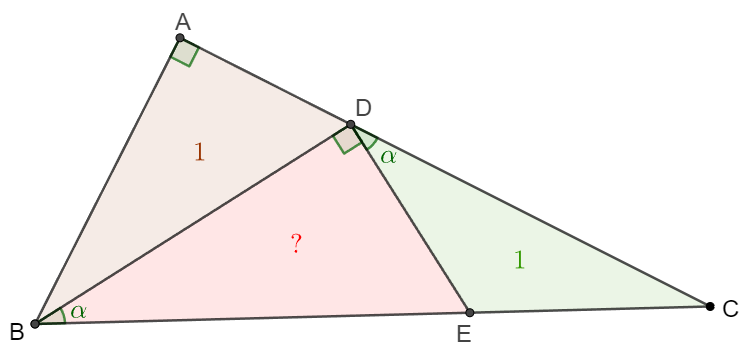
image-20230911045009257

Solve:

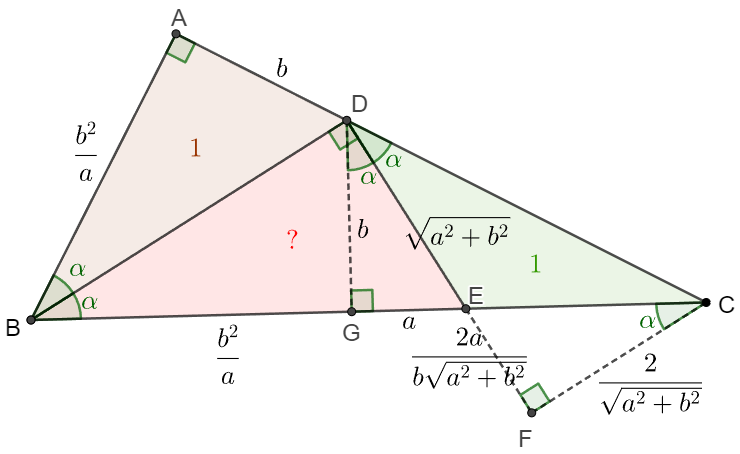image-20230911050905435 \(\begin{multline}\nonumber \shoveleft \text{Let } G \text{ on } BC \text{ such that } DG\perp BC, F \text{ on extended } DE \text{ such that } DF \perp CF\\ \shoveleft \implies \angle{GDE}=\angle{DBE}=\angle{ABD}=\angle{CDE}=\angle{ECF}=\angle{\alpha}\\ \shoveleft \text{Let } GE=a, DG=b, [ABD]=[CDE]=1\implies\\ \shoveleft b^3=2a,AD=GD=b, AB=GB=\dfrac{b^2}{a}, DE=\sqrt{a^2+b^2}, CF=\dfrac{2}{\sqrt{a^2+b^2}}\\ \shoveleft \implies \dfrac{DG}{GE}=\dfrac{DE+EF}{CF}\implies \dfrac{b}{a}=\dfrac{\sqrt{a^2+b^2}+\dfrac{2a}{b\sqrt{a^2+b^2}}}{\dfrac{2}{\sqrt{a^2+b^2}}} \implies\\ \shoveleft a^3+ab^2+\dfrac{2a^2}{b}=2b \implies a^3b^3+ab^5+2a^2b^2=2b^4\implies (ab)^3+2a^2b^2+2a^2b^2=4ab\\ \shoveleft \implies (ab)^2+4ab=4 \implies ab=\sqrt{2}-1\implies [BDE]=1+ab=\bbox[5px, border: 1px solid black]{\displaystyle \sqrt{2}} \end{multline}\) Solve 2: \(\begin{multline}\nonumber \shoveleft \text{Let } G \text{ on } BC \text{ such that } DG\perp BC, [DGE]=x \implies\\ \shoveleft \angle{GDE}=\angle{DBE}=\angle{ABD}=\angle{CDE}=\angle{ECF}=\angle{\alpha}\implies\\ \shoveleft AD=DG,\dfrac{[BCD]}{[ABD]}=\dfrac{2+x}{1}=\dfrac{CD}{AD}=\dfrac{CD}{DG}=\dfrac{CE}{GE}=\dfrac{[CDE]}{[GDE]}=\dfrac{1}{x}\\ \shoveleft \implies x^2+2x-1=0\implies x=\sqrt{2}-1\implies [BDE]=\bbox[5px, border: 1px solid black]{\sqrt{2}} \end{multline}\)

09/12/2023

$D,E$ are points on side $AB, AC$ of $\triangle{ABC}$ such that $\dfrac{BD}{AC}=\dfrac{CE}{AB}=\dfrac{DE}{BC}$. Prove that the circumcenter $O$ of $\triangle{ABC}$ is on the circumcircle of $\triangle{ADE}$.

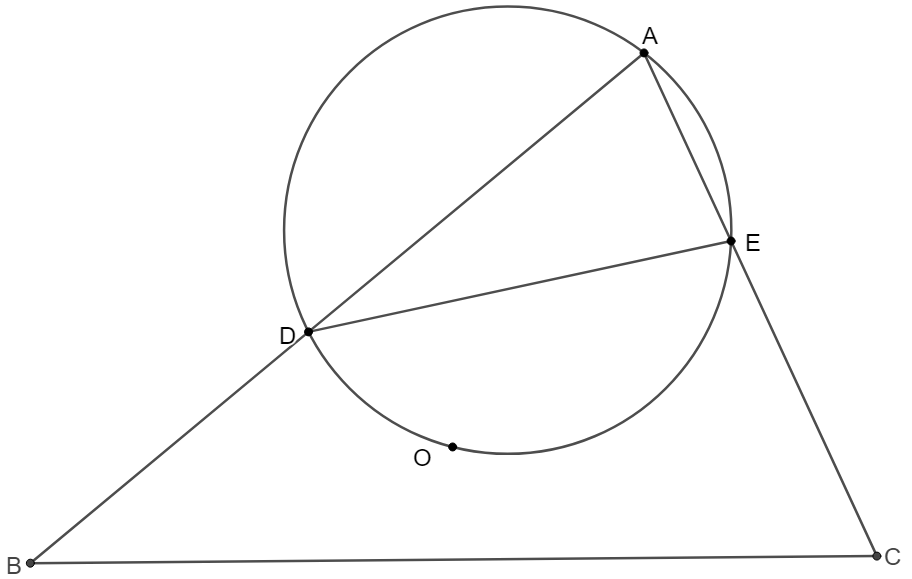
image-20230912132853546

Prove:

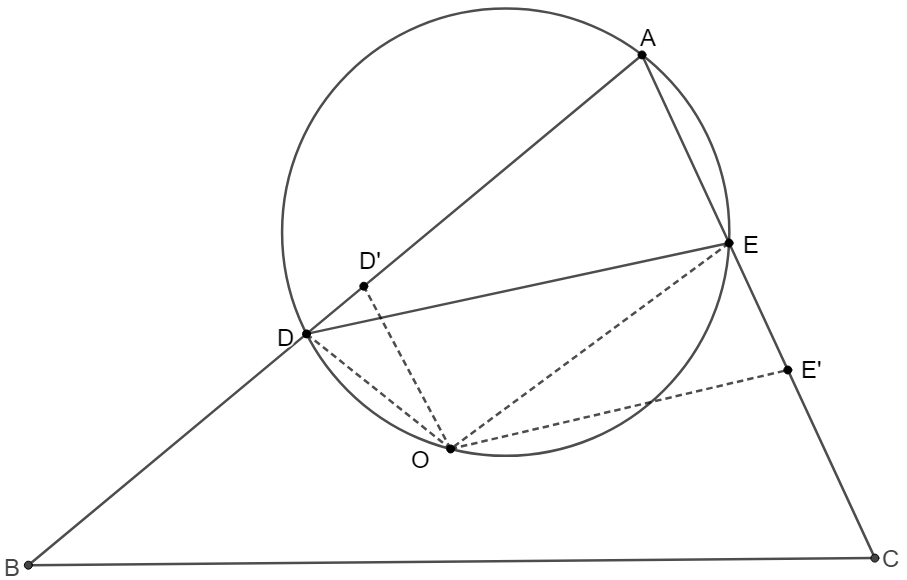image-20230912133010484 \(\begin{multline}\nonumber \shoveleft \text{Make } B', C' \text{ on side } AD, AE \text{ such that }AB'=BD, AD=C'E\\ \shoveleft \implies \dfrac{AC}{AD'}=\dfrac{AC}{BD}=\dfrac{AB}{CE}=\dfrac{AB}{AE'}\implies \triangle{AD'E'}\sim\triangle{ABC}\\ \shoveleft \implies \dfrac{D'E'}{BC}=\dfrac{AD'}{AC}=\dfrac{BD}{AC}=\dfrac{DE}{BC} \implies DE=D'E'\\ \shoveleft O \text{is on perpendicular sector of }AB, AC \implies OD=OD', OE=OE'\\ \shoveleft \implies \triangle{ODE}\cong\triangle{OD'E'}\implies \triangle{ODD'}\sim\triangle{OEE'}\\ \shoveleft \implies \angle{CD'D}=\angle{OE'E}\implies ADOE \text{ is cyclic}\\ \shoveleft \implies O \text{ is on circumcircle of }\triangle{ADE}\blacksquare \end{multline}\)

09/17/2023

Point $D$ is inside $\triangle{ABC}$ such that $\angle{BAD}=10^{\circ}, \angle{CAD}=20^{\circ}, \angle{ABD}=40^{\circ}, \angle{CBD}=30^{\circ}$, find $\angle{ACD}$

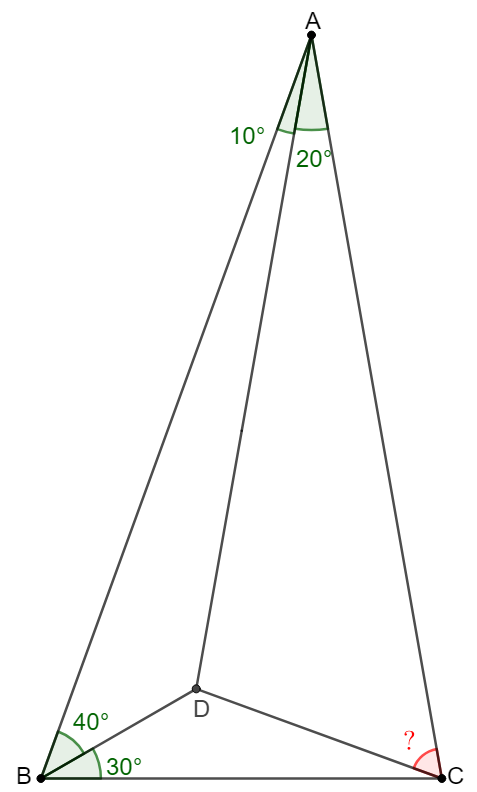
image-20230917202102710

Solve:

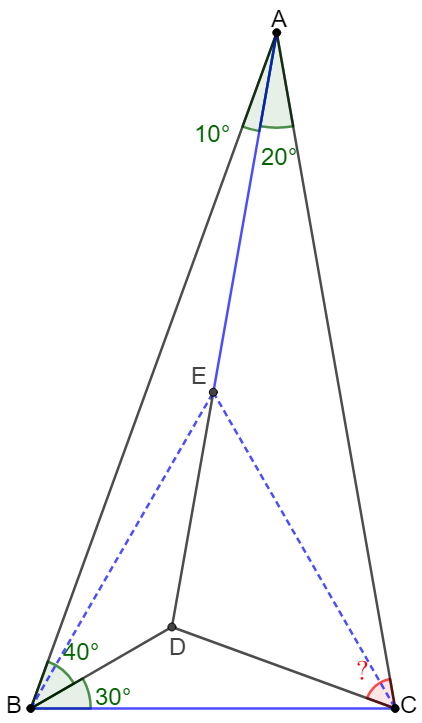image-20230917200613201 \(\begin{multline}\nonumber \shoveleft \text{ Let point } E \text{ on } AD \text{ such that } \angle{EBD}=30^{\circ} \\ \shoveleft \implies \angle{EBA}=\angle{EAB}=10^{\circ}\\ \shoveleft \implies \angle{AEB}=160^{\circ}=2\angle{ACB}, BE=AE\\ \shoveleft \implies E \text{ is circumcenter of } \triangle{ABC}\\ \shoveleft \implies AE=BE=CE, \angle{ACE}=\angle{CAE}=20^{\circ}\\ \shoveleft \implies \triangle{BCE} \text{ is euqilateral}\\ \shoveleft \implies CD=DE \implies \angle{DCE}=\angle{DEC}=40^{\circ}\\ \shoveleft \implies ACD=40^{\circ}+20^{\circ}=\bbox[5px, border: 1px solid black]{60^{\circ}} \end{multline}\)

09/18/2023

Point $D$ is on side $BC$ of $\triangle{ABC}$ such that $AB=CD$, and $\angle{ABC}=40^{\circ}, \angle{BAD}=60^{\circ}$, find $\angle{ACB}$.

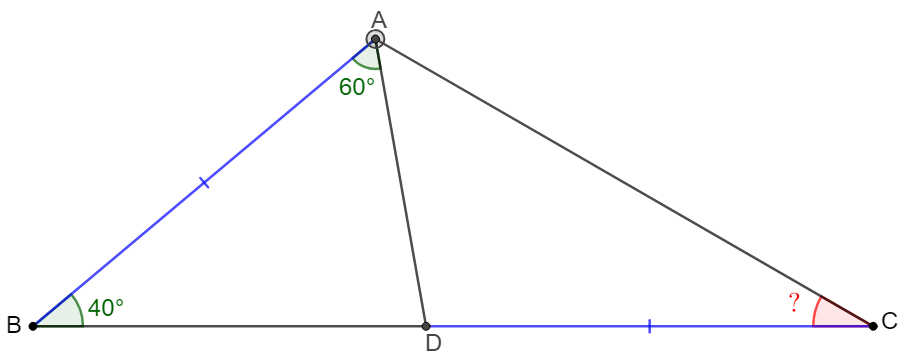
image-20230918045716542

Solve:

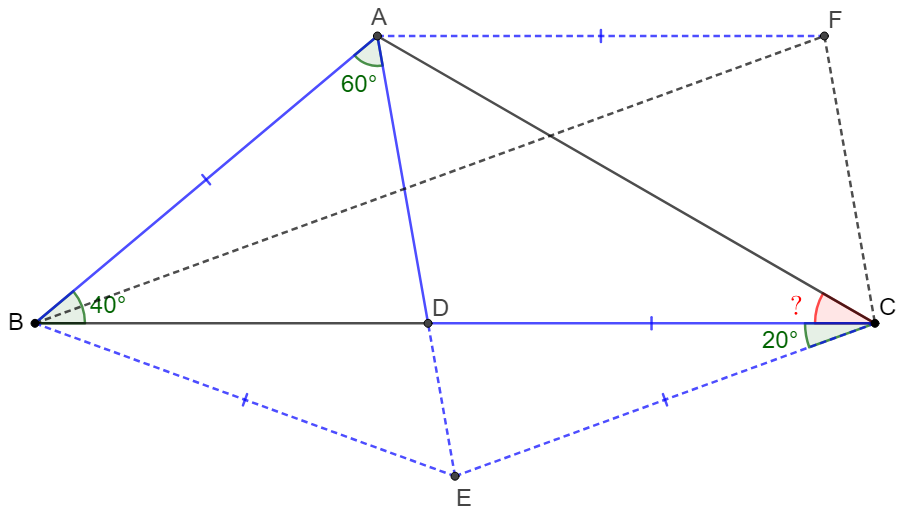image-20230918114752768 \(\begin{multline}\nonumber \shoveleft \text{Make parallelogram } ADCF, \text{ connect } BF. \\ \shoveleft AB=CD=AF \implies \angle{ABF}=\angle{AFB}=\angle{FBC}\\ \shoveleft \implies \angle{ABF}=\angle{AFB}=\angle{FBC}=20^{\circ}\\ \shoveleft \angle{ADB}=80^{\circ}=\angle{FCB}=\angle{BFC} \implies BF=BC\\ \shoveleft \text{Extend }AD \text{ to } E \text{ such that } \angle{BCE}=20^{\circ}\\ \shoveleft \implies \angle{CDE}=\angle{CED}=80^{\circ} \implies CD=CE=AF\\ \shoveleft \implies \triangle{ABF}\cong \triangle{EBC} \implies BE=AB, \angle{EBC}=20^{\circ}\\ \shoveleft \implies \triangle{ABE} \text{ is equilateral} \implies E \text{ is circumcenter of } \triangle{ABC}\\ \shoveleft \implies \angle{ACB}=\dfrac{\angle{AEB}}{2}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

09/19/2023

$BE$ is perpendicular bisector of $AC$. $\angle{ADE}=\angle{ADC}=60^{\circ}$. Show that $AC=AE$.

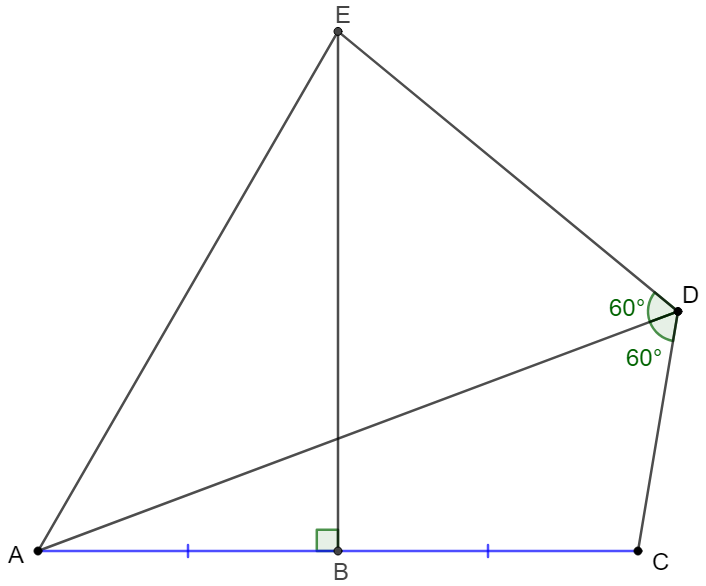
image-20230919124505563

Prove:

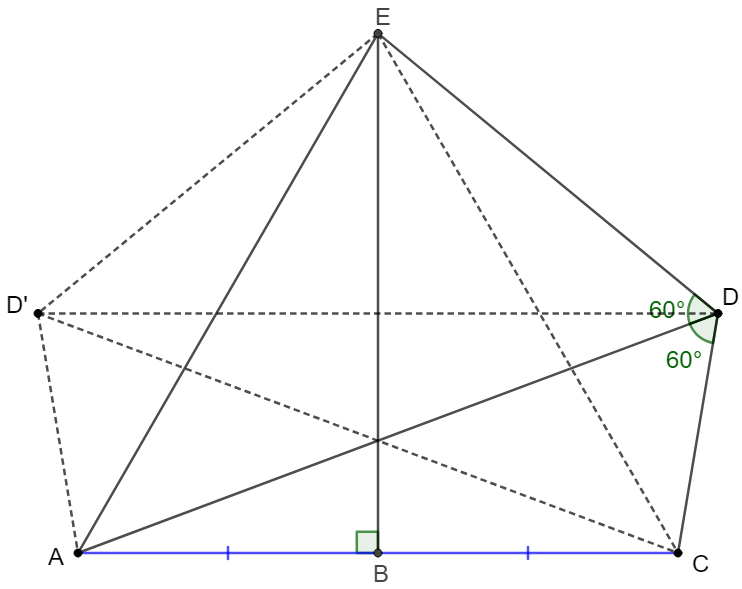image-20230919131520487 \(\begin{multline}\nonumber \shoveleft \text{Make } D' \text{to be the mirror point of } D \text{ about BE} \implies\\ \shoveleft \angle{AD'C}=\angle{ADC}=\angle{CD'E}=\angle{ADE}=60^{\circ} \implies \\ \shoveleft ACDD' \text{ is cyclic}, \angle{CD'E}+\angle{CDE}=180^{\circ} \implies\\ \shoveleft CDED' \text{ is cyclic} \implies ACDED' \text{ is cyclic} \implies \\ \shoveleft \angle{AEC}=\angle{ADC}=60^{\circ} \implies \triangle{ACE} \text{ is equilateral}\\ \shoveleft \implies AE=AC \blacksquare \end{multline}\)

09/20/2023

$D$ is a point on the circumcircle of equilateral triangle $\triangle{ABC}$. $E, F$ are midpoints of $BC, AD$. Show that $DE=EF$ .

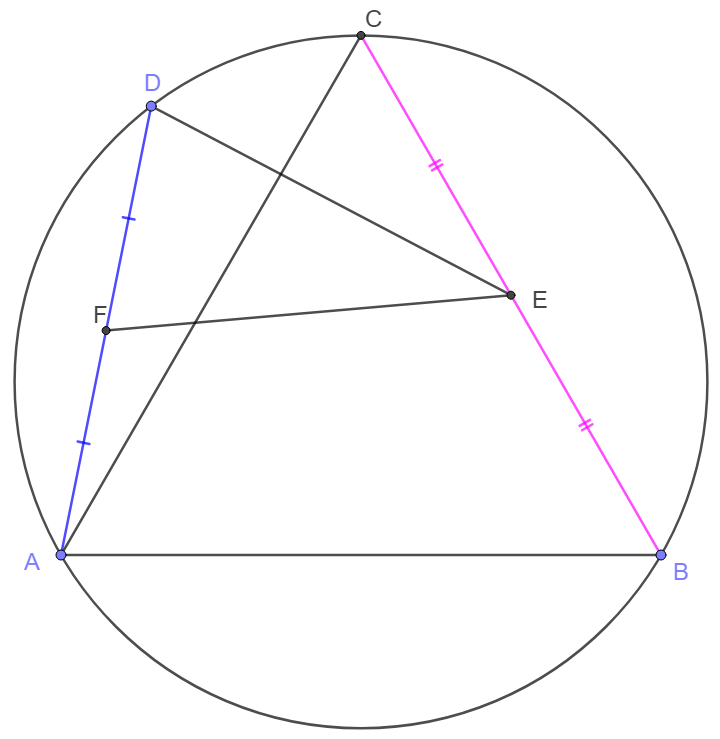
image-20230919230435696

Prove:

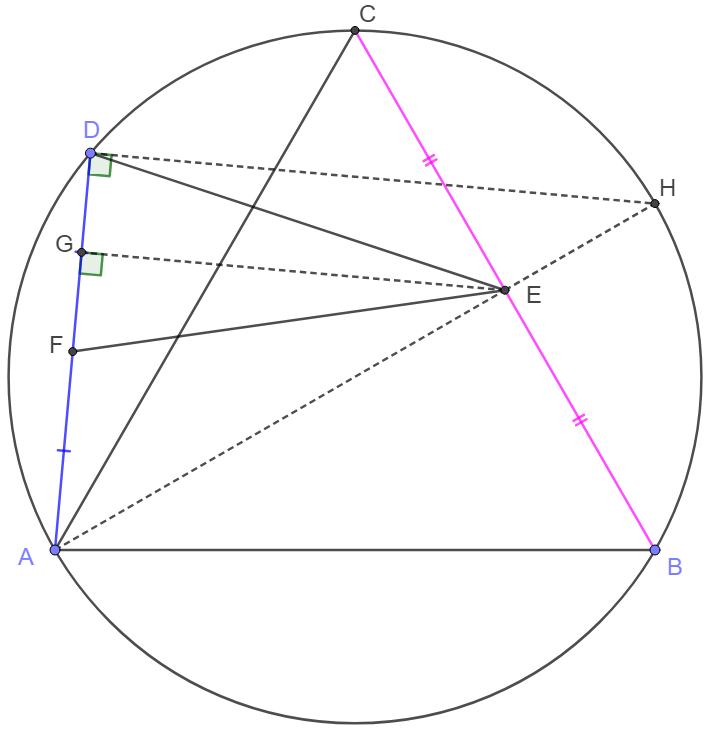image-20230919231135690 \(\begin{multline}\nonumber \shoveleft \text{Let } G \text{ on } DF \text{ such that } EG\perp DF, H \text{ on the circumcicle and extended } AE, \text{ connect }EG, DH.\\ \shoveleft \implies AD\perp DH, \dfrac{EH}{AE}=\dfrac{AH-AE}{AE}=\dfrac{AH}{AE}-1=\dfrac{\dfrac{2}{\sqrt{3}}BC}{\dfrac{\sqrt{3}}{2}BC}-1=\dfrac{1}{3}\\ \shoveleft \implies \dfrac{DG}{AG}=\dfrac{1}{3} \implies DG=GF\implies DE=EF\blacksquare \end{multline}\)

09/21/2023

$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=20^{\circ}, \angle{BCD}=\angle{CBD}=10^{\circ}, \angle{ACD}=100^{\circ}$, find $\angle{CAD}$.

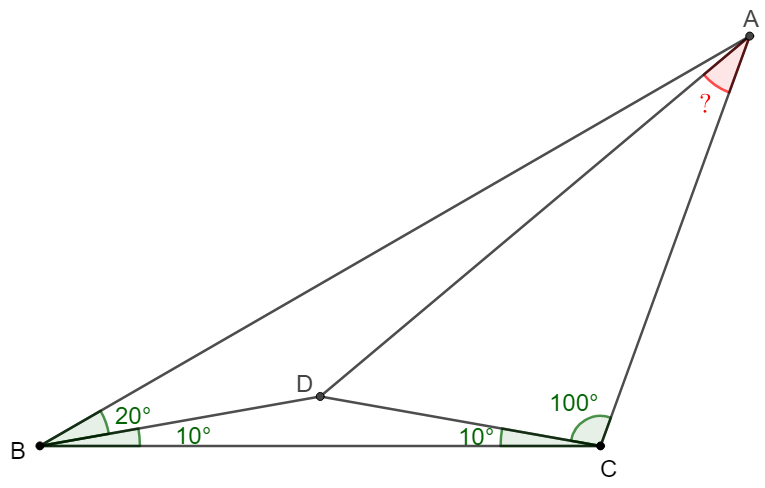
image-20230922001117386

Solve:

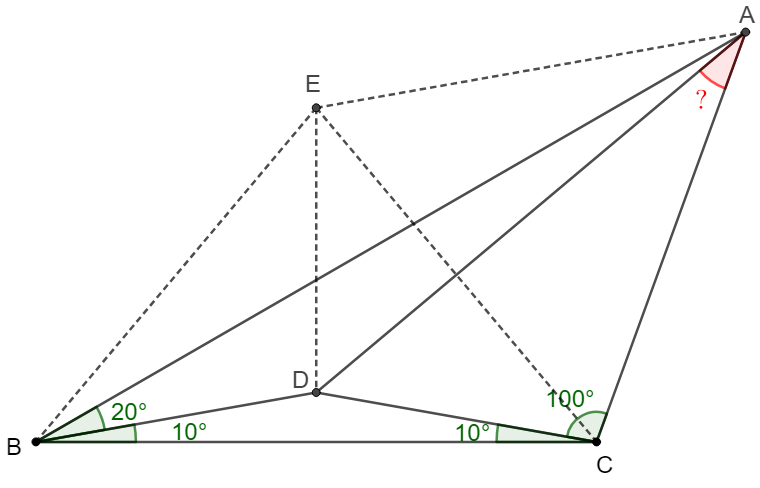image-20230922000101974 \(\begin{multline}\nonumber \shoveleft \text{Make } E \text{ be the circumcenter of } \triangle{ABC} \implies \\ \shoveleft AE=BE=CE, \angle{AEC}=60^{\circ}, \angle{BEC}=80^{\circ}\\ \shoveleft \implies \triangle{ACE} \text{ is equilateral}, \triangle{BDE}\cong\triangle{CDE}\\ \shoveleft \implies \angle{CED}=40^{\circ}=\angle{DCE}\implies CD=DE\\ \shoveleft \implies \triangle{ADE}\cong\triangle{ADC}\implies \angle{CAD}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

09/22/2023

$D$ is on side $BC$ in $\triangle{ABC}$, and $AD\perp BC, \angle{ACD}=40^{\circ}$. $E$ is a point on $AD$ such that $\angle{ABE}=20^{\circ}, \angle{EBD}=10^{\circ}$. Find $\angle{DCE}$.

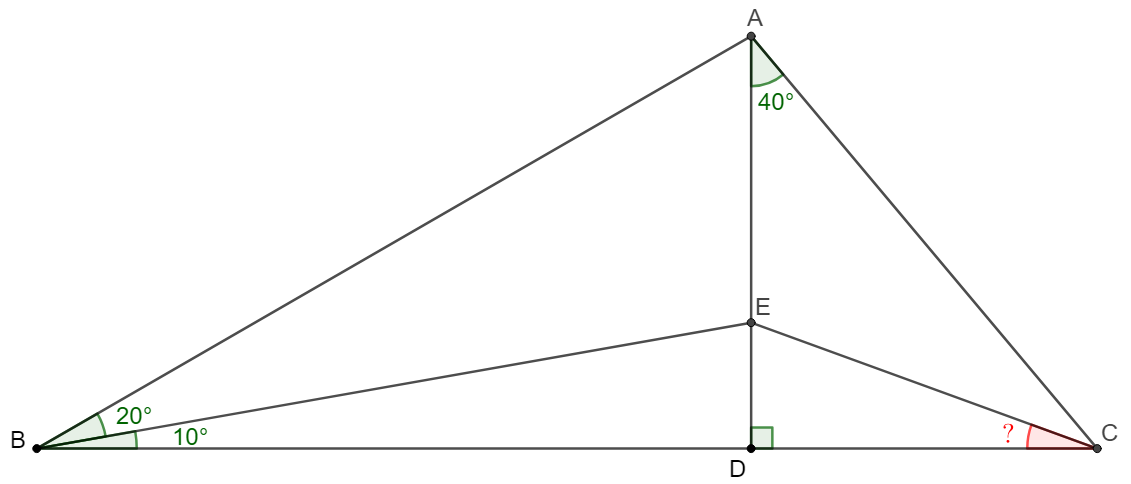
image-20230922002146883

Solve:

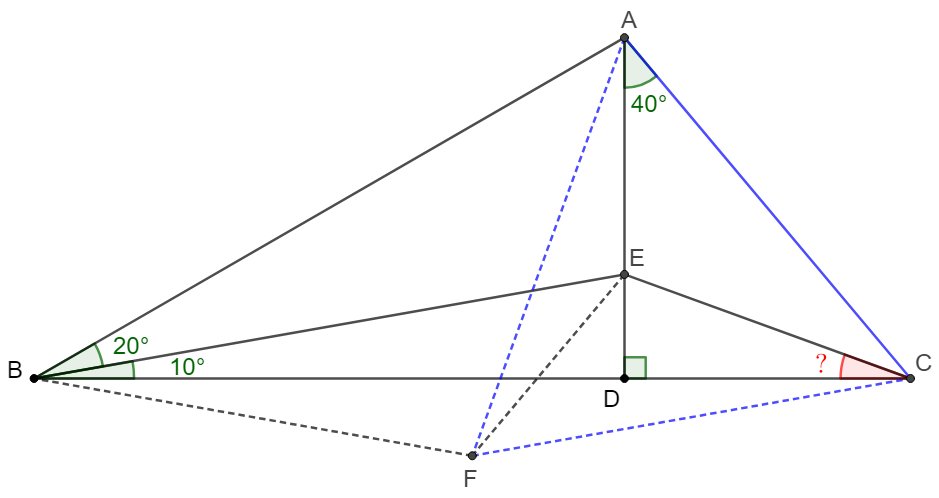image-20230922005059434 \(\begin{multline}\nonumber \shoveleft \text{Make } \triangle{ACF} \text{ an equilateral triangle such that } F \text{ is below } BC.\\ \shoveleft \implies AF=CF=AC, \angle{AFC}=60^{\circ}=2\angle{ABC}\\ \shoveleft \implies F \text{ is circumcenter of } \triangle{ABC} \implies BF=CF=AF\\ \shoveleft \implies \angle{FBC}=\angle{FCB}=10^{\circ} \implies \angle{BAF}=\angle{ABF}=40^{\circ}\\ \shoveleft \implies \angle{EAF}=\angle{EAB}-40^{\circ}=60^{\circ}-20^{\circ}=\angle{EBF}\\ \shoveleft \implies ABFE \text{ is cyclic }\implies \angle{AFE}=\angle{ABE}=20^{\circ}=\angle{EAF}\\ \shoveleft \implies AE=EF\implies \triangle{ACE}\cong \triangle{FCE}\implies \angle{ACE}=\angle{FCE}=30^{\circ}\\ \shoveleft \implies \angle{DCE}=\angle{FCE}-\angle{FCB}=30^{\circ}-10^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}} \end{multline}\)

09/23/2023

In $\triangle{ABC}$, $\angle{A}=60^{\circ}, a+b=2c$, show that $a=b=c$.

Prove:

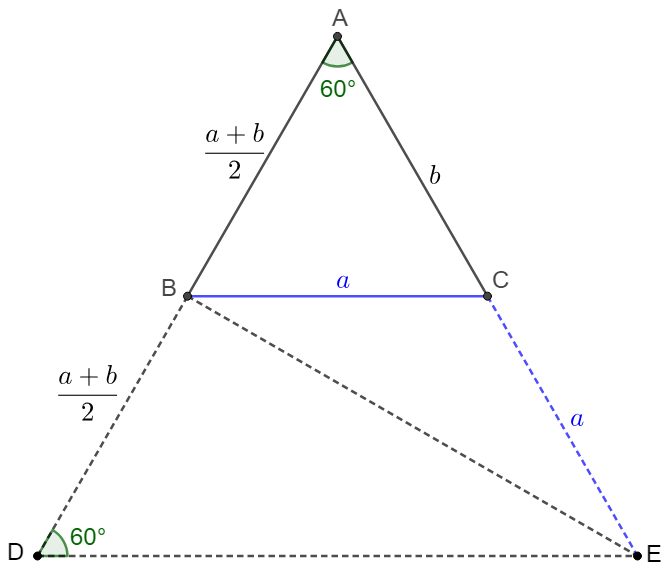image-20230925055756591 \(\begin{multline}\nonumber \shoveleft \text{Extend } AB \text{ to } D \text{ such that } BD=AB=c=\dfrac{a+b}{2}\\ \shoveleft \text{Extend } AC \text{ to } E \text{ such that } CE=BC=a \implies\\ \shoveleft AD=AE=a+b, \angle{A}=60^{\circ} \implies ADE \text{ is equilateral}\\ \shoveleft \implies AE=DE, AB=BD \implies \triangle{ABE}\cong \triangle{DBE}\\ \shoveleft \implies \angle{CEB}=30^{\circ}=\angle{CBE}\implies \angle{ACB}=60^{\circ}\\ \shoveleft \implies \triangle{ABC} \text{ is equilateral} \implies a=b=c\blacksquare \end{multline}\)

09/24/2023

Four lines intersect at six points $A,B,C,D,E,F$ and $G,H,M$ is the midpoint of diagonal $EF, AC, BD$ respectively. Show that $G,H,M$ are collinear. (Line $GHM$ is called Newton-Gauss Line)

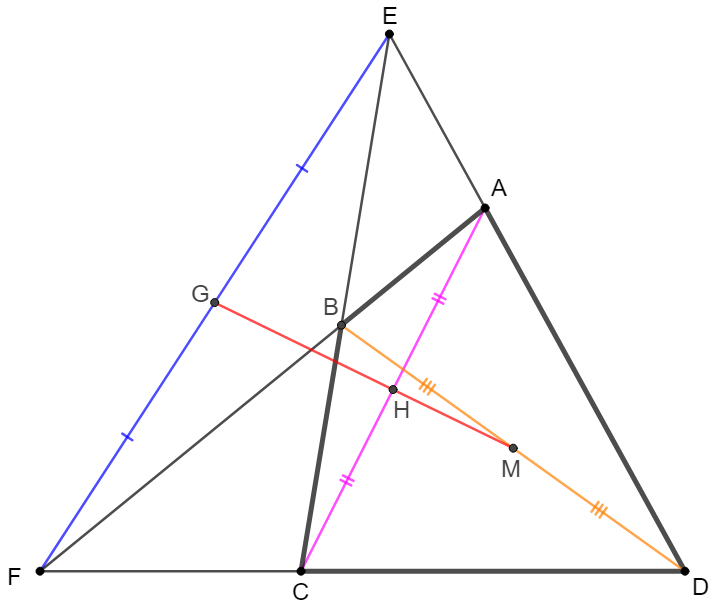
image-20230925113452019

Prove:

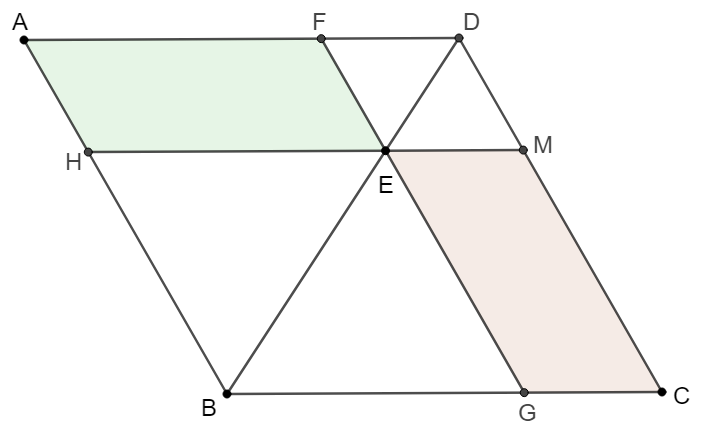
image-20230925121227375

Theorem (Euclid, I, 43): $E$ is a point on the diagonal $BD$ of parallelogram $ABCD$. Make parallel lines to the sides of $ABCD$ through point $E$, then the areas of two small parallelograms are equal: $[AFEH]=[EMCG]$, and conversely.

Prove 1: \(\begin{multline}\nonumber \shoveleft E \text{ is on diagonal of parallem } ABCD, GF \parallel BC \parallel AD, HM \parallel AB \parallel CD\\ \shoveleft \implies \dfrac{EF}{EM}=\dfrac{BH}{BG} \implies \dfrac{EF}{BH}=\dfrac{EM}{BG}, \dfrac{[AFEH]}{[HEGB]}=\dfrac{EF}{BH}, \dfrac{[EMCG]}{[HEGB]}=\dfrac{EM}{BG}\\ \shoveleft \implies [AFEH]=[EMCG], \text{conversely will be the same. }\blacksquare\\ \shoveleft \text{Conversely, if }[AFEH]=[EMCG], GF \parallel BC \parallel AD, HM \parallel AB \parallel CD\\ \shoveleft \implies \dfrac{[AFEH]}{[HEGB]}=\dfrac{EF}{BH}, \dfrac{[EMCG]}{[HEGB]}=\dfrac{EM}{BG} \implies \dfrac{EF}{FD}=\dfrac{BH}{HE}=\dfrac{AB}{AD}\\ \shoveleft \implies \triangle{DEF} \sim \triangle{DBA} \implies \angle{FDE}=\angle{ADB} \implies E \text{ is on } BD\blacksquare\\ \shoveleft \end{multline}\)

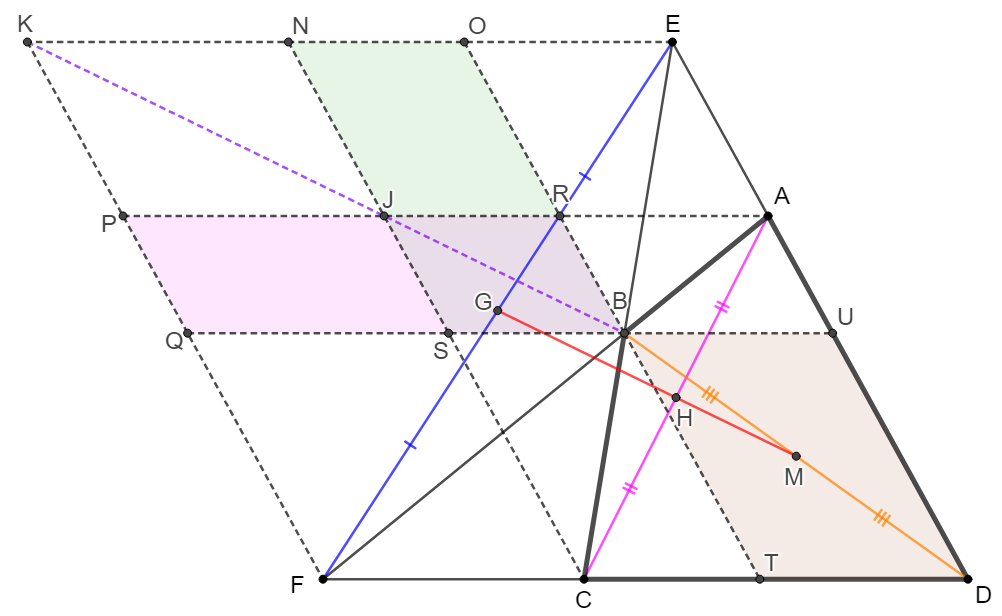image-20230925120052406 . \(\begin{multline}\nonumber \shoveleft \text{Make lines parallel to the sides of } AD, CD. \text{ Applying the theorem: }\\ \shoveleft \text{In }PADF: [PRBQ]=[BUDT]. \text{In }NEDC: [NOBS]=[BUDT]\\ \shoveleft \implies [NOBS]=[PRBQ] \implies J \text{ is on diagonal }KB \text{ in }KOBQ\\ \shoveleft \implies K,J,B \text{ are collinear} \implies \text{the midpoints of }KD, JD, BD \text{ are collinear}\\ \shoveleft \text{Since }AC, DJ \text{ bisect each other}, KD, EF \text{ bisect each other} \implies\\ \shoveleft \text{midpoints of }BD, AC, EF \text{, i.e., } G,H,M \text{ are collinear} \blacksquare \end{multline}\)

Prove 2:

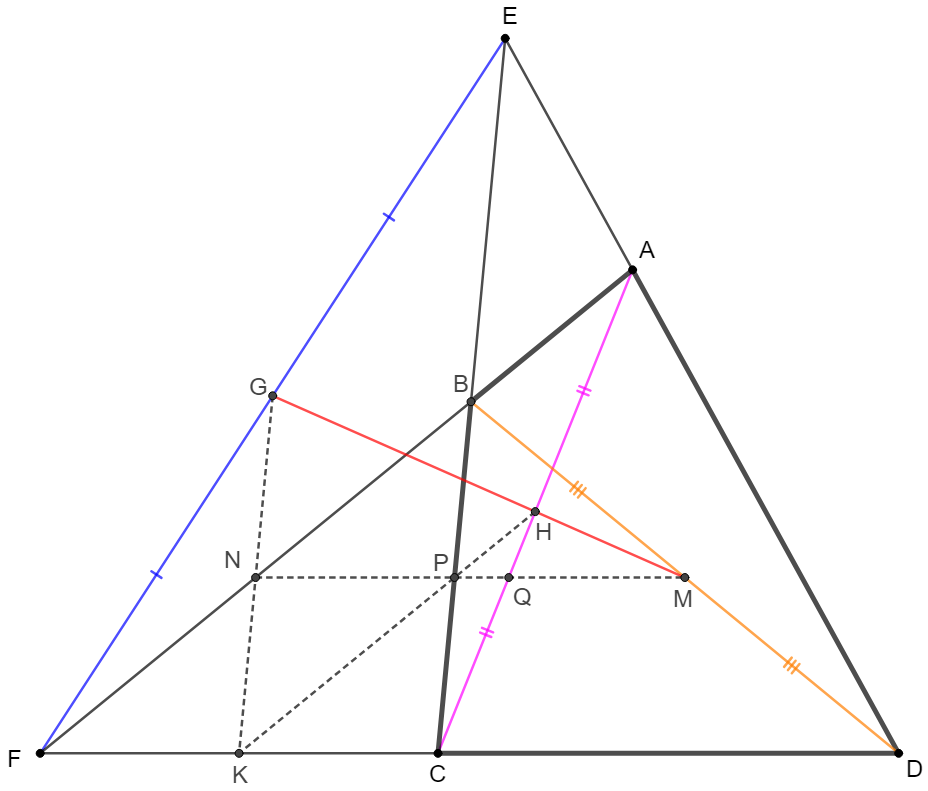image-20230925170554127 \(\begin{multline}\nonumber \shoveleft \text{Let }K, N, P \text{ be the midpoint of } FC, CB, BC \text{ respectively.}\\ \shoveleft \implies KN \cap EF= G, KP \cap AC = H, NP \cap BD = M\\ \shoveleft \implies \dfrac{MN}{PM}=\dfrac{FD}{CD}, \dfrac{HP}{HK}=\dfrac{AB}{AF}, \dfrac{GK}{GN}=\dfrac{EC}{EB}\\ \shoveleft EAD \text{ is a transversal cutting of the sides of } \triangle{FBC}\\ \shoveleft \implies \dfrac{EC}{EB} \dfrac{AB}{AF} \dfrac{FD}{CD} = 1 \implies \dfrac{GK}{GN}\dfrac{HP}{HK}\dfrac{MN}{PM}=1\\ \shoveleft \implies GHM \text{ is a transversal cutting of the side of } \triangle{NPK}\\ \shoveleft \implies G, H, M \text{ is collinear} \blacksquare \end{multline}\)

Prove 3:

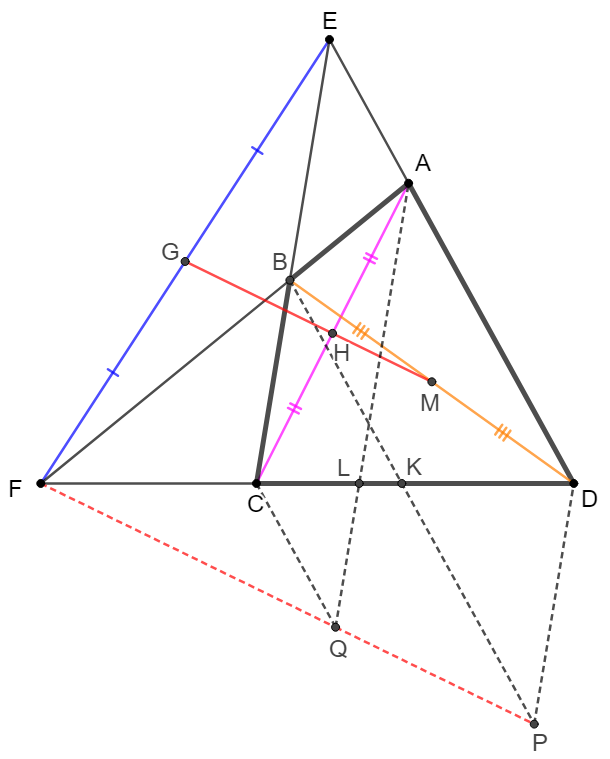image-20230927001104650 \(\begin{multline}\nonumber \shoveleft \text{Complete parallelograms } EBPD, ECQA \text{ such that }\\ \shoveleft EB \parallel DP, ED \parallel BP, EC \parallel AQ, EA \parallel CQ\\ \shoveleft \text{Let } AQ, BP \text{ intersect with } DF \text{ at } L, K \implies \\ \shoveleft \dfrac{FC}{CL}=\dfrac{FB}{BA}=\dfrac{FK}{KD} \implies \dfrac{FC}{FK}=\dfrac{CL}{KD}=\dfrac{CQ}{KP}\\ \shoveleft \implies \triangle{FCQ} \sim \triangle{PFKP} \implies F,Q,P \text{ are collinear}\\ \shoveleft \text{Diagonal }EP \text{ of parallelogram }EBPD \text{ is bisected at }M\\ \shoveleft \text{Diagonal }EQ \text{ of parallelogram }ECQA \text{ is bisected at }H\\ \shoveleft \implies MH \parallel PQ, \text{Similarly, } HG \parallel QF\\ \shoveleft F,Q,P \text{ are collinear} \implies G,H,M \text{ are collinear}\blacksquare \end{multline}\)

Prove 4: \(\begin{multline}\nonumber \shoveleft \text{Lemma 1: The locus of points } X \text{ in the interior of } ABCD \\ \shoveleft \text{ such that } [XAB]+[XCD]= \dfrac{[ABCD]}{2} \text{ is a line segment. }\\ \shoveleft \text{In triangle } ADE \text{, consider a translation of } AB \text{ to } ES \text{ and } CD \text{ to } ET\\ \shoveleft \implies [XES]=[XAB] , [XET]=[XCD]\\ \shoveleft \implies [XAB]+[XCD]=[XES]+[XET]=[XSET]=[EST]+[XST]\\ \shoveleft S, T \text{ are fixed points } \implies [XST] \text{ is constant} \implies \text{the locus of } X \\ \shoveleft \text{ is the segment made by the intersection of the line parallel to } ST \text{ with } ABCD. \\ \shoveleft \text{Further note that } X \text{ is outside } ABCD \implies \bigg|[XAB]−[XCD]\bigg|=\dfrac{[ABCD]}{2} \blacksquare\\ \shoveleft \text{Note that } N \text{ is the midpoint of } AC \implies [ANB]=[BNC], [AND]=[CND]\\ \shoveleft \implies [ANB]+[CND]=\dfrac{[ABCD]}{2} \implies N \text{ lies on the locus of } X.\\ \shoveleft \text{Similarly, } M \text{ lies on the locus of } X.\\ \shoveleft \text{Now note that } EP=PF, [PAB]=\dfrac{[FAB]}{2}, [PCD]=\dfrac{[FCD]}{2} \implies\\ \shoveleft [PAB]−[PCD]=\dfrac{([FAB]−[FCD])}{2}=\dfrac{[ABCD]}{2}\\ \shoveleft \implies P \text{ also lies on this line } \implies M, N, P \text{ are collinear.} \blacksquare \end{multline}\) Reference:

09/28/2023

The distances of a point $D$ to the vertices of an equilateral triangle $\triangle{ABC}$ are $3,5,7$. Find the area of this triangle.

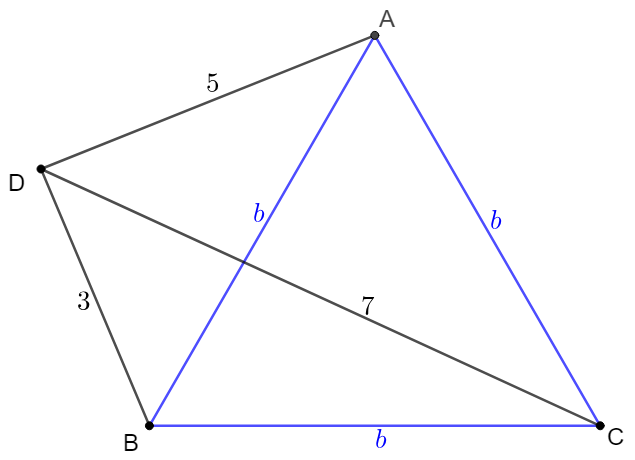
image-20230928201915007

Solve:

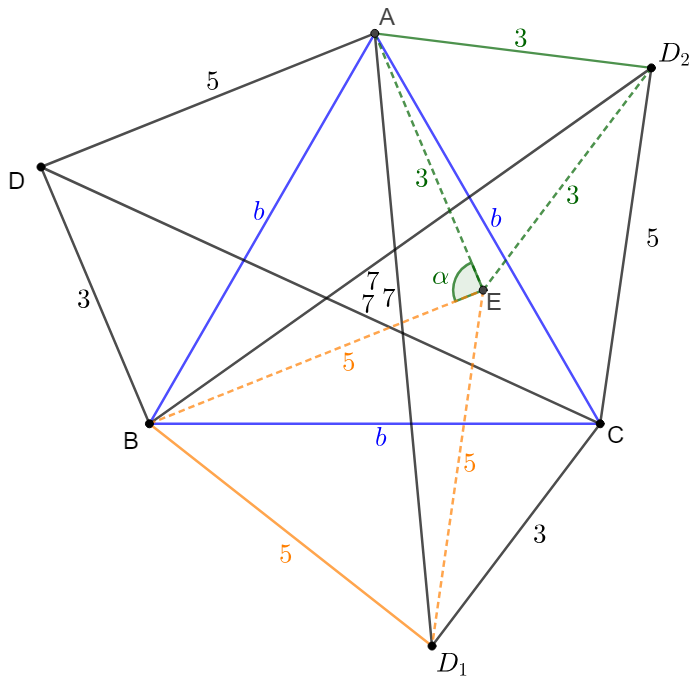image-20230928201757337 \(\begin{multline}\nonumber \shoveleft \text{Make point } D_1, D_2 \text{ such that } \triangle{ABD}\cong\triangle{BCD_1}\cong\triangle{CAD_2}\\ \shoveleft \text{Make point } E \text{ such that } AE \parallel DB, D_2E \parallel CD_1, \text{ connect }AE,BE,D_1E,D_2E\\ \shoveleft AE=D_1E=AD_2=3, BE=BD_1=D_1E=5, CD=B_2=AD_1=7\\ \shoveleft \implies \triangle{AD_2E}, \triangle{BED_1} \text{ are equilateral}, ADBE, CD_1ED_2 \text{ are parallelograms}\\ \shoveleft cos(\angle{AED_1})=\dfrac{3^3+5^2-7^2}{2 \cdot 3\cdot 5}=-\dfrac{1}{2}\implies \angle{AED_1}=120^{\circ}\implies \angle{AEB}=60^{\circ}\\ \shoveleft \implies cos(60^{\circ})=\dfrac{3^2+5^2-AB^2}{2 \cdot 3 \cdot 5} \implies AB=\sqrt{19}\implies [ABC]=\bbox[5px, , border: 1px solid black]{\dfrac{19\sqrt{3}}{4}} \end{multline}\)

09/30/2023

Point $A$ is outside circle and point $F$ is on the circle such that $AB, AC$ is the tangent lines with $B,C$ are the tangent points. Extend $AB, AC$ to $D, E$ such that $FD\perp AD, FE \perp AE, FD=9, FE=4, FG \perp BC$, find $FG$.

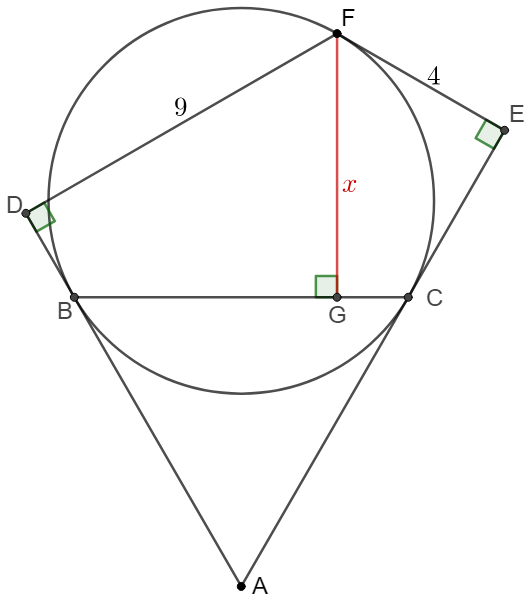
image-20230930004100407

Solve:

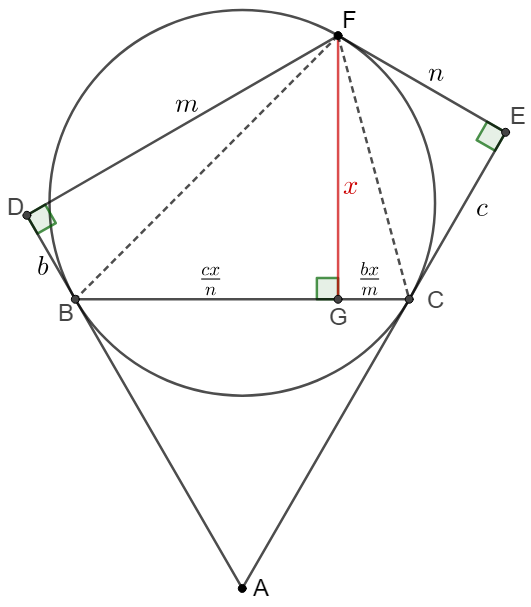image-20230930003937060 \(\begin{multline}\nonumber \shoveleft \text{Let }DF=m, EF=n, BD=b, CE=c, FG=x\\ \shoveleft FD\perp AD, FG \perp BC,EF \perp AE \implies DBGF, CEFG \text{ are cyclic}\\ \shoveleft \implies \angle{ABC}=\angle{ACB}=\angle{BFC}=\angle{DFG}=\angle{EFG} \\ \shoveleft \implies \angle{BFD}=\angle{CFG}, \angle{BFG}=\angle{CFE}\\ \shoveleft \implies \dfrac{m}{b}=\dfrac{x}{CG}, \dfrac{n}{c}=\dfrac{x}{BG} \implies BG=\dfrac{cx}{n}, CD=\dfrac{bx}{m} \\ \shoveleft \implies m^2+b^2=\dfrac{n^2+c^2}{n^2}x^2, n^2+c^2=\dfrac{m^2+b^2}{m^2}x^2\\ \shoveleft \implies n^2+c^2=\dfrac{\dfrac{n^2+c^2}{n^2}x^2}{m^2}x^2 \implies x=\sqrt{mn}=\bbox[5px, border: 1px solid black]{6} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search