08/02/2023
Find the values of $a$ such that $x^2 + ax + 5a = 0$ has only integer solutions.
Solve: \(\begin{multline}\nonumber \shoveleft \text{Suppose the equation has roots } m \text{ and } n \implies (x-m)(x-n)=0\\ \shoveleft \implies x^2-(m+n)x+mn=0 \implies m+n=-a, mn=5a\\ \shoveleft \implies mn+5(m+n)=0 \implies (m+5)(n+5)=25\\ \shoveleft \implies m+5=25, n+5=1 \implies \bbox[5px, border: 1px solid black]{m=20, n=-4}\\ \shoveleft \text{ or } m+5=-25, n+5=-1 \implies \bbox[5px, border: 1px solid black]{m=-30, n=-6}\\ \shoveleft \text{ or } m+5=1, n+5=25 \implies \bbox[5px, border: 1px solid black]{m=-4, n=20}\\ \shoveleft \text{ or } m+5=-1, n+5=-25 \implies \bbox[5px, border: 1px solid black]{m=-6, n=-30}\\ \shoveleft \text{ or } m+5=5, n+5=5 \implies \bbox[5px, border: 1px solid black]{m=n=0}\\ \shoveleft \text{ or } m+5=-5, n+5=-5 \implies \bbox[5px, border: 1px solid black]{m=n=-10} \end{multline}\)
08/03/2023
Positive integers $x, y, z$ satisfying $x \le y \le z, xyz=2(x+y+z)$, find the sum of possible $z$.
Solve: \(\begin{multline}\nonumber \shoveleft \text{Check the possible values of }x, \text{ easy to see that } x<3.\\ \shoveleft \text{If } x \ge 3, \text{ then } z \ge y \ge x \ge 3 \implies xyz \ge 3yz = yz + yz + yz \ge 3x + 3y + 3z\\ \shoveleft \text{ this is inconsistent with } xyz=2(x+y+z), \text { so we must have } 3 \gt x \ge 1 \\ \shoveleft \text{ If } x=2, \text{ then } xyz=2yz=2(2+y+z) \implies yz=y+z+2 \implies y=2, z=4\\ \shoveleft \text{ If } x=1, \text{ then } xyz=yz=2(1+y+z) \implies y=3, z=8 \text{ or }y=4, z=5\\ \shoveleft \text{ so the sum of possible }z \text{ is } 4+5+8 = \bbox[5px, border: 1px solid black]{17} \end{multline}\)
08/04/2023
In quadrilateral $ABCD$, $AC \perp BD, \angle{ABD}=20^{\circ}, \angle{ADB}=50%{\circ}, \angle{BDC}=30^{\circ}$, find $\angle{CBD}$.
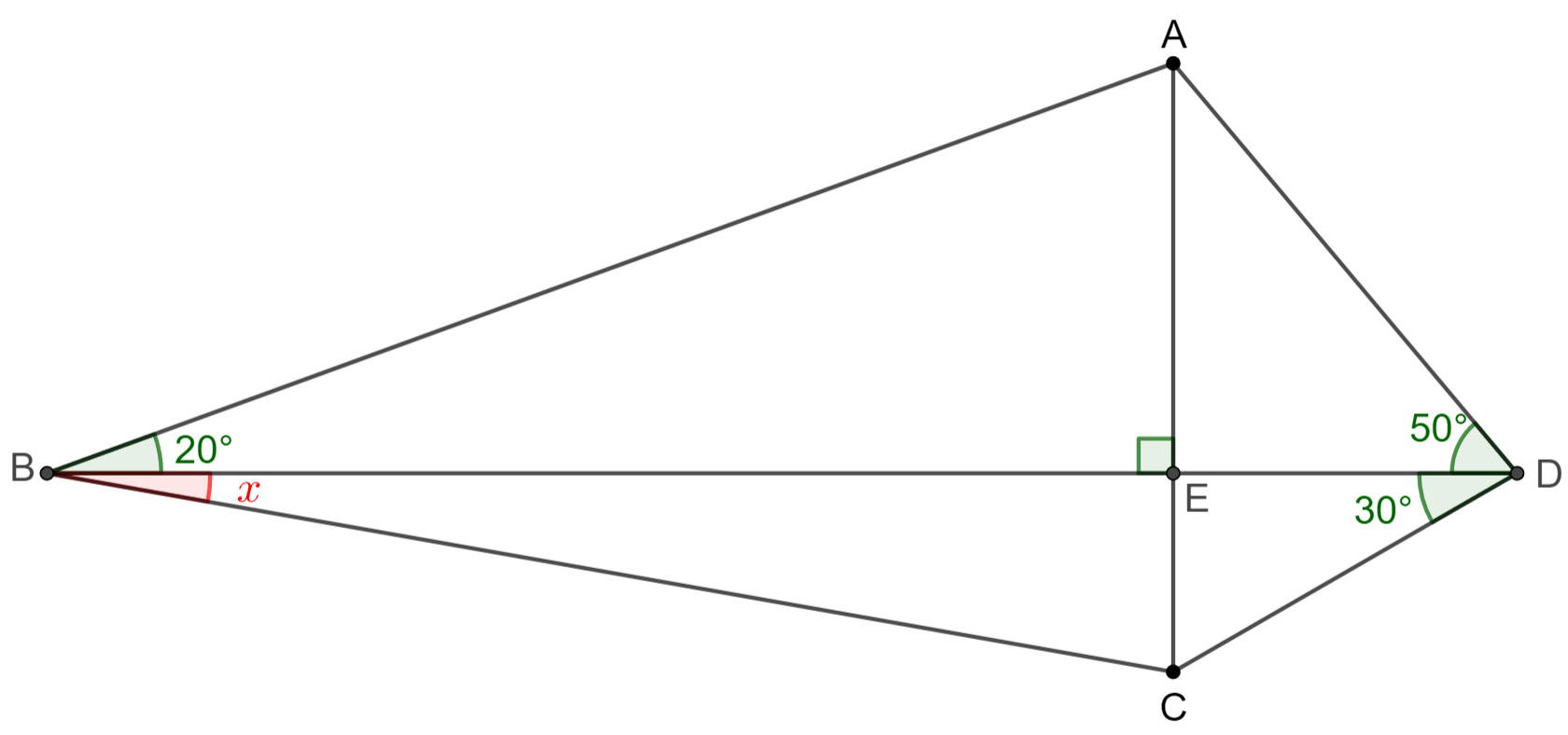
Solve:
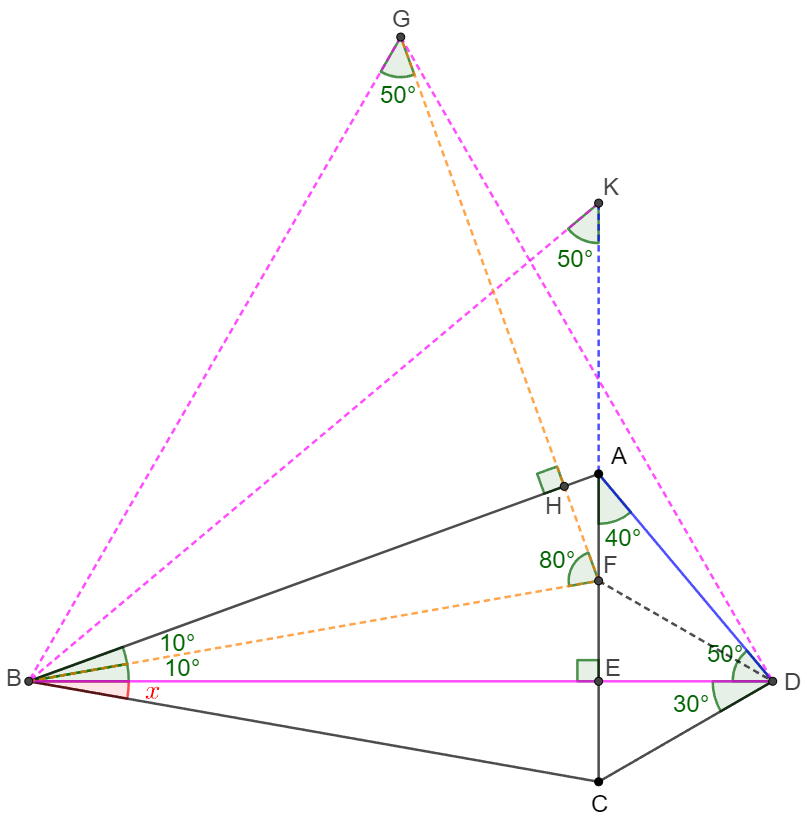\(\begin{multline}\nonumber
\shoveleft \text{Make point } F \text{ on } AE \text{ such that } \angle{EBF}=10^{\circ}, \text{ connect DF}\\
\shoveleft \text{Extend } EA \text{ to } K \text{ such that } AK=AD \implies \angle{BAK}=180^{\circ}-\angle{BAE}=110^{\circ}=\angle{BAD}\\
\shoveleft \implies \triangle{BAK}\cong \triangle{BAD} \implies BD=BK, \angle{BKA}=\angle{BDA}=50^{\circ}\\
\shoveleft \text{Make } H \text{ on } AB \text{ such that } FH\perp AB \implies \triangle{FBE} \cong \triangle{FBH} \implies BE=BH\\
\shoveleft \text{Extend } FH \text{ to } G \text{ such that } BF=BG \implies \angle{BFG}=80^{\circ}, \angle{BGF}=\angle{FBG}=50^{\circ} = \angle{BKE}\\
\shoveleft \implies \triangle{BGH} \cong \triangle{BKE} \implies BG=BK=BD, \text{ since } \angle{BDG}=60^{\circ}\implies \triangle{BDG} \text{ is equilateral}\\
\shoveleft \implies BD=DG \implies \triangle{BDF}\cong \triangle{GDF} \implies \angle{BDF}=\dfrac{\angle{BDG}}{2}=30^{\circ}\implies \triangle{CDE}\cong\triangle{FDE}\\
\shoveleft \implies CD=FD \implies \triangle{BCD} \cong \triangle{BFD} \implies \angle{CBD}=\angle{FBD}=\bbox[5px, border: 1px solid black]{10^{\circ}}\\
\end{multline}\)
Note: this problem is related to a previous problem
08/05/2023
$\triangle{ABC}$ has $\angle{ABC}=20^{\circ}, \angle{ACB}=40^{\circ}$, $D$ is a point inside the triangle such that $\angle{DBC}=\angle{DCB}=10^{\circ}$, find $\angle{BAD}$.
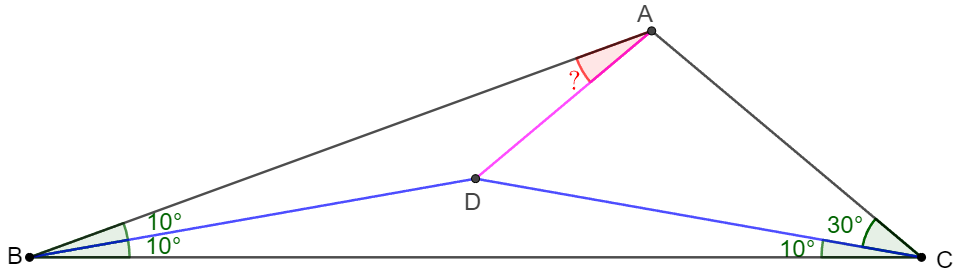
Solve:
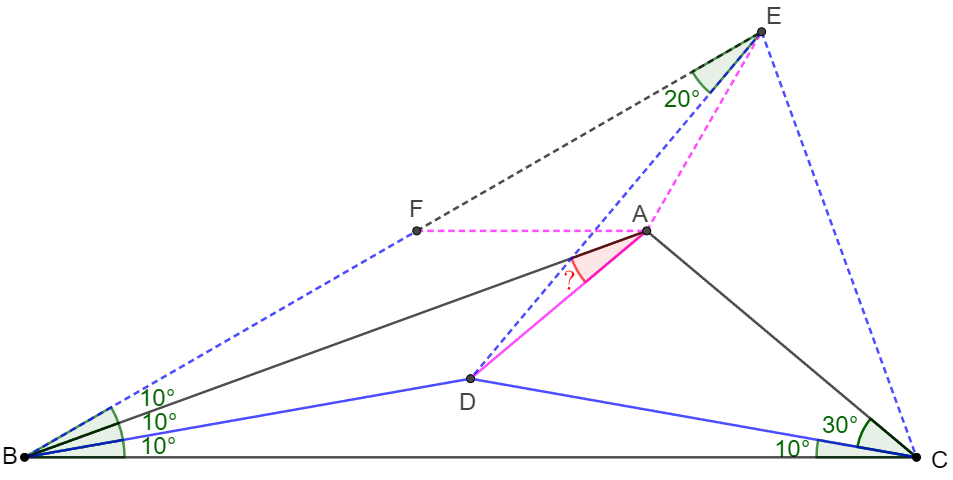\(\begin{multline}\nonumber
\shoveleft \text{Make equilateral triangle } \triangle{CDE} \text{ such that } E \text{ is on the same side of } CD \text { as point } A.\\
\shoveleft \text{Connect } AE, BE, CE, DE.\text{Let } F \text{ on } BE \text{ such that } BD=BF, \text{ connect } AF.\\
\shoveleft \angle{ACD}=30^{\circ}=\angle{ACE}, CD=CE \implies \triangle{ACD} \cong \triangle{ACE} \implies AD=AE\\
\shoveleft \angle{BCD}=\angle{CBD} \implies BD=CD=DE \implies \angle{EBD}=\angle{BED}=\dfrac{180^{\circ}-2(60^{\circ}+10^{\circ})}{2}=20^{\circ}\\
\shoveleft \implies \angle{ABF}=10^{\circ}=\angle{ABD}, BD=BF \implies \triangle{ABD} \cong \triangle{ABF} \implies \angle{ADB}=\angle{AFB}, AF=AD=AE\\
\shoveleft \implies \angle{AEF}=\angle{AFE} \implies \angle{ADB}+\angle{AEF}=\angle{AFB}+\angle{AFE}=180^{\circ} \implies ADBE \text{ is cyclic}\\
\shoveleft \implies \angle{BAD}=\angle{BED}=\bbox[5px, border: 1px solid black]{20^{\circ}}\\
\end{multline}\)
08/06/2023
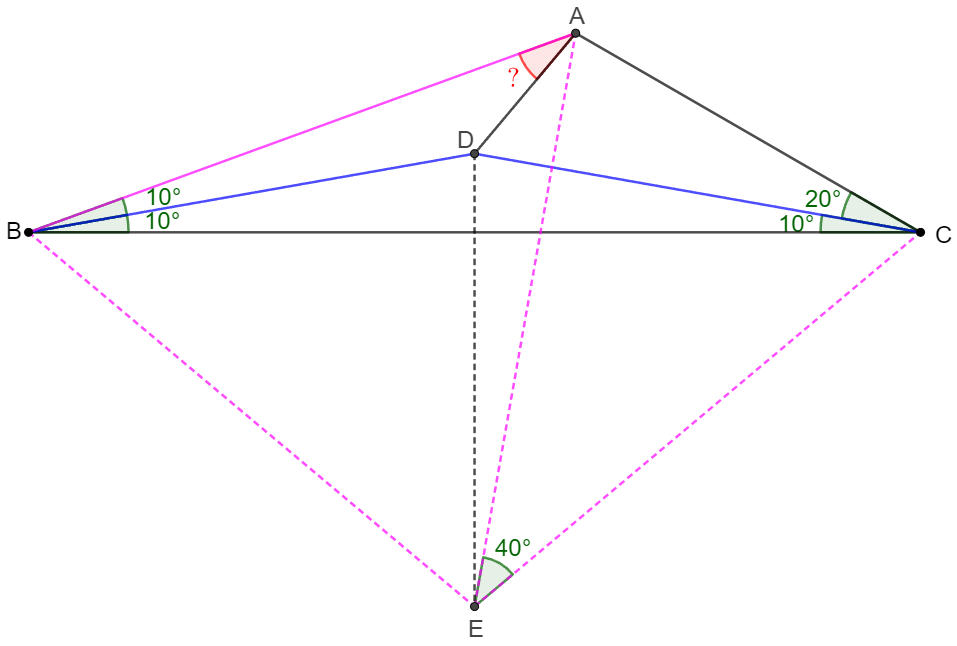
$\triangle{ABC}$ has $\angle{ABC}=20^{\circ}, \angle{ACB}=30^{\circ}$, $D$ is a point inside the triangle such that $\angle{DBC}=\angle{DCB}=10^{\circ}$, find $\angle{BAD}$.
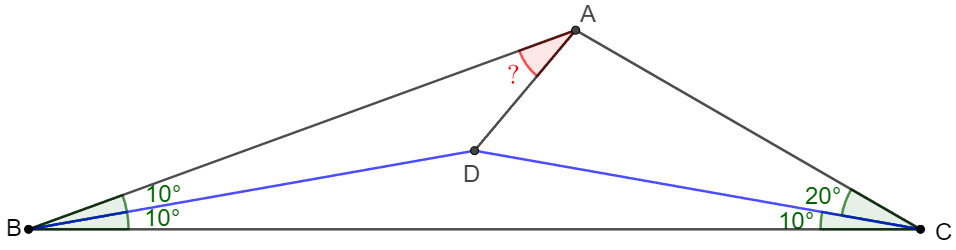
Solve:
\(\begin{multline}\nonumber
\shoveleft \text{Make equilateral triangle } \triangle{ABE} \text{ such that } E \text{ is on the same side of } AB \text{ as point }D.\\
\shoveleft AE=BE, \angle{ABE}=2\angle{ACB} \implies E \text{ is circumcenter of }\triangle{ABC}\\
\shoveleft \implies \angle{AEC}=2\angle{ABC}=40^{\circ}, BE=AE=CE \implies \angle{EAC}=\angle{ECA}=70^{\circ}\\
\shoveleft \implies \angle{EBC}=\angle{ECB}=70^{\circ}-30^{\circ}=40^{\circ}\\
\shoveleft BD=CD, BE=CE \implies \triangle{BED}\cong\triangle{CED} \implies \angle{CED}=\angle{BED}= \dfrac{180^{\circ}-2*40^{\circ}}{2}=50^{\circ}=\angle{EBD}\\
\shoveleft \implies BD=ED, \angle{AED}=10^{\circ}=\angle{ABD} \implies \triangle{ABD} \cong \triangle{AED} \implies \angle{BAD}=\dfrac{60^{\circ}}{2}=\bbox[5px, border: 1px solid black]{30^{\circ}} \\
\end{multline}\)
08/06/023
$a+\dfrac{1}{b}=3, b+\dfrac{1}{c}=17, c+\dfrac{1}{a}=\dfrac{11}{25}$, find $abc$.
Solve: \(\begin{multline} \nonumber \shoveleft (a+\dfrac{1}{b})(b+\dfrac{1}{c})=ab+1+\dfrac{a}{c}+\dfrac{1}{bc}=51 \implies ab+\dfrac{a}{c}+\dfrac{1}{bc}=50\\ \shoveleft \implies (ab+\dfrac{a}{c}+\dfrac{1}{bc})(c+\dfrac{1}{a})=abc+b+a+\dfrac{1}{c}+\dfrac{1}{b}+\dfrac{1}{abc}=22\\ \shoveleft \implies abc+\dfrac{1}{abc}=22-17-3=2\implies (abc-1)^2=0\implies abc=\bbox[5px, border: 1px solid black]{1} \end{multline}\)
08/09/2023
Prove that every odd integer that does not have 5 as its ones digit is a factor of some integer consisting of only 9 as its digits.
Prove: . \(\begin{multline}\nonumber \shoveleft \text{For any odd integer } N \text{ that does not have }5 \text{ has its ones digit, it does not have factor of } 2 \text{ and } 5, \text{ so } 10 \text{ is not factor of } N.\\ \shoveleft \text{Now we prove the claim by construction: consider the } (N+1) \text{ numbers that contains }1, 2, \dots, (N+1) \text{ digits of } 9s.\\ \shoveleft 9, 99, 999, \dots, 99\dots9, \text{ where the last number has } (N+1) \text{ digits of } 9s.\\ \shoveleft \text{Since there are } (N+1) \text{numbers in this list, there are at least two numbers having the same modular values on } N. \\ \shoveleft \text{ Let } d \text{ be the difference of these two numbers, it will be in format of } 99\dots9 * 10^k. \text{ Let } d = 99\dots9 * 10^k = m*N. \\ \shoveleft \text{And we know that } 10 \text{ is not factor of } N, \text{that means } 10^k \text{ are factor of } m. \text{ Thus we have } 99\dots9 = p*N.\\ \shoveleft \text{This means } N \text{ is a factor of } 99\dots9. \blacksquare \end{multline}\)
08/22/2023
$\triangle{ABC}$ has $\angle{ACB}=30^{\circ}, \angle{BAC}=110^{\circ}$, $D$ is a point inside the triangle such that $\angle{DAC}=40^{\circ}, \angle{DCA}=20^{\circ}$, find $\angle{DBC}$.
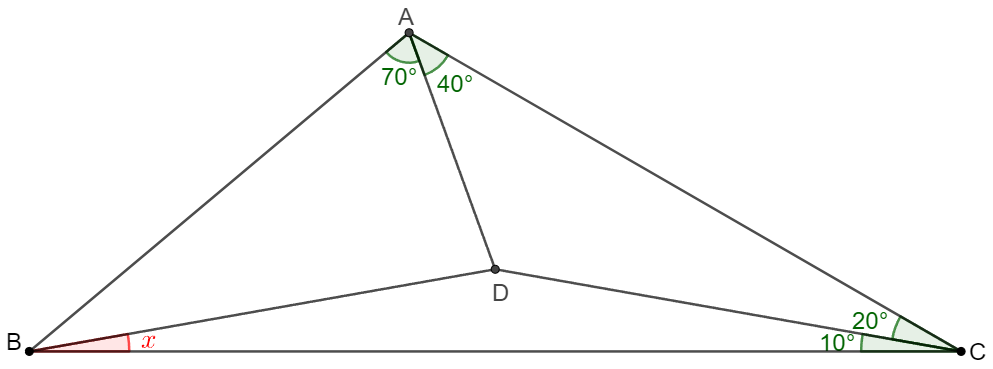
Solve:
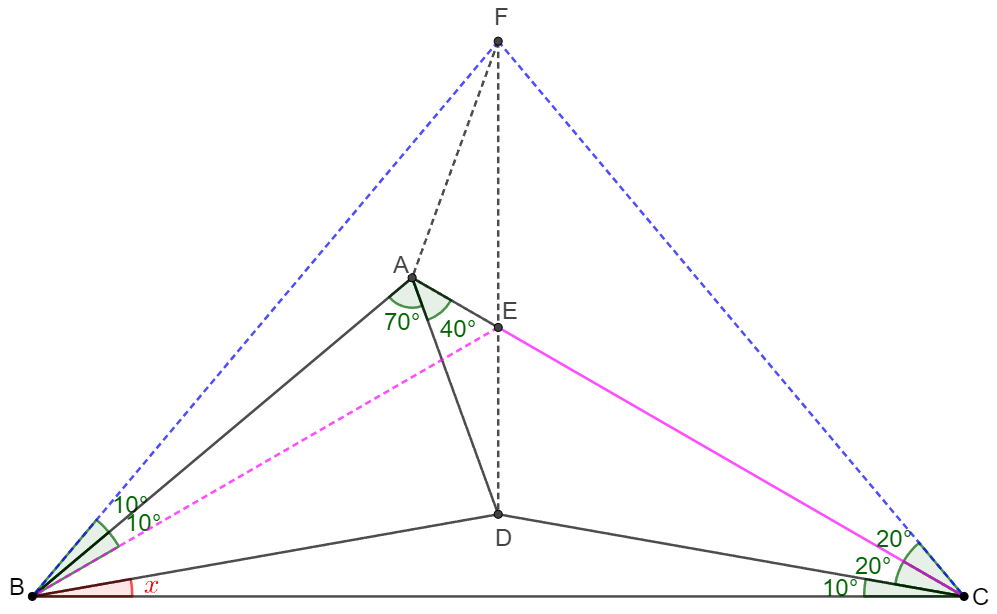\(\begin{multline}\nonumber
\shoveleft \text{Let } E \text{ be the intersection of } AC \text{ and perpendicular bisector of } BC.\\
\shoveleft \text{ Let } F \text{ be a point on perpendicular bisector of } BC \text{ such that } \angle{FBC}=50^{\circ}, \text{Connect } DE.\\
\shoveleft \implies BE=CE, \angle{EBC}=\angle{ECB}=30^{\circ}, BF=CF, \angle{FBA}=\angle{EBA}=10^{\circ}, \angle{FCE}=\angle{DCE}=20^{\circ}\\
\shoveleft \implies \angle{BEC}=120^{\circ}=\angle{AEB}=\angle{AEC}\implies AE \text{ bisects } \angle{AEB} \implies A \text{ is incenter of }\triangle{ABE}\\
\shoveleft \implies \angle{BFA}=\angle{AFE}=20^{\circ} \implies \angle{AFC}=20^{\circ}+40^{\circ}=60^{\circ}=180^{\circ}-\angle{ADC} \implies ADCF \text{ is cyclic}\\
\shoveleft \implies \angle{AFD}=\angle{ACD}=20^{\circ}=\angle{AFE} \implies DEF \text{ is colinear} \implies \triangle{BDE}\cong \triangle{CDE} \implies \angle{DBC}=\angle{BCD}=\bbox[5px, border: 1px solid black]{10^{\circ}}
\end{multline}\)