07/26/2023
There are $a_1, a_2, \dots, a_m \in { 1, 2, \dots, m }$, $b_1, b_2, \dots, b_m \in { 1, 2, \dots, m }$. Prove that there exists $1 \le p \le q \le m$ and $1 \le s \le t \le m$ such that $a_p + \dots + a_q = b_s + \dots + b_t$ (from 2023 Beijing NCEE)
Prove: \(\begin{multline}\nonumber \shoveleft \text{Let } A_i = a_1 + a_2 + \dots + a_i, B_i = b_1 + b_2 + \dots + b_m, (1 \le i \le m), A_0=B_0=0.\\ \shoveleft \text{And Let } r_k=max\{ i | B_i \le A_k, k \in \{0, 1, \dots, m\}\}\\ \shoveleft \text{Without Loss of Generality, we assume } A_m \ge B_m. \text{ Let } S_k = A_k - B_{r_k} \text{ for }1 \le k \le m \implies S_k \ge 0.\\ \shoveleft \text{From the definition of } r_k \implies A_k-B_{r_k+1} < 0 \implies b_{r_k+1}=B_{r_k+1}-B_{r_k}= S_k - (A_k-B_{r_k+1})\\ \shoveleft b_{r_k+1} \in \{1,2, \dots, m\} \implies b_{r_k+1} \le m \implies S_k \le m + (A_k - B_{r_k+1}) \lt m \implies S_k \le m-1\\ \shoveleft \text{If } \exists k \text{ such that } S_k=0 \implies r=p=1, q=k,s=r_k, a_1+\dots+a_q=A_k=B_{r_k}=b_1+\cdots+b_{r_k}\blacksquare\\ \shoveleft \text{If } \nexists k \text{ such that }S_k=0 \implies S_k \in \{ 1,2,\dots, m-1 \} \text{ for } k \in \{ 1,2, \dots, m\} \\ \shoveleft \implies \exists 1 \le u \lt v \le m \text{ such that } S_u=S_v \implies A_u-B_{r_u}=A_v-B_{r_v} \implies A_v-A_u=B_{r_v}-B_{r_u}\\ \shoveleft \implies p=v-u+1, q=v, s=r_v-r_u+1, t=r_v, a_{v-u+1}+\dots+a_v=b_{r_v-r_u+1}+\dots+b_{r_v}\blacksquare\\ \shoveleft \text{Similarly the conclusion holds when } B_m \ge A_m. \text{ Done. }\blacksquare \\ \end{multline}\\\)
07/27/2023
In quadrilateral $ABCD$, $AC$ and $BD$ intersects at $O$. $\angle{CBD}=20^{\circ}, \angle{BDC}=25^{\circ}, \angle{BAC}=50^{\circ}, \angle{CAD}=40^{\circ}, find \angle{AOB}.$
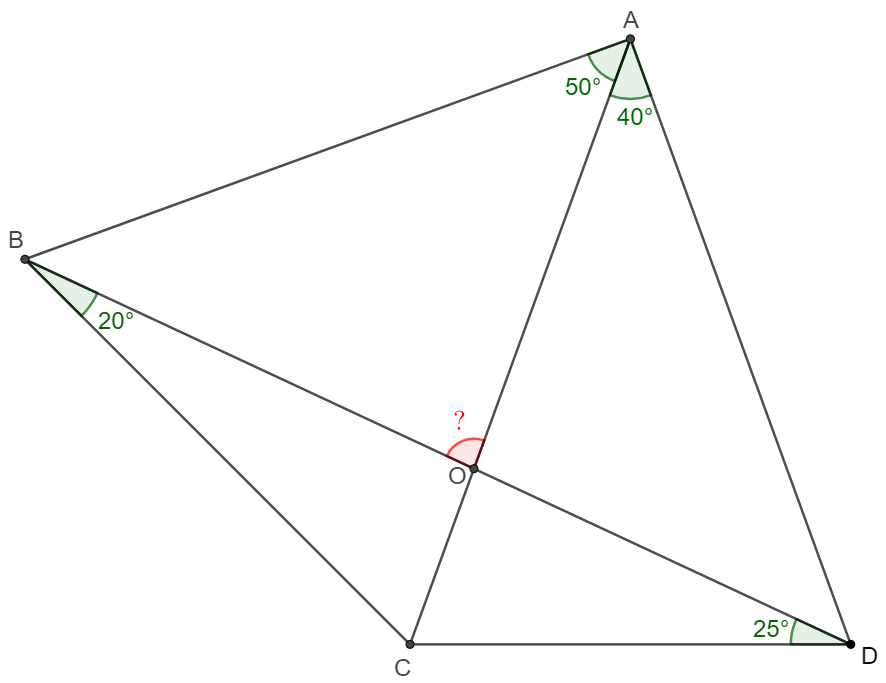
Solve:
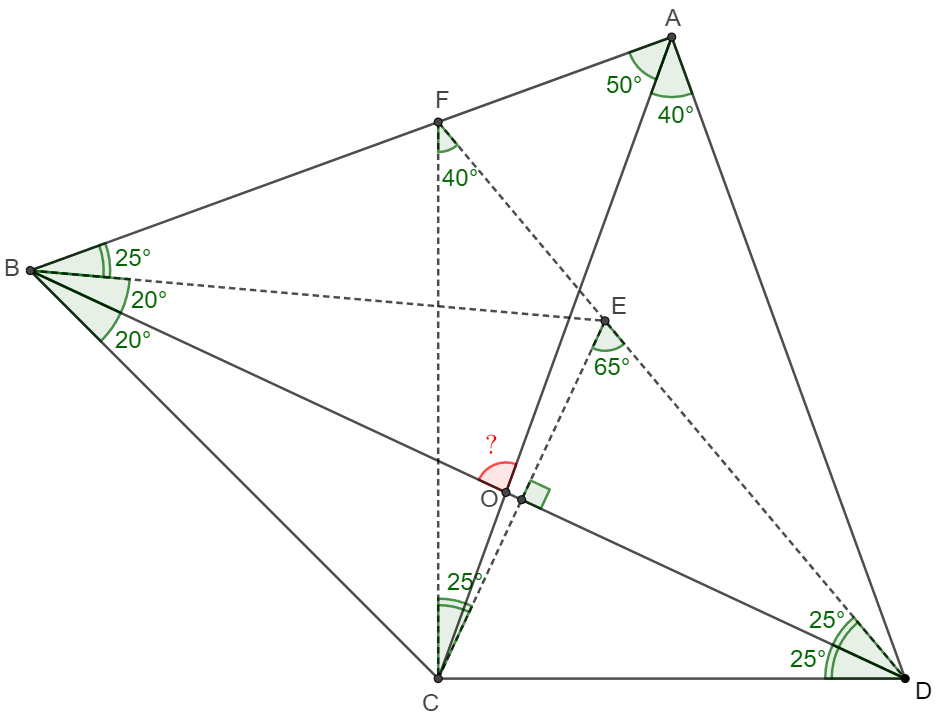
. \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ be the mirror point of } C \text{ over line }BD, \text{ Connect } BE, CE \implies CE \perp BD \\ \shoveleft \angle{EBD}=\angle{CBD}=20^{\circ}, \angle{CBE}=40^{\circ}, \angle{EDB}=\angle{CDB}=25^{\circ}, \angle{CED}=90^{\circ}-25^{\circ}=65^{\circ}\\ \shoveleft \text{ Extend } DE \text{ and intersect with } AB \text{ at } F. \angle{CDF}=50^{\circ}=\angle{CAF} \implies AFCD \text{ is cyclic. }\\ \shoveleft \implies \angle{CFD}=\angle{CAD}=40^{\circ}=\angle{CBE} \implies \angle{ECF}=65^{\circ}-40^{\circ}=25^{\circ}, BCEF \text{ is cyclic}\\ \shoveleft \implies \angle{EBF}=\angle{ECF}=25^{\circ} \implies \angle{AOB}=180^{\circ}-50^{\circ}-45^{\circ}=\bbox[5px, border: 1px solid black]{85^{\circ}}\\ \end{multline}\)