06/02/2023
Circle $O$ is inside rectangle $ABCD$. The tangent lines from $A,B,C,D$ to $\odot{O}$ have lengths as $AE=31, BF=34, DH=46$, find $CG$.
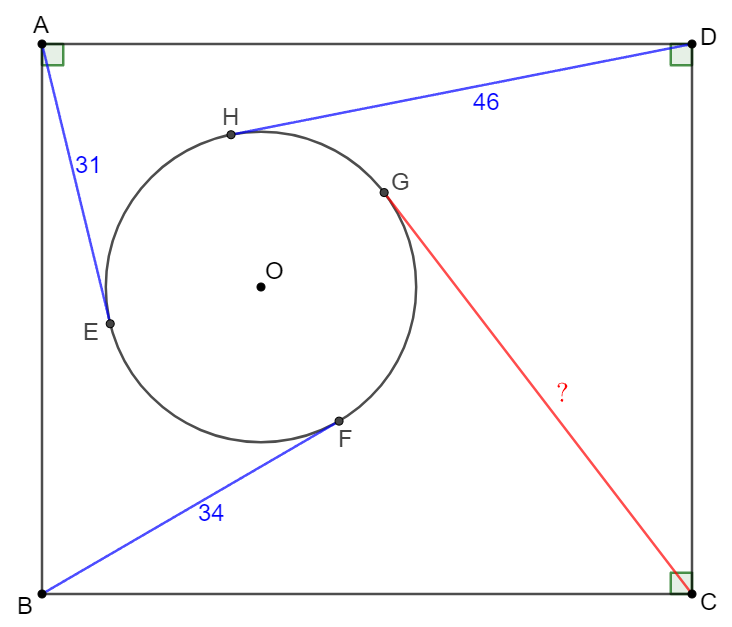
solve:
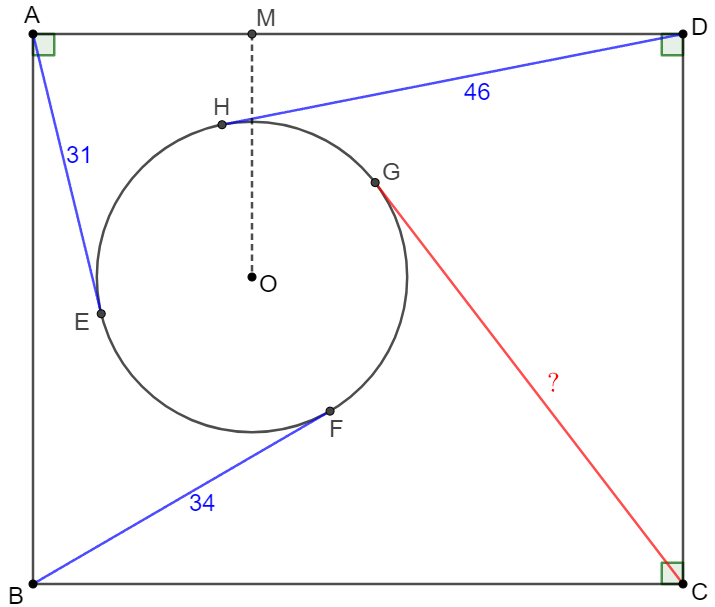
. \(\begin{multline}\nonumber \shoveleft \text{Suppose the radius of } \odot{O} \text{ is } r, then\\ \shoveleft AO^2=AE^2+r^2, CO^2=CG^2+r^2\\ \shoveleft BO^2=BF^2+r^2, DO^2=DH^2+r^2\\ \shoveleft \text{And it's easy to see that } \\ \shoveleft AO^2+CO^2=AM^2+MO^2+(AD-AM)^2+(AB-MO)^2\\ \shoveleft BO^2+DO^2=AM^2+(AB-MO)^2+MO^2+(AD-AM)^2\\ \shoveleft \implies AO^2+CO^2=BO^2+DO^2\\ \shoveleft CG^2=CG^2+BF^2-AE^2=34^2+46^2-31^2=2311\\ \shoveleft \implies CG=\bbox[5px, border: 1px solid black]{\sqrt{2311}} \end{multline}\)
06/03/2023
Quadrilateral $ABCD$ has area of $72$. $BD=12, CE=3AE, AD=CD, \angle{ADC}=90^{\circ}$, find the area of $\triangle{ABC}=[ABC]$.
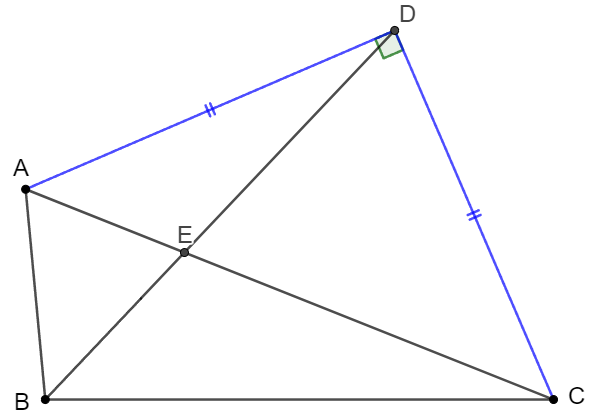
Solve 1:
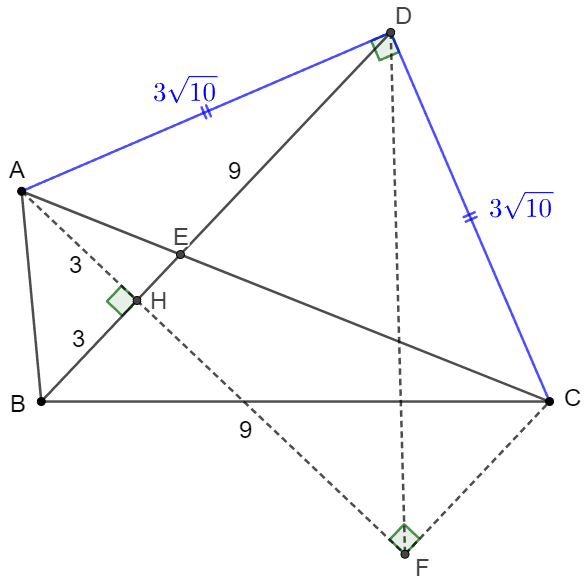
. \(\begin{multline}\nonumber \shoveleft \text{Make } AF \perp BD\\ \shoveleft CF \parallel BD, AF \text{ intersects with } BD \text{ at }H, \text{ intersects with } CF \text{ at } F.\\ \shoveleft [ABCD]=\dfrac{AF \cdot BD}{2}=72 \implies AF=12, CE=3AE, \triangle{AHE}\sim\triangle{AFC}\\ \shoveleft \implies AH=3, HF=9, \angle{AFC}=\angle{ADC}=90^{\circ} \implies AFCD \text{ is cyclic }\\ \shoveleft \implies \angle{AFD}=\angle{ACD}=45^{\circ} \implies DH=FH=9\\ \shoveleft \implies AD=\sqrt{AH^2+DH^2}=3\sqrt{10} \implies [ACD]=\dfrac{AD^2}{2}=45\\ \shoveleft \implies [ABC]=[ABCD]-[ACD]=72-45=\bbox[5px, border: 1px solid black]{27} \end{multline}\)
Solve 2:
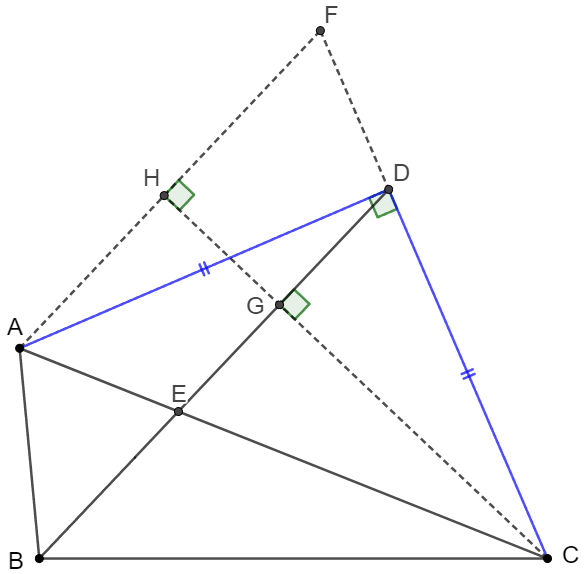
. \(\begin{multline}\nonumber \shoveleft \text{Make } AF \parallel BD, F \text{ on extended } CD.\\ \shoveleft \text{ Make } CH \perp AF \text{ and intersects with } AF \text{ at } H, \text{ intersects with } BD \text{ at } G\\ \shoveleft [ABCD]=\dfrac{AF \cdot CH}{2}=72 \implies CH=12, CE=3AE\\ \shoveleft \implies CD=AD=3DF \implies AF=\sqrt{10} DF\\ \shoveleft [ACF]=\dfrac{AD\cdot CF}{2}=\dfrac{3DF \cdot 4DF}{2}=6DF^2=\dfrac{AF\cdot CH}{2}=\dfrac{12 \cdot \sqrt{10}DF}{2}\\ \shoveleft \implies DF=\sqrt{10}\implies CD=3\sqrt{10}\implies [ACD]=\dfrac{CD^2}{2}=45\\ \shoveleft \implies [ABC]-[ABCD]-[ACD]=72-45= \bbox[5px, border: 1px solid black]{27} \end{multline}\)
06/08/2023
$m, n$ are real numbers. $m^3 + n^3 + 3mn - 1 = 0$. Find $m+n$.
Solve:
. \(\begin{multline}\nonumber \shoveleft m^3 + n^3 + 3mn - 1\\ \shoveleft = (m+n)^3 - 3mn(m+n) + 3mn -1\\ \shoveleft =[(m+n)^3 - 1] - [3mn(m+n)-3mn]\\ \shoveleft =(m+n-1)[(m+n)^2 + (m+n) +1] -3mn(m+n-1)\\ \shoveleft =(m+n-1)[(m+n)^2 +m+n-3mn+1]\\ \shoveleft = (m+n-1)(m^2-mn+n^2+m+n+1)\\ \shoveleft = (m+n-1)(2m^2-2mn+2n^2+2m+2n+2)\\ \shoveleft = (m+n-1)[(m-n)^2+(m+1)^2+(n+1)^2]=0\\ \shoveleft \implies m+n-1=0 \text{ or } (m-n)^2+(m+1)^2+(n+1)^2=0\\ \shoveleft \implies m+n= \bbox[5px, border: 1px solid black]{1} \text{ or } m=n=-1\implies m+n= \bbox[5px, border: 1px solid black]{-2} \end{multline}\)
06/25/2023
$\triangle{ABC}$ is isosceles with $\angle{B}=\angle{C}=\alpha$, $D$ is the midpoint of $BC$ and $E$ is a point on $BC$, $F$ is the midpoint of $CE$, $G$ is the point inside the triangle such that $\angle{GFD}=2\angle{B}=2\alpha, DF=GF$ . Prove: $AG\perp EG$
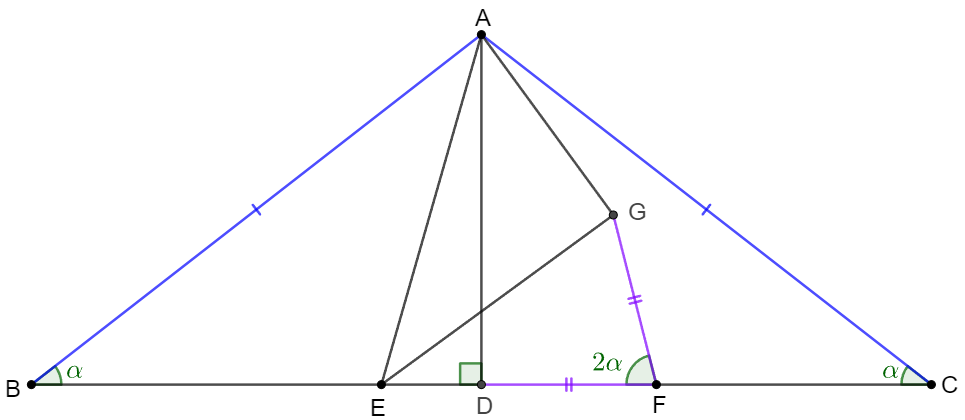
Prove 1:
.
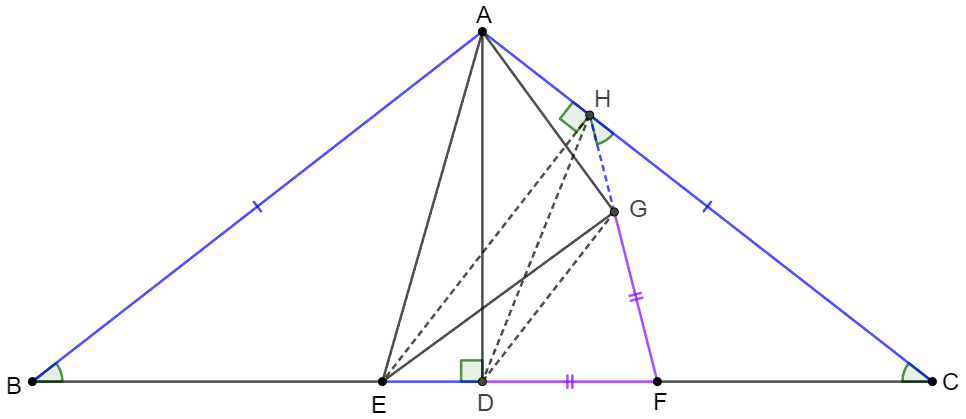\(\begin{multline}\nonumber
\shoveleft \text{Extend }FG \text{ and intersect with } AC \text{ at } H. \text{ Connect } DG, EH, DH \\
\shoveleft \angle{GFD}=2\angle{B}=2\angle{C} \implies \angle{FHC}=\angle{C} \implies CF=FH=EF\\
\shoveleft \implies \angle{FEH}=\angle{EHF} \implies \angle{EHF}+\angle{FHC}=90^{\circ} \implies EH \perp AC\\
\shoveleft \text{Easy to see } AD\perp BC \implies AEDH \text{ is cyclic } \implies \angle{EAC}=\angle{HDF}\\
\shoveleft DF=GF, EF=HF \implies DE=GH, \angle{FDG}=\angle{DGF}\\
\shoveleft \implies \angle{DGH}=\angle{GDE} \implies \triangle{EDG} \cong \triangle{HGD} \implies \angle{DGE}=\angle{GDH}\\
\shoveleft \implies \angle{HDF}=\angle{EGF} \implies \angle{EAC}=\angle{EGF}\implies AEGH \text{ is cyclic}\\
\shoveleft \implies \angle{AGE}=\angle{AHE}=90^{\circ} \implies AG \perp EG \blacksquare
\end{multline}\)
Prove 2:
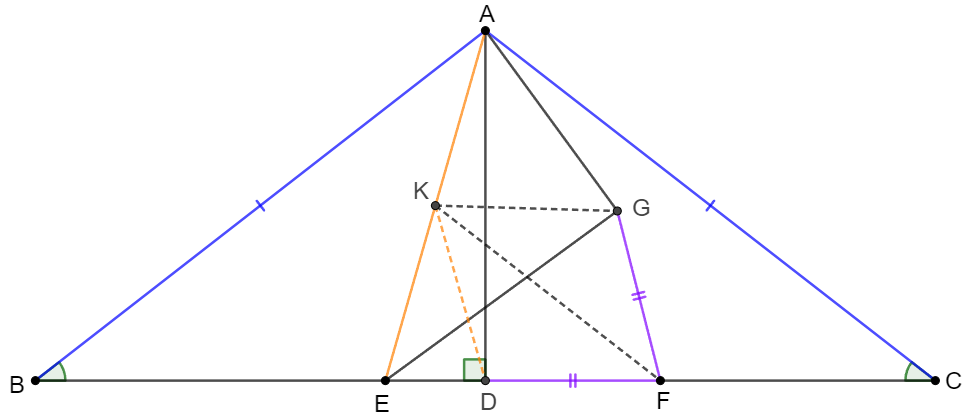
. \(\begin{multline}\nonumber \shoveleft \text{Let } K \text{ be the midpoint of }AE. \text{ Connect } DK, FK, GK\\ \shoveleft AD \perp BC, EK=AK \implies EK=DK=AK \\ \shoveleft EK=AK, EF=CF \implies FK \parallel AC \implies \angle{EFK}=\angle{C}\\ \shoveleft \implies \angle{GFK}=\angle{C}=\angle{DFK}, DF=GF \implies \triangle{DFK} \cong \triangle{GFK}\\ \shoveleft \implies GK=DK=EK=AK \implies AG \perp EG \blacksquare \end{multline}\)
06/26/2023
In a semicircle there are one right angle triangle and three squares like the figure. If the squares on both sides have area $a^2$ and $b^2$, find the area of the square in the middle.
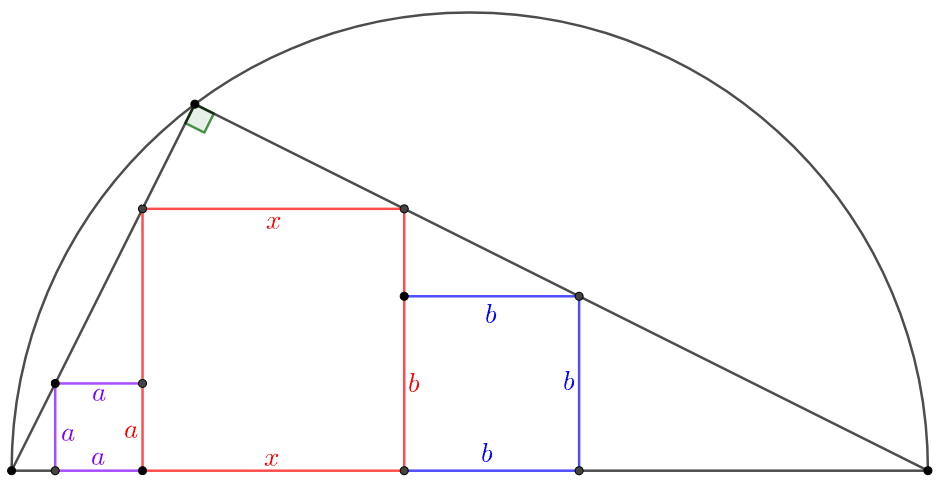
Solve:
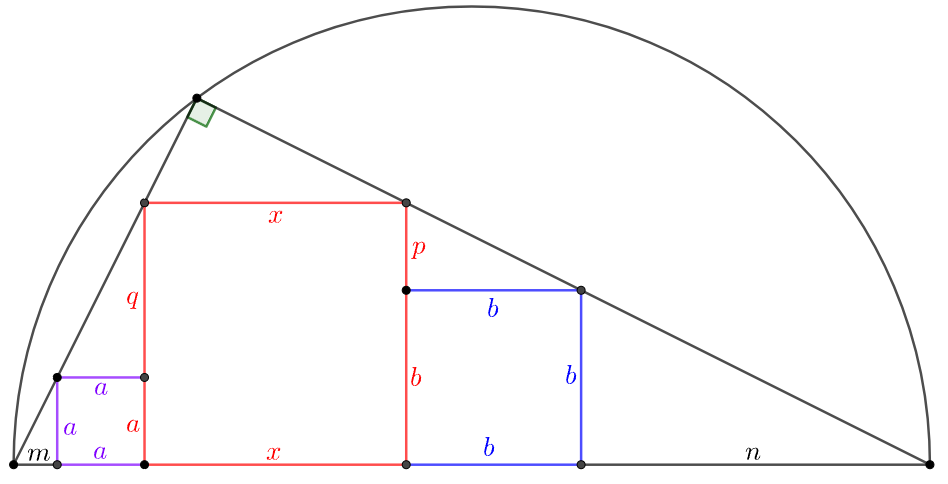
. \(\begin{multline}\nonumber \shoveleft \text{Assume the lengths of sides } m,n,p,q \text{ as above, by triangle similarity we know}\\ \shoveleft \dfrac{b}{n}=\dfrac{p}{b}=\dfrac{a}{q}=\dfrac{m}{a}\implies a^2=mq, b^2=np, ab=mn=pq\\ \shoveleft a+q=b+p \implies a+q=b+\dfrac{ab}{q} \implies q^2+(a-b)q-ab=0\\ \shoveleft \implies q=b \implies p=a \implies m=\dfrac{a^2}{b}, n=\dfrac{b^2}{a} \implies x=a+b\\ \shoveleft \implies S_x=\bbox[5px, border: 1px solid black]{(a+b)^2}\\\ \end{multline}\)
06/27/2023
$AD$ is bisector of $\angle{BAC}$ in $\triangle{ABC}$, $D$ is on $BC$, and $\angle{BAC}=60^{\circ},AB=2, BC=\sqrt{6}$, find $AD$.
Solve:
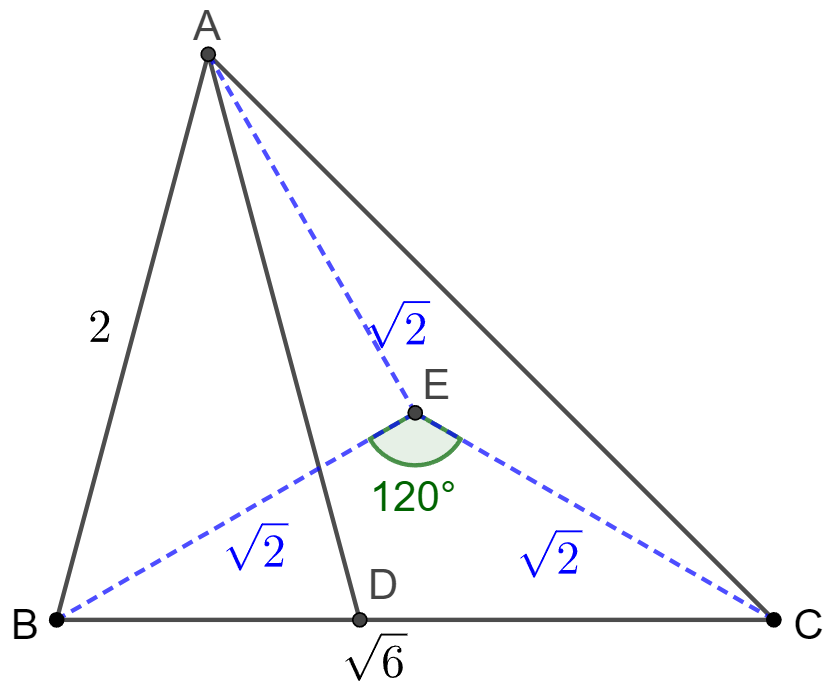
. \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ be the circumcenter of }\triangle{ABC} \implies AE=BE=CE\\ \shoveleft \angle{BAC}=60^{\circ} \implies \angle{BEC}=2\angle{BAC}=120^{\circ}\\ \shoveleft \implies BE=CE=AE=\dfrac{BC}{\sqrt{3}}=\dfrac{\sqrt{6}}{\sqrt{3}}=\sqrt{2}\\ \shoveleft AB=2 \implies \angle{AEB}=90^{\circ} \implies \angle{ACB}=\dfrac{\angle{AEB}}{2}=45^{\circ}\\ \shoveleft \implies \angle{ABC}=75^{\circ}, \text{ and we know }\angle{BAD}=\dfrac{\angle{BAC}}{2}=30^{\circ}\\ \shoveleft \implies \angle{ADB}=75^{\circ}\implies AD=AB=\boxed{2} \end{multline}\)