05/12/2023
In the semicircle, $\angle{BAC}=30^{\circ}, \overset{\huge\frown}{BC}=\overset{\huge\frown}{DE}$ Find the ratio the area of yellow colored zone to the area of the semicircle.
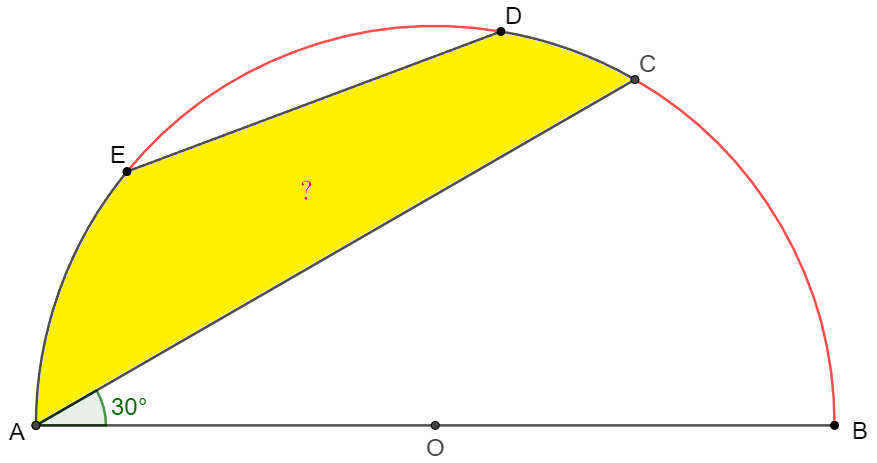
Solve:
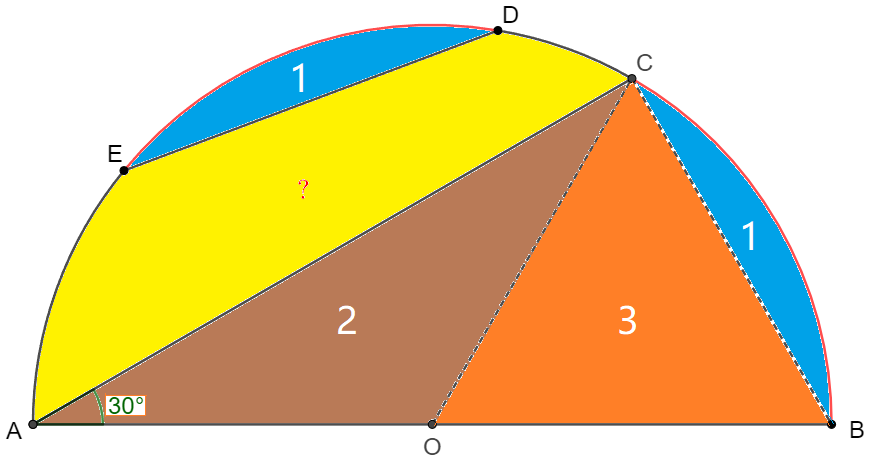
Connect $BC$ and $OC$,easy to see that the blue arc area $\overset{\huge\frown}{DE}$ equals to the blue arc area $\overset{\huge\frown}{BC}$, i.e., $S_1$, and $S_2=S_3$.
$\angle{BAC}=30^{\circ} \implies \angle{BOC}=60^{\circ} \implies S_1+S_3=S_1+S_2=\dfrac{1}{3}S_{\text{semicircle}}$
So we know the yellow-colored area is $1-\dfrac{2}{3}=\boxed{\dfrac{1}{3}}$ of the area of semicircle.
05/13/2023
Square $DEFG$ is inside of $\triangle{ABC}$ such that $D, E, F $ are on side $AB, BC, CA$ with $AD=7, DB=6, BE=EC, CF=2$.
(1) Prove $AD^2+BD^2=AF^2+CF^2$ and find $AF$
(2) Find $DE$.
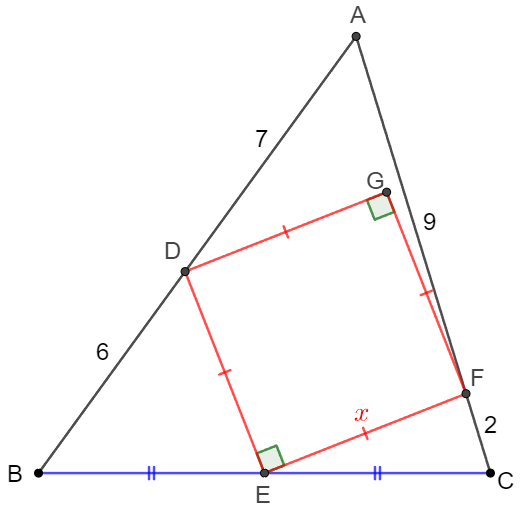
Prove and Solve:
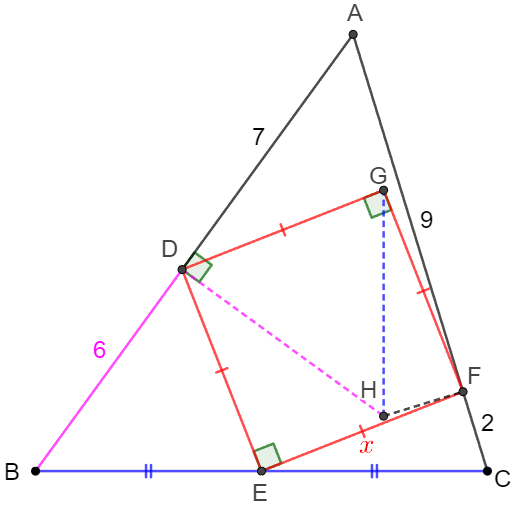
. \(\begin{multline}\nonumber \shoveleft \text{Rotate } B \text{ around } D \text{ to } H \text{ such that } BD=DH, DH \perp AB, \text{ connect } GH, FH\\ \shoveleft \implies \angle{BDE}=90^{\circ}-\angle{EDH}=\angle{HDG}, DE=DG \implies \triangle{BDE}\cong \triangle{HDG}\\ \shoveleft \implies BE=HG=CE, \angle{BED}=\angle{DGH} \implies \angle{CEF}=90^{\circ}-\angle{BED}=\angle{FGH}\\ \shoveleft \implies \triangle{CEF}\cong \triangle{HGF}\implies \angle{CFE}=\angle{GFH}\\ \shoveleft \implies \angle{EFH}+\angle{CFE}=\angle{EFH}+\angle{GFH}=90^{\circ} \implies HF\perp AC\\ \shoveleft AD^2+DH^2=AH^2=AF^2+FH^2 \implies AD^2+DB^2=AF^2+FC^2\blacksquare\\ \shoveleft \angle{ADH}=\angle{AFH}=90^{\circ} \implies ADHF \text{ are cyclic. Via Ptolemy's theorem]: }\\ \shoveleft AH \cdot DF = AD \cdot FH + AF \cdot DH \implies \sqrt{85} \cdot DF=14+54=68\\ \shoveleft \implies DF=\dfrac{68}{\sqrt{85}} \implies EF=x=\dfrac{68}{\sqrt{170}}=\bbox[5px, border: 1px solid black]{2\sqrt{\dfrac{34}{5}}} \end{multline}\)
05/14/2023
Inside a rectangle:
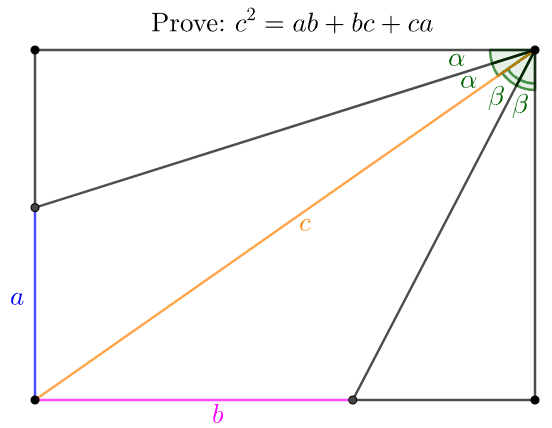
Prove 1:
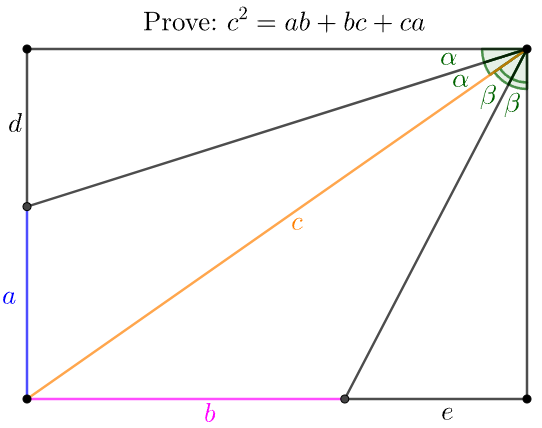\(\begin{multline}\nonumber
\shoveleft \text{Suppose } d, e \text{ as in diagram, from property of angle bisector:}\\
\shoveleft \dfrac{b+e}{d}=\dfrac{c}{a}, \dfrac{a+d}{e}=\dfrac{c}{b} \implies b+e=\dfrac{cd}{a}, a+d=\dfrac{ce}{b}\\
\shoveleft \implies d=\dfrac{b+e}{c}a, e=\dfrac{a+d}{c}b \implies \dfrac{d}{a}=\dfrac{a+c}{c^2-ab}b, \dfrac{e}{b}=\dfrac{b+c}{c^2-ab}a\\
\shoveleft c^2=(a+d)^2+(b+e)^2=c^2(\dfrac{d^2}{a^2}+\dfrac{e^2}{b^2})=c^2\dfrac{b^2(a+c)^2+a^2(b+c)^2}{(c^2-ab)^2}\\
\shoveleft \implies (c^2-ab)^2=b^2(a+c)^2+a^2(b+c)^2\\
\shoveleft \implies c^4=a^2b^2+b^2c^2+c^2a^2+2ab^c+2a^bc+2abc^2\\
\shoveleft \implies c^4=(ab+bc+ca)^2 \implies c^2=ab+bc+ca\blacksquare
\end{multline}\)
Prove 2:
\(\begin{multline}\nonumber
\shoveleft \text{Suppose } d, e \text{ as in diagram, from property of angle bisector:}\\
\shoveleft \dfrac{d}{b+e}=\dfrac{a}{c}=tan (\alpha), \dfrac{e}{a+d}=\dfrac{b}{c}=tan(\beta)\\
\shoveleft \alpha+\beta=45^{\circ} \implies tan(\alpha + \beta)=1=\dfrac{tan(\alpha)+tan(\beta)}{1-tan(\alpha)tan(\beta)}\\
\shoveleft \implies \dfrac{\dfrac{a}{c}+\dfrac{b}{c}}{1-\dfrac{ab}{c^2}}=1 \implies \dfrac{ac+bc}{c^2-ab}=1\implies c^2=ab+bc+ca\blacksquare
\end{multline}\)
Prove 3:
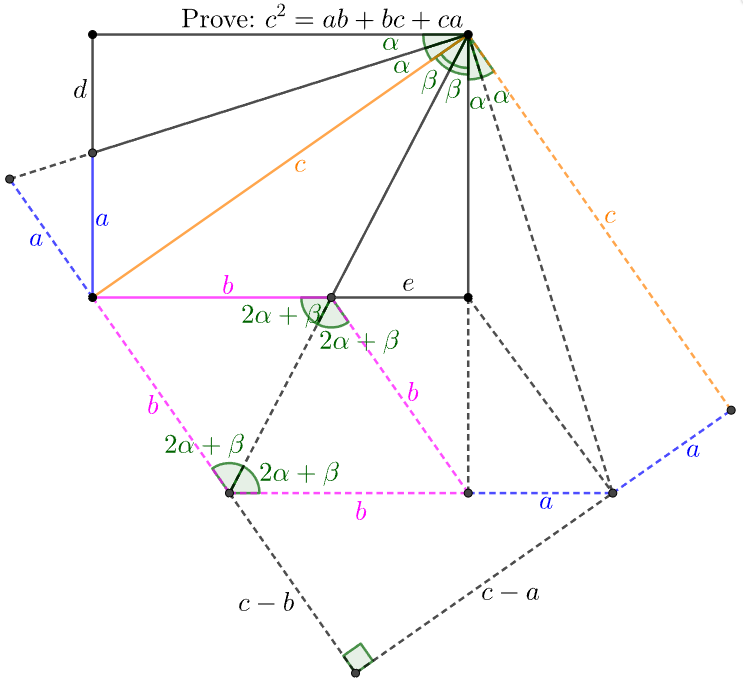\(\begin{multline}\nonumber
\shoveleft \text{From the dialgram to see } (a+b)^2=(c-a)^+(c-b)^2\\
\shoveleft \implies c^2=ab+bc+ca\blacksquare
\end{multline}\)
Prove 4:
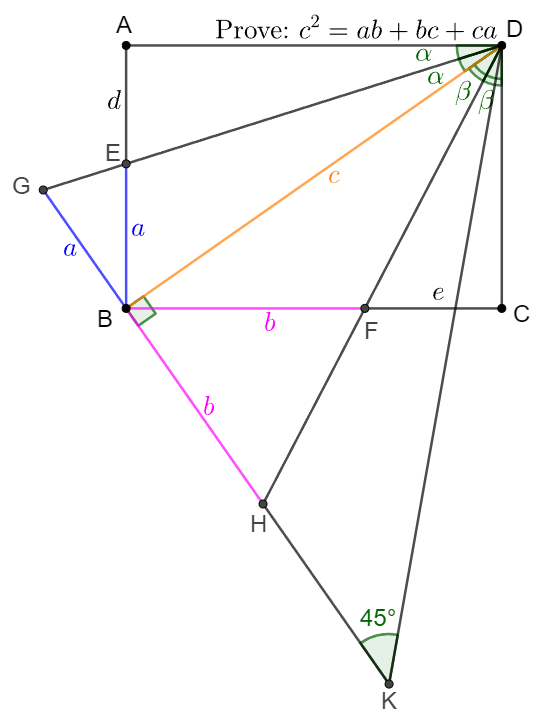
. \(\begin{multline}\nonumber \shoveleft \text{Make } BK\perp BD \text{ and } BK=BD, \text{ extend } KB, DE \text{ and intersect at }G\\ \shoveleft \angle{BGD}=90^{\circ}-\alpha=\angle{AED}=\angle{BEG}\implies BG=BE=a\\ \shoveleft \angle{BHD}=90^{\circ}-\beta=\angle{CFD}=\angle{BFH}\implies BH=BF=b\\ \shoveleft \implies \angle{DKG}=45^{\circ}=\angle{GDH} \implies \triangle{GDH}\sim\triangle{GKD}\\ \shoveleft \implies \dfrac{GH}{GD}=\dfrac{GD}{GK} \implies \dfrac{a+b}{\sqrt{a^2+c^2}}-\dfrac{\sqrt{a^2+c^2}}{a+c} \implies c^2=ab+bc+ca\blacksquare \end{multline}\)
05/15/2023
Suppose three shaded areas in the triangle has area as $a, b, c$, find the area of the solid colored small triangle.
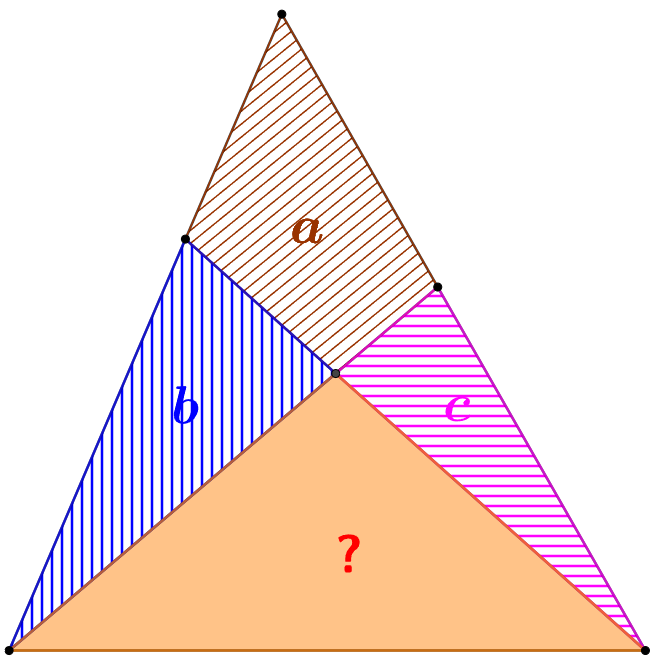
Solve:
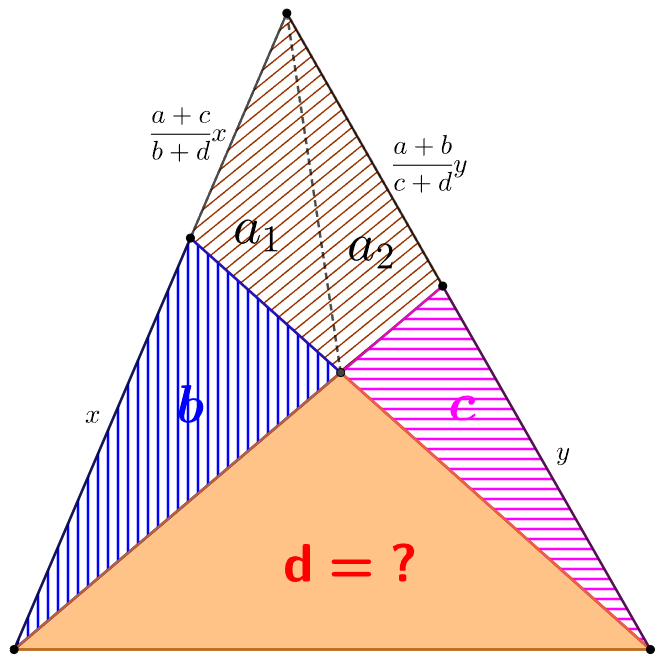
. \(\begin{multline}\nonumber \shoveleft \text{Suppose in the diagram }a_1+a_2=a, \text{ then}\\ \shoveleft \dfrac{a_1}{b}=\dfrac{a+c}{b+d} \implies a_1=\dfrac{a+c}{b+d}b\\ \shoveleft \dfrac{a_2}{c}=\dfrac{a+b}{c+d} \implies a_2=\dfrac{a+b}{c+d}c\\ \shoveleft \dfrac{a+c}{b+d}b + \dfrac{a+b}{c+d}c = a\\ \shoveleft \implies ad^2-2bcd-bc(a+b+c)=0\\ \shoveleft \implies d=\bbox[5px, border: 1px solid black]{\dfrac{bc+\sqrt{bc(a^2+ab+bc+ca)}}{a}} \end{multline}\)
05/16/2023
$\triangle{ABC}$ is equilateral, $AE\perp BC$, $\angle{ABM}=15^{\circ}$, $AE $ and $BM$ intersect at $N$, the circle pass through $ABM$ and $AE$ intersect at $P$. Prove that $AN=NP$.
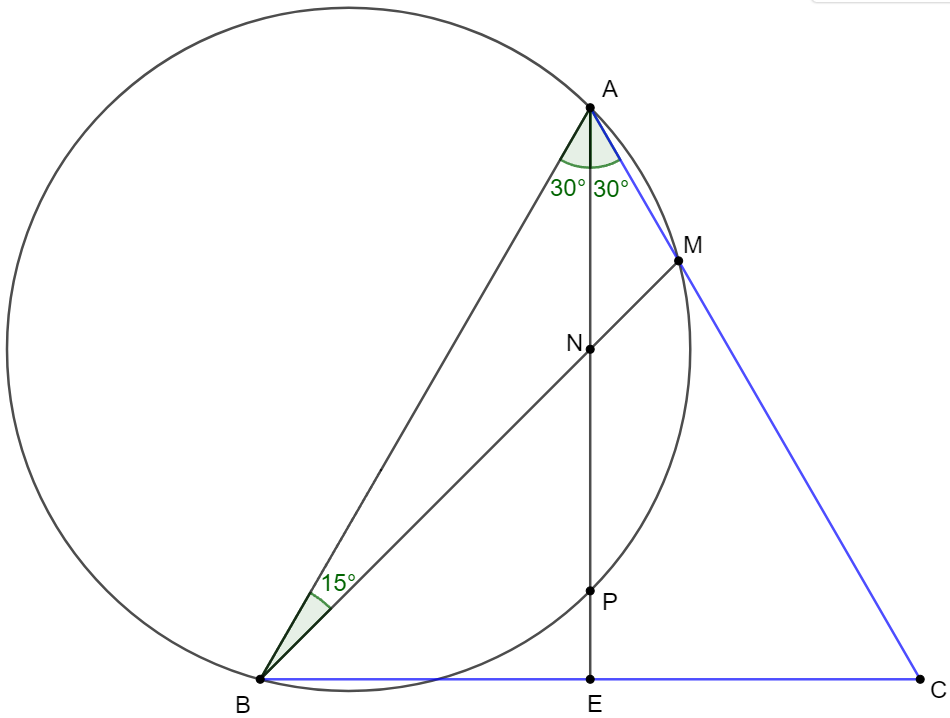
Prove 1:
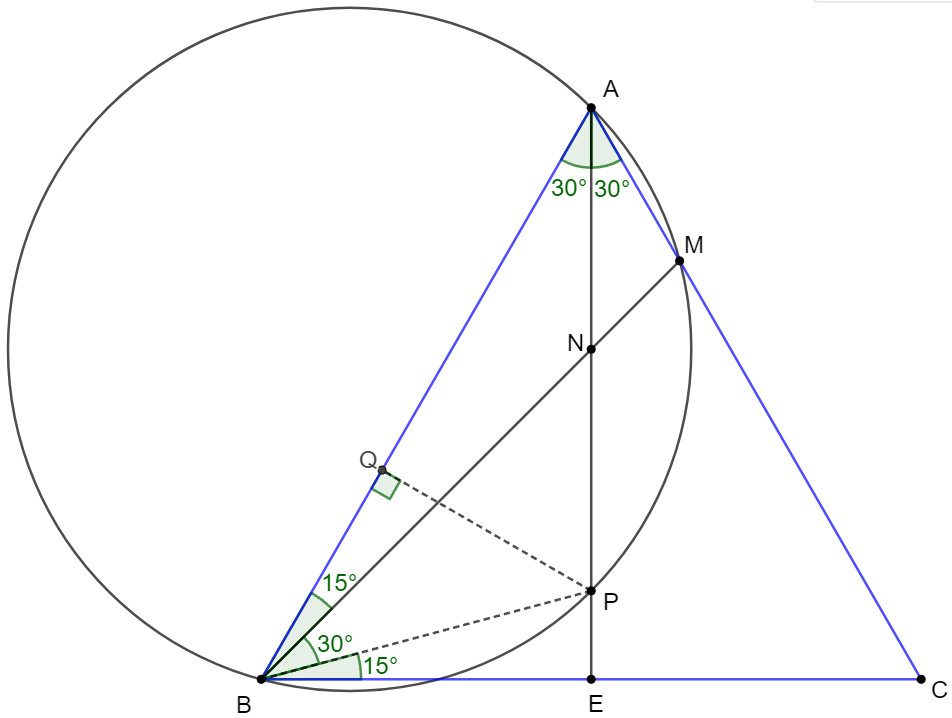
. \(\begin{multline}\nonumber \shoveleft \text{Connect }BP, \text{ make } Q \text{ on }AB \text{ such that } PQ\perp AB.\\ \shoveleft \angle{NBE}=60^{\circ}-15^{\circ}=45^{\circ} \implies NE=BE=\dfrac{1}{2}BC\\ \shoveleft AE=\dfrac{\sqrt{3}}{2}BC \implies AN=AE-NE=\dfrac{\sqrt{3}-1}{2}BC\\ \shoveleft \angle{PAQ}=30^{\circ}, \angle{PBM}=\angle{PAM}=30^{\circ} \implies \angle{PBQ}=45^{\circ}\\ \shoveleft PQ \perp AB\implies AP=2PQ=2BQ, QA=\sqrt{3}PQ \\ \shoveleft \implies AB=BQ+QA=BQ+\sqrt{3}BQ=BC \implies BQ=\dfrac{1}{\sqrt{3}+1}BC\\ \shoveleft \implies AP=2BQ=\dfrac{2}{\sqrt{3}+1}BC=(\sqrt{3}-1)BC\\ \shoveleft \implies AP=2AN\implies AN=NP\blacksquare \end{multline}\) Prove 2:
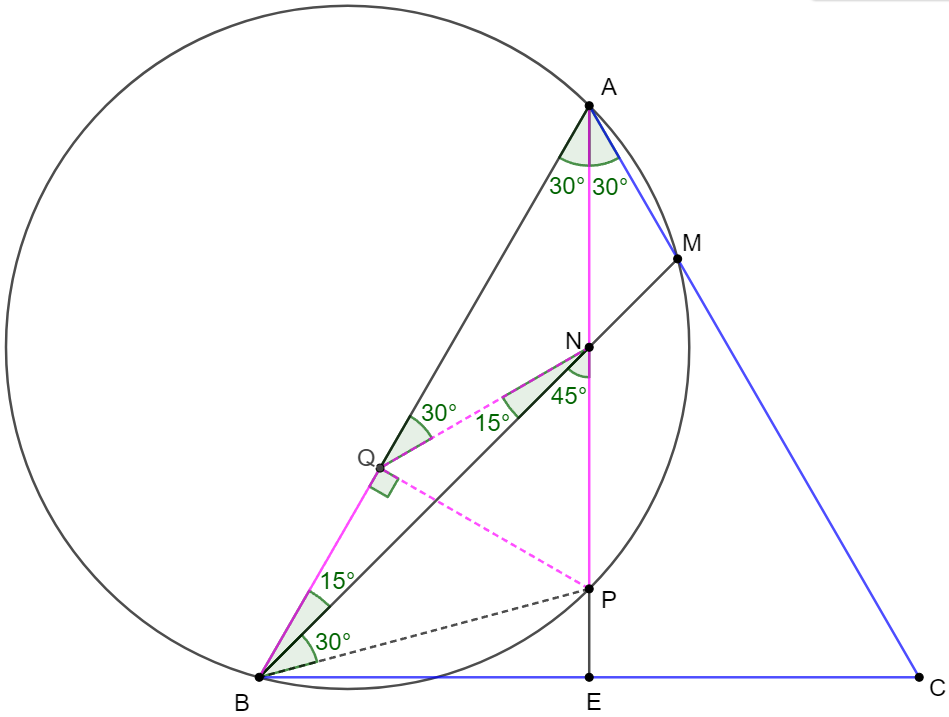
. \(\begin{multline}\nonumber \shoveleft \text{Connect }BP, \text{ make } Q \text{ on }AB \text{ such that } PQ\perp AB, \text{ connect } PQ, NQ\\ \shoveleft \angle{BNP}=15^{\circ}+30^{\circ}=45^{\circ}, \angle{PBM}=\angle{PAM}=30^{\circ}\\ \shoveleft \implies \angle{PBQ}=45^{\circ}\implies BQ=PQ, \angle{BQP}=2\angle{BNP}\\ \shoveleft \implies Q \text{ is circumcenter of } \triangle{BNP} \implies BQ=PQ=NQ\\ \shoveleft \implies \angle{BNQ}=\angle{NBQ}=15^{\circ} \implies \angle{PNQ}=60^{\circ}, \angle{NQA}=30^{\circ}=\angle{QAN}\\ \shoveleft \implies AN=NQ, \triangle{PNQ} \text{ is equilateral} \implies NP=NQ \implies AN=NP\blacksquare\\ \end{multline}\)
05/17/2023
In quadrilateral $ABCD$, $BC=6,CD=3, DA=5, BC\perp CD, \angle{DAB}=\angle{CBA}$. Find $AB$.
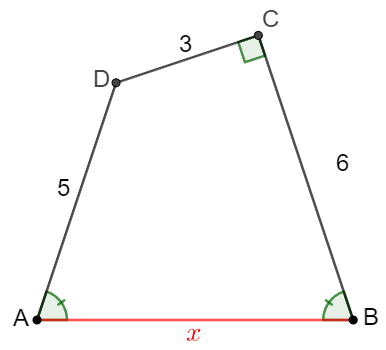
Solve:
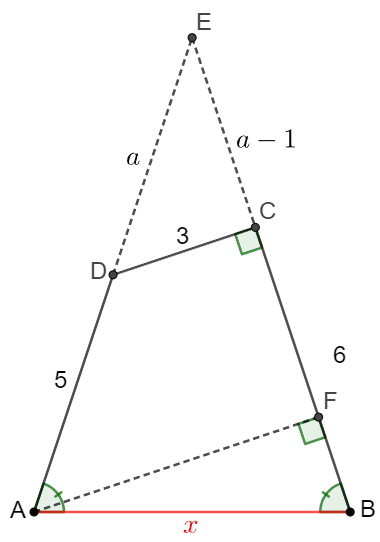
. \(\begin{multline}\nonumber \shoveleft \text{Extend } AD, BC \text{ and intersect at } E. \text{ Make } F \text{ on } BC \text{ such that } AF\perp BC.\\ \shoveleft \angle{DAB} =\angle{CBA} \implies EA=EB. \text{ Suppose } DE=a \implies CE=a-1 \\ \shoveleft \implies a^2=(a-1)^2+3^2\implies a=5 \implies \dfrac{AF}{CD}=\dfrac{EF}{EC}=\dfrac{AE}{ED}=2\\ \shoveleft \implies AF=6, EF=8 \implies BF=2\\ \shoveleft \implies AB=x=\sqrt{AF^2+BF^2}=\sqrt{6^2+2^2}=\bbox[5px, border: 1px solid black]{2\sqrt{10}} \end{multline}\)
05/18/2023
Points $E, F$ are midpoint of side $BC, AB$ in square. $AE, DF$ intersects at $G$. Prove $CD=CG$.
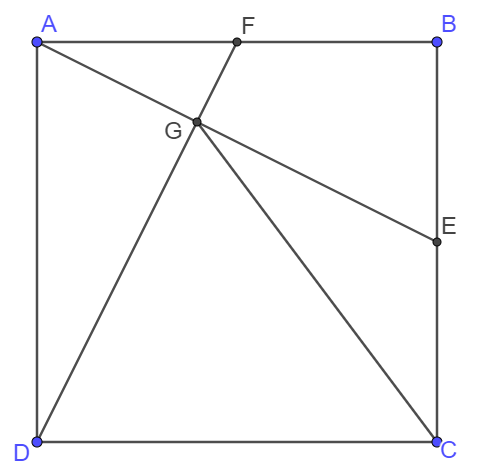
Prove:
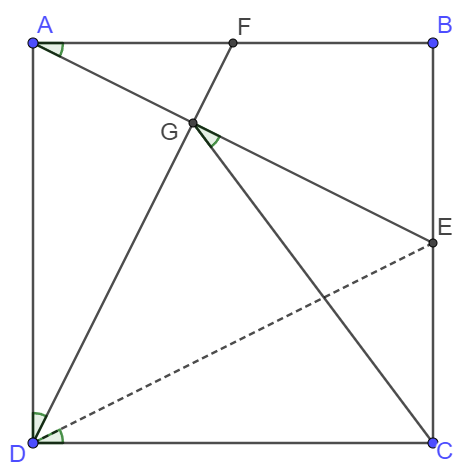
. \(\begin{multline}\nonumber \shoveleft \text{Connect }DE. E, F \text{are midpoints of } BC, AB \implies \angle{CDE}=\angle{ADF}=\angle{BAE}\\ \shoveleft \implies \angle{DAE}+\angle{ADF}=\angle{DAE}+\angle{BAE}=90^{\circ} \implies AE \perp DF\\ \shoveleft \implies CDGE \text{ are cyclic} \implies \angle{CGE}=\angle{CDE}=\angle{ADF}\\ \shoveleft \implies \angle{CDG}=\angle{CGD} \implies CD=CG\blacksquare \end{multline}\)
05/21/2023
The distances of point $E$ inside equilateral triangle $\triangle{ABC}$ to the side $BC, CA, AB$ are $a, b, c$. Find $S_1 : S_2 : S_3$.
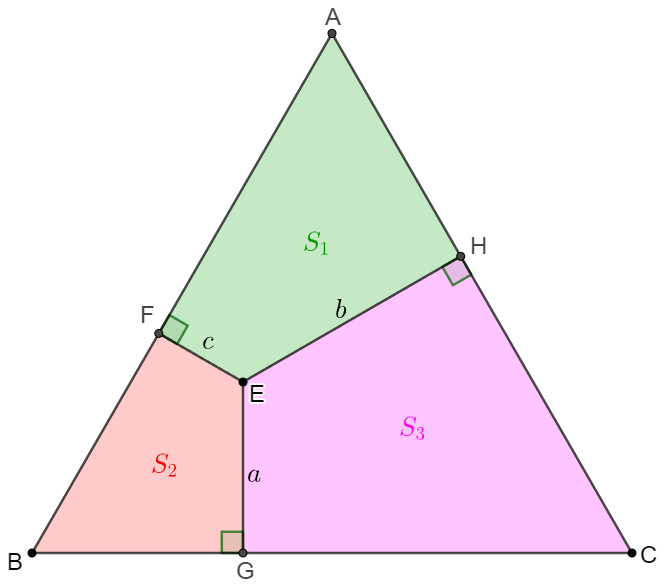
Solve:
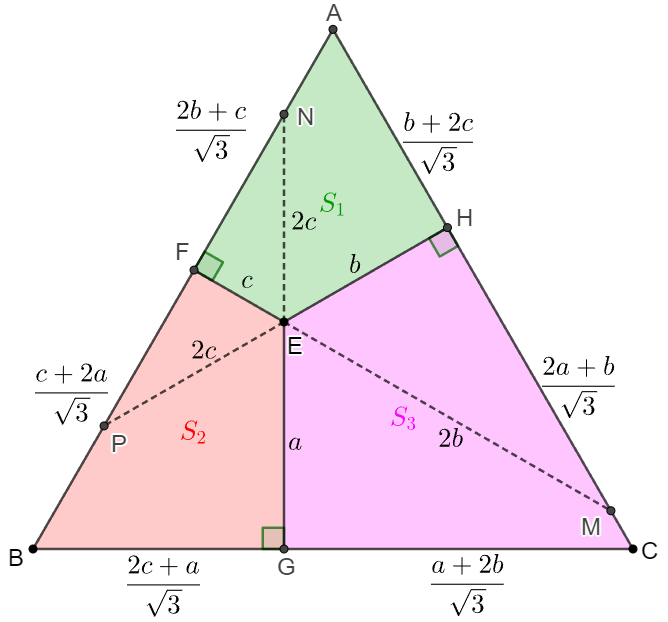
. \(\begin{multline}\nonumber \shoveleft \text{Let } AB = k, \text{ then }[ABC]=\dfrac{\sqrt{3}}{4}k^2 =[BEC]+[CEA]+[AEB]\\ \shoveleft =\dfrac{a}{2}k+\dfrac{b}{2}k+\dfrac{c}{2}k \implies a+b+c=\dfrac{\sqrt{3}}{2}k \implies k=\dfrac{2(a+b+c)}{\sqrt{3}}\\ \shoveleft \text{Extend } FE, GE, HE \text{ to meet the sides of } \triangle{ABC} \text{ at } M, N, P\\ \shoveleft \text{The following diagram gives the situation when } a>b>c, \\ \shoveleft \text{the same result can be got in other situations as:}\\ \shoveleft \triangle{EHM}\sim\triangle{FMA}\implies EM=2EH=2b \implies FM=2b+c\\ \shoveleft \implies \bbox[5px, border: 2px dotted black]{AF=\dfrac{2b+c}{\sqrt{3}}} \implies \bbox[5px, border: 2px dotted black]{BF=\dfrac{2a+2b+2c-(2b+c)}{\sqrt{3}}=\dfrac{c+2a}{\sqrt{3}}}\\ \shoveleft \triangle{EFP}\sim\triangle{AHP} \implies FP=2EF=2c \implies HP=b+2c\\ \shoveleft \implies \bbox[5px, border: 2px dotted black]{AH=\dfrac{b+2c}{\sqrt{3}}} \implies \bbox[5px, border: 2px dotted black]{CH=\dfrac{2a+2b+2c-(b+2c)}{\sqrt{3}} = \dfrac{2a+b}{\sqrt{3}}}\\ \shoveleft \triangle{EFN}\sim\triangle{BNG} \implies EN=2EF=2c \implies NG=2c+a\\ \shoveleft \implies \bbox[5px, border: 2px dotted black]{BG=\dfrac{2c+a}{\sqrt{3}}} \implies \bbox[5px, border: 2px dotted black]{CG=\dfrac{2a+2b+2c-(2c+a)}{\sqrt{3}} = \dfrac{a+2b}{\sqrt{3}}}\\ \shoveleft \implies S_1=\dfrac{b\cdot AH + c\cdot AF}{2}=\dfrac{(2b+c)c+(b+2c)b}{2\sqrt{3}}=\dfrac{b^2+4bc+c^2}{2\sqrt{3}}\\ \shoveleft S_2=\dfrac{c\cdot BF + a\cdot BG}{2}=\dfrac{(c+2a)c+(2c+a)a}{2\sqrt{3}}=\dfrac{c^2+4ac+a^2}{2\sqrt{3}}\\ \shoveleft S_3=\dfrac{a\cdot CG + b\cdot CH}{2}=\dfrac{(a+2b)a+(2a+b)b}{2\sqrt{3}}=\dfrac{a^2+4ab+b^2}{2\sqrt{3}}\\ \shoveleft \implies S_1 : S_2 : S_3 = \bbox[5px, border: 1px solid black]{(b^2+4bc+c^2) : (c^2+4ac+a^2) : (a^2+4ab+b^2)} \end{multline}\)
05/22/2023
Right angle triangle $\triangle{ABC}$ has $BC=\sqrt{2}$. Point $D$ is inside the triangle such that $AD=\sqrt{3}, CD=1, \angle{ADC}=120^{\circ}$. Find $\angle{BCD}$.
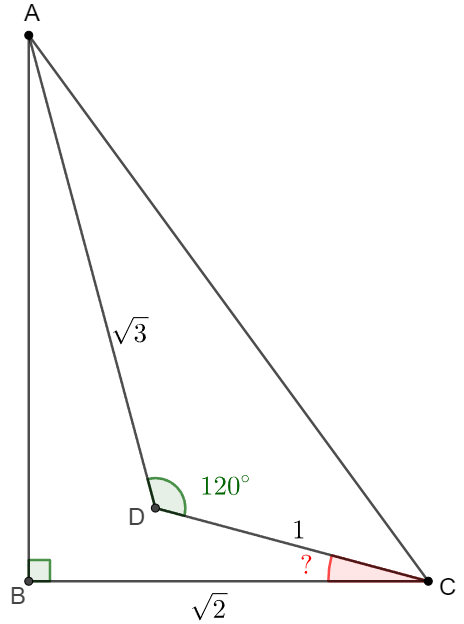
Solve:
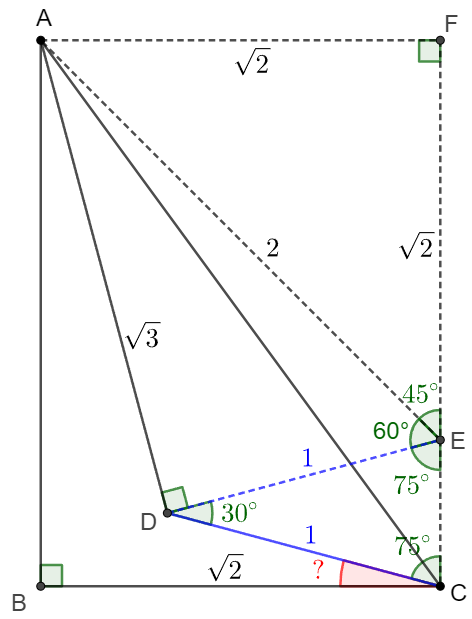
. \(\begin{multline}\nonumber \shoveleft \text{Make } DE\perp AD \text{ and } DE=DC=1, \text{ connect } AE, CE.\\ \shoveleft \implies AE=2, \angle{CDE}=30^{\circ} \implies \angle{DEC}=\angle{DCE}=75^{\circ}\\ \shoveleft \text{Extend } CE \text{ to } F \text{ such that } AF \perp CF \implies \angle{AEF}=45^{\circ}\\ \shoveleft \implies EF=AF=\sqrt{2}=BC \implies \triangle{ABC} \cong \triangle{CFA}\\ \shoveleft \implies \angle{ACB}+\angle{ACF}=\angle{ACB}+\angle{CAB}=90^{\circ}\\ \shoveleft \implies \angle{BCD}=90^{\circ}-\angle{DCE}=\bbox[5px, border: 1px solid black]{15^{\circ}} \end{multline}\)
05/28/2023
[2010 AMC 12A Problem 23] The number obtained from the last two nonzero digits of $90!$ is equal to $N$. What is $N$?
Solve 1: \(\begin{multline}\nonumber \shoveleft 90! \text{ is divisible by } 2^{\Bigl\lfloor\dfrac{90}{2}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{2^2}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{2^3}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{2^4}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{2^5}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{2^6}\Bigr\rfloor}=2^{45+22+11+5+2+1}=2^{86}.\\ \shoveleft \text{Similarly, } 90! \text{ is divisible by } 5^{\Bigl\lfloor\dfrac{90}{5}\Bigr\rfloor+\Bigl\lfloor\dfrac{90}{5^2}\Bigr\rfloor} =5^{18+3}=5^{21}. \text{So } 90! \text{ is divisible by } 10^{21}. \\ \shoveleft \text{ Let } A=\dfrac{90!}{5^{21}}, A \equiv C \text{ (mod 100)}, A \equiv B \text{ (mod 25)}\\ \shoveleft \implies C=B \text{ or } C=B+25 \text{ or } C=B+50 \text{ or } C=B+75\\ \shoveleft \text{And we know } C \text { is divisible by 4}.\\ \shoveleft \text{Among } B, B+25, B+50, B+75, \text{ there is only one number is divisible by 4.}\\ \shoveleft \text{Now we check } A=\dfrac{90!}{5^{21}} \equiv B (\text{mod }25):\\ \shoveleft A =(1\cdot 2\cdot 3\cdot 4)(6 \cdot 7\cdot 8\cdot 9)...(86 \cdot 87 \cdot 88 \cdot 89)\\ \shoveright \text{<-- } 4 \times \lceil \dfrac{90}{5} \rceil = 4 \times 18=72\text{ numbers are not multiples of 5}\\ \shoveleft \cdot (1 \cdot 2 \cdot 3 \cdot 4)(6 \cdot 7 \cdot 8\cdot 9)...(16 \cdot 17 \cdot 18 \cdot 19)\\ \shoveright \text{<-- } 4 \times \lceil \dfrac{18}{5} \rceil - 1 = 4 \times 4 - 1 = 15 \text{ multiples of 5 and not 25 after divided by 5}\\ \shoveleft \cdot (1 \cdot 2 \cdot 3)\\ \shoveright \text{<-- } 4 \times \lceil \dfrac{4}{5} \rceil - 1 = 4 \times 1 -1 = 3 \text{ multiples of 25 after divided by 25}\\ \shoveleft 4! \equiv -1 \text{ (mod 25)}\\ \shoveleft (5k+1)(5k+2)(5k+3)(5k+4) \equiv (15k+2)(10k+12) \equiv 24 \equiv -1 \text{ (mod 25)}\\ \shoveleft \implies \text{The four-number-product starting with } 1, 6, 11, 16, 21, 26, 31, 36, 41, 46,\\ \shoveleft 51, 56, 61, 66, 71, 76, 81,86 \equiv -1 \text{ (mod 25)} \implies (-1)^{18} \equiv 1 \text{ (mode 25)}\\ \shoveleft \text{In the remainings, } 5\cdot10\cdot15\cdot20=5^4(4!),30\cdot35\cdot40\cdot45=5^4(6\cdot7\cdot8\cdot9)\\ \shoveleft 55\cdot60\cdot65\cdot70=5^4(11\cdot12\cdot13\cdot14), 80\cdot85\cdot90\cdot95=5^4(16\cdot17\cdot18\cdot19) \cdot (19)^{-1}\\ \shoveleft \text{Since all 5s are removed, all the items in bracket} \equiv -1 \text{ (mod 25)}\\ \shoveleft \text{so they contribute } (-1)^4 \equiv 1 \text{ (mod 25)} \text{ but 95 is missed so we get }\\ \shoveleft (19)^{-1} \equiv 4 \text{ (mod 25)} \text { since } 19\cdot4 \equiv 1 \text{ (mod 25)} \implies B=4\\ \shoveleft \implies A=(-1)^{18}\cdot 4 \cdot 6 = 24 \text{ (mode 25)}\\ \shoveleft \text{Now consider }\dfrac{A}{2^{21}} \text{ (mod 25)}:\\ \shoveleft 2^{10}=1024 \equiv -1 \text{ (mod 25)} \implies 2^{21} \equiv (-1)^2 \cdot 2 \equiv 2 \text{ (mod 25)}\\ \shoveleft \implies \dfrac{A}{10^{21}} \equiv \dfrac{24}{2} \equiv 12 \text{ (mod 25)}\\ \shoveleft \dfrac{A}{10^{21}} \equiv 0 \text{ (mod 4)} \implies \dfrac{A}{10^{21}} \equiv 12 \text{ (mod 100)} \implies N=\bbox[5px, border: 1px solid black]{12} \end{multline}\)
Solve 2: \(\begin{multline}\nonumber \shoveleft 90! \text{ has exactly }\Bigl\lfloor \dfrac{90}{5} \Bigr\rfloor + \Bigl\lfloor \dfrac{90}{5^2} \Bigr\rfloor = 21 \text{ factors of 5} \text{ Let } A= \dfrac{90!}{2^{21}\cdot 5^{21}}\\ \shoveleft \text{Easy to see } A \equiv 0 \text{ (mod 4), so we only ned to consider A (mod 25)}:\\ \shoveleft (5n+a)(5n-a) \equiv -a^2 \text{ (mod 25)} \implies\\ \shoveleft (10a+1)(10a+2)(10a+3)(10a+4)(10a+6)(10a+7)(10a+8)(10a+9)\\ \shoveleft \equiv (-1)(-4)(-9)(-16)\equiv 576 \equiv 1 \text{ (mod 25)} \implies 90!\equiv 5 \cdot 10 \cdot 15 \cdot ... \cdot 90 \text{ (mod 25)}\\ \shoveleft 10 \cdot 20 \cdot 30 \cdot...\cdot90 \text{ removing 5s gets } 1 \cdot 2 \cdot 3 \cdot 4 \cdot 1 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot 2^8\equiv 1 \cdot 2^8 \equiv 6 \text{ (mod 25)}\\ \shoveleft 5 \cdot 15 \cdot 25 \cdot 35 \cdot 45 \cdot 50 \cdot 55 \cdot 65 \cdot 75 \cdot 85 \text{ gets } 1 \cdot 3 \cdot 1 \cdot 7 \cdot 9 \cdot 2 \cdot 11 \cdot 13 \cdot 3 \cdot 17 \equiv 4 \text{ (mode 25)}\\ \shoveleft \implies \dfrac{90!}{5^{21}} \equiv 24 \text{ (mod 25)}, \text{ and } 2^{21}=2\cdot 1024^2 \equiv 2 \cdot(-1)^2 \equiv 2 \text{ (mod 25)}\\ \shoveleft \implies A \equiv \dfrac{24}{2} \equiv{12} \text{ (mod 5)}. \text{ Because 12 is also a multiple f 4, we can utilize the }\\ \shoveleft \text{Chinese Remainder Theorem to show that } A \equiv {12} \text{ (mod 100)} \implies N= \bbox[5px, border: 1px solid black]{12} \end{multline}\)