04/14/2023

In quadrilateral $ABCD$, $\angle{ABD}=20^{\circ}, \angle{CBD}=10^{\circ}, \angle{ADB}=\angle{CDB}=60^{\circ}$, find $\angle{ACB}$

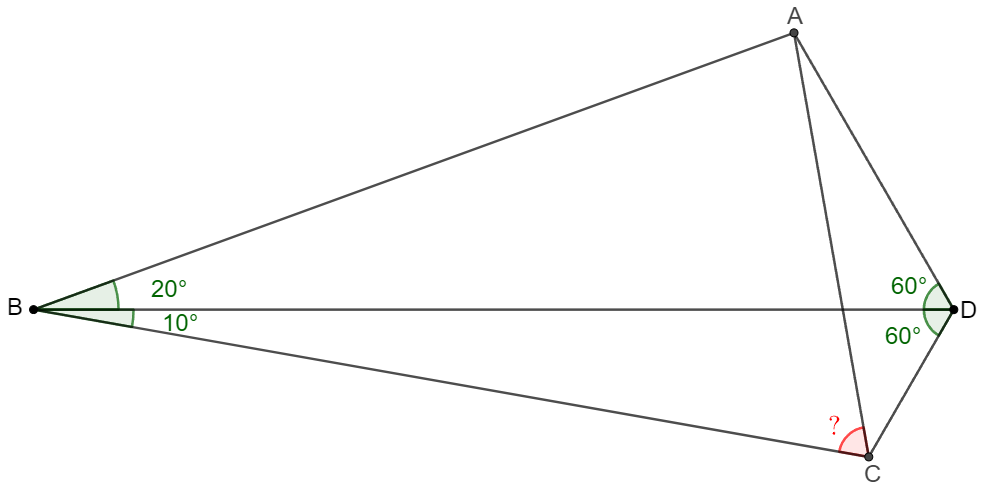
Solve:

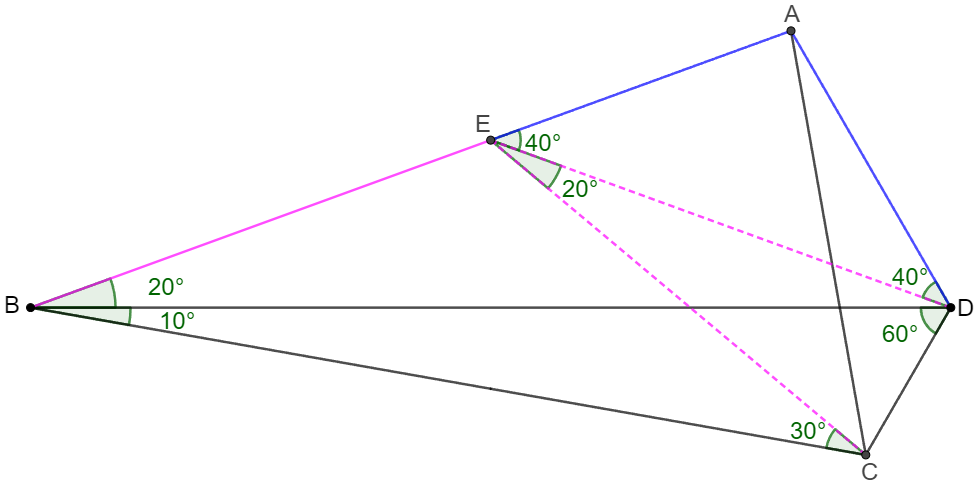\(\begin{multline}\nonumber \shoveleft \text{Make } E \text{ on } AB \text{ such that } \angle{BCE}=\angle{EBC}=30^{\circ}\\ \shoveleft \implies BE=CE, \angle{BEC}=120^{\circ}=2\angle{BDC}\\ \shoveleft \implies E \text{ is the circumcenter of } \triangle{BCD}\\ \shoveleft \implies \angle{CED}=2\angle{CBD}=20^{\circ}, BE=CE=DE \\ \shoveleft \implies \angle{EDB}=\angle{EBD}=20^{\circ} \implies \angle{ADE}=40^{\circ}\\ \shoveleft \implies \angle{BEC}=120^{\circ}=\angle{ADB}+\angle{BDC}\\ \shoveleft \implies AECD \text{ is cyclic} \implies \angle{ACE}=\angle{ADE}=40^{\circ}\\ \shoveleft \implies \angle{ACB}=40^{\circ}+30^{\circ}=\bbox[5px, border: 1px solid black]{70^{\circ}} \end{multline}\)