03/10/2023
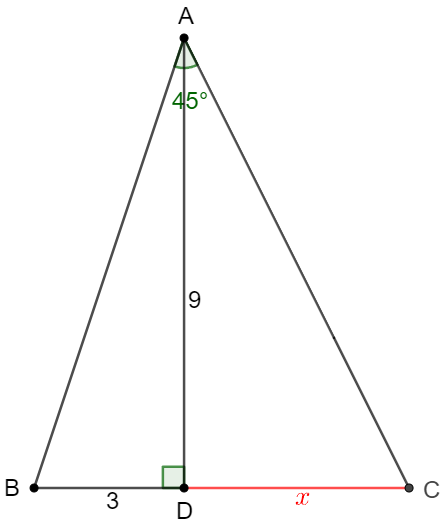
In $\triangle{ABC}$, $\angle{BAC}=45^{\circ}, AD \perp BC, BD=3, AD=9$, find $CD$ .
Solve 1:
 \(\begin{multline} \nonumber
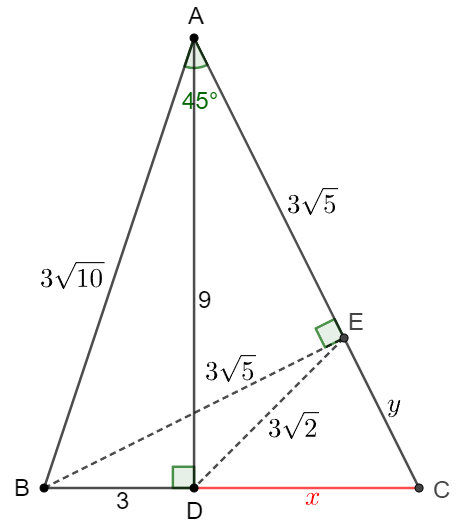
\shoveleft \text{ Make } BE\perp AC, \text{ connect } DE, \text{ easy to see }\\
\shoveleft AB=3\sqrt{10}, AE=BE=\dfrac{AB}{\sqrt{2}}=3\sqrt{5}\\
\shoveleft \text{By the Ptolemy's theorem we know: }\\
\shoveleft AB \cdot DE+ BD \cdot AE = BE \cdot AD\\
\shoveleft \implies DE=3\sqrt{2}, \text{ let } CD=x, CE=y\\
\shoveleft \triangle{CDE}\sim\triangle{CAB} \implies \dfrac{DE}{AB}=\dfrac{CD}{CA}=\dfrac{CE}{CB}\\
\shoveleft \implies \dfrac{1}{\sqrt{5}}=\dfrac{x}{3\sqrt{5}+y}=\dfrac{y}{3+x}\\
\shoveleft \implies y=\dfrac{3\sqrt{5}}{2}, x=\bbox[5px, border: 1px solid black]{\dfrac{9}{2}}
\end{multline}\)
Solve 2:
\(\begin{multline}\nonumber
\shoveleft \text{ Make } BE\perp AC, \text{ connect } DE, \text{ easy to see }\\
\shoveleft AB=3\sqrt{10}, AE=BE=\dfrac{AB}{\sqrt{2}}=3\sqrt{5}\\
\shoveleft \implies [ABC]=\dfrac{AD \cdot BC}{2}=\dfrac{9(3+CD)}{2}\\
\shoveleft =\dfrac{BE \cdot AC}{2}=\dfrac{3\sqrt{5}(\sqrt{81+CD^2})}{2}\\
\shoveleft \implies CD=\bbox[5px, border: 1px solid black]{\dfrac{9}{2}}
\end{multline}\)
\(\begin{multline} \nonumber
\shoveleft \text{ Make } BE\perp AC, \text{ connect } DE, \text{ easy to see }\\
\shoveleft AB=3\sqrt{10}, AE=BE=\dfrac{AB}{\sqrt{2}}=3\sqrt{5}\\
\shoveleft \text{By the Ptolemy's theorem we know: }\\
\shoveleft AB \cdot DE+ BD \cdot AE = BE \cdot AD\\
\shoveleft \implies DE=3\sqrt{2}, \text{ let } CD=x, CE=y\\
\shoveleft \triangle{CDE}\sim\triangle{CAB} \implies \dfrac{DE}{AB}=\dfrac{CD}{CA}=\dfrac{CE}{CB}\\
\shoveleft \implies \dfrac{1}{\sqrt{5}}=\dfrac{x}{3\sqrt{5}+y}=\dfrac{y}{3+x}\\
\shoveleft \implies y=\dfrac{3\sqrt{5}}{2}, x=\bbox[5px, border: 1px solid black]{\dfrac{9}{2}}
\end{multline}\)
Solve 2:
\(\begin{multline}\nonumber
\shoveleft \text{ Make } BE\perp AC, \text{ connect } DE, \text{ easy to see }\\
\shoveleft AB=3\sqrt{10}, AE=BE=\dfrac{AB}{\sqrt{2}}=3\sqrt{5}\\
\shoveleft \implies [ABC]=\dfrac{AD \cdot BC}{2}=\dfrac{9(3+CD)}{2}\\
\shoveleft =\dfrac{BE \cdot AC}{2}=\dfrac{3\sqrt{5}(\sqrt{81+CD^2})}{2}\\
\shoveleft \implies CD=\bbox[5px, border: 1px solid black]{\dfrac{9}{2}}
\end{multline}\)