02/10/2023
$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=\angle{CBD}=20^{\circ}, \angle{ACD}=30^{\circ}, \angle{BCD}=10^{\circ}$, find $\angle{CAD}$
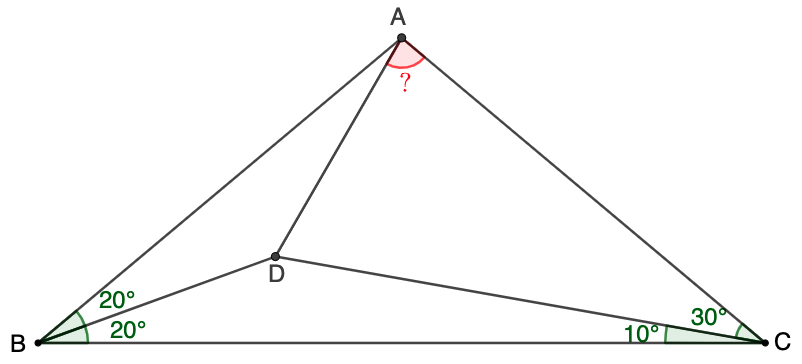
Solve:
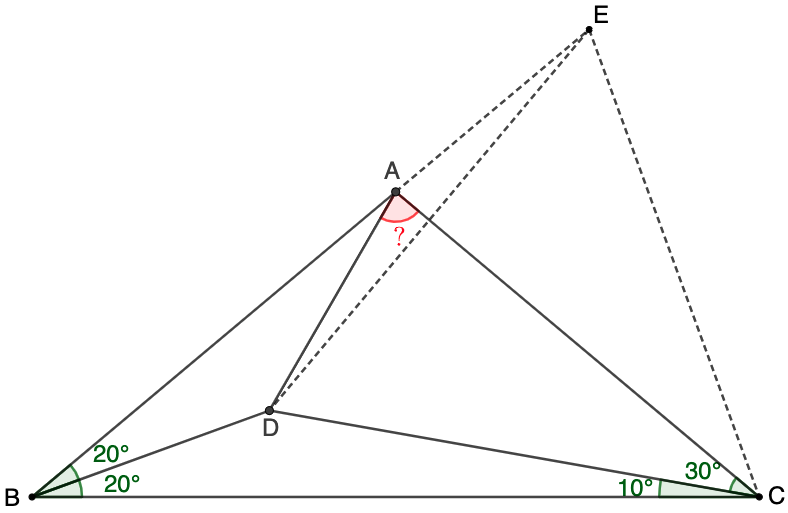\(\begin{multline}\nonumber
\shoveleft \text{Extend } BA \text{ to } E \text{ such that } BC=BE\\
\shoveleft \angle{EBD}=\angle{CBD} \implies \triangle{DBE} \cong \triangle{CBD} \\
\shoveleft \implies \angle{BED}=\angle{BCD}=10^{\circ}, CD=DE, \angle{CDE}=2(20^{\circ}+10^{\circ})=60^{\circ}\\
\shoveleft \implies \triangle{CDE} \text{ is equilateral} \implies CE=CD=DE, \angle{DCE}=60^{\circ}\\
\shoveleft \implies \angle{ACE}=30^{\circ}=\angle{ACD} \implies \triangle{ACD} \cong \triangle{ACE} \\
\shoveleft \implies AD=AE, \angle{CAD}=\angle{CAE} \implies \angle{ADE}=\angle{AED}=10^{\circ}\\
\shoveleft \implies \angle{CAD} = \dfrac{180^{\circ}-2*10^{\circ}}{2}=\bbox[5px, border: 1px solid black]{80^{\circ}}
\end{multline}\)
02/15/2023
$D$ is a point inside equilateral triangle $\triangle{ABC}$ such that $\angle{BCD}=54^{\circ}, \angle{CBD}=42^{\circ}$, find $\angle{BAD}$
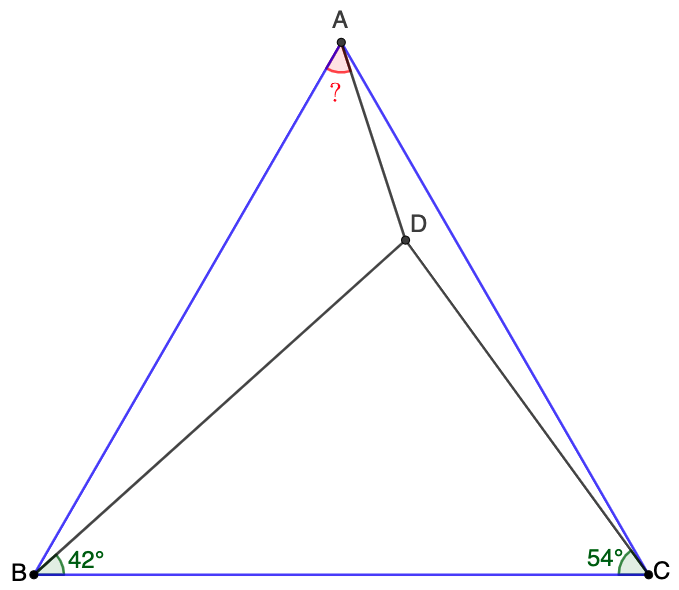
Solve 1:
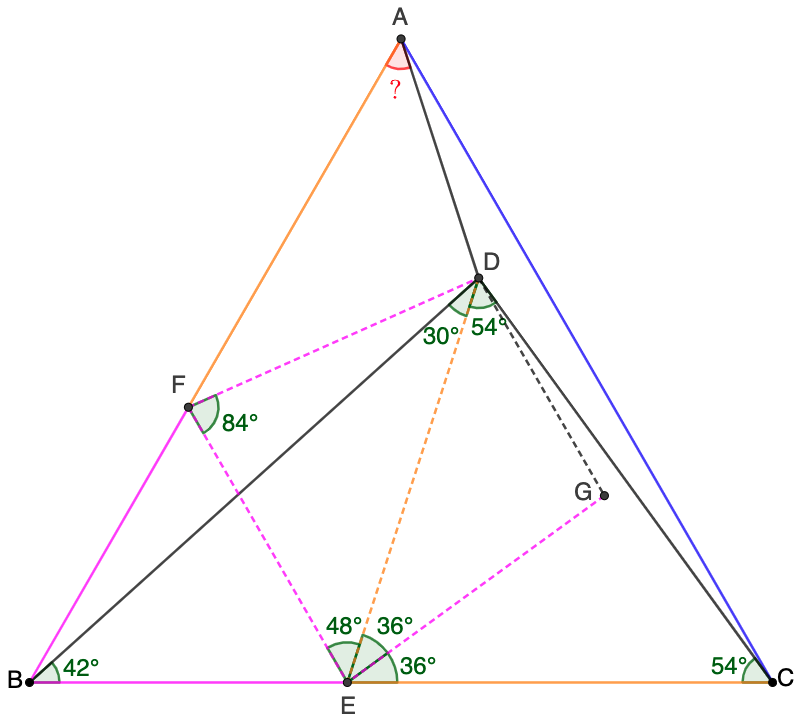\(\begin{multline}\nonumber
\shoveleft \text{Make } E \text{ on } BC \text{ such that } \angle{CDE}=54^{\circ}=\angle{DCE}\\
\shoveleft \text{Make } F \text{ on } AB \text{ such that } EF \parallel AC, \triangle{BEF} \text{ is equilateral}\\
\shoveleft \text{Make } EG \text{ bisects } \angle{CED} \text{ and } EF=EG, \text{ easy to see that }\\
\shoveleft \angle{CEG}=\angle{DEG}=36^{\circ}, \angle{DEF}=180^{\circ}-60^{\circ}-72^{\circ}=48^{\circ}\\
\shoveleft \implies \angle{BDE}=180^{\circ}-42^{\circ}-2*54^{\circ}=30^{\circ}, BF=EF, \angle{BFE}=2\angle{BDE}\\
\shoveleft \implies F \text{ is circumcenter of } \triangle{BDE} \implies BF=EF=DF=BE=EG \\
\shoveleft \implies \angle{EDF}=\angle{DEF}=48^{\circ}, \angle{FBD}=\angle{FDB}=18^{\circ} \implies \angle{AFD}=36^{\circ}\\
\shoveleft \implies AF=CE=DE, DF=EG, \angle{AFD}=\angle{DEG} \implies \triangle{AFD} \cong \triangle{DEG}\\
\shoveleft \angle{EFD}=84^{\circ}=\angle{FEG} \implies {DFEG} \text{ is isosceles trapezoid }\\
\shoveleft \implies \angle{BAD}=\angle{EDG}=\angle{FED}=\bbox[5px, border: 1px solid black]{48^{\circ}}\\
\end{multline}\)
02/20/2023
Two parallelograms $ABCD$ and $AECF$ share the same diagonal $AC$. $E$ and $F$ are inside $ABCD$. Prove that there is the circumcircles of $\triangle{AEB}, \triangle{BFC}, \triangle{CED}$ and $\triangle{DFA}$ share a same intersection point (from Germany Competition)
Prove:
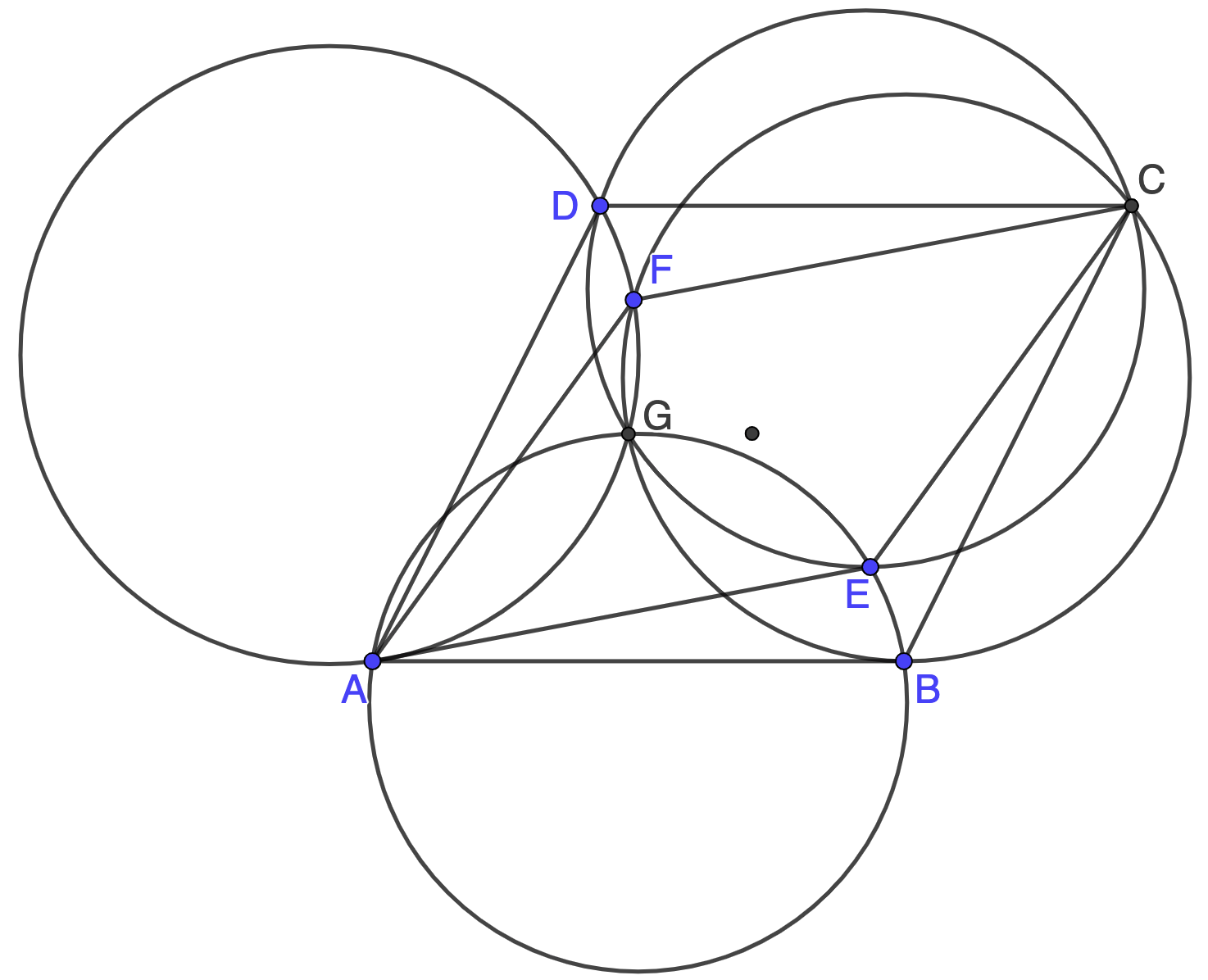
Prove:
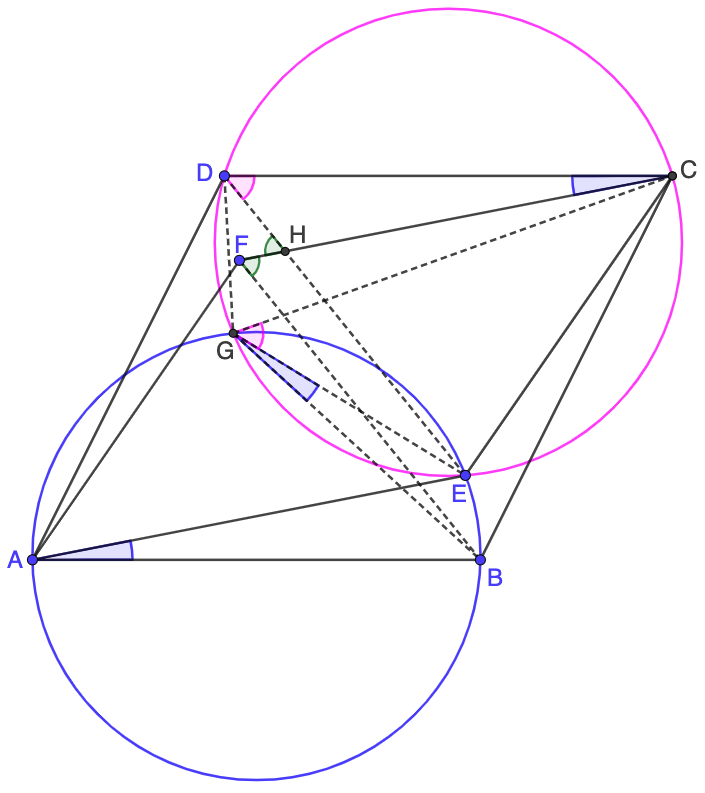\(\begin{multline}\nonumber
\shoveleft \angle{CAB}=\angle{ACD}, \angle{CAE}=\angle{ACF} \implies \angle{EAB}=\angle{FCD}\\
\shoveleft \implies \angle{FAB}=\angle{ECD} \implies \triangle{ABF} \cong \triangle{CDE} \implies \angle{AFB}=\angle{CED}\\
\shoveleft AECF \text{ is parallelogram } \implies \angle{AFE}=\angle{EFC} \implies \angle{BFE}=\angle{EFB} \implies BF \parallel DE\\
\shoveleft \text{ Let } H \text{ be intersection of } CF \text{ and } DE \implies \angle{BFC}=\angle{DHF}\\
\shoveleft ABEG \text{ is cyclic} \implies \angle{EAB}=\angle{BGE}=\angle{DCF}, CDGE \text{ is cyclic} \implies \angle{EGC}=\angle{EDC}\\
\shoveleft \angle{BGE}+\angle{EGC}=\angle{BGC}=\angle{EDC}+\angle{DCF}=\angle{DHF}=\angle{BFC} \implies BCFG \text{ is cyclic}\\
\shoveleft \implies G \text{ is on circumcircle of } \triangle{BFC}. \text{Similially, } ADFG \text{ is cyclic and } G \text{ is on circumcicle of } \triangle{DFA}\\
\shoveleft \implies \text{The circumcircles of } \triangle{AEB}, \triangle{BFC}, \triangle{CED} \text{ and } \triangle{DFA} \text{ share a same intersection point: } G \quad \blacksquare \\
\end{multline}\)
02/23/2023
(1) How many different ways to arrange 4 couples in a row such that no one sits next to his/her spouse? (2) How many ways to arrange 4 couples around a round table such that no one sits next to his/her spouse?
Solve:
(1) \(\begin{multline}\nonumber \shoveleft \text{Applying PIE (Principle of Inclusion and Exclusion):}\\ \shoveleft \text{ANS } = \text{ Total permutations - at least 1 couple is adjacent to each other} \\ \shoveleft + \text{ at least 2 couples are adjacent to each other} \\ \shoveleft - \text{ at least 3 couples are adjacent to each other} \\ \shoveleft + \text{ 4 couples are adjacent to each other}\\ \shoveleft = 8! - {4 \choose 1} \cdot 2 \cdot 7! + {4 \choose 2} \cdot 2^2 \cdot 6! - {4 \choose 3} \cdot 2^3 \cdot 5! + 2^4 \cdot 4! = \bbox[5px, border: 1px solid black]{13824}\\ \end{multline}\)
(2) \(\begin{multline}\nonumber \shoveleft \text{We know the circular permutations for } n \text{ distinct elements are } (n-1)! \\ \shoveleft \text{Applying PIE (Principle of Inclusion and Exclusion):}\\ \shoveleft \text{ANS } = \text{ Total circular permutations - circular permutations at least 1 couple is adjacent to each other} \\ \shoveleft + \text{ circular permutations at least 2 couples are adjacent to each other} \\ \shoveleft - \text{ circular permutations at least 3 couples are adjacent to each other} \\ \shoveleft + \text{ circular permutations that 4 couples are adjacent to each other}\\ \shoveleft = 7! - {4 \choose 1} \cdot 2 \cdot 6! + {4 \choose 2} \cdot 2^2 \cdot 5! - {4 \choose 3} \cdot 2^3 \cdot 4! + 2^4 \cdot 3! = \bbox[5px, border: 1px solid black]{1488}\\ \end{multline}\)
Reference:
02/24/2023
In quarter circle centered at $O$, $C$ is a point on arc $\overset{\huge\frown}{AB}$, and $AC=10\sqrt{2}, BC=6$. Find the area of $AOBC$
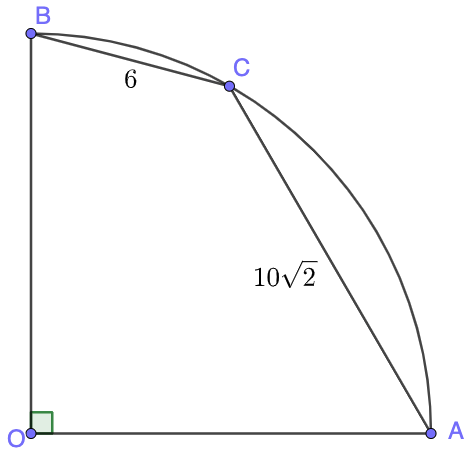
Solve:
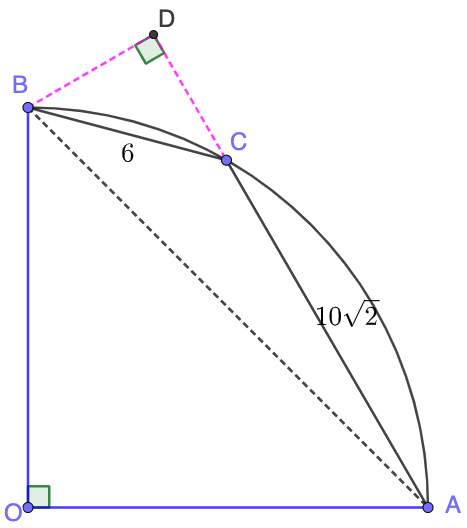\(\begin{multline}\nonumber
\shoveleft \text{Connect } AB \text{ and extend } AC \text{ to } D \text{ such that }BD \perp AD\\
\shoveleft \angle{BCD}=\angle{ABC}+\angle{BAC}=\dfrac{AOC}{2} + \dfrac{BOC}{2}=\dfrac{90^{\circ}}{2}=45^{\circ}\\
\shoveleft \implies BD=CD=\dfrac{BC}{\sqrt{2}}=3\sqrt{2} \implies AD=13\sqrt{2}\\
\shoveleft \implies AB=\sqrt{2} AO=\sqrt{2} BO=\sqrt{18+338}=\sqrt{356}\\
\shoveleft [AOBC]=[AOB]+[ABC]=\dfrac{AB^2}{4}+\dfrac{AC \cdot BD}{2}\\
\shoveleft \implies [AOBC] = 89 + 30 = \bbox[5px, border: 1px solid black]{119}
\end{multline}\)