M∀TH Workout

January 2023

 
  • Jan 14, 2023

01/14/2023

$\triangle{ABC}$ has $\angle{ABC}=50^{\circ}$, $D$ is a point in $\triangle{ABC}$ such that $\angle{ABD}=10^{\circ}, \angle{DAB}=20^{\circ}, \angle{DCB}=30^{\circ}$, find $\angle{ACD}$.

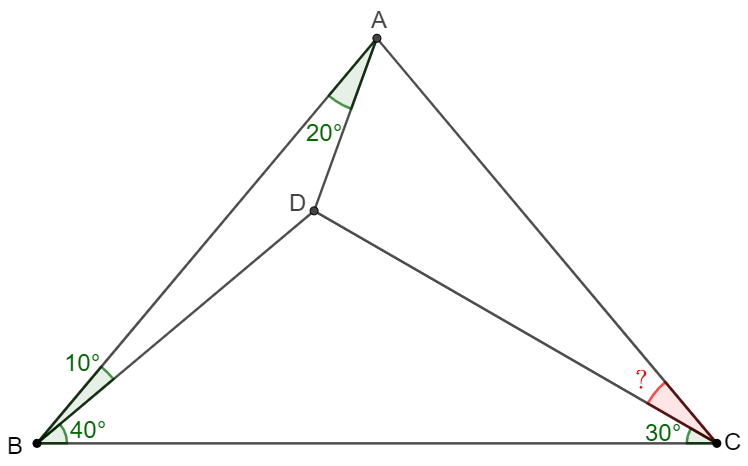
image-20230114161720898

Solve 1:

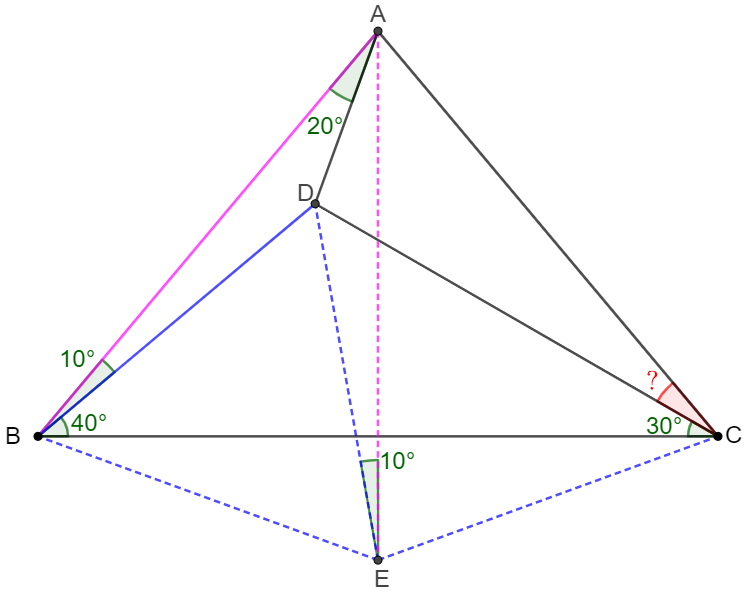image-20230114163420593 \(\begin{multline}\nonumber \shoveleft \text{Make } E \text{ be circumcenter of } \triangle{BCD}, \text{ connect } AE, BE, CE, DE\\ \shoveleft \angle{BCD}=30^{\circ}, \angle{CBD}=40^{\circ }\implies \triangle{BDE} \text{ is equilateral}, \angle{CED}=80^{\circ}\\ \shoveleft \implies BD=DE=BE=CE, \angle{BDE}=\angle{DBE}=\angle{BED}=60^{\circ}\\ \shoveleft \implies \angle{ADE}=360^{\circ}-\angle{ADB}-60^{\circ}=150^{\circ}=\angle{ADB}\\ \shoveleft \triangle{ADB} \cong \triangle{ADE} \implies \angle{AED}=\angle{ABD}=10^{\circ}\\ \shoveleft \implies \angle{AEB}=10^{\circ}+60^{\circ}=70^{\circ}=\angle{CED}-\angle{AED}\\ \shoveleft \implies \triangle{AEB} \cong \triangle{AEC} \implies AB=AC\\ \shoveleft\implies \angle{ACD}=50^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}} \end{multline}\) Solve 2:

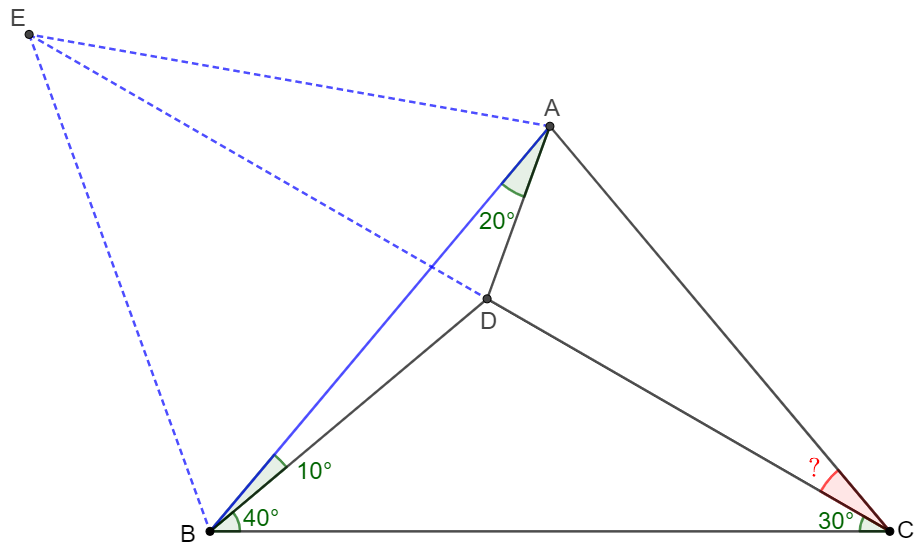image-20230114164042713 \(\begin{multline}\nonumber \shoveleft \text{Make } E \text{ be circumcenter of } \triangle{ABD}, \text{ connect } AE, BE, DE\\ \shoveleft \angle{ABD}=10^{\circ}, \angle{BAD}=20^{\circ }\implies \angle{AED}=20^{\circ}, \angle{BED}=40^{\circ}, AE=BE=DE\\ \shoveleft \implies \angle{DBE}=\angle{BDE}=70^{\circ}=180^{\circ}-\angle{BDC} \implies \angle{ABE}=60^{\circ}\\ \shoveleft \implies \triangle{ABE} \text{ is equilateral, C, D, E are collinear} \\ \shoveleft \implies \angle{BAE}=60^{\circ}=2\angle{BCE}, AE=BE \implies A \text{ is circumcenter of } \triangle{BCE}\\ \shoveleft \implies AB=AC \implies \angle{ACD}=50^{\circ}-30^{\circ}=\bbox[5px, border: 1px solid black]{20^{\circ}} \end{multline}\)

01/30/2023

Point $E$ on side $AC$ of rectangle $ABCD$ such that $AE=2, CE=4, \angle{BED}=120^{\circ}$, find $AB$.

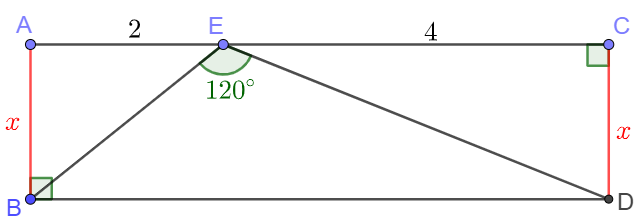
image-20230130194139978

Solve 1:

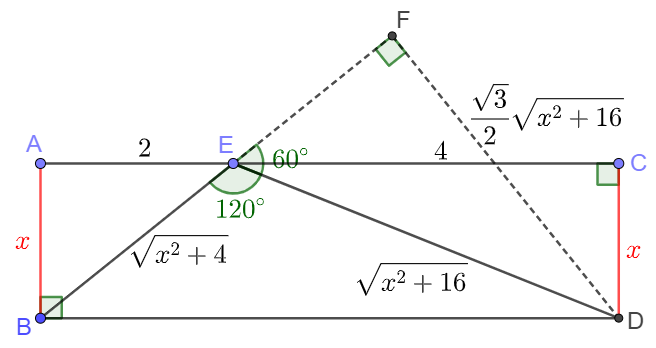image-20230130194545628 \(\begin{multline}\nonumber \shoveleft \text{Extend } BE \text{ and let } DF \perp BE \text{ at } F. \\ \shoveleft BE=\sqrt{x^2+4}, DE=\sqrt{x^2+16}, \angle{DEF}=60^{\circ} \\ \shoveleft DF=\dfrac{\sqrt{3}}{2}DE=\dfrac{\sqrt{3}}{2}\sqrt{x^2+16} \\ \shoveleft [BDE]=[ABE]+[CDE] \implies 3x=\dfrac{BE \cdot DF}{2} \\ \shoveleft \implies 3x=\dfrac{\sqrt{3}}{4}\sqrt{x^2+4}\sqrt{x^2+16} \\ \shoveleft \implies 48x^2=(x^2+4)(x^2+16) \\ \shoveleft \implies x^4-28x^2+144=0 \implies x^2=14-2\sqrt{33} \\ \shoveleft \implies x=\bbox[5px, border: 1px solid black]{\sqrt{11}-\sqrt{3}} \end{multline}\)

Solve 2:

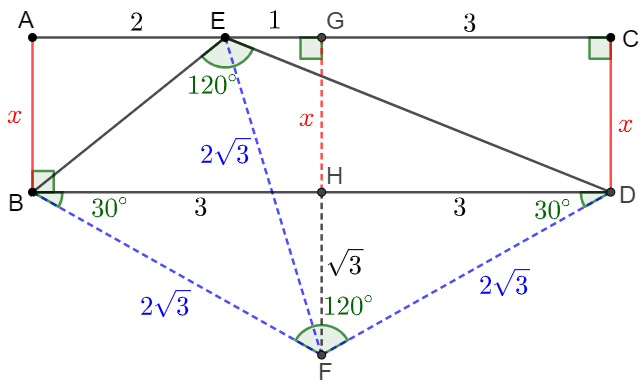image-20230130232518473 \(\begin{multline}\nonumber \shoveleft \text{Let } F \text{ be the circumcenter of } \triangle{BDE}, \text{ make } FG \perp AC, FG \text{ and } BD \text{ intersects at } H.\\ \shoveleft \implies BF=DF=EF, \angle{BFD}=2*(180^{\circ}-\angle{BED})=120^{\circ} \\ \shoveleft \implies \angle{FBD}=\angle{FDB}=30^{\circ}, BD=6, BH=HD=AG=3, BF=EF=DF=2\sqrt{3}, HF=\sqrt{3}\\ \shoveleft \implies EG=AG-AE=1 \implies FG=\sqrt{EF^2-EG^2}=\sqrt{11} \implies GH=x=\bbox[5px, border: 1px solid black]{\sqrt{11}-\sqrt{3}} \end{multline}\)

01/21/2023

$E$ is on side $AD$ of rectangle $ABCD$ such that $AE=3, DE=6, \angle{BEC}=60^{\circ}$, find $[BCE]$

Solve:

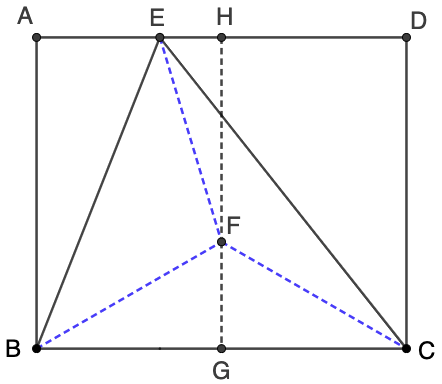image-20230215005317987 \(\begin{multline}\nonumber \shoveleft \text{Let } F \text{ be the circumcenter of } \triangle{BCE}, \text{ easy to see that }\\ \shoveleft BF=CF=EF, \angle{BFC}=2\angle{BEC}=2*60^{\circ}=120^{\circ}\\ \shoveleft \text{ Make perpendicular line of } BC \text{ and } AD \text{ through } F \text{ at } G, H,\\ \shoveleft \text{ easy to see } \triangle{BFG} \cong \triangle{CFG}\\ \shoveleft \implies \angle{BFG}=\angle{CFG}=\dfrac{\angle{BFC}}{2}=60^{\circ}, \\ \shoveleft BG=CG=AH=DH=\dfrac{AE+DE}{2}=\dfrac{9}{2},\\ \shoveleft EH=AH-AE=\dfrac{9}{2}-3=\dfrac{3}{2}\\ \shoveleft \implies FG=\dfrac{BG}{\sqrt{3}}=\dfrac{9}{2\sqrt{3}}, BF=EF=CF=2FG=\dfrac{9}{\sqrt{3}},\\ \shoveleft FH=\sqrt{EF^2-EH^2}=\sqrt{\dfrac{81}{3}-\dfrac{9}{4}}=\sqrt{\dfrac{99}{4}}=\dfrac{3}{2}\sqrt{11}\\ \shoveleft \implies GH=FG+FH=\dfrac{9}{2\sqrt{3}}+\dfrac{3}{2}\sqrt{11}=\dfrac{3}{2}(\sqrt{11} + \sqrt{3})\\ \shoveleft \implies S_{\triangle{BCE}}=\dfrac{1}{2} \cdot 9 \cdot\dfrac{3}{2}(\sqrt{11} + \sqrt{3})=\bbox[5px, border: 1px solid black]{\dfrac{27}{4}(\sqrt{11}+\sqrt{3})} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search