12/18/2022

In rectangle $ABCD$, $E, F$ are points on side $BC, CD$ respectively. $[ABE]=a, [ADF]=b, [CEF]=c$, find $S=[AEF]$.

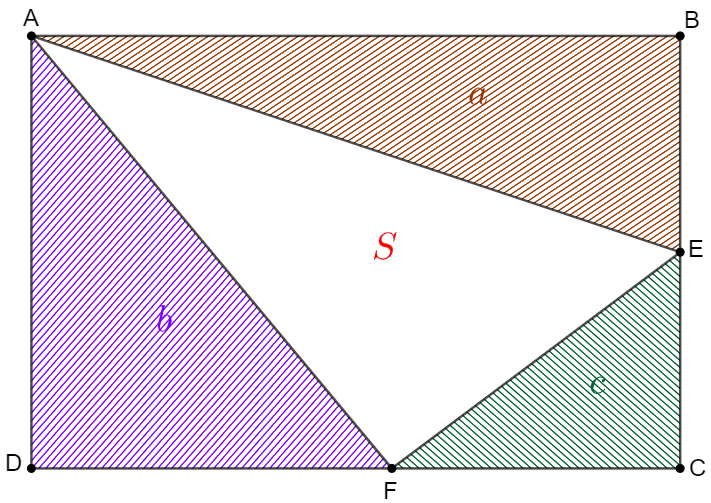
Solve:

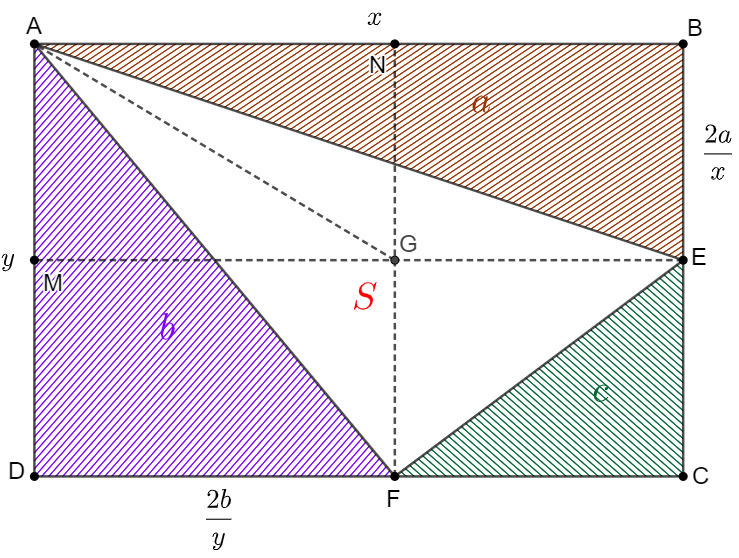
\(\begin{multline}\nonumber \shoveleft \text{Make }EM, FN \text{ parallel to the side of the rectangle } ABCD, \text{ and they intersect at } G\\ \shoveleft \text{Suppose }AB=x, AD=y, [ABE]=a \implies BE=\cfrac{2a}{x}, [ADF]=b\implies DF=\cfrac{2b}{y}\\ \shoveleft \implies S=[AEF]=[AGE]+[AGF]+[EFG]=[AME]-[AMG]+[ANF]-[ANG]+[CEF],\\ \shoveleft [AME]=a, [ANF]=b, [EFG]=c, [AMG]=[ANG]=\cfrac{DF \cdot BE}{2}=\cfrac{2ab}{xy}, xy=S+a+b+c\\ \shoveleft \implies S=[AEF]=a+b+c-\cfrac{4ab}{xy}=a+b+c-\cfrac{4ab}{S+a+b+c}\\ \shoveleft \implies (a+b+c)-S=\cfrac{4ab}{(a+b+c)+S} \implies {S^2=(a+b+c)^2-4ab}\\ \shoveleft \implies S=\bbox[5px, border: 1px solid black]{\sqrt{(a+b+c)^2-4ab}}\\ \end{multline}\)

---