M∀TH Workout

November 2022

 
  • Nov 05, 2022

11/09/2022

Find the area of the shaded region:

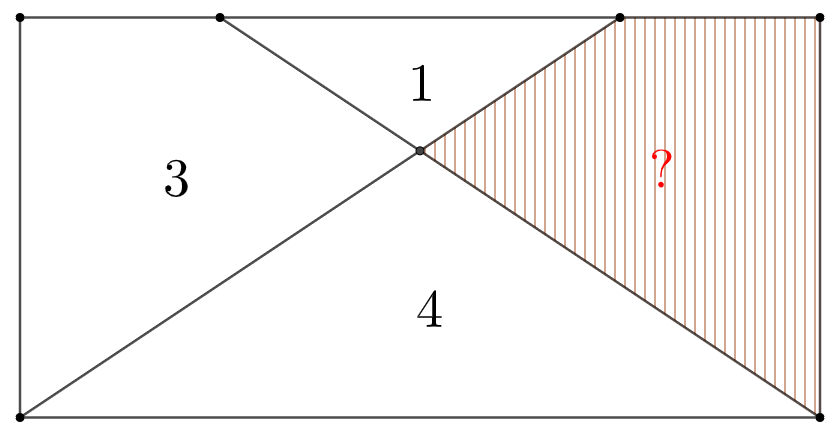
image-20221109183404620

Solve:

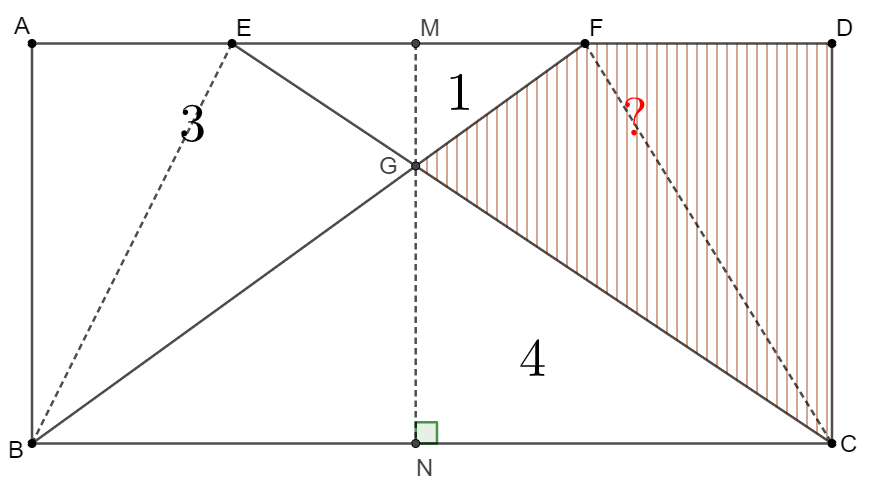image-20221111041210765 \(\begin{multline}\nonumber \shoveleft \text{Make } MN\perp BC \text{ ,and the perpendicular feet are } M \text{ and } N, \text{easy to see}\\ \shoveleft \triangle{BCG} \sim \triangle{EFG} \implies \cfrac{EF}{BC}=\cfrac{MG}{NG} \implies \cfrac{[EFG]}{[BCG]}=\Bigl(\cfrac{EF}{BC}\Bigr)^2=\Bigl( \cfrac{EG}{GC} \Bigr)^2=\Bigl( \cfrac{FG}{GB} \Bigr)^2=4\\ \shoveleft \implies \cfrac{EF}{BC}=\cfrac{EG}{GC}=\cfrac{FG}{GB}=\cfrac{1}{2} \implies \cfrac{[EBG]}{[EFG]}=\cfrac{[FCG]}{[FEG]}=2 \implies [EBG]=[FCG]=2\\ \shoveleft \implies [AEB]=3-[EBG]=1 \implies \cfrac{AE}{EF}=\cfrac{1}{3} \implies AE= \cfrac{1}{3}\cdot \cfrac{1}{2} BC=\cfrac{1}{6}BC\\ \shoveleft \implies DF=\Bigl(1-\cfrac{1}{6}-\cfrac{1}{2}\Bigr)BC=\cfrac{1}{3}BC \implies \cfrac{[CFD]}{[CEF]}=\cfrac{DF}{EF}=\cfrac{2}{3} \implies [CFD]=\cfrac{2}{3}\cdot 3=2 \\ \shoveleft \implies [CDFG]=[CDF]+[CFG]=2+2=\bbox[5px, border: 1px solid black]{4}\\ \end{multline}\)

11/12/2022

In $\triangle{ABC}$, $\angle{ABC}=40^{\circ}, $D$ is a point on side $BC$ such that $\angle{BAD}=60^{\circ}, CD=AB$. Find $\angle{ACB}$.

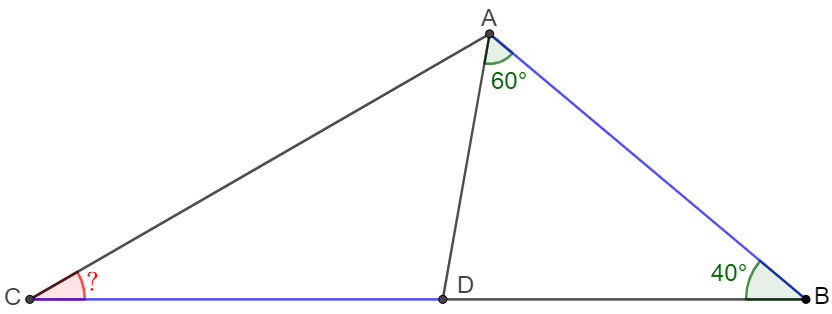
image-20221111233832752

Solve:

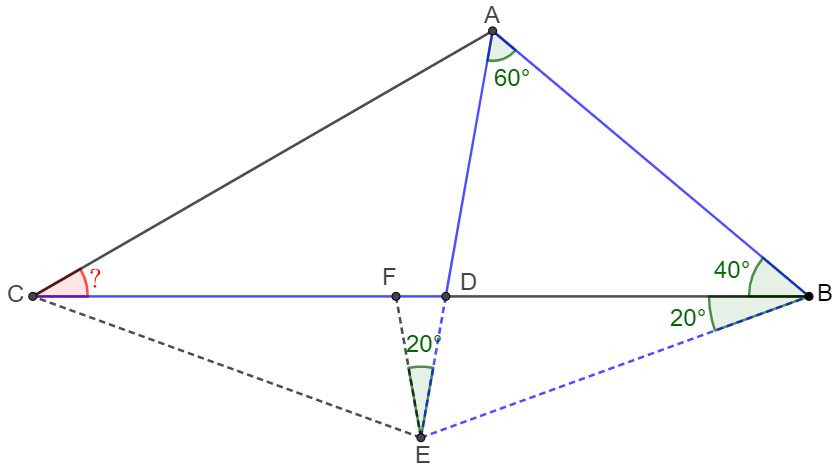
image-20221111234116180

. \(\begin{multline}\nonumber \shoveleft \text{Build equilateral triangle } \triangle{ABE} \text{ such that } E \text{ is the third vertex of it. Connect CE.}\\ \shoveleft \implies \angle{DBE}=20^{\circ}, AB=AE=BE, \angle{BED}=60^{\circ}\\ \shoveleft \text{Make } F \text{ on } BC \text{ such that } BE=BF \implies \angle{BFE}=\angle{FEB}=80^{\circ}\\ \shoveleft \implies \angle{DEF}=20^{\circ} \implies \angle{EDF}=80^{\circ}=\angle{BFE} \implies DE=EF\\ \shoveleft CD=AB=BE=BF \implies CF=DB \implies \triangle{CEF} \cong \triangle{BED} \implies BE=CE=AE\\ \shoveleft \implies E \text{ is circumcenter of } \triangle{ABC} \implies \angle{ACB}=\cfrac{\angle{AEB}}{2}=\bbox[5px, border: 1px solid black]{30^{\circ}}\\ \end{multline}\)

11/13/2022

In $\triangle{ABC}, B>AC$. $E$ is a point on bisector of $\angle{BAC}$. Prove that $BE>CE$.

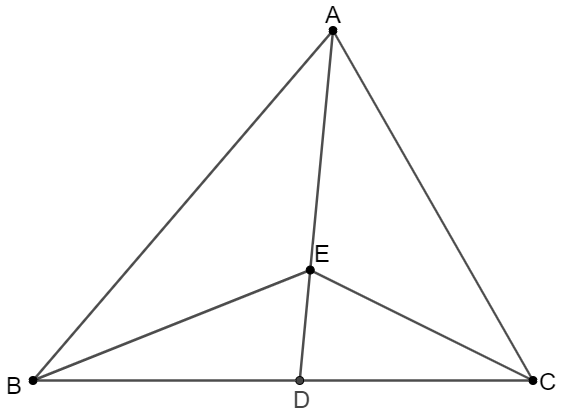
image-20221112144350448

Prove:

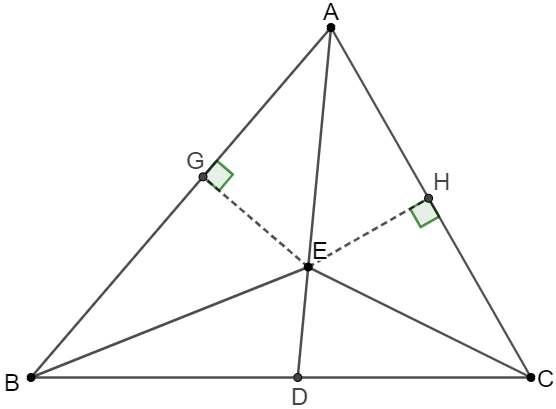image-20221112144621796 \(\begin{multline}\nonumber \shoveleft \text{Make } G, H \text{ on } AB, AC \text{ respectively such that } EG \perp AB, EH \perp AC.\\ \shoveleft AE \text{ bisects } \angle{BAC} \implies AG=AH, EG=EH\\ \shoveleft AB>AC \implies AB-AG>AC-AH \implies BG>CH\\ \shoveleft \implies BE^2=BG^2+EG^2=BG^2+EH^2>CH^2+EH^2=CE^2\\ \shoveleft \implies BE>CE \qquad \blacksquare \end{multline}\)

11/14/2022

In $\triangle{ABC}, AB=AC=10, BC=12$. Point $D$ lies strictly between $A$ and $B$ on $\overline{AB}$ and point $E$ lies strictly between $A$ and $C$ on $\overline{AC}$ so that $AD=DE=EC$. Then $AD$ can be expressed in the form $\cfrac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p-6q$.

Solve: \(\begin{multline}\nonumber \shoveleft sin\Bigl(\cfrac{A}{2}\Bigr)=\cfrac{3}{5}, cos\Bigl(\cfrac{A}{2} \Bigr)=\cfrac{4}{5} \implies cosA=2\cdot\Bigl(\cfrac{4}{5} \Bigr)^2-1=\cfrac{7}{25}\\ \shoveleft cosA=\cfrac{\cfrac{AE}{2}}{AD}=\cfrac{\cfrac{AC-CE}{2}}{AD}=\cfrac{\cfrac{10-AD}{2}}{AD}=\cfrac{10-AD}{2AD}=\cfrac{7}{25}\\ \shoveleft \implies AD=\cfrac{250}{39} \implies p=250, q=39 \implies p-6q = \bbox[5px, border: 1px solid black]{16} \end{multline}\)

11/15/2022

There are 8 horses in a horse race. Times are rounded to the nearest second, so it is very possible for horses to tie. How many different ways can the horses place in the race? For example, one placement would have all of them tied. Another 8! different placements would have none of them tied.

Solve:

This number is an ordered Bell number when $n=8$: \(\begin{multline} \nonumber \shoveleft a(0)=1, a(n)=\displaystyle \sum_{k=1}^{n}{ {n \choose k} \cdot a(n-k) }\\ \shoveleft a(1)={1 \choose 1} a(1-1) = 1\\ \shoveleft a(2)={2 \choose 1} a(2-1) = 3\\ \shoveleft a(3)={3 \choose 1} a(3-1) + {3 \choose 2} a(3-2) + {3 \choose 3} a(3-3)=13\\ \shoveleft a(4)={4 \choose 1} a(4-1) + {4 \choose 2} a(4-2) + {4 \choose 3} a(4-3) + {4 \choose 4} a(4-4)=75\\ \shoveleft a(5)={5 \choose 1} a(5-1) + {5 \choose 2} a(5-2) + {5 \choose 3} a(5-3) + {5 \choose 4} a(5-4) + {5 \choose 5} a(5-5) =541\\ \shoveleft a(6)={6 \choose 1} a(6-1) + {6 \choose 2} a(6-2) + {6 \choose 3} a(6-3) + {6 \choose 4} a(6-4) + {6 \choose 5} a(6-5) + {6 \choose 6} a(6-6)=4683\\ \shoveleft a(7)={7 \choose 1} a(7-1) + {7 \choose 2} a(7-2) + {7 \choose 3} a(7-3) + {7 \choose 4} a(7-4) + {7 \choose 5} a(7-5) + {7 \choose 6} a(7-6) + {7 \choose 7}a(7-7)=47293\\ \shoveleft a(8)={8 \choose 1} a(8-1) + {8 \choose 2} a(8-2) + {8 \choose 3} a(8-3) + {8 \choose 4} a(8-4) + {8 \choose 5} a(8-5) + {8 \choose 6} a(8-6) + {8 \choose 7}a(8-7) + {8 \choose 8}a(8-8)=\bbox[5px, border: 1px solid black]{545835}\\ \end{multline}\)

References:

11/16/2022

In square $ABCD$, $\angle{CBE}=\angle{EBF}, CE=39, AF=25$, find $BF$.

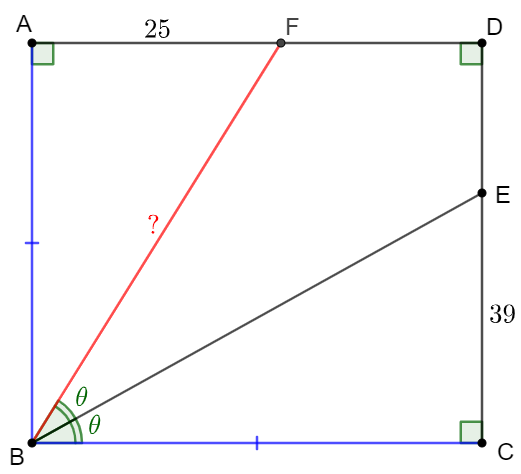
image-20221114003626089

Solve:

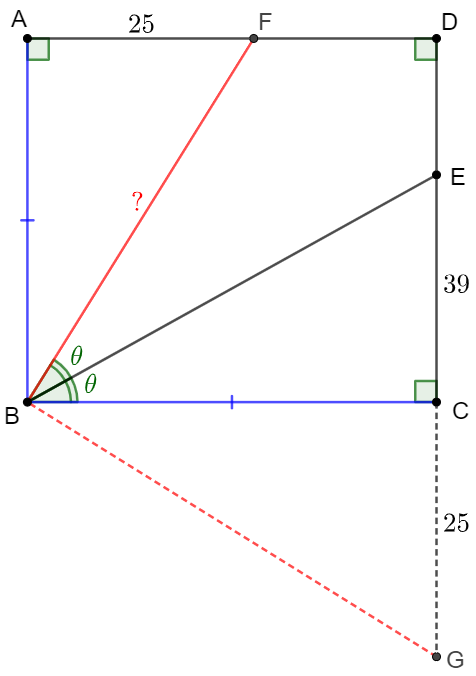image-20221114003700716 \(\begin{multline}\nonumber \shoveleft \text{Extend }DC \text{ to } G \text{ such that }CD=AF=25\\ \shoveleft \text{Easy to see that } \triangle{ABF} \cong \triangle{CBG}\\ \shoveleft \implies BF=BG, \angle{ABF}=\angle{CBG} \implies \angle{BEG}=\angle{EBA}=\angle{EBG}\\ \shoveleft \implies BF=BG=EG=39+25=\bbox[5px, border: 1px solid black]{64} \end{multline}\)

11/17/2022

In a tetrahedron $ABCD$, $E, F$ are points on $BC, AD$, respectively. $AB=4, CD=20, EF=7, \cfrac{AF}{FD}=\cfrac{BE}{EC}=\cfrac{1}{3}$. Find the angle between $AB$ and $CD$.

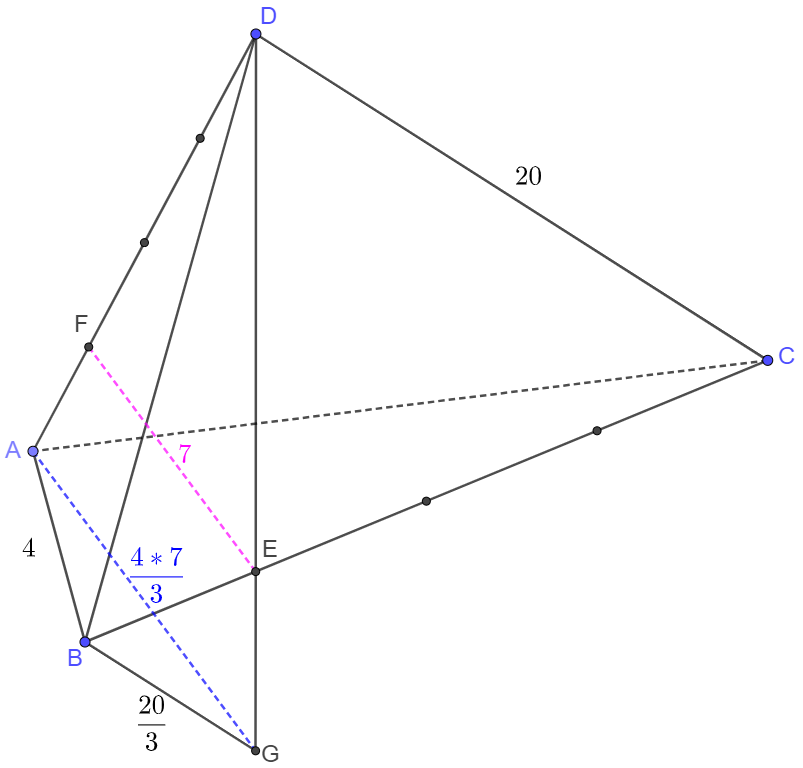
image-20221114025242803

Solve: \(\begin{multline}\nonumber \shoveleft \text{Make } G \text{ on extended} DE \text{ such that } BG \parallel CD, \text{ conect }AG\\ \shoveleft \implies \triangle{BEG} \sim \triangle{CED} \implies \cfrac{GE}{DE}=\cfrac{BG}{CD}=\cfrac{BE}{CE}=\cfrac{1}{3} \implies BG=\cfrac{20}{3}\\ \shoveleft \implies \cfrac{AF}{FD}=\cfrac{GE}{ED} \implies \triangle{DEF} \sim \triangle{DAG} \implies \cfrac{AG}{FE}=\cfrac{AD}{FD}=\cfrac{4}{3} \implies AG=7 \cdot \cfrac{4}{3}\\ \shoveleft \implies cos(\angle{ABG})=\cfrac{4^2+\Bigl(\cfrac{20}{3}\Bigl)^2-\Bigl(\cfrac{28}{3}\Bigl)^2}{2*4*\cfrac{20}{3}}=-\cfrac{1}{2} \implies \angle{ABG}=\bbox[5px, border: 1px solid black]{120^{\circ}} \end{multline}\)

Note:

  • For $\triangle{ABC}, AB:BC:CA=3:5:7 \implies \angle{ABC}=120^{\circ}$, the angle facing side $7$ is $120^{\circ}$.
  • For $\triangle{ABC}, AB:BC:CA=5:7:8 \implies \angle{BAC}=60^{\circ}$, the angle facing side $7$ is $60^{\circ}$.

11/18/2022

$D$ is a point on side $BC$ of $\triangle{ABC}$. $\angle{ACB}=80^{\circ}, \angle{ADC}=70^{\circ}, AB=AC+CD.$ Find $\angle{ABC}$.

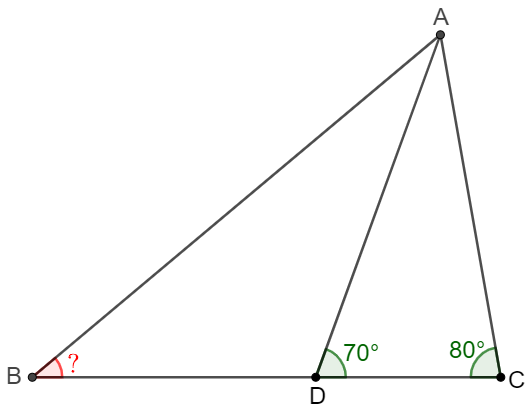
image-20221117045510089

Solve:

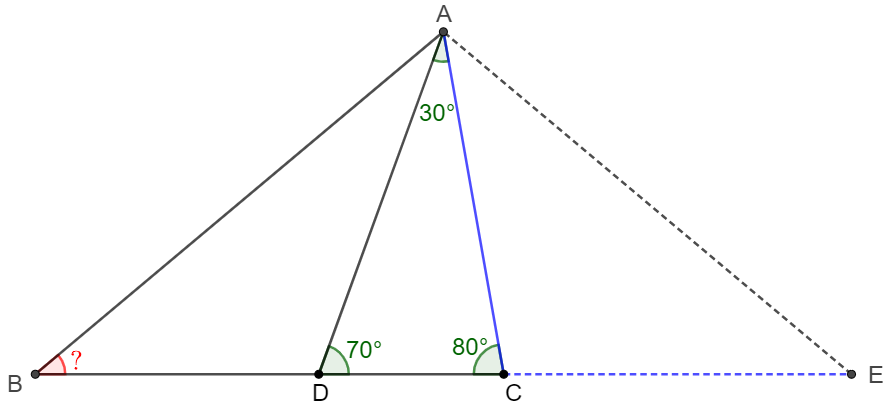image-20221117045411654 \(\begin{multline}\nonumber \shoveleft \text{Easy to see that } \angle{CAD}=30^{\circ}. \text{ Extend } BC \text{ to } E \text{ such that } AC=AE\\ \shoveleft \implies \angle{CAE}=\angle{AEC}=40^{\circ} \implies \angle{DAE}=30^{\circ}+40^{\circ}=\angle{ADC}\\ \shoveleft \implies AE=DE=AC+CD=AB \implies \angle{ABC}=\angle{AEC}=\bbox[5px, border: 1px solid black]{40^{\circ}} \end{multline}\)

Note:

This problem can be generalized to:

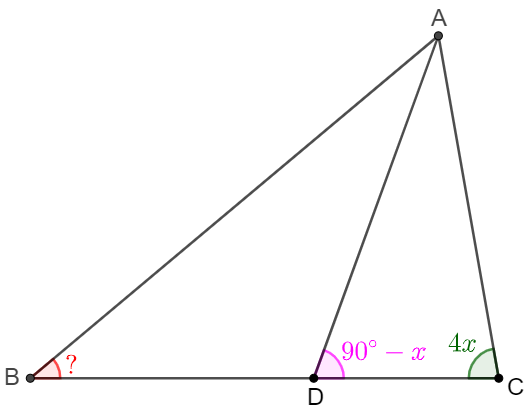
image-20221117050451160

image-20221117050818624

11/19/2022

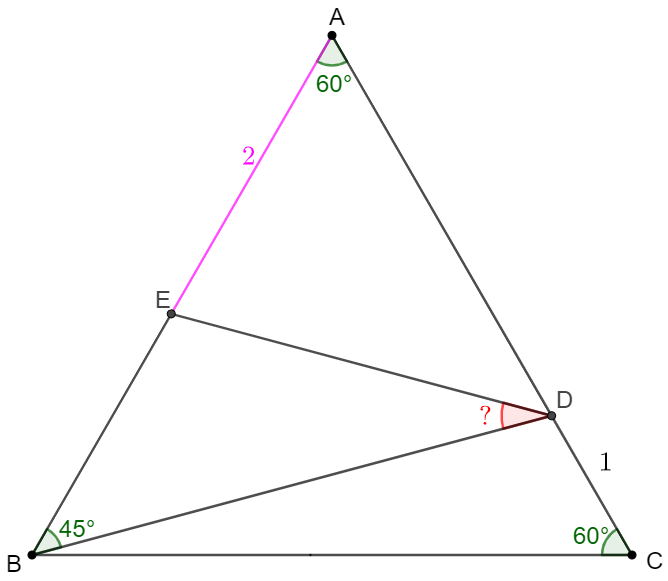
In equilateral triangle $\triangle{ABC}$, $D$ and $E$ are on side $AC$ and $AB$ respectively, and $CD=1, AE=2, \angle{DBE}=45^{\circ}$. Find $\angle{BDE}$.

image-20221117165706619

Solve:

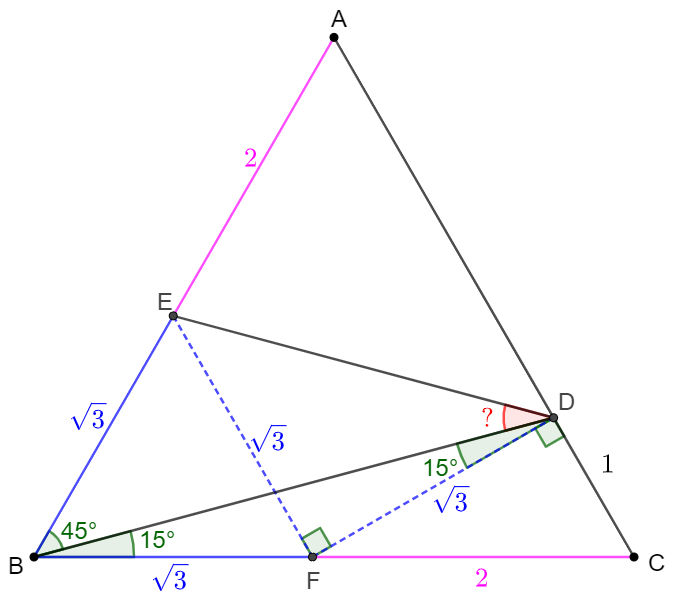image-20221117165454450 \(\begin{multline}\nonumber \shoveleft \text{Make } F \text{ on side } BC \text{ such that } CF=AE=2\\ \shoveleft \implies EF \parallel AC, FD\perp AC, \angle{CFD}=30^{\circ}\\ \shoveleft \implies \triangle{BEF} \text{ is equilateral} \implies BF=EF, \angle{BFE}=60^{\circ} \\ \shoveleft \implies \angle{BDF}=30^{\circ}-\angle{DBC}=30^{\circ}-15^{\circ}=15^{\circ}=\angle{DBC} \\ \shoveleft \implies BF=EF=DF, \angle{EFD}=180^{\circ}-60^{\circ}-30^{\circ}=90^{\circ}\\ \shoveleft \implies \angle{EDF}=45^{\circ} \implies \angle{BDE}=45^{\circ}-15^{\circ}=\bbox[5px, border: 1px solid black]{30^{\circ}} \end{multline}\)

11/20/2022

Solve the angle:

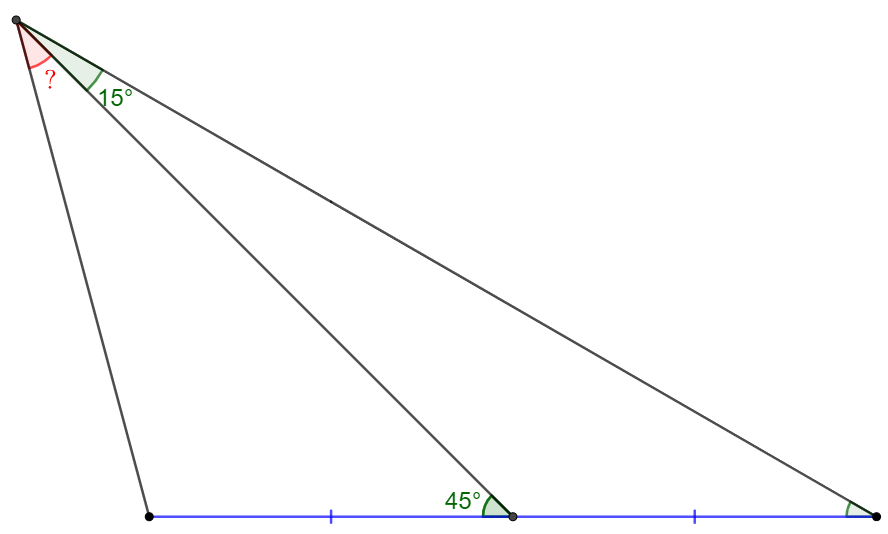
image-20221118194904624

Solve:

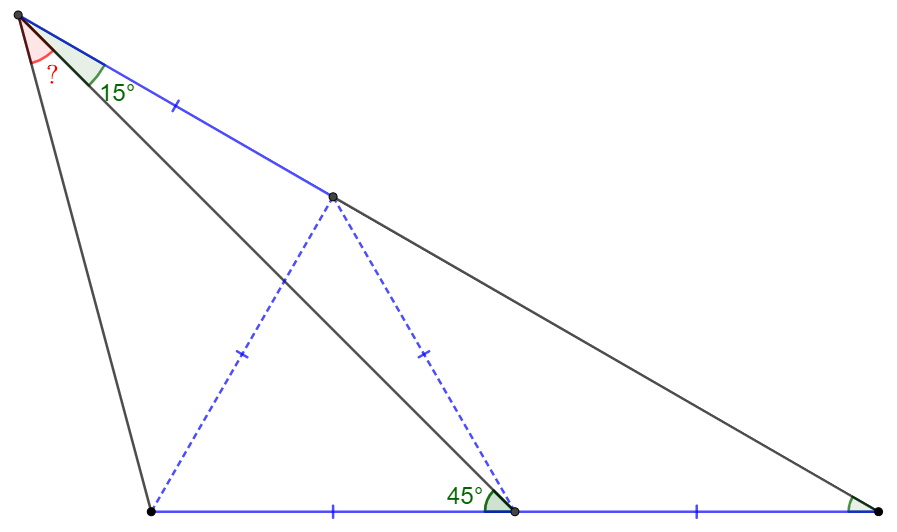
image-20221118194800792

11/23/2022

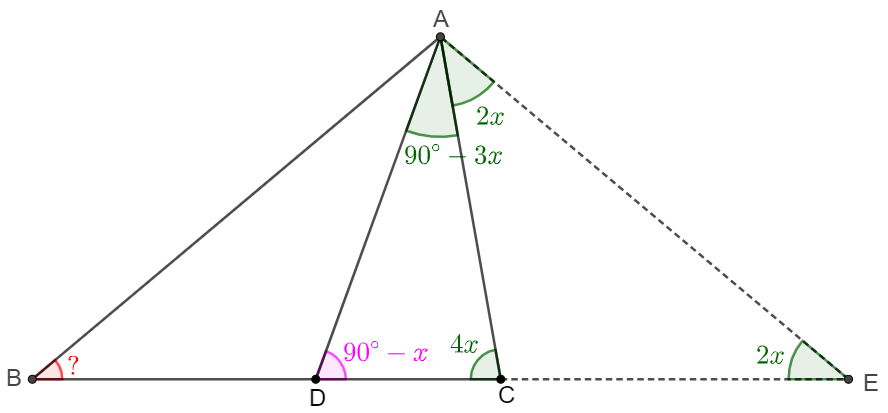
$D$ is a point in $\triangle{ABC}$ such that $\angle{ABD}=x, \angle{CBD}=30^{\circ}+x, \angle{ACD}=30^{\circ}-x, \angle{BCD}=30^{\circ}$. Find $\angle{CAD}$.

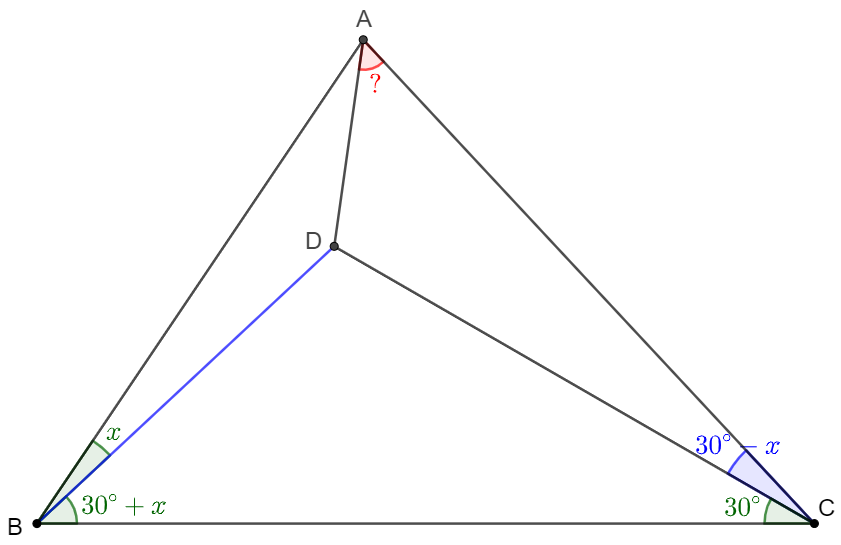
image-20221123172504214

Solve:

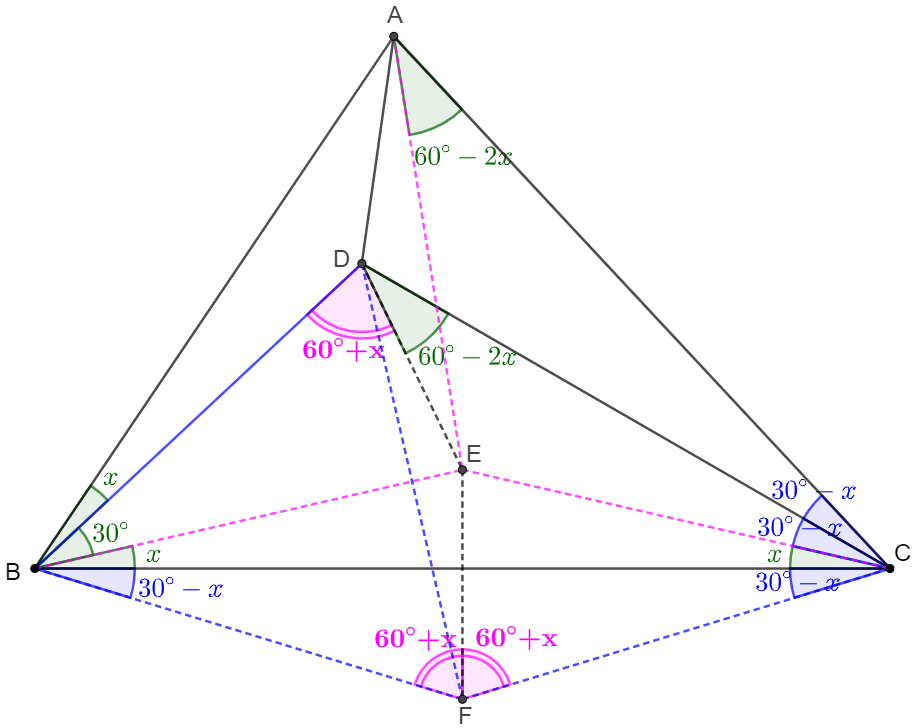
image-20221123175723964

. \(\begin{multline}\nonumber \shoveleft \text{Let } E \text{ be circumcenter of } \triangle{ABC}, \text{ Connect }AE, BE, CE\\ \shoveleft \implies AE=BE=CE\\ \shoveleft \begin{cases} \angle{AEC}=2\angle{ABC}=60^{\circ}+4x\implies \angle{EAC}=\angle{ECA}=60^{\circ}-2x \implies \angle{DCE}=30^{\circ}-x\\ \angle{BEC}=2\angle{BAC}=180^{\circ}-2x \implies \angle{EBC}=\angle{ECB}=x\\ \angle{AEB}=2\angle{ACB}=120^{\circ}-2x \implies \angle{EAB}=\angle{EBA}=30^{\circ}+x \implies DBE=30^{\circ}\\ \end{cases}\\ \shoveleft \text{Let } F \text{ be circumcenter of } \triangle{BCD}, \text{ Conect } BF, CF, DF, EF\\ \shoveleft \implies BF=CF=DF\\ \shoveleft \angle{DCB}=30^{\circ} \implies \angle{DFB}=60^{\circ} \implies \triangle{BDF} \text{ is equilateral}\\ \shoveleft \implies \angle{EBF}=30^{\circ}=\angle{DBE} \implies \angle{CBF}=\angle{BCF}=30^{\circ}-x\\ \shoveleft \implies \triangle{BDE}\cong\triangle{BFE}\cong\triangle{CFE}\\ \shoveleft \implies \angle{CFE}=\angle{BFE}=\angle{BDE}=\cfrac{180^{\circ}-2\angle{CBF}}{2}=\cfrac{180^{\circ}-60^{\circ}+x}{2}=60^{\circ}+2x\\ \shoveleft \implies \angle{CDE}=\angle{BDC}-\angle{BDE}=180^{\circ}-\angle{DBC}-\angle{DCB}-\angle{BDE}\\ \shoveleft=180^{\circ}-30^{\circ}-30^{\circ}-x-60^{\circ}-x=60^{\circ}-2x=\angle{EAC}\\ \shoveleft \implies A,C,D,E \text{ is cyclic} \implies \angle{DAE}=\angle{DCE}=30^{\circ}-x\\ \shoveleft \implies \angle{CAD}=60^{\circ}-2x+30^{\circ}-x=\bbox[5px, border: 1px solid black]{90^{\circ}-3x} \end{multline}\)

11/26/2022

$D$ is a point inside $\triangle{ABC}$ such that $\angle{ABD}=20^{\circ}, \angle{CBD}=10^{\circ}, \angle{ACD}=40^{\circ}, \angle{BCD}=30^{\circ}$, find $\angle{BAD}$.

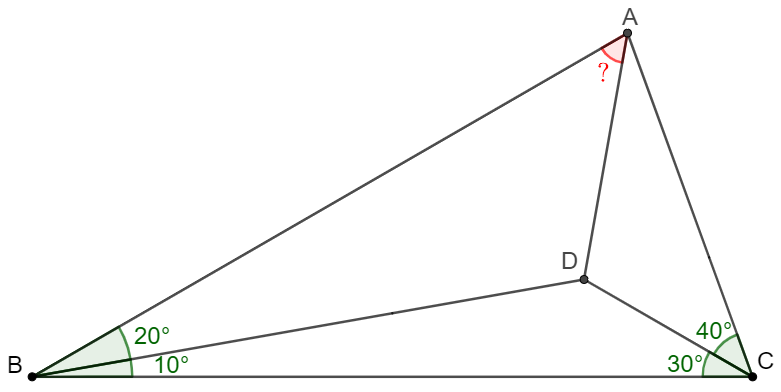
image-20221127024229865

Solve:

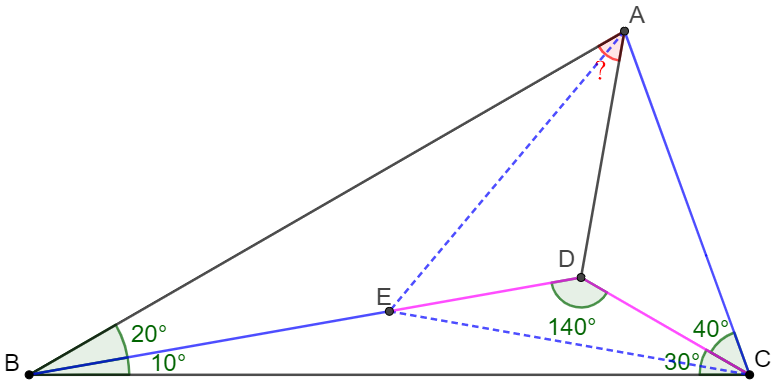
image-20221126211247849

. \(\begin{multline}\nonumber \shoveleft \text{ Let } E \text{ on BD such that } \angle{BAE}=\angle{ABD}=20^{\circ} \implies AE=BE, \angle{AEB}=140^{\circ}=2\angle{ACB}\\ \shoveleft \implies E \text{ is the circumcenter of }\triangle{ABC} \implies AE=BE=CE, \angle{AEC}=2\angle{ABC}=60^{\circ}\\ \shoveleft \implies \angle{CED}=20^{\circ}=\angle{DCE}, \triangle{AEC} \text{ is equilateral } \implies CD=ED, AE=CE\\ \shoveleft \implies \triangle{ADE} \cong \triangle{ADC} \implies \angle{EAD}=\angle{CAD}=\cfrac{60^{\circ}}{2}=30^{\circ}\\ \shoveleft \implies \angle{BAD}=20^{\circ}+30^{\circ}=\bbox[5px, border: 1px solid black]{50^{\circ}} \end{multline}\)

    © M∀TH Workout 2020-2021
    Search