2022/07/23

In quadrilateral $ABCD$, $AB=BC=CD, \angle{ABC}=70^{\circ}, \angle{BCD}=170^{\circ}$, find $\angle{BAD}$.

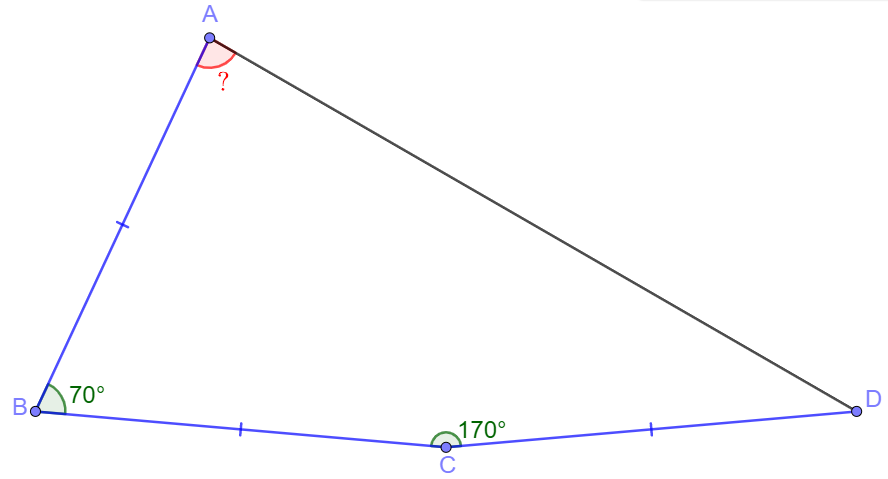
Solve:

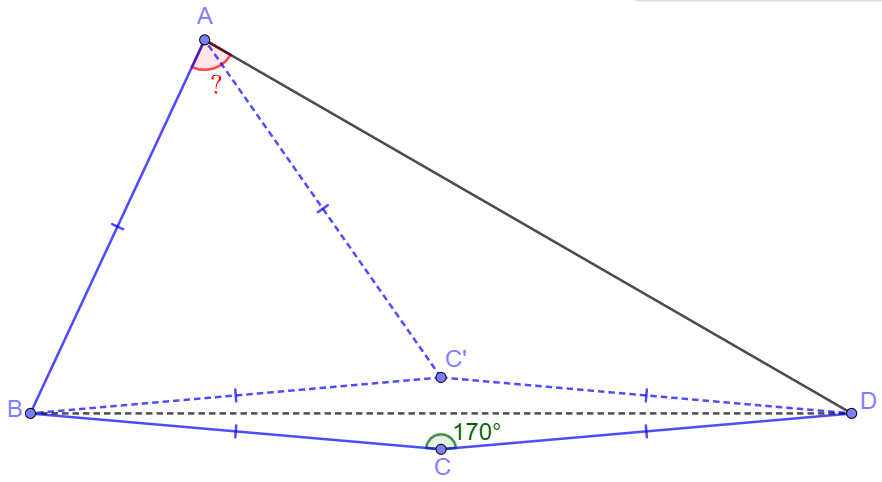
\(\begin{multline} \shoveleft \text{Connect }BD\text{ and reflect }C \text{ over }BD \text{ and get }C' \\\nonumber \shoveleft \implies AB=BC=CD=BC'=C'D, \angle{C'BD}=\angle{DBC}=\angle{C'DB}=\angle{BDC}=5^{\circ}\\ \shoveleft \implies \angle{ABC'}=60^{\circ}, C' \text{is circumcenter of } \triangle{ABD}\\ \shoveleft \implies \triangle{ABC'} \text{ is equilateral triangle}, \angle{ADB}=30^{\circ}\\ \shoveleft \implies \angle{C'AD}=\angle{C'DA}=25^{\circ}\\ \shoveleft \implies \angle{BAD}=\angle{BAC'}+\angle{C'AD}=60^{\circ}+25^{\circ}=\bbox[5px, border: 1px solid black]{85^{\circ}} \end{multline}\)