2022/06/07
$a,b,c > 0, a^{\frac{3}{2}} + b^{\frac{3}{2}} + c^{\frac{3}{2}}=1$, prove:
(1) $abc \le \dfrac{1}{9}$ (2) $\dfrac{a}{b+c} + \dfrac{b}{c+a} + \dfrac{c}{a+b} \le \dfrac{1}{2\sqrt{abc}}$
prove: \(\begin{multline} \shoveleft \text{(1)} \\ \shoveleft G_3=\sqrt[3]{x_1x_2x_3}, A_3=\dfrac{x_1+x_2+x_3}{3}, Gn \le An \\ \shoveleft a^{\frac{3}{2}} + b^{\frac{3}{2}} + c^{\frac{3}{2}}=1 \implies \dfrac{a^{\frac{3}{2}} + b^{\frac{3}{2}} + c^{\frac{3}{2}}}{3}=\dfrac{1}{3} \\ \shoveleft \implies \sqrt[3]{a^{\frac{3}{2}}b^{\frac{3}{2}}c^{\frac{3}{2}}}=(abc)^{\frac{1}{2}} \le \dfrac{1}{3} \\ \shoveleft \implies abc \le \dfrac{1}{9} \blacksquare \\ \shoveleft \text{(2)} \\ \shoveleft \dfrac{a}{b+c} + \dfrac{b}{c+a} + \dfrac{c}{a+b}\le \dfrac{a}{2\sqrt{bc}} + \dfrac{b}{2\sqrt{ca}} + \dfrac{c}{2\sqrt{ab}}\\ \shoveleft \implies \dfrac{a}{b+c} + \dfrac{b}{c+a} + \dfrac{c}{a+b} \le \dfrac{a^{\frac{3}{2}}+b^{\frac{3}{2}}+c^{\frac{3}{2}}}{2\sqrt{abc}}=\dfrac{1}{2\sqrt{abc}} \blacksquare \\\nonumber \end{multline}\)
2022/06/21
In $\triangle{ABC}$, $D$ is a point on $BC$ so that $\angle{DAC}=60^{\circ}, \angle{ACB}=40^{\circ}, AC=BD$, find $\angle{ABC}$.
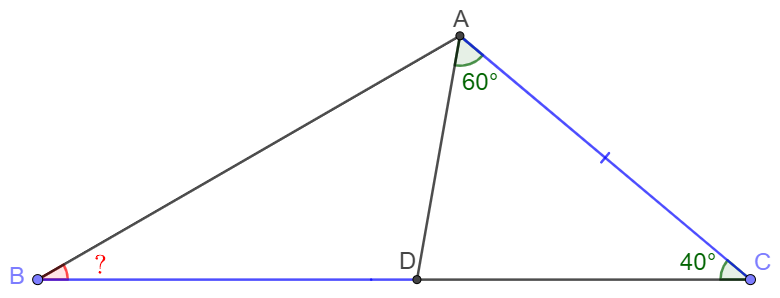
Solve:
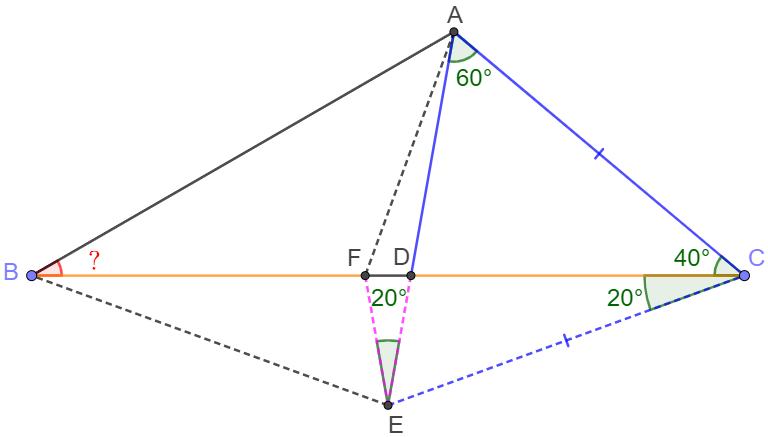 \(\begin{multline}\nonumber
\shoveleft \text{Easy to see } \angle{ADC}=180^{\circ}-60^{\circ}-40^{\circ}=80^{\circ}\\
\shoveleft \text{Extend } AD \text{ to } E \text{ so that } \triangle{ACE} \text{ is equilateral}.\\
\shoveleft \implies AE=AC=CE, \angle{DCE}=20^{\circ} \\
\shoveleft \text{Make } F \text{ on } BC \text{ so that } CE=EF\\
\shoveleft \implies CE=CF=AC=BD, \angle{CEF}=\angle{CFE}=80^{\circ}=\angle{ADC}=\angle{FDE}\\
\shoveleft \implies BF+DF=CD+DF, \angle{FED}=20^{\circ}, EF=DE, \angle{BFE}=\angle{CDE}\\
\shoveleft \implies BF=CD \\
\shoveleft \implies \triangle{BEF}\cong \triangle{CED}\\
\shoveleft \implies BE=CE=AE\\
\shoveleft \implies E \text{ is the circumcenter of } \triangle{ABC} \\
\shoveleft \implies \angle{ABC} = \dfrac{\angle{AEC}}{2}=\bbox[1px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Easy to see } \angle{ADC}=180^{\circ}-60^{\circ}-40^{\circ}=80^{\circ}\\
\shoveleft \text{Extend } AD \text{ to } E \text{ so that } \triangle{ACE} \text{ is equilateral}.\\
\shoveleft \implies AE=AC=CE, \angle{DCE}=20^{\circ} \\
\shoveleft \text{Make } F \text{ on } BC \text{ so that } CE=EF\\
\shoveleft \implies CE=CF=AC=BD, \angle{CEF}=\angle{CFE}=80^{\circ}=\angle{ADC}=\angle{FDE}\\
\shoveleft \implies BF+DF=CD+DF, \angle{FED}=20^{\circ}, EF=DE, \angle{BFE}=\angle{CDE}\\
\shoveleft \implies BF=CD \\
\shoveleft \implies \triangle{BEF}\cong \triangle{CED}\\
\shoveleft \implies BE=CE=AE\\
\shoveleft \implies E \text{ is the circumcenter of } \triangle{ABC} \\
\shoveleft \implies \angle{ABC} = \dfrac{\angle{AEC}}{2}=\bbox[1px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
2022/06/24
In quadrileteral $ABCD$, $BC=CD, \angle{ABD}=30^{\circ}, \angle{ACD}=38^{\circ}, \angle{BAC}=22^{\circ}$, find $\angle{CAD}$.
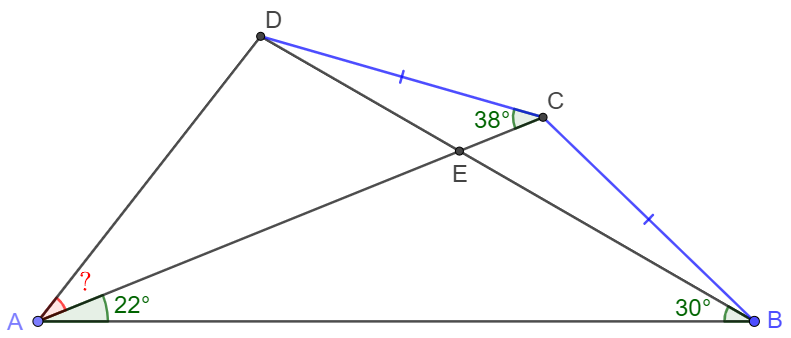
Solve:
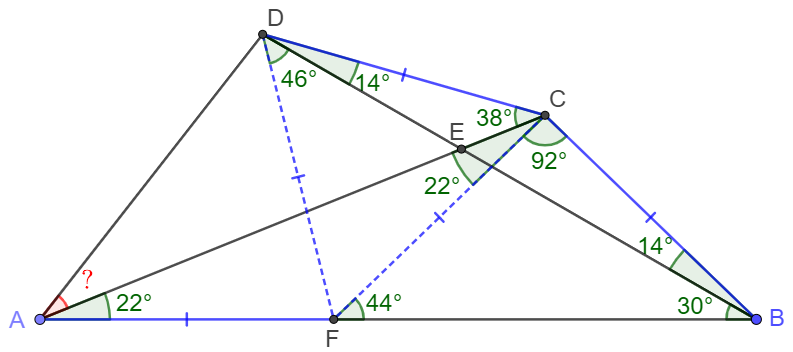 \(\begin{multline}\nonumber
\shoveleft \angle{CDB}=\angle{BAC}+\angle{ABD}-\angle{ACD}=14^{\circ}=\angle{CBD}\\
\shoveleft \implies \angle{BCD}=180^{\circ}-2*14^{\circ}-38^{\circ}=114^{\circ}\\
\shoveleft \text{Make } F \text{ on } AB \text{ so that } CF=BC=CD\\
\shoveleft \implies \angle{CFB}=\angle{CBF}=30^{\circ}+14^{\circ}=44^{\circ}\\
\shoveleft \implies \angle{FCB}=180^{\circ}-2*44^{\circ}=92^{\circ}\\
\shoveleft \implies \angle{ACF}=114^{\circ}-92^{\circ}=22^{\circ}=\angle{BAC}\\
\shoveleft \implies \angle{DCF}=38^{\circ}+22^{\circ}=60^{\circ}, AF=CF\\
\shoveleft \implies \triangle{CDF} \text{ is equilateral triangle}\\
\shoveleft \implies \angle{CFD}=60^{\circ}, CF=DF=AF\\
\shoveleft \implies F \text{ is circumcenter of } \triangle{ACD}\\
\shoveleft \implies \angle{CAD}=\dfrac{\angle{CFD}}{2}=\dfrac{60^{\circ}}{2}=\bbox[1px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \angle{CDB}=\angle{BAC}+\angle{ABD}-\angle{ACD}=14^{\circ}=\angle{CBD}\\
\shoveleft \implies \angle{BCD}=180^{\circ}-2*14^{\circ}-38^{\circ}=114^{\circ}\\
\shoveleft \text{Make } F \text{ on } AB \text{ so that } CF=BC=CD\\
\shoveleft \implies \angle{CFB}=\angle{CBF}=30^{\circ}+14^{\circ}=44^{\circ}\\
\shoveleft \implies \angle{FCB}=180^{\circ}-2*44^{\circ}=92^{\circ}\\
\shoveleft \implies \angle{ACF}=114^{\circ}-92^{\circ}=22^{\circ}=\angle{BAC}\\
\shoveleft \implies \angle{DCF}=38^{\circ}+22^{\circ}=60^{\circ}, AF=CF\\
\shoveleft \implies \triangle{CDF} \text{ is equilateral triangle}\\
\shoveleft \implies \angle{CFD}=60^{\circ}, CF=DF=AF\\
\shoveleft \implies F \text{ is circumcenter of } \triangle{ACD}\\
\shoveleft \implies \angle{CAD}=\dfrac{\angle{CFD}}{2}=\dfrac{60^{\circ}}{2}=\bbox[1px, border: 1px solid black]{30^{\circ}}
\end{multline}\)
2022/06/25
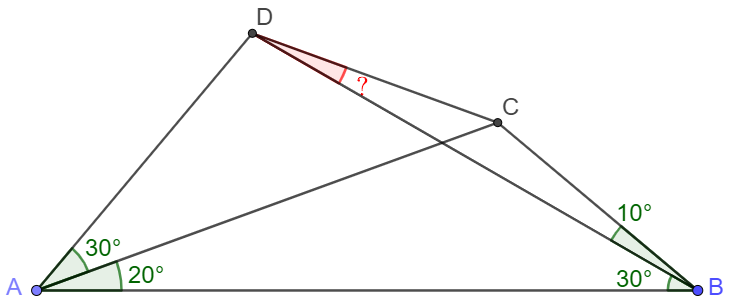
In quadrilateral $ABCD$, $\angle{CAD}=30^{\circ}, \angle{CAB}=20^{\circ}, \angle{ABD}=30^{\circ}, \angle{CBD}=10^{\circ}$, find $\angle{BDC}$.
Solve:
 \(\begin{multline}\nonumber
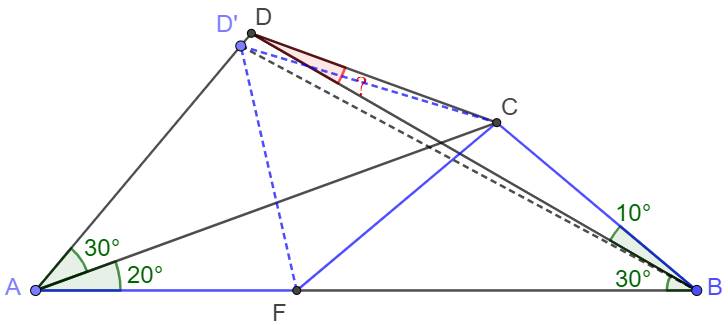
\shoveleft \text{Make } F \text{ on } AB \text{ so that } BC=CF, \text{Make } D' \text { on } AD \text { so that } AF=FD', \text{Connect } CD', BD'\\
\shoveleft \implies \angle{CFB}=\angle{CBF}=30^{\circ}+10^{\circ}=40^{\circ}, \angle{AD'F}=\angle{D'AF}=30^{\circ}+20^{\circ}=50^{\circ}\\
\shoveleft \implies \angle{ACF}=\angle{CFB}-\angle{CAF}=40^{\circ}-20^{\circ}=20^{\circ}=\angle{CAF}, \angle{AFD'}=80^{\circ}\\
\shoveleft \implies AF=FD'=CF=BC, \angle{CFD'}=180^{\circ}-\angle{AFD'}-\angle{CFB}=180^{\circ}-80^{\circ}-40^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{CFD'} \text{ is equilateral triangle}\\
\shoveleft \implies CD'=CF=CB\\
\shoveleft \implies C \text {is circumcenter of } \triangle{BFD'}\\
\shoveleft \implies \angle{FBD'}=\dfrac{\angle{FCD'}}{2}=\dfrac{60^{\circ}}{2}=30^{\circ}=\angle{FBD}\\
\shoveleft \implies D=D'\\
\shoveleft \implies \angle{BDC}=\angle{BD'C}=\angle{CBD'}=\angle{CBD}=\bbox[1px, border: 1px solid black]{10^{\circ}}
\end{multline}\)
\(\begin{multline}\nonumber
\shoveleft \text{Make } F \text{ on } AB \text{ so that } BC=CF, \text{Make } D' \text { on } AD \text { so that } AF=FD', \text{Connect } CD', BD'\\
\shoveleft \implies \angle{CFB}=\angle{CBF}=30^{\circ}+10^{\circ}=40^{\circ}, \angle{AD'F}=\angle{D'AF}=30^{\circ}+20^{\circ}=50^{\circ}\\
\shoveleft \implies \angle{ACF}=\angle{CFB}-\angle{CAF}=40^{\circ}-20^{\circ}=20^{\circ}=\angle{CAF}, \angle{AFD'}=80^{\circ}\\
\shoveleft \implies AF=FD'=CF=BC, \angle{CFD'}=180^{\circ}-\angle{AFD'}-\angle{CFB}=180^{\circ}-80^{\circ}-40^{\circ}=60^{\circ}\\
\shoveleft \implies \triangle{CFD'} \text{ is equilateral triangle}\\
\shoveleft \implies CD'=CF=CB\\
\shoveleft \implies C \text {is circumcenter of } \triangle{BFD'}\\
\shoveleft \implies \angle{FBD'}=\dfrac{\angle{FCD'}}{2}=\dfrac{60^{\circ}}{2}=30^{\circ}=\angle{FBD}\\
\shoveleft \implies D=D'\\
\shoveleft \implies \angle{BDC}=\angle{BD'C}=\angle{CBD'}=\angle{CBD}=\bbox[1px, border: 1px solid black]{10^{\circ}}
\end{multline}\)