2022-05-01
The square has side length $4$, find the area of the rectangle.
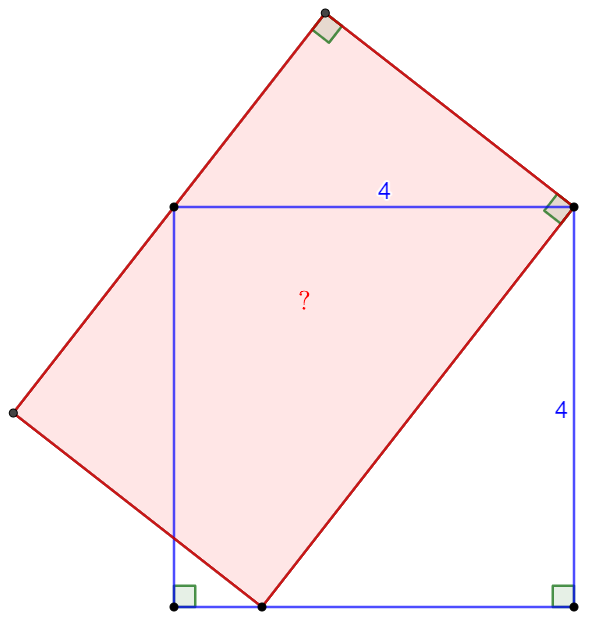
Solve:
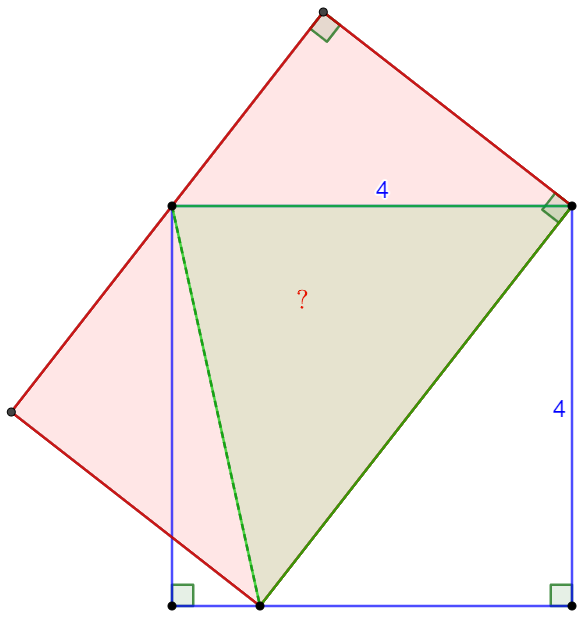
Area of the green triangle is half of the square, and is half of the rectangle. So the area of the rectangle is $\bbox[1px, border: 1px solid black]{16}$.
2022-05-02
A point inside the square forms a right triangle with two vertices of the square. Find the area of the red triangle.
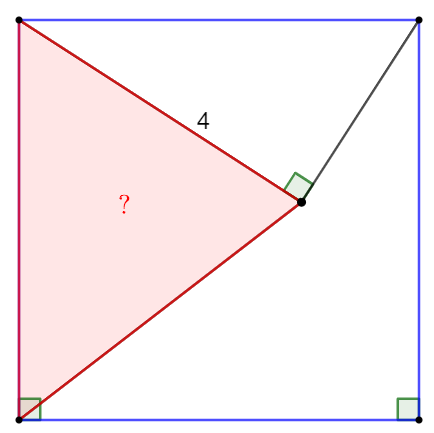
Solve:
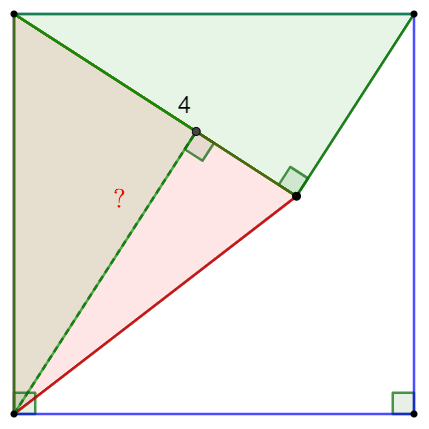
Make the height of the triangle as following, easy to know two green triangle is congruent to each other, so the height is also $4$. Then the triangle area is $\bbox[1px, border: 1px solid black]{8}$.
2022-05-03
Solve equation in positive integers $\dfrac{a}{b+c} + \dfrac{b}{c+a} + \dfrac{c}{a+b} = 4$
Solve:
2022-05-27
One hundred people line up to board a plane with 100 seats. The first person in line has lost his boarding pass, so he randomly chooses a seat. After that, each person entering the plane either sits in his/her assigned seat, if it is available, or, if not, chooses an unoccupied seat randomly. When the 100th passenger finally enters the plane, what is the probability that she finds her assigned seat unoccupied?
Solve 1:
The probability that the 100th passenger’s seat is occupied has nothing to do with who occupied it. So this probability is the same if the rule changes to following:
The first person in line randomly chooses a seat. After that, each person entering the plane sits in his/her assigned seat. If the first person has occupied it, then the first person randomly chooses another empty seat before the next person walks in.
By taking this rule, passenger 2nd to 99th will be seated in their assigned seats before the 100th passenger comes. At that moment the first passenger needs to choose bwetween two empty seats: his original assigned seat, or the seat of the 100th passenger. So the possibility of the 100th passenger finds her assigned seat unoccupied, is $\bbox[1px, border: 1px solid black]{0.5}$.
Solve 2:
This approach can also be based on the understanding of previous approach. Suppose $f(n)$ is the possibility that the $nth$ passenger can be seated in his/her assigned seat. Then we have $f(2)=\dfrac{1}{2}$ and we know \(\begin{multline} \shoveleft f(n)=\dfrac{1}{n} + \dfrac{n-2}{n} \cdot f(n-1) \\ \shoveleft \implies f(3)=\dfrac{1}{3} + \dfrac{1}{3} \cdot \dfrac{1}{2}=\dfrac{1}{2} \\ \shoveleft \text{Suppose } f(m)=\dfrac{1}{2} \text{ for } m=2,3,...,k \\ \shoveleft \implies f(k+1)=\dfrac{1}{k+1} + \dfrac{k-1}{k+1} \cdot \dfrac{1}{2}=\dfrac{k+1}{2(k+1)}=\dfrac{1}{2} \\ \shoveleft \implies f(n)=\dfrac{1}{2} \text{ for } n=1,2,... \implies f(100)=\bbox[1px, border: 1px solid black]{\dfrac{1}{2}} \end{multline}\)
Solve 3: \(\begin{multline} \shoveleft f(m)=\dfrac{1}{m} + \dfrac{m-2}{m}\dfrac{1}{m-1} + \dfrac{m-2}{m} \dfrac{m-3}{m-1} \dfrac{1}{m-2} + ... + \dfrac{m-2}{m} \dfrac{m-3}{m-1} \dfrac{1}{m-2} ... \dfrac{1}{2} \\ \shoveleft =\dfrac{1}{m} + \dfrac{m-2}{m(m-1)} + \dfrac{m-3}{m(m-1)} + ... + \dfrac{1}{m(m-1)} \\ \shoveleft =\dfrac{1}{m} + \dfrac{(m-2)(m-1)}{2m(m-1)} \\ \shoveleft =\dfrac{1}{m} + \dfrac{m-2}{2m} \\ \shoveleft =\dfrac{2+m-2}{2m}=\bbox[1px, border: 1px solid black]{\dfrac{1}{2}} \end{multline}\)
2022-05-28
What is the possibility that a rope is randomly cut into three pieces and they can form a triangle.
Solve:
Let the length of the rope is $1$, and the lengths of two pieces from both ends are $x$ and $y$. The middle piece is of length $1-x-y$.
Easy to see that $0<x<1$, $0<y<1$, and $0<x+y<1$.
To form a triangle, max length of each piece should be smaller than $\dfrac{1}{2}$, so we know $0<x<\dfrac{1}{2}, 0<y<\dfrac{1}{2}, 0<1-x-y<\dfrac{1}{2} \implies \dfrac{1}{2}<x+y<1$
To represent the restrictions in graph:
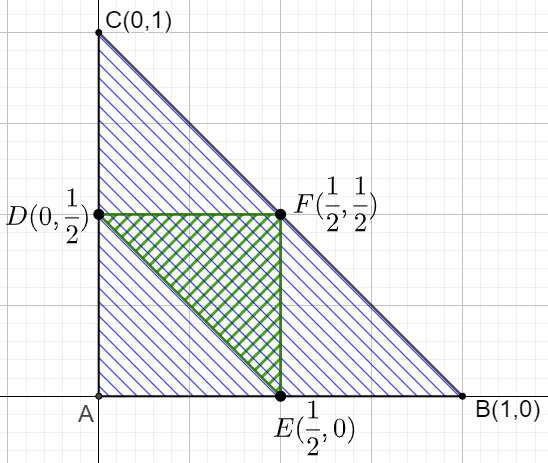
So the possibility is $\dfrac{S_{\triangle{DEF}}}{S_{\triangle{ABC}}}=\bbox[1px, border: 1px solid black]{\dfrac{1}{4}}$
2022-05-30
Choose $n$ points at random (uniformly and independently) on the circumference of a circle. Find the probability $p_n$ that all the points lie on a semicircle. (For instance, $p_1=p_2=1$). More generally, fix $\phi, 0 < \phi < 2\pi$ and find the probability that the $n$ points lie on an arc subtending an angle $\phi$.
Solve 1: