2022-03-11

Two circles are internally tangent at point $C$. $A$ is a point on outer circle and $AB, AD$ are two tangents to the inner circle, where $B, D$ are on the outer circle, and $E, F$ are the points of tangency on the inner circle. $EF, AC$ intersect at $G$. Prove: $\angle{EGB}=\angle{FGD}$.

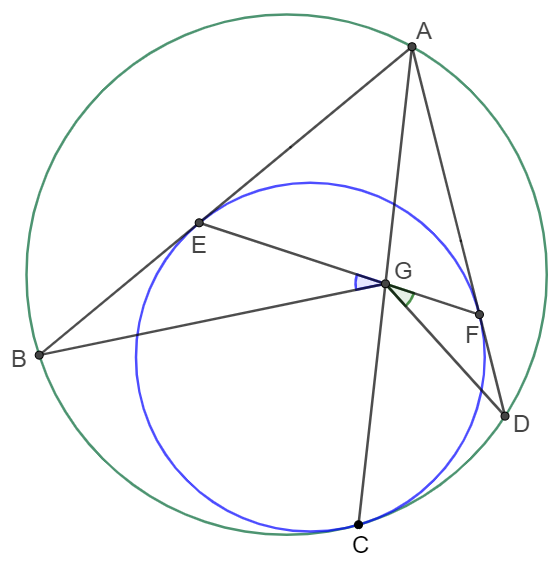
Prove 1:

Let the two circles be $c_1,c_2$. $AC$ and $c_1$ intersect at $Q$. The tangent at $C$ intersect with extended $EF$ at $P$.

$AB,AD$ are tangents to $c_1 \implies$ $EF$ is polar of $A$ to $c_1$. $P$ is on $EF$, according to La Hire Theorem, $A$ is on the polar of $P$ to $c_1$. That means $AC$ is the polar of $P$ to $c_1$. So the other point of tangency is $Q$ and $PQ$ is the tangent. Let the intersects of $PQ$ with $AB,AD$ be $M, N$ respectively.

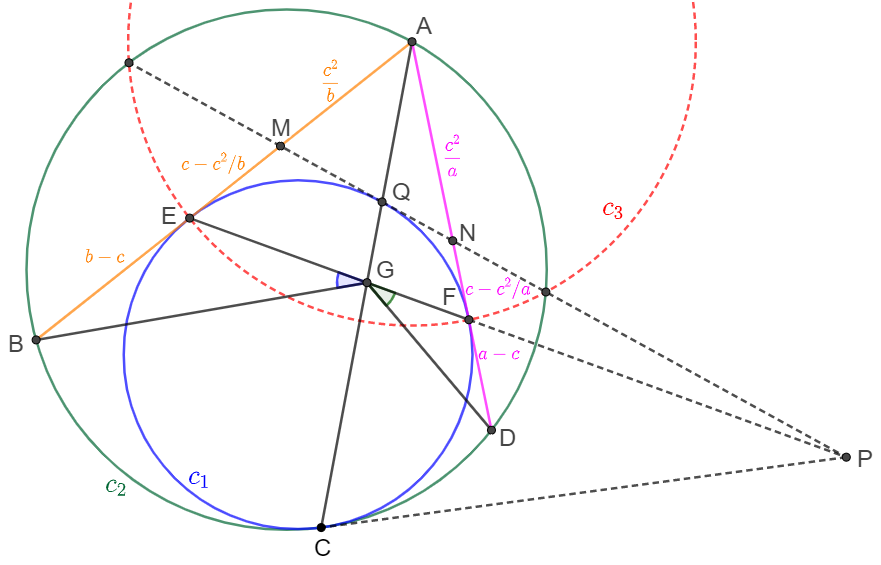
Suppose $AB=b, AD=a, AE=AF=c$. Make circle $C_3$ centered at $A$ with radius $c$. Easy to see that $c_1, c_3$ are orthogonal circles, so the inversion of $c_1$ to $c_3$ is $c_1$ itself, then we know the inversion of $C$ to $c_3$ is $Q$.

$c_2$ passes through the center $A$ of $c_3$, so the inversion of $c_2$ to $c_3$ is the line passing the intersects of $c_2$ and $c_3$. Since $C$ is the point of tangency of $c_1$ and $c_2$, then the inversion of $c_1$ must be the tangent to $c_2$ at $Q$, i.e., the line $PQ$. Suppose the intersects of $PQ$ with $AB, AD$ are $M, N$ respectively. So

$BE=b-c, AM=\dfrac{AE^2}{AB}=\dfrac{c^2}{b} \implies EM=c-\dfrac{c^2}{b}$

$DF=a-c, AN=\dfrac{AF^2}{AD}=\dfrac{c^2}{a} \implies FN=c-\dfrac{c^2}{a}$

Apply Menelaus’ Theorem to $\triangle{AEF}$ and line $PM$:

$\dfrac{EM}{MA} \dfrac{AN}{NF}\dfrac{FP}{EP}=1 \implies \dfrac{EP}{FP}=\dfrac{c-\dfrac{c^2}{b}}{\dfrac{c^2}{b}}\dfrac{\dfrac{c^2}{a}}{c-\dfrac{c^2}{a}}=\dfrac{b-c}{a-c}$

At mean time $DCEQ$ is cyclic harmonic quadrilateral，and $P$ is a point outside $c_1$，$G$ is the intersect of $EF$ and the polar of $P$ to $c_1$，from the property of harmonic quadrilateral we know：

$(E,F;P,G)=-1 \implies \dfrac{EP}{FP} \div \dfrac{EG}{FG}=1 \implies \dfrac{EG}{FG}=\dfrac{EP}{FP}=\dfrac{b-c}{a-c}=\dfrac{EP}{FP}$

So $\dfrac{BE}{DF}=\dfrac{EG}{FG}, AE=AF \implies \angle{BEG}=\angle{DFG} \implies \triangle{BEG} \sim \triangle{DFG} \implies \angle{EGB}=\angle{FGD} \blacksquare$

References

• Harmonic Geometry
• Poles and Polars
• Chapter 9 Projective Geometry from EGMO by Evan Chen

Chinese Version:

内外两个大小不等的圆内相切于点$C$。 $A$为外圆上一点，$AB,AD$为内圆两条切线，其中$B,D$在外圆上，$E,F$为内圆上对应的切点。$EF$与$AC$相交于$G$。证明：$\angle{EGB}=\angle{FGD}$。

证明:

设内外二圆为$c_1, c_2$。$AC$与$c_1$另一交点为$Q$，过$C$的外圆切线与EF延长线相交于$P$。

$AB,AD$为内圆切线，则$EF$所在直线为点$A$关于内圆$c_1$的极线。而$P$在$EF$所在直线上，根据 La Hire定理，$A$也在点$P$关于$c_1$的极线上，那么$AC$所在直线即为该极线，那么$PQ$为点$P$关于$c_1$的另一切线，$Q$即为相应切点。设该切线与$AB,AD$分别相交于$M,N$。

设$AB=b,AD=a,AE=AF=c$, 以$A$为圆、$c$ 为半径做圆$c_3$，显然可见，$c_1, c_3$是正交圆，根据反演性质，$c_1$关于$c_3$的反演为$c_1$本身，那么可知点$C$关于$c_3$的反演即为$Q$。

外圆$c_2$经过$c_3$的圆心$A$，则$c_2$关于$c_3$的反演为经过$c_2, c_3$二交点的直线。而$c_1, c_2$相切于$C$，根据反演性质，$c_1,c_2$关于$c_3$的反演也应该相切于$Q$，那么可见$c_2$关于$c_3$的反演即为经过$Q$点的关于$c_1$的切线，即$PQ$所在直线，则$PQ$与$AB,AD$的交点$M,N$即为$B,D$两点关于$c_3$的反演点。那么

$BE=b-c, AM=\dfrac{AE^2}{AB}=\dfrac{c^2}{b} \implies EM=c-\dfrac{c^2}{b}$

$DF=a-c, AN=\dfrac{AF^2}{AD}=\dfrac{c^2}{a} \implies FN=c-\dfrac{c^2}{a}$

对$\triangle{AEF}$及直线$PM$运用Menelaus定理：

$\dfrac{EM}{MA} \dfrac{AN}{NF}\dfrac{FP}{EP}=1 \implies \dfrac{EP}{FP}=\dfrac{c-\dfrac{c^2}{b}}{\dfrac{c^2}{b}}\dfrac{\dfrac{c^2}{a}}{c-\dfrac{c^2}{a}}=\dfrac{b-c}{a-c}$

同时，$DCEQ$为共圆$c_1$的调和四边形，$P$为$c_1$外点，$G$为$P$关于$c_1$的极线与$EF$的交点，根据调和四边形性质可知：

$(E,F;P,G)=-1 \implies \dfrac{EP}{FP} \div \dfrac{EG}{FG}=1 \implies \dfrac{EG}{FG}=\dfrac{EP}{FP}=\dfrac{b-c}{a-c}=\dfrac{EP}{FP}$

故 $\dfrac{BE}{DF}=\dfrac{EG}{FG}, AE=AF \implies \angle{BEG}=\angle{DFG} \implies \triangle{BEG} \sim \triangle{DFG} \implies \angle{EGB}=\angle{FGD} \blacksquare$

Prove 2:

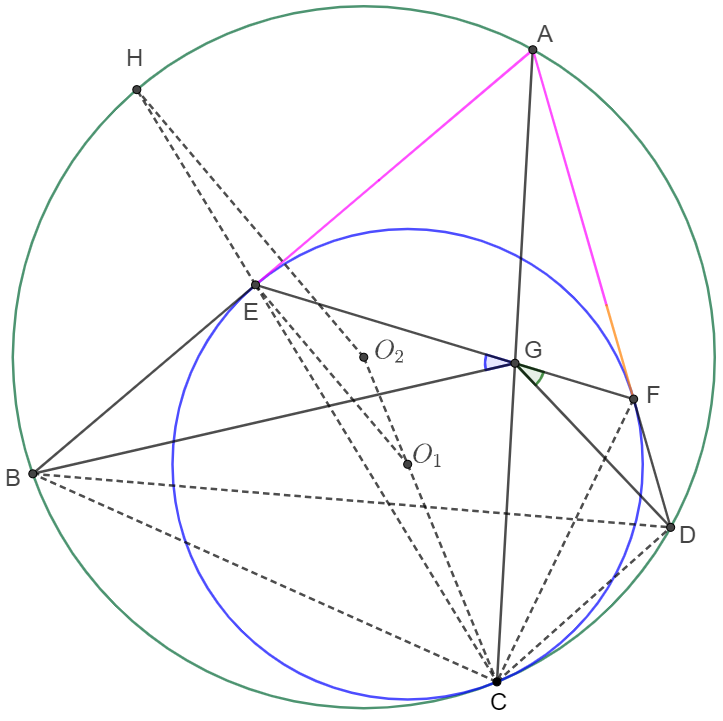
Let the two circles be $c_1,c_2$ and their centers are $O_1, O_2$ respectively.

Easy to know that $AE=AF, \angle{AEG}=\angle{AFG}$. From the Law of Sines:

$\dfrac{AG}{sin\angle{AEG}}=\dfrac{EG}{sin\angle{EAG}}=\dfrac{FG}{sin\angle{FAG}} \implies \dfrac{EG}{FG}=\dfrac{sin\angle{EAG}}{sin\angle{FAG}}=\dfrac{sin\angle{BAC}}{sin\angle{CAD}}=\dfrac{sin\angle{BDC}}{sin\angle{CBD}}=\dfrac{BC}{BD}$

Now we prove that $CE, CF$ bisect $\angle{ACB}, \angle{ACD}$ respectively:

Extended $CE$ and $c_2$ intersect at $H$. Apparently

$CO_2=HO_2, CO_1=EO_1 \implies \angle{CEO_1}=\angle{ECO_1}=\angle{CHO_2} \implies EO_1 \parallel HO_2$

So $EO_1 \perp AB \implies HO_2 \perp AB \implies \overset{\huge\frown}{AH}=\overset{\huge\frown}{HB} \implies \angle{BCE}=\angle{ACE}$, similarly $\angle{ACF}=\angle{DCF}$

$\implies \dfrac{AC}{AE}=\dfrac{BC}{BE}=\dfrac{AC}{AF}=\dfrac{CD}{DF} \implies \dfrac{BC}{BE}=\dfrac{CD}{DF} \implies \dfrac{BC}{CD}=\dfrac{BE}{DF}=\dfrac{EG}{FG}$

$\angle{BEG}=\angle{DFG} \implies \triangle{BEG} \sim \triangle{DFG} \implies \angle{EGB}=\angle{FGD}\blacksquare$

---

03/19/2022

In $\triangle{ABC}$, $\angle{A}=24^{\circ}, \angle{C}=30^{\circ}$, $D$ is on $AC$ so that $AB=CD$. Prove: $AB \cdot BC=AC \cdot BD$.

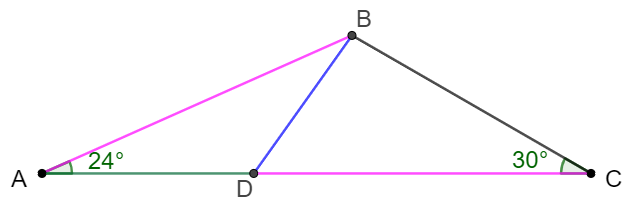
Prove:

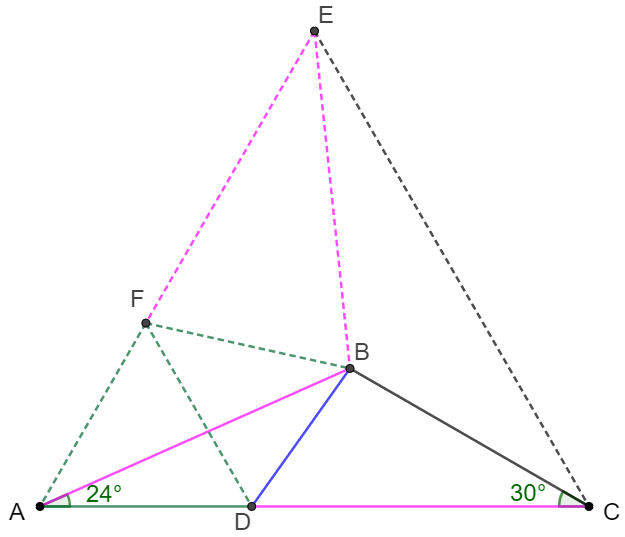
Make the mirror of $A$ along $BC$ to be $E$ so that $\triangle{ABC} \cong \triangle{EBC}$.

Easy to see that $AB=BE, AC=EC$ and $\triangle{ACE}$ is equilateral so $AC=AE, \angle{BEF}=60^{\circ}-\angle{BEC}=36^{\circ}$

Make $F$ on $AE$ so that $DF \parallel CE$ easy to know that $\triangle{ADF}$ is also equilateral, so

$AD=AF=DF \implies CD=AC-AD=AE-AF=EF=AB=BE $

$\implies \angle{EFB}=\angle{EBF}=\dfrac{180^{\circ}-36^{\circ}}{2}=72^{\circ} \implies \angle{ABF}=180^{\circ}-72^{\circ}-2*32^{\circ}=36^{\circ}=\angle{FAB} \implies DF=AF=BF$

$\implies \angle{FBD}=\dfrac{180^{\circ}-(180^{\circ}-\angle{AFD}-\angle{EFB})}{2}=66^{\circ} \implies \angle{ABD}=66^{\circ}-36^{\circ}=30^{\circ}$

$\implies \triangle{ABD} \sim \triangle{ACB} \implies \dfrac{BC}{AC}=\dfrac{BD}{AB} \implies AB \cdot BC=AC \cdot BD\blacksquare$

---

03/20/2022

Let $A_1=1998^{50}$, $A_{i+1}$ is the sum of all digits of $A_i$ for $i = 1, 2, … $ until $A_n < 10$. Find $A_n$.

Solve:

Let $A_i = \displaystyle \sum_{i=0}^{k}{a_i \cdot 10^i}$, then $A_{i+1} = \displaystyle \sum_{i=0}^{k}{a_i} \equiv A_i \text{ mod 9}$, and if $A_i \text{ mod 9} = 0$, then $A_{i+1}=9$

$1998^{50} \text{ mod 9} = (1998 \text{ mod 9})^{50} \text{ mod 9}=0^50 \text{ mod 9}=0$, so $A_n=\bbox[1px, border: 1px solid black]{9}$

---

03/30/2022

$AB=AC, \angle{ACB}=\angle{ABC}=40^{\circ}$ in $\triangle{ABC}$. Extend $AB$ to $D$ so that $AD=BC$. Find $\angle{ADC}$.

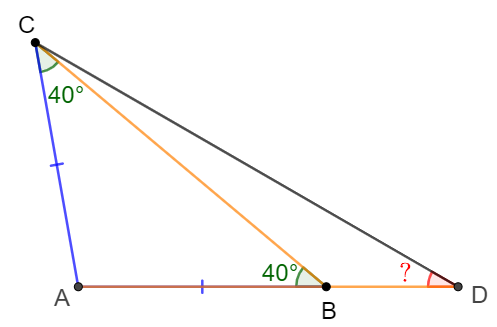
Solve:

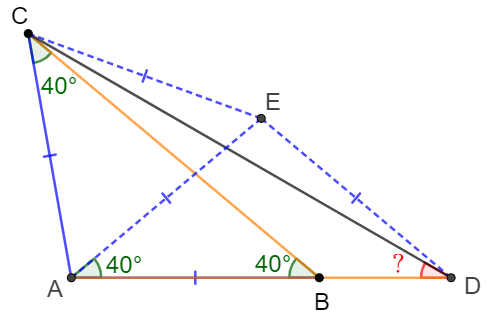
Select point $E$ so that $\angle{EAD}=\angle{EDA}=40^{\circ}$, connect $AE,CE,DE$.

Since $AD=BC$, $\triangle{ABC} \cong \triangle{ADE} \implies AC=AB=AE=DE, \angle{AED}=\angle{CAB}=100^{\circ}$

$\angle{CAE}=100^{\circ}-40^{\circ}=60^{\circ} \implies \triangle{ACE} \text{ is equilateral triangle } \implies CE=DE, \angle{CEA}=60^{\circ} $

$\implies \angle{CDE}=\angle{ECD}=\dfrac{180^{\circ}-60^{\circ}-100^{\circ}}{2}=10^{\circ} \implies \angle{ADC}=\angle{ADE}-\angle{CDE}=40^{\circ}-10^{\circ}=\bbox[1px, border: 1px solid black]{30^{\circ}}$

---