2022-02-13

$\triangle{ABC}, \angle{C}=75^{\circ}, \angle{BAC}=45^{\circ}, BD$ bisects $\angle{ABC}, AD=DE$, $AE$ and $BD$ intersect at $Q$, prove $Q$ bisects $BD$.

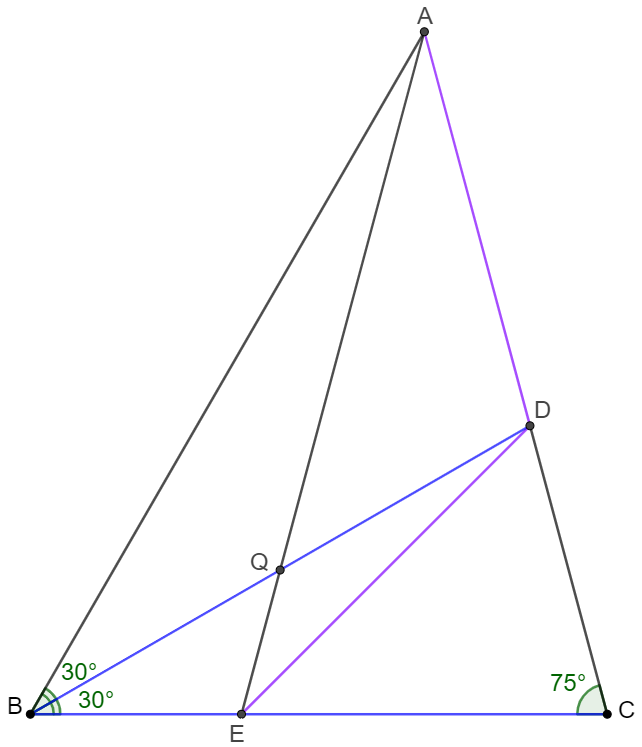
Prove:

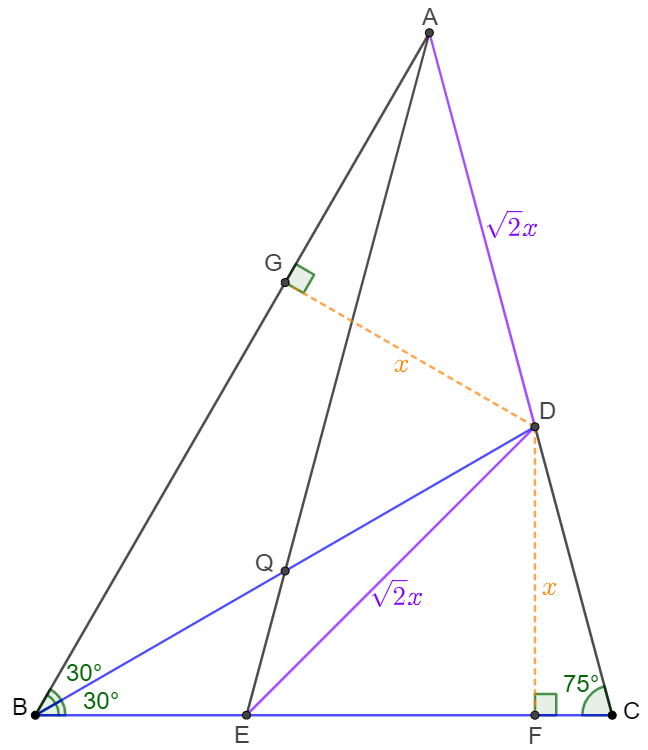
Make $DG \perp AB, DF \perp BC$, the perpendicular foots are $G$ and $F$ respectively. Let $DG=x$,

Easy to see that $AD=\sqrt{DG}=\sqrt{2}x=DE, BD=2x$

$\triangle{BDG} \cong \triangle{BDF} \implies DG=DF=x \implies \angle{DEF}=45^{\circ}=\angle{BAC} \implies \text{ABED are cyclic} $

$\implies \angle{EAD}=\angle{EBD}=30^{\circ} \implies \triangle{ABD} \sim \triangle{AQD} \implies \dfrac{BD}{AD}=\dfrac{AD}{QD} \implies AD^2=BD \cdot QD $

$\implies 2x^2=2x \cdot QD \implies QD=x=DG=DF=\dfrac{BD}{2} \implies BQ=DQ \blacksquare$

---