01/16/2022
$I$ is the incenter of $\triangle{ABC}$ and $D$ is the tangent point of the incircle with side $BC$. Points $E$ and $F$ are on side $BC$ so that $\angle{BAE}=\angle{ACB}, \angle{CAF}=\angle{ABC}$. $G$ and $H$ are incenters of $\triangle{ABE}$ and $\triangle{ACF}$ respectively. Prove that $AD$ is the Euler Line of $\triangle{GHI}$.
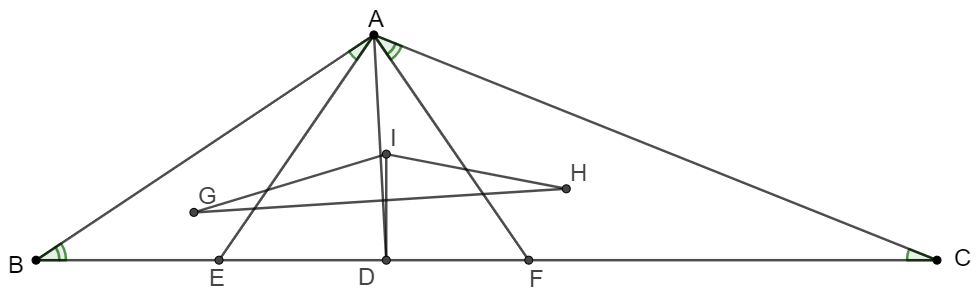
Prove:
Let $s=\dfrac{a+b+c}{2}, S_A=\dfrac{b^2+c^2-a^2}{2}, S_B=\dfrac{c^2+a^2-b^2}{2}, S_C=\dfrac{a^2+b^2-c^2}{2}$
$\overrightarrow{I}=\dfrac{a\overrightarrow{A}+b\overrightarrow{B}+c\overrightarrow{C}}{a+b+c}$
$\overrightarrow{G}=\dfrac{\dfrac{c^2}{a}\overrightarrow{A}+\dfrac{bc}{a}\overrightarrow{B}+c(\dfrac{c^2}{a^2}\overrightarrow{C}+(1-\dfrac{c^2}{a^2})\overrightarrow{B})}{\dfrac{c^2}{a}+\dfrac{bc}{a}+c}=\dfrac{c\overrightarrow{A}+(b+\dfrac{a^2-c^2}{a})\overrightarrow{B}+(\dfrac{c^2}{a})\overrightarrow{C}}{a+b+c}$
$\overrightarrow{H}=\dfrac{\dfrac{b^2}{a}\overrightarrow{A}+b((1-\dfrac{b^2}{a^2})\overrightarrow{C}+\dfrac{b^2}{a^2}\overrightarrow{B})+\dfrac{bc}{a}\overrightarrow{C}}{\dfrac{b^2}{a}+b+\dfrac{bc}{a}}=\dfrac{b\overrightarrow{A}+(\dfrac{b^2}{a})\overrightarrow{B}+(c+\dfrac{a^2-b^2}{a})\overrightarrow{C}}{a+b+c}$
$\overrightarrow{G_{GHI}}=\dfrac{\overrightarrow{G}+\overrightarrow{H}+\overrightarrow{I}}{3}=\dfrac{(a+b+c)\overrightarrow{A}+(2b+\dfrac{a^2+b^2-c^2}{a})\overrightarrow{B}+(2c+\dfrac{a^2+c^2-b^2}{a})\overrightarrow{C}}{a+b+c}$
$=\overrightarrow{A}+\dfrac{(a+b)^2-c^2}{a(a+b+c)}\overrightarrow{B}+\dfrac{(a+c)^2-b^2}{a(a+b+c)}\overrightarrow{C}=\overrightarrow{A}+\dfrac{a+b-c}{a}\overrightarrow{B}+\dfrac{a+c-b}{a}\overrightarrow{C}=\overrightarrow{A}+\dfrac{2s-2c}{a}\overrightarrow{B}+\dfrac{2s-2b}{a}\overrightarrow{C}$
To prove that $AD$ is the Euler Line of $\triangle{GHI}$, check if $\overrightarrow{G_{GHI}}$ is colinear with $\overrightarrow{A}$ and $\overrightarrow{D}=\dfrac{s-c}{a}\overrightarrow{B}+\dfrac{s-b}{a}\overrightarrow{C}$: \(\begin{align*} \begin{vmatrix} 1 & 0 & 0\\ 1 & \dfrac{s-c}{a} & \dfrac{s-b}{a}\\ 1 & \dfrac{2s-2c}{a} & \dfrac{2s-2b}{a} \end{vmatrix}&=\dfrac{s-c}{a}\dfrac{2s-2b}{a}-\dfrac{s-b}{a}\dfrac{2s-2c}{a}=0 \implies \overrightarrow{G_{GHI}}, \overrightarrow{A}, \overrightarrow{D} \text{ are collinear} \end{align*}\)
Now we prove that the circumcenter of $\triangle{GHI}$ is also collinear with $A,D$:
$cosB=\dfrac{a^2-b^2+c^2}{2ac}, sinB=\dfrac{2S}{ab} \implies x_A=c\cdot cosB=\dfrac{a^2-b^2+c^2}{2a}, y_A=c \cdot sinB=\dfrac{2S}{a}$
Let $A(\dfrac{a^2-b^2+c^2}{2a}, \dfrac{2S}{a}), B(0,0), C(a,0)$, Convert Barycentric Coordinates of point $G,H,I$ to Cartesian Coordinates:
\(\begin{align*} \begin{bmatrix} \overrightarrow{G} & \overrightarrow{H} & \overrightarrow{I} \end{bmatrix}&= \begin{bmatrix} \dfrac{a^2-b^2+c^2}{2a} & 0 & a\\ \dfrac{2S}{a} & 0 & 0\\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} \dfrac{c}{a+b+c} & \dfrac{b}{a+b+c} & \dfrac{a}{a+b+c}\\ \dfrac{b+\dfrac{a^2-c^2}{a}}{a+b+c} & \dfrac{\dfrac{b^2}{a}}{a+b+c} & \dfrac{b}{a+b+c}\\ \dfrac{\dfrac{c^2}{a}}{a+b+c} & \dfrac{c+\dfrac{a^2-b^2}{a}}{a+b+c} & \dfrac{c}{a+b+c} \end{bmatrix}\\ &= \begin{bmatrix} \dfrac{c(a-b+c)}{2a} & \dfrac{2a^2-b(a+b-c)}{2a} & \dfrac{a-b+c}{2} \\ \dfrac{2cS}{a(a+b+c)} & \dfrac{2bS}{a(a+b+c)} & \dfrac{2S}{a+b+c} \\ 1 & 1 & 1 \end{bmatrix} \end{align*}\) .
The Wolfram link of above calculation is here. Now we know that
$AB=c, AC=b, BC=a, BE=\dfrac{c^2}{a}, AE=AF=\dfrac{bc}{a}, CF=\dfrac{b^2}{a} \implies E(\dfrac{c^2}{a}, 0), F(\dfrac{a^2-b^2}{a}, 0)$
$x_G=X_{O_{\triangle{ABE}}}=\dfrac{BE\cdot x_A+AB \cdot x_E+AE \cdot x_B}{BE+AB+AE}=\dfrac{\dfrac{a^2-b^2+c^2}{2a}\dfrac{c^2}{a}+c\dfrac{c^2}{a}}{\dfrac{c^2}{a}+c+\dfrac{bc}{a}}=\dfrac{c(a-b+c)}{2a}$, link here
$y_G=Y_{O_{\triangle{ABE}}}=\dfrac{BE\cdot y_A+AB \cdot y_E+AE \cdot y_B}{BE+AB+AE}=\dfrac{\dfrac{2S}{a}\dfrac{c^2}{a}}{\dfrac{c^2}{a}+c+\dfrac{bc}{a}}=\dfrac{2cS}{a(a+b+c)}$, link here
$x_H=X_{O_{\triangle{ACF}}}=\dfrac{AF \cdot x_C + FC \cdot x_A + CA \cdot x_F}{AF+FC+CA}=\dfrac{\dfrac{bc}{a}a+b\dfrac{a^2-b^2}{a}+\dfrac{b^2}{a}\dfrac{a^2-b^2+c^2}{2a}}{\dfrac{bc}{a}+\dfrac{b^2}{a}+b}=\dfrac{2a^2-ab-b^2+bc}{2a}$, link here
$y_H=Y_{O_{\triangle{ACF}}}=\dfrac{AF \cdot y_C + FC \cdot y_A + CA \cdot y_F}{AF+FC+CA}=\dfrac{\dfrac{b^2}{a}\dfrac{2S}{a}}{\dfrac{bc}{a}+\dfrac{b^2}{a}+b}=\dfrac{2bS}{a(a+b+c)}$, link here
$x_I=X_{O_{\triangle{ABC}}}=\dfrac{BC \cdot x_A+AB \cdot x_C}{a+b+c}=\dfrac{\dfrac{a^2-b^2+c^2}{2a}a+ac}{a+b+c}=\dfrac{a-b+c}{2}$
$y_I=X_{O_{\triangle{ABC}}}=\dfrac{BC \cdot y_A}{a+b+c}=\dfrac{\dfrac{2S}{a}a}{a+b+c}=\dfrac{2S}{a+b+c}$
From Circumcenter Wiki we get the formula to calculate the Cartesian Coordinates of circumcemter (See Matlab code below for details):
\(\begin{align*} {O_x}&=\dfrac{(x_A^2+y_A^2)(y_B-y_C)+(x_B^2+y_B^2)(y_C-y_A)+(x_C^2+y_C^2)(y_A-y_B)}{2[x_A(y_B-y_C)+x_B(y_C-y_A)+x_C(y_A-y_B)]} =\dfrac{\begin{vmatrix}x_A^2+y_A^2 & y_A & 1\\ x_B^2+y_B^2 & y_B & 1\\ x_C^2+y_C^2 & y_C & 1\end{vmatrix}}{2\begin{vmatrix}x_A & y_A & 1 \\ x_B & y_B & 1 \\ x_C & y_C & 1\end{vmatrix}} \\ &=\dfrac{a^3+a^2b+a^2c-ab^2+ac^2-b^3+b^2c-bc^2+c^3}{2a(a+b+c)} \\ {O_y}&=\dfrac{(x_A^2+y_A^2)(x_C-x_B)+(x_B^2+y_B^2)(x_A-x_C)+(x_C^2+y_C^2)(x_B-x_A)}{2[x_A(y_B-y_C)+x_B(y_C-y_A)+x_C(y_A-y_B)]} =\dfrac{\begin{vmatrix}x_A & x_A^2+y_A^2 & 1\\ x_B & x_B^2+y_B^2 & 1\\ x_C & x_C^2+y_C^2 & 1\end{vmatrix}}{2\begin{vmatrix}x_A & y_A & 1 \\ x_B & y_B & 1 \\ x_C & y_C & 1\end{vmatrix}} \\ &=-\dfrac{(a-b+c)(a+b-c)(a^2-b^2-c^2)}{8aS} \end{align*}\).
To prove that $O$ is collinear with $A, D$:
\(\begin{align*} \begin{vmatrix} 1 & \dfrac{a-b+c}{2} & 0\\ 1 & \dfrac{a^2-b^2+c^2}{2a} & \dfrac{2S}{a}\\ 1 & \dfrac{a^3+a^2b+a^2c-ab^2+ac^2-b^3+b^2c-bc^2+c^3}{2a(a+b+c)} & -\dfrac{(a-b+c)(a+b-c)(a^2-b^2-c^2)}{8aS} \end{vmatrix} = 0 \end{align*}\) .
So the points $G_{\triangle{GHI}}$ and $O_{\triangle{GHI}}$ are collinear with $A, D$, this means $AD$ is the Euler Line of $\triangle{GHI} \blacksquare$.
Here is the Matlab code for symbolic calculation:
syms a b c s S D a_x a_y b_x b_y c_x c_y o_x o_y_n o_y_d O_X_N O_Y_N O_D o_x_2 o_x_y_2 check_collinear
s = (a + b + c) / 2;
S = sqrt(s * (s - a) * (s - b) * (s - c));
a_x = (a - b + c ) / 2;
a_y = 2 * S / (a + b + c);
b_x = c * (a - b + c) / (2 * a);
b_y = 2 * c * S / (a * (a + b + c));
c_x = (2 * a ^ 2 - a * b - b ^ 2 + b * c) / (2 * a);
c_y = 2 * b * S / (a * (a + b + c));
% Use formular from wiki directly %
D = 2 * (a_x * (b_y - c_y) + b_x * (c_y - a_y) + c_x * (a_y - b_y));
[o_x_n, o_x_d] = numden(((a_x ^ 2 + a_y ^ 2) * (b_y - c_y) + (b_x ^ 2 + b_y ^ 2) * (c_y - a_y) + (c_x ^ 2 + c_y ^ 2) * (a_y - b_y)) / D);
[o_y_n, o_y_d] = numden(((a_x ^ 2 + a_y ^ 2) * (c_x - b_x) + (b_x ^ 2 + b_y ^ 2) * (a_x - c_x) + (c_x ^ 2 + c_y ^ 2) * (b_x - a_x)) / D);
pretty(simplify(o_x_n / o_x_d))
pretty(simplify(o_y_n / o_y_d))
factor(o_x_n)
factor(o_y_n)
% Use determinant approach %
O_X_N = [a_x ^ 2 + a_y ^ 2, a_y, 1; b_x ^ 2 + b_y ^ 2, b_y, 1; c_x ^ 2 + c_y ^ 2, c_y, 1];
O_Y_N = [a_x, a_x ^ 2 + a_y ^ 2, 1; b_x, b_x ^ 2 + b_y ^ 2, 1; c_x, c_x ^ 2 + c_y ^ 2, 1];
O_D = 2 * [a_x, a_y, 1; b_x, b_y, 1; c_x, c_y, 1];
pretty(simplify(det(O_X_N) / det(O_D)))
pretty(simplify(det(O_Y_N) / det(O_D)))
check_collinear = simplify(det([1, (a - b + c) / 2, 0; 1, (a^2 - b^2 + c^2) / (2 * a), (2 * S) / a; 1, o_x_n / o_x_d, o_y_n / o_y_d]));
pretty(check_collinear)
And here is the result:
>> solved
3 2 2 2 2 3 2 2 3
a + a b + a c - a b + a c - b + b c - b c + c
------------------------------------------------------
2 a (a + b + c)
4 2 2 2 2 2 4 3 2 2 3 4
a - 2 a b + 2 a b c - 2 a c + b - 2 b c + 2 b c - 2 b c + c
- -----------------------------------------------------------------------
2 a sqrt((a + b + c) (a + b - c) (a - b + c) (b - a + c))
ans =
[-1, a^3 + a^2*b + a^2*c - a*b^2 + a*c^2 - b^3 + b^2*c - b*c^2 + c^3]
ans =
[a - b + c, a + b - c, a^2 - b^2 - c^2]
3 2 2 2 2 3 2 2 3
a + a b + a c - a b + a c - b + b c - b c + c
------------------------------------------------------
8 a (a + b + c)
4 2 4 3 3 4
a - #3 + 2 a b c - #2 + b - 2 b c + #1 - 2 b c + c
- --------------------------------------------------------
4 4 4
8 a sqrt(- a + #3 + #2 - b + #1 - c )
where
2 2
#1 == 2 b c
2 2
#2 == 2 a c
2 2
#3 == 2 a b
3 3 3 4 4 4 4 4 4 5 5 5 2 3 3 2 2 3 3 2 2 2 2 2 2
-((a - b + c) (a #1 - b #1 + c #1 - 3 a b + 3 a b + a c - a c + b c + b c + a - b - c - 2 a b + 2 a b + 2 a c - 2 a c - 2 a b c - 4 a b c - a b #1
2 2 2 2 2 3 3 3 2
+ a b #1 + a c #1 + a c #1 - b c #1 + b c #1 + 2 a b c + 2 a b c - 2 a b c))/(4 a (a + b + c) #1)
where
#1 == sqrt((a + b + c) (a + b - c) (a - b + c) (b - a + c))
>> solved
3 2 2 2 2 3 2 2 3
a + a b + a c - a b + a c - b + b c - b c + c
------------------------------------------------------
2 a (a + b + c)
4 2 2 2 2 2 4 3 2 2 3 4
a - 2 a b + 2 a b c - 2 a c + b - 2 b c + 2 b c - 2 b c + c
- -----------------------------------------------------------------------
2 a sqrt((a + b + c) (a + b - c) (a - b + c) (b - a + c))
ans =
[-1, a^3 + a^2*b + a^2*c - a*b^2 + a*c^2 - b^3 + b^2*c - b*c^2 + c^3]
ans =
[a - b + c, a + b - c, a^2 - b^2 - c^2]
3 2 2 2 2 3 2 2 3
a + a b + a c - a b + a c - b + b c - b c + c
------------------------------------------------------
8 a (a + b + c)
4 2 4 3 3 4
a - #3 + 2 a b c - #2 + b - 2 b c + #1 - 2 b c + c
- --------------------------------------------------------
4 4 4
8 a sqrt(- a + #3 + #2 - b + #1 - c )
where
2 2
#1 == 2 b c
2 2
#2 == 2 a c
2 2
#3 == 2 a b
0
>>
01/21/2022
There are five stones $A, B, C, D, E$ in a pond. A frog can jump from one stone to any other stone except current one. It starts from stone $A$. What is the possibility that it is back on stone $A$ after $5$ jumps?
Solve 1:
The transfer matrix is:
\(\begin{align*} A= \begin{vmatrix} 0 & \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} \\ \dfrac{1}{4} & 0 & \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} \\ \dfrac{1}{4} & \dfrac{1}{4} & 0 & \dfrac{1}{4} & \dfrac{1}{4} \\ \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} & 0 & \dfrac{1}{4} \\ \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} & \dfrac{1}{4} & 0 \end{vmatrix} \implies A^5 = \begin{vmatrix} \dfrac{51}{256} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} \\ \dfrac{205}{1024} & \dfrac{51}{256} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} \\ \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{51}{256} & \dfrac{205}{1024} & \dfrac{205}{1024} \\ \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{51}{256} & \dfrac{205}{1024} \\ \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{205}{1024} & \dfrac{51}{256} \end{vmatrix} \end{align*}\).
So the possibility that the frog is back to stone $A$ is $\bbox[1px, border: 1px solid black]{\dfrac{51}{256}}$.
Solve 2:
- Jump 1,there are $4^1$ situations,$\dfrac{0}{4}$ on $A$. So $1-\dfrac{0}{4}=\dfrac{4}{4}$ on non-$A$.
- Jump 2, $\dfrac{4}{4^2}$ on $A$. So $1-\dfrac{4}{4^2}=\dfrac{4^2-4}{4^2}=\dfrac{12}{4^2}$ on non-$A$.
- Jump 3, $\dfrac{12}{4^3}$ on $A$. So $1-\dfrac{12}{4^3} = \dfrac{4^3-12}{4^3}=\dfrac{52}{4^3}$ on non-$A$.
- Jump 4, $\dfrac{52}{4^4}$ on $A$. So $1-\dfrac{52}{4^4}=\dfrac{4^4-52}{4^4}=\dfrac{204}{4^4}$ on non-$A$.
- Jump 5, $\dfrac{204}{4^5}=\dfrac{51}{256}$ on $A$.
So the possibility that the frog is back to stone $A$ is $\bbox[1px, border: 1px solid black]{\dfrac{51}{256}}$.