11/07/2021
Two problems with known answers:
-
With two characters a and b, there are 2^2 strings of length 2: aa, ab, ba, bb. For any strings of length 4 on character set {a, b}, it cannot contain all the strings of length 2 (aa, ab, ba, bb), since for a string of length 4, it has totally 3 substrings of length 2, less than 2^2. But for a character ring of length 4, for example a ring of abba, it can contain all 2-char strings aa, ab, ba, bb. Suppose the character set has cardinal N (i.e., N characters in total). What is the minimum length of a ring that contains all the strings of length m?
-
Primorial related to the corollary of Prime Number Theorem: $e= \displaystyle \lim_{n \to \infty}{(\prod_{k=1}^{\pi_{n}}{p_k})^{1/n}} = \displaystyle \lim_{n \to \infty}{(\prod_{k=1}^{\pi_{n}}{p_k})^{1/p_n}}$
11/08/2021
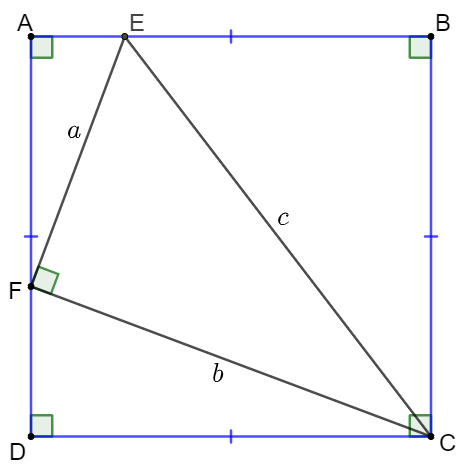
Right angle triangle $CEF$ inside square $ABCD$ has the sides of length $a,b,c$. Find the area of the square.
Solve:
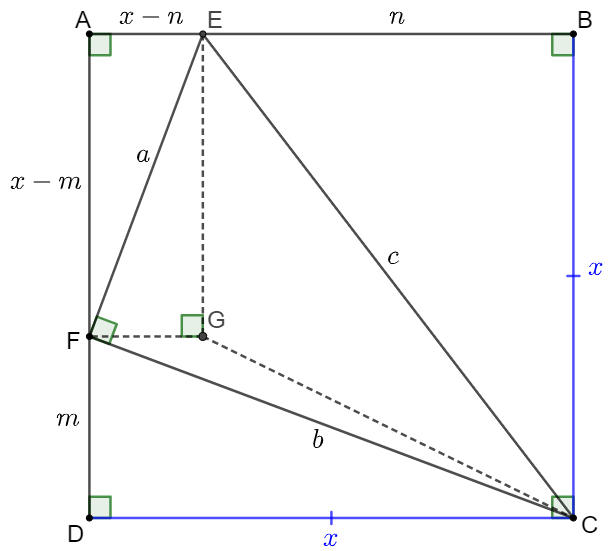
Let $AB=BC=CD=DA=x, DF=m, BE=n \implies AE=x-n, AF=x-m$
$\implies m^2+x^2=b^2, n^2+x^2=c^2, (x-m)^2+(x-n)^2=a^2$
$m^2+x^2=b^2, n^2+x^2=c^2, (x-m)^2+(x-n)^2=a^2 \implies (x-m)^2=b^2-2mx, (x-n)^2=c^2-2nx$
$\implies a^2=b^2+c^2-2(m+n)x \implies m+n=\dfrac{b^2}{x}$
Make $G$ inside $ABCD$ so that $EG \parallel AD, FG \parallel AB $
$\implies S_{\triangle{CEF}}=S_{\triangle{EFG}}+S_{\triangle{CFG}}+S_{\triangle{CEG}}=\dfrac{(x-m)(x-n)}{2} + \dfrac{(x-n)m}{2} + \dfrac{(x-m)n}{2}=\dfrac{ab}{2} \implies x^2=mn+ab$
$m^2+x^2=b^2, n^2+x^2=c^2 \implies m^2+n^2+2x^2=b^2+c^2=m^2+n^2+2mn+2ab=b^2+c^2$
$\implies (m+n)^2=b^2+c^2-2ab \implies \dfrac{b^4}{x^2}=b^2+c^2-2ab \implies x^2=\bbox[1px, border: 1px solid black]{\dfrac{b^4}{b^2+c^2-2ab}}$
11/09/2021
Solve the length AB:
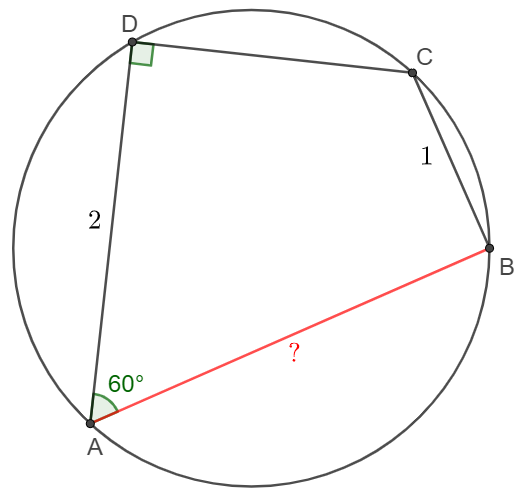
Solve:
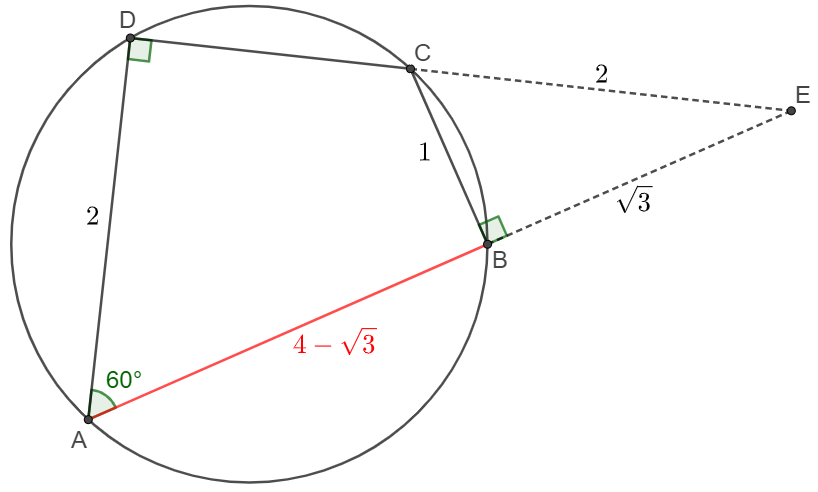
Let extended $DC$ and $AB$ intersects at $E$. Easy to see that $\triangle{EBC} \sim \triangle{EDA} \implies BC \perp AE$
$\angle{A}=60^{\circ} \implies \angle{E}=30^{\circ} \implies BE=\sqrt{3}BC=\sqrt{3}, CE=2BC=2, AE=\dfrac{AD}{BC}\cdot CE=4 $
$\implies AB=AE-BE=\bbox[1px, border: 1px solid black]{4-\sqrt{3}}$
11/10/2021
$81^{x^2+y}+81^{y^2+x}=\dfrac{2}{3}, x,y \in \mathbb{R}$, solve $x, y$.
Solve:
$81^{x^2+y} > 0, 81^{y^2+x} > 0 \implies 81^{x^2+y} + 81^{y^2+x} \ge 2\sqrt{81^{x^2+x+y+y^2}}$
$x^2+x+y^2+y=(x+\dfrac(1)(2))^2+(y+\dfrac{1}{2})^2-\dfrac{1}{2}\ge-\dfrac{1}{2}$
$\implies 81^{x^2+y} + 81^{y^2+x} \ge 2\sqrt{81^{x^2+x+y+y^2}} \ge 2*\sqrt{81^{-\frac{1}{2}}}=\dfrac{2}{3}$
It gets equality when $x=y=\bbox[1px, border: 1px solid black]{-\dfrac{1}{2}}$.
11/11/2021
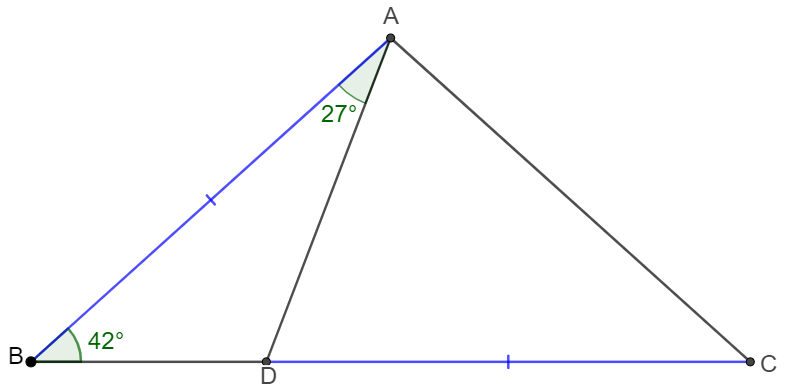
Prove: $AB=AC$
Prove:
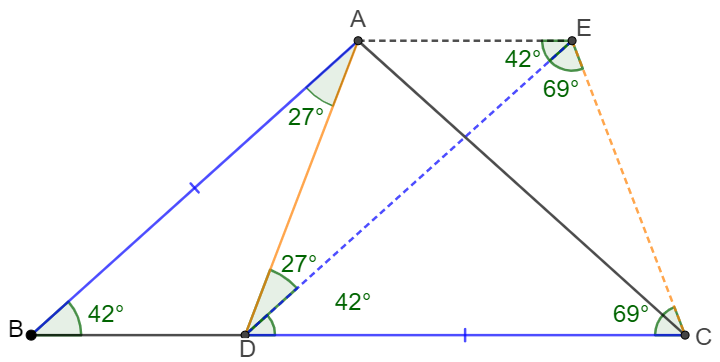
Make $AE \parallel BC$ and $DE \parallel AB$. Connect $CE$.
$DE \parallel AB \implies \angle{ADC}=\angle{ADE}+\angle{EDC}=\angle{BAD}+\angle{ABD}=27^{\circ}+42^{\circ}=69^{\circ}$
$DE \parallel AB, AE \parallel BC \implies DE=AB=CD \implies \angle{DCE}=\angle{DEC}=69^{\circ} $
$\implies \angle{ADC}=\angle{DCE} \implies AD=CE \implies \triangle{ACD} \cong \triangle{CED}\implies AC=DE=CD=AB \blacksquare$
11/12/2021
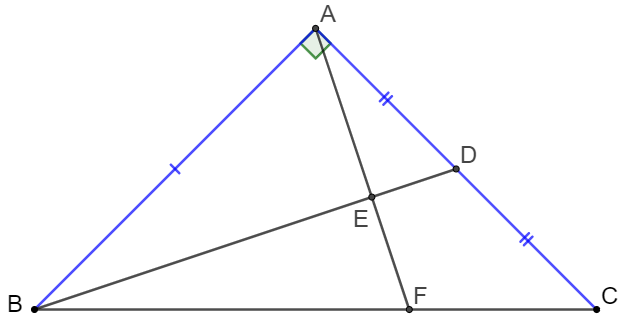
$\triangle{ABC}$ is an isosceles right triangle and $AD=CD, BF=2CF$, prove that $AF \perp BD$.
Prove:
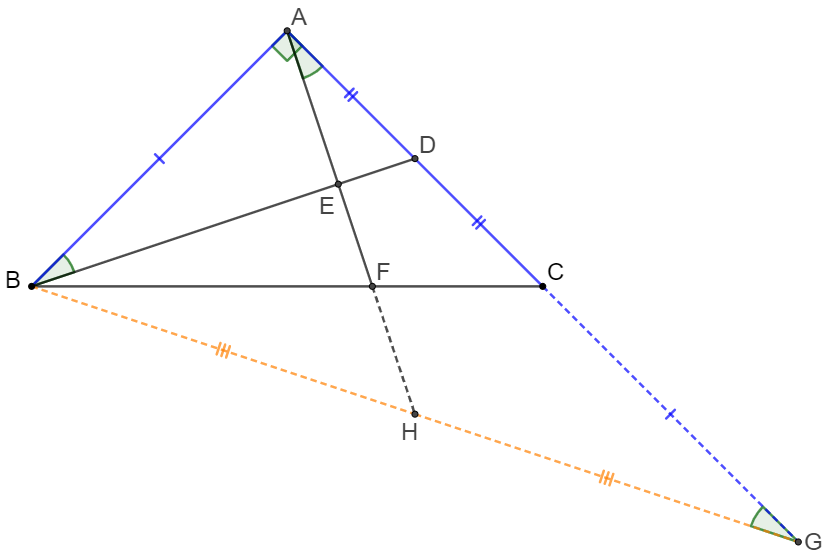
Extend $AC$ to $G$ so that $AC=CG$. Connect $BG$ and extend $AF$ so $AF$ and $BG$ intersects at $H$.
$BF=2CF \implies F$ is centroid of $\triangle{ABG} \implies BH=GH \implies AH=GH \implies \angle{HAG}=\angle{HGA}$
$AD=CD=\dfrac{AB}{2}, AB=AC=\dfrac{AG}{2} \implies \triangle{ABD} \sim \triangle{ABG} \implies \angle{ABD}=\angle{HGA}=\angle{HAG} $
$\implies \angle{AED}=180^{\circ}-\angle{HAG}-\angle{ADB}=180^{\circ}-\angle{ABD}-\angle{ADB}=90^{\circ} \implies AF \perp BD \blacksquare$
11/13/2021
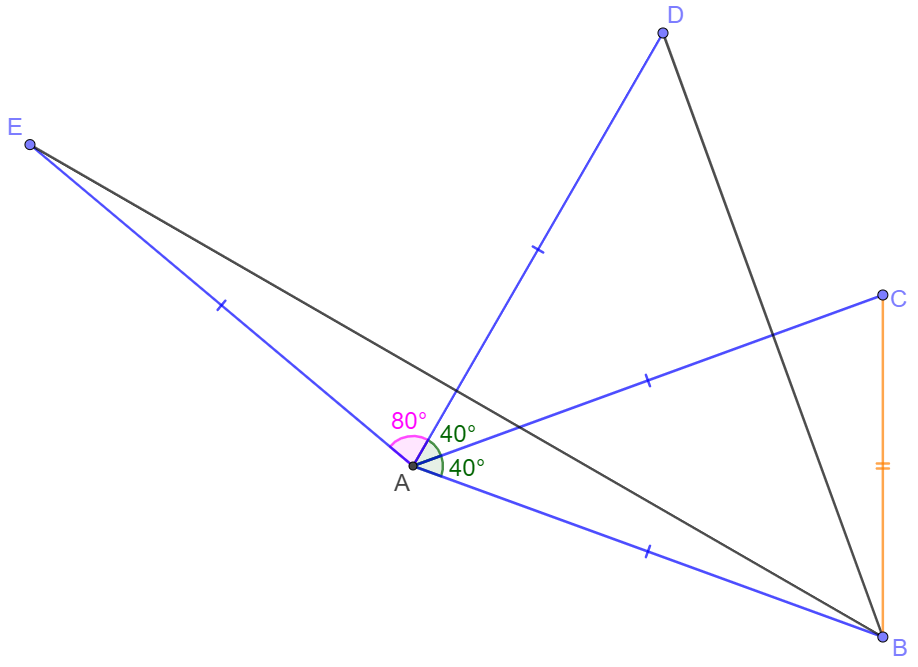
$AB=AC=AD=AE, \angle{BAC}=\angle{CAD}=40^{\circ}, \angle{DAE}=80^{\circ}$, prove $BE=BC+BD$.
Prove:
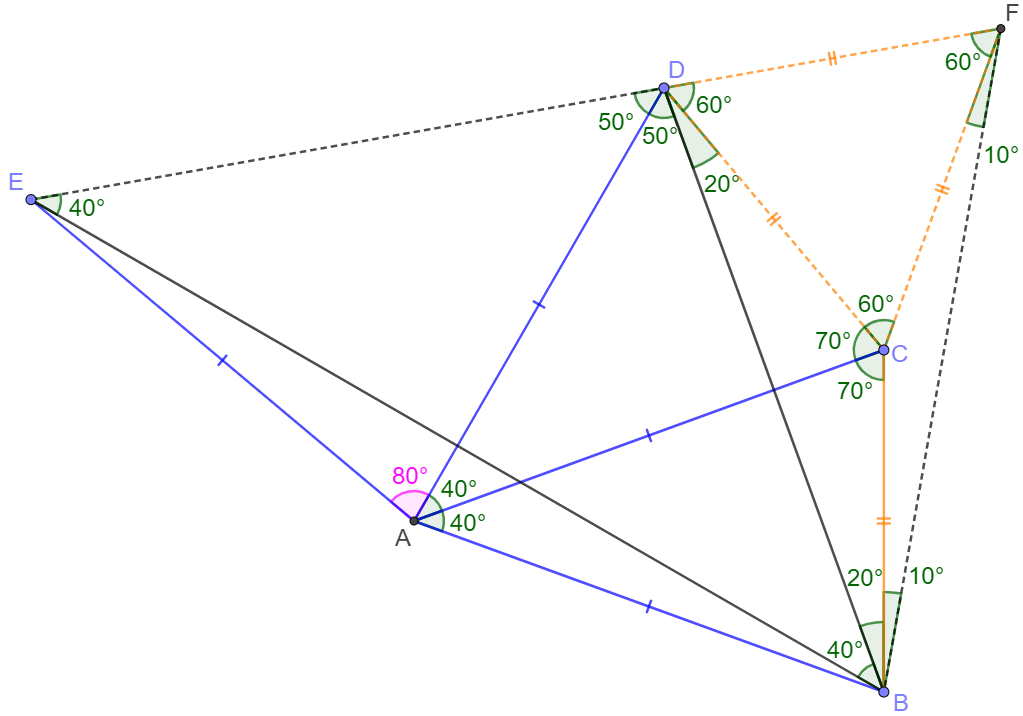
Angle chasing. The figure should be self-explained. $\blacksquare$
11/14/2021
$x+y+z=1, x^2+y^2+z^2=2, x^3+y^3+z^3=3, x^5+y^5+z^5=?$ (from MindYourDecisions)
Solve:
$k$-th degree power sum polynomial for variables $x_{1},x_{2},…x_{n}$ is:
$p_{k}(x_{1},x_{2},…,x_{n})=x_{1}^k+x_{2}^k+…+x_{n}^k$, so we know
$p_{1}(x,y,z)=x+y+z=p_{1}=1$
$p_{2}(x,y,z)=x^2+y^2+z^2=p_{2}=2$
$p_{3}(x,y,z)=x^3+y^3+z^3=p_{3}=3$
$k$-th degree elementary symmetric polynomial for $x_{1},x_{2},…x_{n}$ is:
$e_{0}(x_{1},x_{2},…,x_{n})=e_{0}=1$
$e_{1}(x_{1},x_{2},…,x_{n})=e_{1}=x_{1}+x_{2}+…+x_{n}$
$e_{2}(x_{1},x_{2},…,x_{n})=e_{2}=x_{1}x_{2}+x_{2}x_{3}+…+x_{n-1}x_{n}$
$e_{k}(x_{1},x_{2},…,x_{n})=e_{k}=\displaystyle \sum_{1 \le j_{1} \lt … \lt j_{k} \le n}{x_{j_{1}}x_{j_{2}}…x_{j_{k}}}$
$e_{r}(x_{1},x_{2},…,x_{n})=0 (r>n)$
$e_{k}$ is the sum of all terms where each term is the product of taking $k$ variables at a time.
When $n=3$, $k$-th degree elementary symmetric polynomial for $x,y,z$ is:
$e_{0}(x,y,z)=1$
$e_{1}(x,y,z)=x+y+z$
$e_{2}(x,y,z)=xy+yz+zx$
$e_{3}(x,y,z)=xyz$
$e_{r}(x,y,z)=0 (r>3)$
$f(t)=t^n+a_{n-1}t^{n-1}+…+a_{2}t^2+a_{1}t+a_{0}$ has $n$ roots $x_{1},x_{2},…,x_{n}$
$f(t)=(t-x_{1})(t-x_{2})…(t-x_{n})=t^n-e_{1}t^{n-1}+e_{2}t^{n-2}+…+(-1)^ne_{n}$
$f(x_{1})=0=x_{1}^n-e_{1}x_{1}^{n-1}+…+(-1)^ne_{n}$
$f(x_{2})=0=x_{2}^n-e_{1}x_{2}^{n-1}+…+(-1)^ne_{n}$
$…$
$f(x_{n})=0=x_{n}^n-e_{1}x_{n}^{n-1}+…+(-1)^ne_{n}$
Sum above $n$ equations to get
$0=p_{n}-e_{1}p_{n-1}+…+n(-1)^ne_{n}$
$\bbox[1px, border: 1px solid black]{ke_{k}=e_{k-1}p_{1}-e_{k-2}p_{2}+…+(-1)^{k-1}e_{0}p_{k}=\displaystyle \sum_{i=1}^{k}{(-1)^{i-1}e_{k-i}p_{i}} \qquad (n \ge k \ge 1)}$
Back to the problem:
$e_{0} = 1, e_{1} = x + y + z = 1, e_{2} = xy + yz + zx, e_{3} = xyz, e_{r}=0 \text{ } (r \gt 3)$
$p_{1} = 1 = x + y + z, p_{2} = 2 = x^2 + y^2 + z^2, p_{3} = 3 = x^3 + y^3 + z^3$
From Girard-Newton Identities we know
$2e_{2} = e_{1}p_{1} - e_{0}p_{2} \implies 2e_{2} = 1 * 1-1 * 2 = -1 \implies e_{2}=-\dfrac{1}{2}=xy+yz+zx$
$3e_{3} = e_{2}p_{1} - e_{1}p_{2} + e_{0}p_{3} = (-\dfrac{1}{2}) * 1 - 1 * 2 + 1 * 3 = \dfrac{1}{2} \implies e_{3} = \dfrac{1}{6} = xyz$
$4e_{4} = e_{3}p_{1} - e_{2}p2 + e_{1}p_{3} - e_{0}p_{4} = 0 = \dfrac{1}{6} * 1 - (-\dfrac{1}{2}) * 2 + 1 * 3 - p_{4} \implies p_{4} = \dfrac{25}{6} = x^4 + y^4 + z^4$
$5e_{5} = e_{4}p_{1} - e_{3}p_{2} + e_{2}p_{3} - e_{1}p_{4} + e_{0}p_{5} = 0 = 0 * 1 - \dfrac{1}{6} * 2 + (-\dfrac{1}{2}) * 3 - 1 * \dfrac{25}{6} + 1 * p_{5} \implies p_{5}=\bbox[1px, border: 1px solid black]{6} = x^5 + y^5 + z^5$
11/15/2021
100 boxes contain apples, oranges and bananas. Prove that we can choose 51 boxes in such a way that they contain at least half of all apples, and half of all oranges and half of all bananas. AOPS Link
Prove:
Lemma by Fedor Petrov: Any $2k$ pairs of positive reals $(a_i, b_i)$ can be partitioned into $2$ groups of $k$ pairs each, so that if $x$ is the sum of $a_i$ in the first group and $y$ is the sum of $a_i$ in the second group, then $ \lvert x - y \rvert \le \displaystyle \max_{i}{a_i}$. And the same inequality holds for $b_i$, i.e., if $m$ is the sum of $b_i$ in the first group and $n$ is the sum of $b_i$ in the second group, then $ \lvert m - n \lvert \le \displaystyle \max_{i}{b_i}$.
Proof of the Lemma:
The statement holds clearly for the case $k=1,2$. Assume it holds for $k=n$ and let’s prove it for $k=n+1$.
WLOG assume that $a_{2n+2} \ge a_{2n+1} \ge \displaystyle \max_{i=1}^{2n}{a_i}$. Due to the induction assumption used for the case $2n$ the following inequality must hold:
$ \lvert x - y \rvert \le a_{2n+1}$
Consider two cases:
- $b_{2n+2} \ge b_{2n+1}$
WLOG we assume $m \ge n$.
Then we add the pair $(a_{2n+1}, b_{2n+1})$ to the first group, and $(a_{2n+2}, b_{2n+2})$ to the second, so
$\lvert x + a_{2n+1} -y -a_{2n+2} \rvert \le \lvert x - y \rvert + \lvert a_{2n+1} - a_{2n+2} \rvert \le a_{2n+1} + a_{2n+2} - a_{2n+1} = a_{2n+2}$
If $m + b_{2n+1} \ge n + b_{2n+2}$ then
$\lvert m + b_{2n+1} -n -b_{2n+2} \rvert = m + b_{2n+1} - n - b_{2n+2} \le \displaystyle \max_{i}^{2n+2}{b_i}$
If $m + b_{2n+1} \le n + b_{2n+2}$ then
$\lvert m + b_{2n+1} -n -b_{2n+2} \rvert = n + b_{2n+2} - m - b_{2n+1} \le b_{2n+2} - b_{2n+1} \le \displaystyle \max_{i}^{2n+2}{b_i}$
For the case $b_{2n+1} \gt b_{2n+2}$ add the pairs in the reverse way, the rest is completely the same as in above case.
So the lemma is proved. $\blacksquare$
The last step is pretty obvious. Take two boxes, one box with the apple of the max weight, and the other box with the orange with the max weight. Applying the Lemma for $k=98$, with $a_i$ as weights of apples and $b_i$ as weights of oranges, and choose a group with larger weight of bananas in it. Add both those boxes into this group.
11/16/2021
In $\triangle{ABC}$, $AP=PQ=QC=a, BC=b, AB=33, AC=21, a, b \in \mathbb{Z^+}$, find $67b+a$.
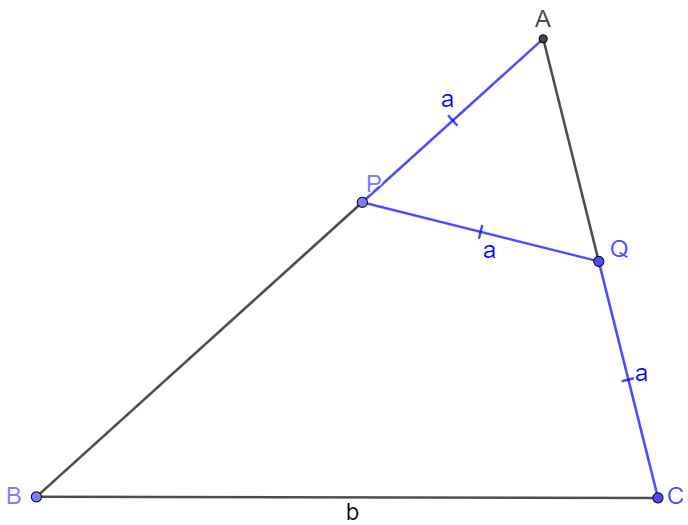
Solve:
Easy to see that $ AQ = 21 - a \implies 21-a-a \lt a \implies 21 \gt a \gt 7$
$cos(\angle{A})=\dfrac{21-a}{2a}=\dfrac{33^2+21^2-b^2}{2 * 33 * 21} \implies b^2=\dfrac{(33 * 21 + 33^2 + 21^2)a - 33 * 21^2}{a}=9 * 13 * 19 - \dfrac{3^3 * 7^2 * 11}{a}$
$b \in \mathbb{Z^+} \implies b^2 \in \mathbb{Z^+} \implies \dfrac{3^3 * 7^2 * 11}{a} \in \mathbb{Z^+}, 7 \lt a \lt 21 \implies$
- $a=9 \implies b^2=1684 = 4 * 421 \implies b \notin \mathbb{Z^+}$
- $a=11 \implies b^2=900 \implies b=30 \implies 67b+a=\bbox[1px, border: 1px solid black]{2021}$
11/17/2021
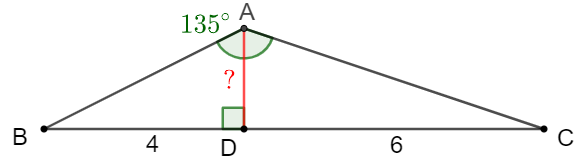
Solve:
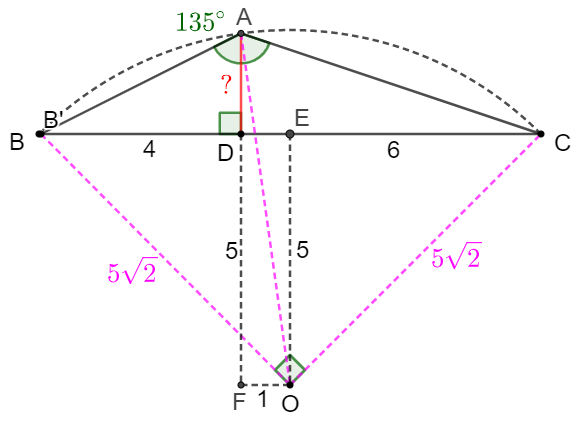
Let $O$ be the circumcenter of $\triangle{ABC}. \angle{BAC}=135^{\circ} \implies \angle{BOC}=90^{\circ} \implies BO=AO=CO=5\sqrt{2}$
Make $OE \perp BC, FO \parallel BC, AF \parallel EO \implies DE=FO=1, EO=DF=5 \implies AF=\sqrt{AO^2-FO^2}=7$
$\implies AD=AF-DF=7-5=\bbox[1px, border: 1px solid black]{2}$
11/18/2021
AMC 10A 2022 Problem 17: An architect is building a structure that will place vertical pillars at the vertices of regular hexagon $ABCDEF$, which is lying horizontally on the ground. The six pillars will hold up a flat solar panel that will not be parallel to the ground. The heights of the pillars at $A,B,$ and $C$ are $12, 9,$ and $10$ meters, respectively. What is the heigh, in meters, of the pillar at $E$?
Solve:
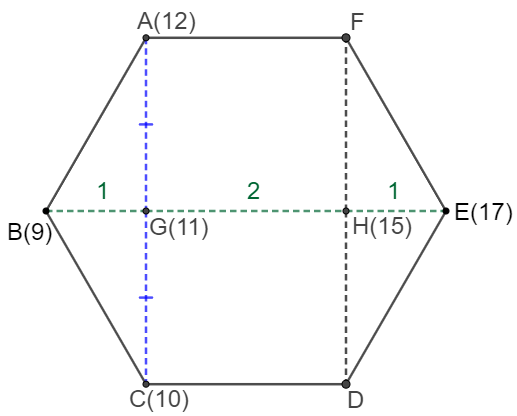
Connect $AC, DF$ and $BE$ and the intersections are $G$ and $H$.
$AG=CG \implies height_G = \dfrac{height_A+height_C}{2} = \dfrac{10+12}{2}=11$
$GH=2BG \implies height_H-height_G=2(height_G-height_B)=2*2=4 \implies height_G=4+height_G=15$
$ GH=2EH \implies height_H-height_G = 2(height_E-height_H)=4 \implies height_E-height_H=2 $
$\implies height_E=height_H+2=15+2=\bbox[1px, border: 1px solid black]{17}$
11/19/2021
$C$ is midpoint of side $AB$ in $\triangle{ABD}$ and $\angle{ACD}=45^{\circ}, \angle{B}=30^{\circ}$, find $\angle{A}$
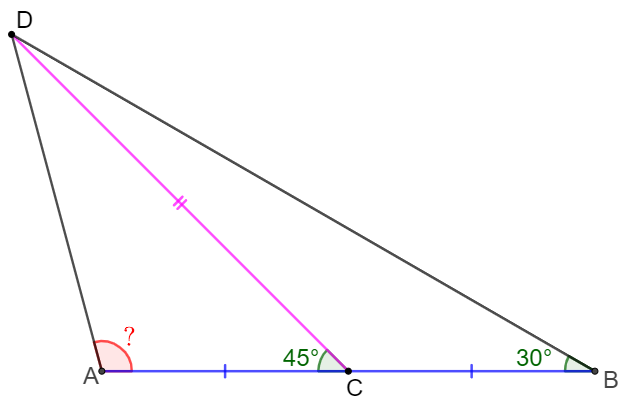
Solve:
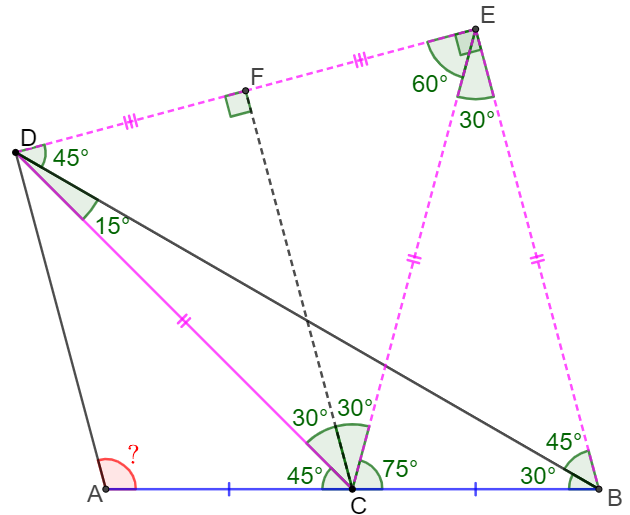
Make $E$ as circumcenter of $\triangle{BCD} \implies BE=CE=DE, \angle{BEC}=2\angle{BDC}=30^{\circ}, \angle{CED}=2\angle{CBD}=60^{\circ} $
$\implies \angle{BCE}=\angle{CBE}=75^{\circ} \implies \angle{DBE}=\angle{BDE}=45^{\circ} \implies BE \perp DE$.
Make $CF \perp DE \implies DF=EF \implies AD \parallel BE \implies \angle{A}=180^{\circ}-\angle{CBE}=\bbox[1px, border: 1px solid black]{105^{\circ}}$
11/20/2021
AMC 12A Problem 24: Convex quadrilateral $ABCD$ has $AB=18, \angle{A}=60^{\circ}$, and $AB \parallel CD$. In some order, the lengths of the four sides form an arithmetic progression, and side $AB$ is a side of maximum length. The length of another side is $a$. What is the sum of all possible values of $a$?
凸四边形 $ABCD$ 中 $AB=18, \angle{A}=60^{\circ}$, 且 $AB \parallel CD$. 四边形的四边长按某一顺序组成等差数列,而$AB$ 是最长的边。另一条边长为$a$。 问:$a$的所有可能值之和为多少?
11/21/2021
Rectangle $ABCD$ has $CG$ as bisector of $\angle{ACD}$, $CF$ as bisector of $\angle{ACB}$. $AG=2, AF=3$, find $AC$.
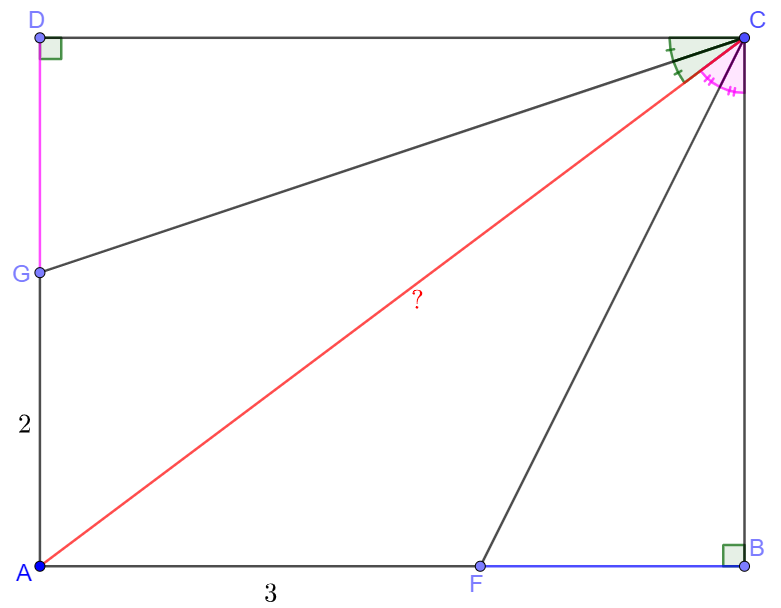
Solve:
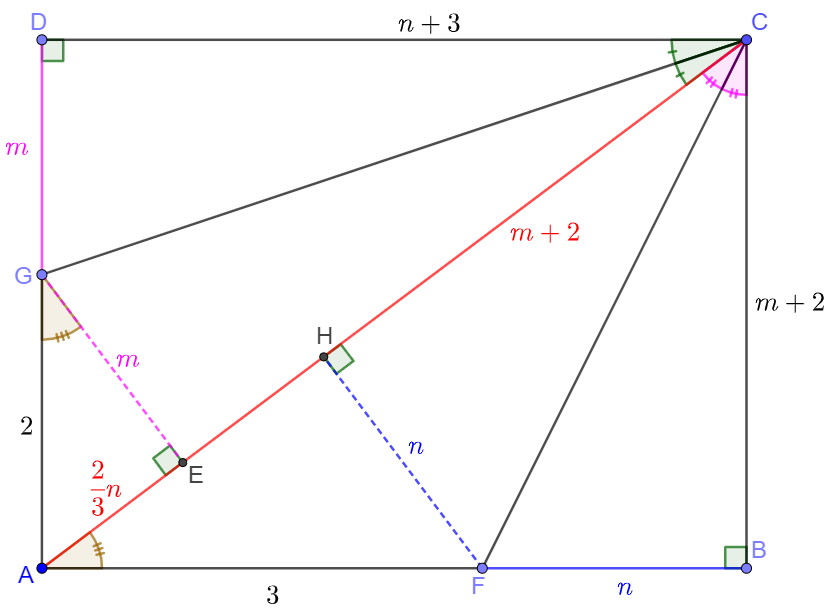
Make $DG \perp AC, FH \perp AC$, Let $DG=m, BF=n \implies EG=DG=m, BF=FH=n, CD=CG=n+3, BC=HC=m+2$
$\implies \angle{EGA}=\angle{HAF} \implies \dfrac{m}{2}=\dfrac{AH}{3} \implies AH=\dfrac{3}{2}m, AE=\dfrac{2}{3}n \implies AC=m+2+\dfrac{3}{2}m=n+3+\dfrac{2}{3}n \implies m=\dfrac{2}{5}+\dfrac{2}{3}n$
$EG^2+AE^2=AG^2 \implies m^2+\dfrac{4}{9}n^2=4 \implies \left( \dfrac{2}{5}+\dfrac{2}{3}n \right) ^2+\dfrac{4}{9}n^2=4 \implies \dfrac{1}{9}n^2+\dfrac{1}{15}n-\dfrac{12}{15}=0 \implies \left(\dfrac{1}{3}n-\dfrac{3}{5}\right) \left(\dfrac{1}{3}n+\dfrac{4}{5} \right)=0$
$\implies \dfrac{1}{3}n-\dfrac{3}{5}=0 \implies n=\dfrac{9}{5} \implies AC=3+\dfrac{5}{3}n=\bbox[1px, border: 1px solid black]{6}$
11/22/2021
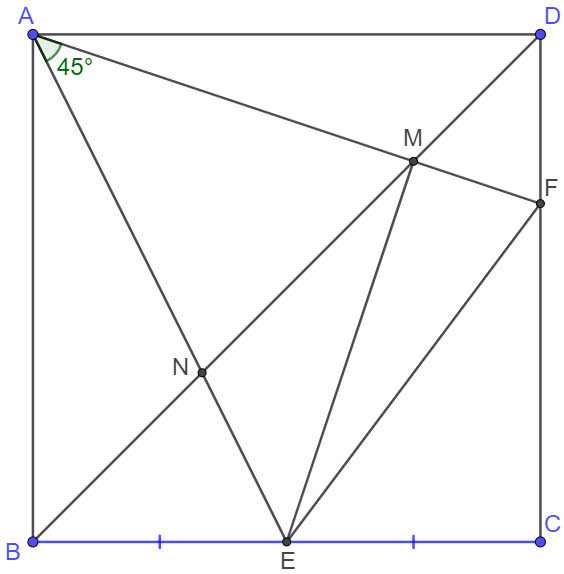
$E$ is midpoint on side of square $ABCD$ and $F$ is a point on side $CD$ so that $\angle{EAF}=45^{\circ}$. $AF$ and $BD$ intersects at $M$. Find $\dfrac{DF}{CF}$ and prove $EM\perp AF$.
Solve:
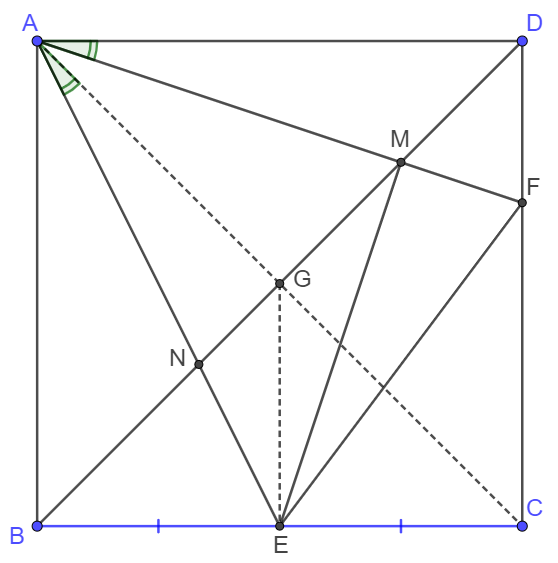
Connect $AC$ and intersects $BD$ at $G$. Connect $EG$. $\triangle{ABN} \sim \triangle{NGE} \implies \dfrac{NG}{BN}=\dfrac{EG}{AB}=\dfrac{1}{2}$
$\angle{EAF}=\angle{EAC}+\angle{CAF}=\angle{CAF}+\angle{FAD}=45^{\circ} \implies \angle{EAC}=\angle{FAD} \implies \triangle{ANG} \sim \triangle{AFD}$
$\triangle{AGB} \sim \triangle{ADC}, \triangle{ANG} \sim \triangle{AFD} \implies \dfrac{DF}{FC}=\dfrac{NG}{BN}=\bbox[1px, border: 1px solid black]{\dfrac{1}{2}}$
Prove:
$\angle{EBM}=\angle{EAM}=45^{\circ} \implies ABEM \text{ are cyclic } \implies \angle{AME}=180^{\circ}-\angle{ABE}=90^{\circ} \implies AM \perp ME \blacksquare$
11/23/2021
$\triangle{ABC}$ has $AB=AC=12, \angle{B}=30^{\circ}$, fold it along $EF$ so $B$ overlaps with the midpoint of $AC$ at $D$. Find the area of $\triangle{DEF}$
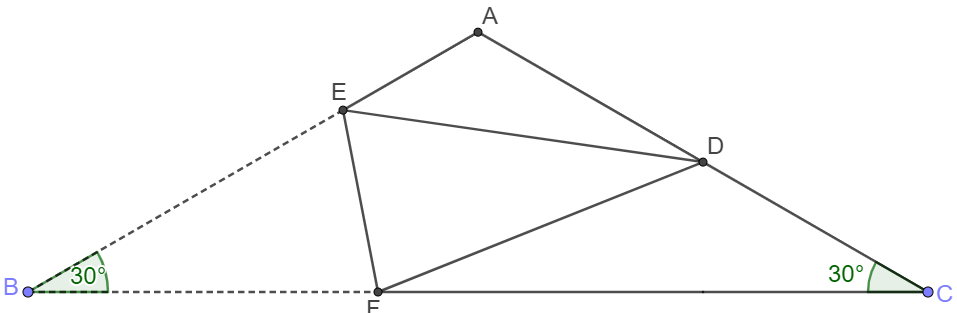
Solve:
Connect $BD$ and $EF$ intersects with it at $H$. Make $DM \perp AB$ at $M$, $DG \perp BC$ at $G$. Let $AE=a, DE=b$
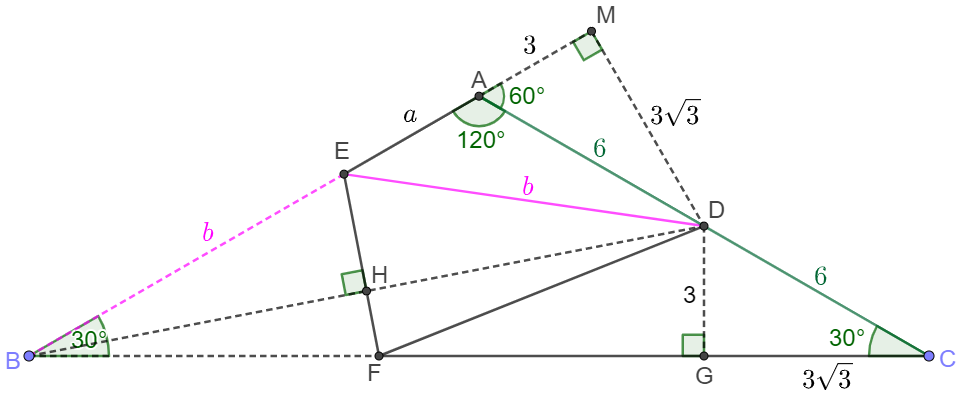
Easy to see $AM=DG=3, DM=CG=3\sqrt{3}, BC=12\sqrt{3} \implies BG=9\sqrt{3} \implies BD=6\sqrt{7} \implies BH=3\sqrt{7}$
$\dfrac{BH}{BE}=\dfrac{3\sqrt{7}}{b}=\dfrac{BM}{BD}=\dfrac{12+3}{6\sqrt{7}} \implies b=\dfrac{42}{5} \implies \dfrac{S_{\triangle{BDE}}}{S_{\triangle{ABD}}}=\dfrac{b}{12}=\dfrac{7}{10}$
$\dfrac{BH}{BF}=\dfrac{3\sqrt{7}}{BF}=\dfrac{BG}{BD}=\dfrac{9\sqrt{3}}{6\sqrt{7}} \implies BF=\dfrac{14\sqrt{3}}{3}\implies \dfrac{S_{\triangle{BDF}}}{S_{\triangle{BCD}}}=\dfrac{BF}{BC}=\dfrac{7}{18}$
$\implies S_{\triangle{DEF}}= \dfrac{S_{\triangle{BDE}}+S_{\triangle{BDF}}}{2}=\dfrac{(\dfrac{7}{10}+\dfrac{7}{18})S_{\triangle{ABC}}}{4}=\bbox[1px, border: 1px solid black]{\dfrac{49\sqrt{3}}{5}}$
11/24/2021
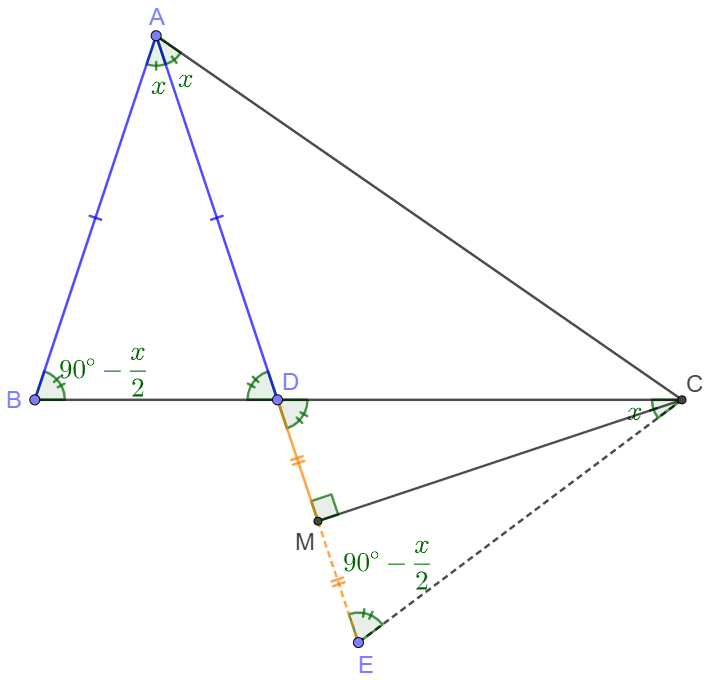
$\angle{BAD}=\angle{DAC}, AB=AD, CM \perp AM$ in $\triangle{ABC}$, prove $AM=\dfrac{AB+AC}{2}$
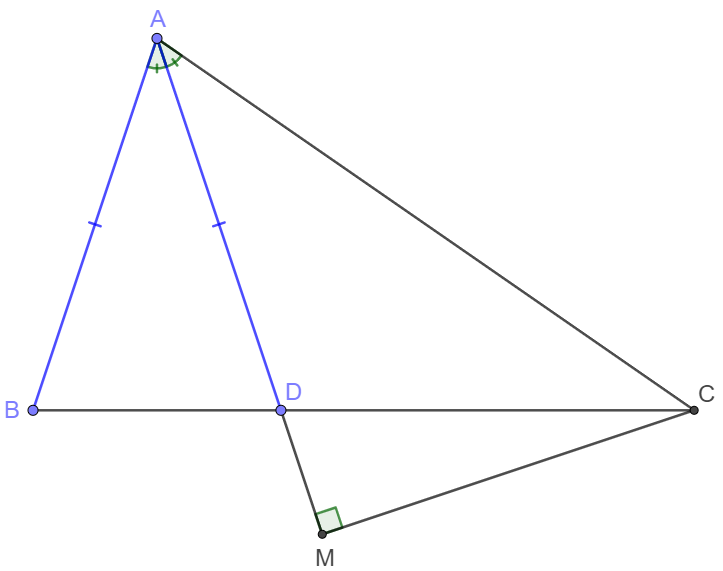
Prove:
Extend $DM$ to $E$ so that $DM=ME$, let $\angle{BAD}=x$,
easy to see $\angle{B}=90^{\circ}-\dfrac{x}{2}=\angle{ADB}=\angle{CDE}=\angle{DEC} \implies \angle{DCE}=x$
$\implies \angle{ACB}=180^{\circ}-2x-(90^{\circ}-\dfrac{x}{2})=90^{\circ}-\dfrac{3x}{2} $
$\implies \angle{ACE}=90^{\circ}-\dfrac{3x}{2}+x=90^{\circ}-\dfrac{x}{2}=\angle{DEC} \implies AE=AC$
$\implies AD+2DM=AC \implies AB+2DM=AC \implies \dfrac{AB}{2}+DM=\dfrac{AC}{2} $
$\implies AB+DM=\dfrac{AB+AC}{2} \implies AD+DM=AM=\dfrac{AB+AC}{2}\blacksquare$
11/25/2021
$\triangle{ABC}$ is an equilateral triangle with side length $6$. $E$ is on extended $BC$ and $\angle{AEB}=42^{\circ}$. $D$ is on $AE$ and $CD$ bisects $\angle{BDE}$. Find $CD$.
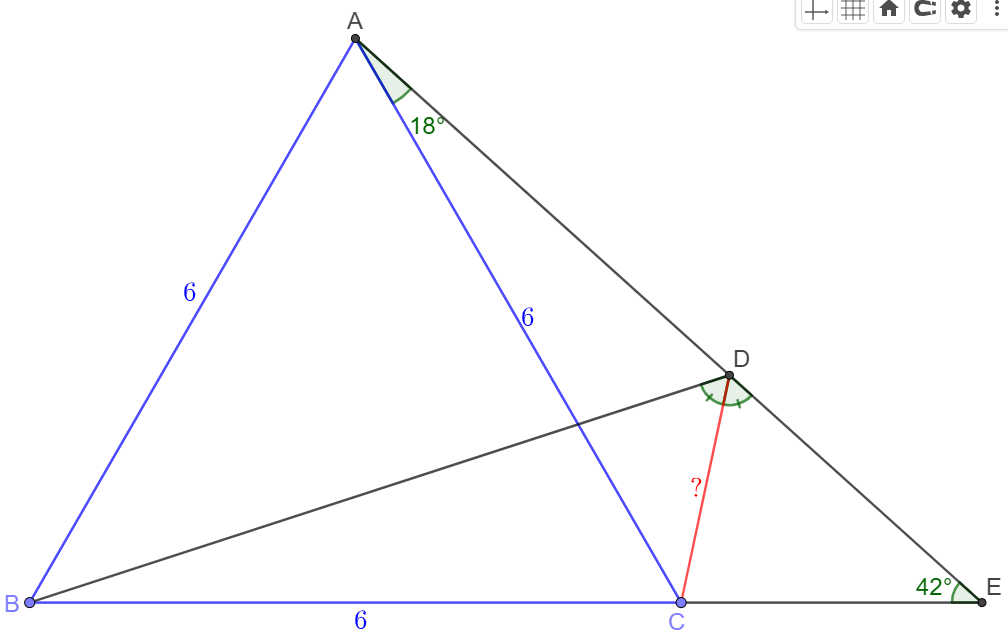
Solve:
From $C$ make $CK\perp BD, CL\perp DE$. Let $O$ be the circumcenter of $\triangle{ABC}$, connect $OD$.
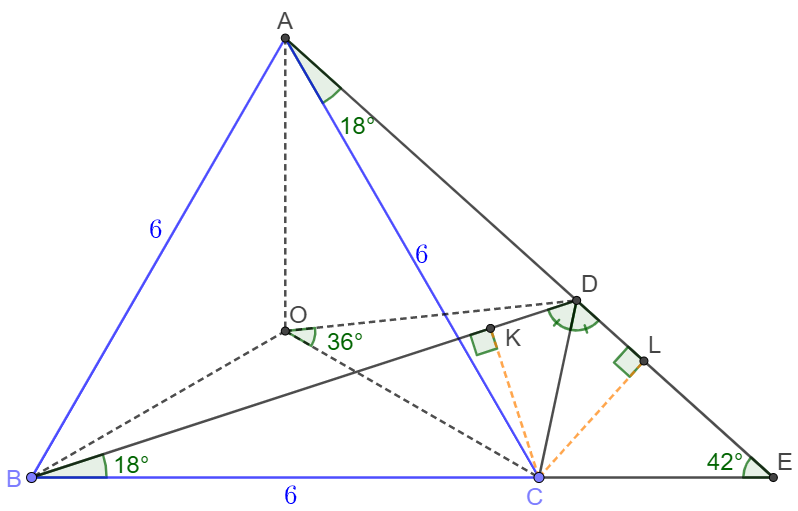
$CD$ bisects $\angle{BDE} \implies CK=CL$, and $BC=AC \implies \triangle{BCK} \cong \triangle{ACL} \implies \angle{CBD}=\angle{CAD}=60^{\circ}-42^{\circ}=18^{\circ}$
$ \implies \text{ABCD are cyclic} \implies \angle{COD} = 2 * 18^{\circ} = 36^{\circ} $ $\implies CD = \dfrac{2 * OC}{\sqrt{5} + 1} = \dfrac{2AC}{\sqrt{3}(\sqrt{5} + 1)} = \dfrac{2 * 6}{\sqrt{3}(\sqrt{5} + 1)} = \bbox[1px, border: 1px solid black]{\sqrt{15} - \sqrt{3}}$
11/26/2021
Solve $\displaystyle\int{\dfrac{1}{x^4+1}}\,dx$
Solve:
$\displaystyle \int \dfrac{1}{x^4+1}dx = \int \dfrac{\dfrac{1}{x^2}}{x^2+\dfrac{1}{x^2}}dx = \dfrac{1}{2} \int \dfrac{1+\dfrac{1}{x^2}-(1-\dfrac{1}{x^2})}{x^2+\dfrac{1}{x^2}} dx$
$\displaystyle =\dfrac{1}{2} \int\dfrac{d(x-\dfrac{1}{x})}{(x-\dfrac{1}{x})^2+2}-\dfrac{1}{2} \int \dfrac{d(x+\dfrac{1}{x})}{(x+\dfrac{1}{x})^2-2}$
$=\dfrac{1}{2\sqrt{2}} tan^{-1}\large ( \frac{x-\frac{1}{x}}{\sqrt{2}} \large )-\frac{1}{4\sqrt{2}}ln \left\lvert \frac{x+\frac{1}{x}-\sqrt{2}}{x+\frac{1}{x}+\sqrt{2}} \right\lvert + C$
$=\bbox[15px, border: 2px solid black] {\dfrac{1}{4\sqrt{2}} \Big[2 tan^{-1} \Big ( \dfrac{x^2-1}{\sqrt{2}x} \Big ) +ln \left\lvert \dfrac{x^2+\sqrt{2}x+1}{x^2-\sqrt{2}x+1} \right\lvert \Big] + C}$
11/27/2021
Solve $\displaystyle \lim_{d\to 0}{\dfrac{tan(d)-d}{d^3}}$
Solve 1:
$\displaystyle \lim_{d\to 0}{\dfrac{tan(d)-d}{d^3}}=\lim_{d\to 0}\dfrac{sec^2(d)-1}{3d^2}=\lim_{d\to 0}\dfrac{1-cos(d)}{3d^2} \cdot \dfrac{1+cos(d)}{cos^2(d)}=2\lim_{d\to 0}\dfrac{sin(d)}{6d}=\dfrac{2}{6}=\bbox[1px, border: 1px solid black]{\dfrac{1}{3}}$
Solve 2:
$\displaystyle K=\lim_{d\to 0}{\dfrac{tan(d)-d}{d^3}}=\lim_{t \to 0}{\dfrac{tan(2t)-2t}{8t^3}}=\dfrac{1}{4}\lim_{t \to 0}{\dfrac{\dfrac{1}{2}tan(2t)-t}{x^3}}$
$=\displaystyle \dfrac{1}{4}\Big (\lim_{t \to 0}\dfrac{\dfrac{1}{2}tan(2t)-t-(tan(t)-t)}{t^3} + \lim_{t\to 0}{\dfrac{tan(t)-t}{t^3}} \Big)$
$=\displaystyle \dfrac{1}{4} \Big( \lim_{t\to 0}{\dfrac{\dfrac{tan(t)}{1-tan^2(t)}-tan(t)}{t^3}} + K \Big)=\dfrac{1}{4} \Big( \lim_{t\to 0}{\dfrac{tan^3(t)}{t^3}} + K \Big)=\dfrac{1}{4} \Big(1+K \Big)\implies K=\bbox[1px, border: 1px solid black]{\dfrac{1}{3}}$