October 2021

10/21/2021

$\angle{B}=80^{\circ}$ in $\triangle{ABC}$ and $BD$ is angle bisector which makes $AD=BC+BD$. Find $\angle{A}$.

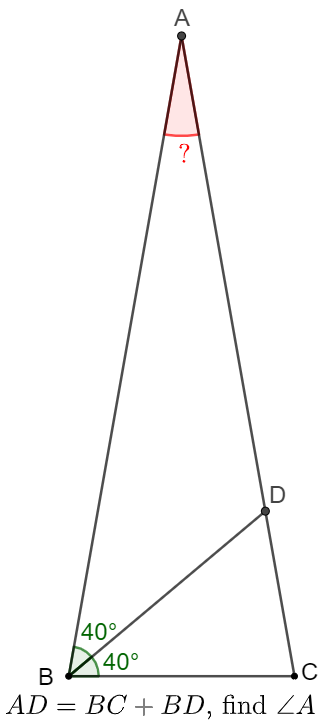
Solve 1:

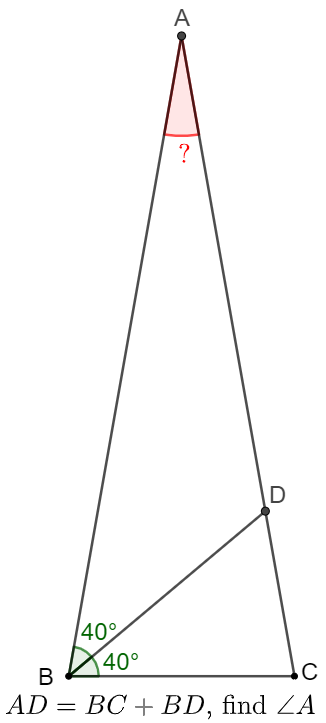
(Chinese Version: )

$AD=BC+BD \gt BD \implies \angle{A} < \angle{ABD} \implies \angle{A} \lt 40^{\circ}$。令 $\angle{A}=\alpha \in (0， 40^{\circ})$。

$\dfrac{AD}{BD}=\dfrac{sin(40^{\circ})}{sin(\alpha)}=\dfrac{BC+BD}{BD}=1+\dfrac{BC}{BD}=1+\dfrac{sin(\angle{BDC})}{sin(\angle{C})}=1+\dfrac{sin(\alpha+40^{\circ})}{sin(\alpha+80^{\circ})}$

$=\dfrac{sin(\alpha+80^{\circ})+sin(\alpha+40^{\circ})}{sin(\alpha+80^{\circ})}=\dfrac{2sin(\alpha+60^{\circ})cos(20^{\circ})}{sin(\alpha+80^{\circ})} \implies sin(\alpha)sin(\alpha+60^{\circ})=sin(\alpha+80^{\circ})sin(20^{\circ})$

令$f(\alpha)=sin(\alpha)sin(\alpha+60^{\circ})-sin(\alpha+80^{\circ})sin(20^{\circ})$, 显见 $f(20^{\circ})=0$ 且

$f’(\alpha)=cos(\alpha)sin(\alpha+60^{\circ})+sin(\alpha)cos(\alpha+60^{\circ})-sin(20^{\circ})cos(\alpha+80^{\circ})=sin(2\alpha+60^{\circ})-sin(20^{\circ})cos(\alpha+80^{\circ})$

$\alpha \in (0， 40^{\circ}) \implies sin(2\alpha+60^{\circ}) \gt sin(40^{\circ}) \gt sin(20^{\circ})cos(\alpha+80^{\circ}) \implies f ‘(\alpha) \gt 0 \implies \angle{A}=\bbox[1px, border: 1px solid black]{20^{\circ}}$为唯一解。

(English Verison: )

$AD=BC+BD \gt BD \implies \angle{A} < \angle{ABD} \implies \angle{A} \lt 40^{\circ}$. Let $\angle{A}=\alpha \in (0， 40^{\circ})$。

$\dfrac{AD}{BD}=\dfrac{sin(40^{\circ})}{sin(\alpha)}=\dfrac{BC+BD}{BD}=1+\dfrac{BC}{BD}=1+\dfrac{sin(\angle{BDC})}{sin(\angle{C})}=1+\dfrac{sin(\alpha+40^{\circ})}{sin(\alpha+80^{\circ})}$

Let $f(\alpha)=sin(\alpha)sin(\alpha+60^{\circ})-sin(\alpha+80^{\circ})sin(20^{\circ})$, obviously $f(20^{\circ})=0$ and

$f’(\alpha)=cos(\alpha)sin(\alpha+60^{\circ})+sin(\alpha)cos(\alpha+60^{\circ})-sin(20^{\circ})cos(\alpha+80^{\circ})=sin(2\alpha+60^{\circ})-sin(20^{\circ})cos(\alpha+80^{\circ})$

Solve 2:

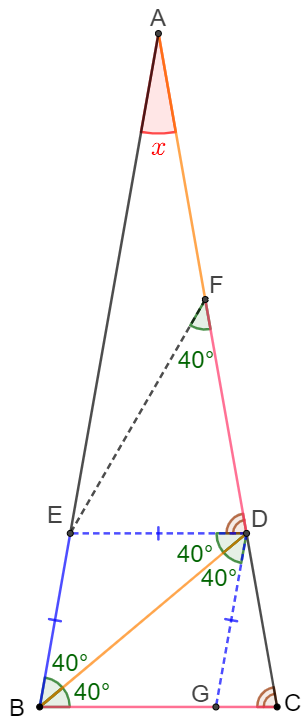
(Chinese Version):

$AB$上取$E$使得$DE \parallel BC$, $BC$上取$G$使得$DG \parallel AB$, $AD$上取$F$使得$\angle{EFD}=40^{\circ}$。

$DE \parallel BC, DG \parallel AB \implies \angle{EDB}=\angle{CBD}=40^{\circ}=\angle{DBE}=\angle{BDG} \implies BE=DE=DG$

$DE \parallel BC \implies \angle{FDE}=\angle{DCB}$, 且 $\angle{CBD}=\angle{EFD}=40^{\circ} \implies \triangle{DEF} \sim \triangle{CDB}$

比较 $CD$ 与 $BE$. 共三种可能性：

1) 假设 $CD=BE \implies CD=DG \implies \angle{C}=\angle{DGC}=\angle{EBC}=80^{\circ}\implies \angle{A}=20^{\circ}$ 2) 假设 $CD \gt BE \implies CD \gt DG \implies \angle{C} < \angle{DGC} \implies \angle{C} \lt 80^{\circ} \implies \angle{A} \gt 20^{\circ}$ 由于$\angle{A}+\angle{AEF}=40^{\circ} \implies \angle{A}>\angle{AEF} \implies EF \gt AF$ $CD\gt BE \implies CD \gt DE$, 由于$\triangle{DEF} \sim \triangle{CDB}$, 易知 $BD \gt EF, BC \gt DF$ $BC \gt DF, AD=DF+AF=BC+BD \implies BD \lt AF \implies BD \lt EF$ 这样同时有 $BD \lt EF$ 以及 $BD \gt EF$ 矛盾，所以 $CD \gt BE$ 的假设不真。 3) 假设 $CD < BE$, 类似可知同样会推出矛盾，所以 $CD \lt BE$ 的假设不真。

从而只能 $CD=BE \implies \angle{C}=80^{\circ} \implies \angle{A}=\bbox[1px, border: 1px solid black]{20^{\circ}}$.

(English Version):

Let $E$ on side $AB$ and $DE \parallel BC$. Let $G$ on side $BC$ and $DG \parallel AB. $ Let $F$ on side $AC$ and $\angle{EFD}=40^{\circ}$.

$DE \parallel BC, DG \parallel AB \implies \angle{EDB}=\angle{CBD}=40^{\circ}=\angle{DBE}=\angle{BDG} \implies BE=DE=DG$

$DE \parallel BC \implies \angle{FDE}=\angle{DCB}$, and we have $\angle{CBD}=\angle{EFD}=40^{\circ} \implies \triangle{DEF} \sim \triangle{CDB}$

Compare $CD$ and $BE$. There are three possibilities:

1) If $CD=BE \implies CD=DG \implies \angle{C}=\angle{DGC}=\angle{EBC}=80^{\circ}\implies \angle{A}=20^{\circ}$ 2) If $CD \gt BE \implies CD \gt DG \implies \angle{C} < \angle{DGC} \implies \angle{C} \lt 80^{\circ} \implies \angle{A} \gt 20^{\circ}$ Since $\angle{A}+\angle{AEF}=40^{\circ} \implies \angle{A}>\angle{AEF} \implies EF \gt AF$ $CD\gt BE \implies CD \gt DE$, since $\triangle{DEF} \sim \triangle{CDB}$, we know $BD \gt EF, BC \gt DF$ $BC \gt DF, AD=DF+AF=BC+BD \implies BD \lt AF \implies BD \lt EF$ Thus we have $BD \lt EF$ and $BD \gt EF$ as contradiction, so we know $CD > BE$ is false. 3) If $CD < BE$, by similar deduction we can know this is false as well.

Then we know $CD=BE \implies \angle{C}=80^{\circ} \implies \angle{A}=\bbox[1px, border: 1px solid black]{20^{\circ}}$.

Solve 3 (via trigonometry):

From the Laws of Sines we know that

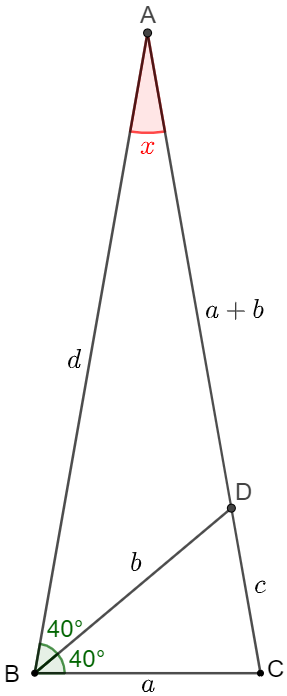
$\dfrac{AD}{sin(40^{\circ})}=\dfrac{AB}{sin(40^{\circ}+x)} \implies AD=\dfrac{sin(40^{\circ})}{sin(40^{\circ}+x)}AB,$

$\dfrac{BD}{sin(x)}=\dfrac{AB}{sin(40^{\circ}+x)} \implies BD=\dfrac{sin(x)}{sin(40^{\circ}+x)}AB, $

$\dfrac{BC}{sin(x)}=\dfrac{AB}{sin(80^{\circ}+x)} \implies BC=\dfrac{sin(x)}{sin(80^{\circ}+x)}AB$

$AD=BC+BD \implies \dfrac{sin(40^{\circ})}{sin(40^{\circ}+x)}=\dfrac{sin(x)}{sin(40^{\circ}+x)}+\dfrac{sin(x)}{sin(80^{\circ}+x)}$

$\implies sin(40^{\circ})sin(80^{\circ}+x)-sin(x)sin(80^{\circ}+x)=sin(x)sin(40^{\circ}+x)$

Use $sin(A)sin(B)=-\dfrac{1}{2}(cos(A+B)-cos(A-B))$, we get $[cos(120^{\circ}+x)-cos(40^{\circ}+x)]-[cos(80^{\circ}+2x)-cos(80^{\circ})]=cos(40^{\circ}+2x)-cos(40^{\circ})$

$\implies cos(80^{\circ}+2x)-cos(80^{\circ})+cos(60^{\circ}-x)+cos(40^{\circ}+x)=cos(40^{\circ})-cos(40^{\circ}+2x)$

$\implies cos(80^{\circ}+2x)+cos(40^{\circ}+2x)+cos(60^{\circ}-x)+cos(40^{\circ}+x)=cos(40^{\circ})+cos(80^{\circ})$

Use $cos(A)+cos(B)=2cos(\dfrac{A+B}{2})cos(\dfrac{A-B}{2})$, we get

$2cos(60^{\circ}+2x)cos(20^{\circ})+2cos(50^{\circ})cos(10^{\circ}-x)=2cos(60^{\circ})cos(20^{\circ})$

$\implies cos(50^{\circ})cos(10^{\circ}-x)=cos(20^{\circ})[cos(60^{\circ})-cos(60^{\circ}+2x)]$

Use $cos(A)-cos(B)=-2sin(\dfrac{A+B}{2})sin(\dfrac{A-B}{2})$, we get

$cos(50^{\circ})cos(10^{\circ}-x)=2cos(20^{\circ})sin(60^{\circ}+x)sin(x)$

$\implies sin(40^{\circ})sin(80^{\circ}+x)=2sin(20^{\circ})cos(20^{\circ})sin(100^{\circ}-x)=2cos(20^{\circ})sin(60^{\circ}+x)sin(x)$

$\implies sin(20^{\circ})sin(100^{\circ}-x)=sin(60^{\circ}+x)sin(x)$

By observation, $x=20^{\circ}$. This is from original approach. Not strict step here.

Unsolved Approach:

Let $BC=a, AB=d, CD=c, BD=b$, then $AD=a+b$

$\dfrac{a}{c}=\dfrac{d}{a+b} \implies d=\dfrac{a(a+b)}{c} \implies ad=\dfrac{a^2(a+b)}{c}, a+d=\dfrac{a(a+b+c)}{c}$

And we know from the length of angle sector that $b^2=ad-\dfrac{(a+b+c)^2ad}{(a+d)^2}=\dfrac{a^2(a+b)}{c}-\dfrac{(a+b+c)^2\dfrac{a^2(a+b)}{c}}{\dfrac{a^2(a+b+c)^2}{c^2}}=\dfrac{a^2(a+b)}{c}-c(a+b)=\dfrac{(a^2-c^2)(a+b)}{c}$

$\implies cos(\angle{BDC})=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{c^2-a^2+\dfrac{(a^2-c^2)(a+b)}{c}}{2bc}=\dfrac{(a^2-c^2)(a+b-c)}{2bc^2}$

From Laws of Sines we know $\dfrac{d}{sin(\angle{C})}=\dfrac{a+b+c}{sin80^{\circ}} \implies \dfrac{a(a+b)}{csin(\angle{C})}=\dfrac{a+b+C}{sin80^{\circ}} \implies sin(\angle{C})=\dfrac{a(a+b)sin80^{\circ}}{c(a+b+c)}$

and we also know $\dfrac{b}{sin(\angle{C})}=\dfrac{c}{sin40^{\circ}}\implies \dfrac{bc(a+b+c)}{a(a+b)sin80^{\circ}}=\dfrac{c}{sin40^{\circ}} \implies \dfrac{b(a+b+c)}{2a(a+b)sin40^{\circ}cos40^{\circ}}=\dfrac{1}{sin40^{\circ}}$

$\implies cos40^{\circ}=\dfrac{b(a+b+c)}{2a(a+b)}=\dfrac{a^2+b^2-c^2}{2ab} \implies \dfrac{b^2(a+b+c)}{a+b}=a^2+b^2-c^2 \implies b^2+\dfrac{b^2c}{a+b}=a^2+b^2-c^2$

$\implies a^2-c^2=\dfrac{b^2c}{a+b} \implies cos(\angle{BDC})=\dfrac{(a^2-c^2)(a+b-c)}{2bc^2} = \dfrac{\dfrac{b^2c}{a+b}(a+b-c)}{2bc^2}=\dfrac{b(a+b-c)}{2c(a+b)}=\dfrac{b-\dfrac{bc}{a+b}}{2c}$

if $cos(\angle{BDC})=\dfrac{1}{2} \implies b-c=\dfrac{bc}{a+b}$

10/22/2021

How many distinct permutations from $1,1,2,2,3,3,4,4$ that there are no equal consecutive numbers?

Solve:

Calculate all distinct permutations of $1,1,2,2,3,3,4,4$. The generate function for all distinct permutations of $1,1,2,2,3,3,4,4$ is $g(x)=(1+x+\dfrac{x^2}{2!})^4$ , its coefficient of $x^8$ in $g(x)$ is $\dfrac{1}{16}$, so the number of total distinct permutations is $\dfrac{1}{16}*8!=2520$.
Calculate all distinct permutations of $1,1,2,2,3,3,4,4$ that contains $1$ pair of equal consecutive numbers. There are $4 \choose 1$ ways to choose the equal consecutive number, and take it as one number to permute with other $6$ numbers, so the generate function is $(1+x)(1+x+\dfrac{x^2}{2!})^3$, its coefficient of $x^7$ is $\dfrac{1}{8}$, so the number of distinct permutations is $4 * \dfrac{1}{8} * 7! = 2520$.
Calculate all distinct permutations of $1,1,2,2,3,3,4,4$ that contains $2$ pairs of equal consecutive numbers. There are $4 \choose 2$ ways to choose the equal consecutive numbers and take each of them as one number to permute with other 4 numbers, so the generate function is $(1+x)^2(1+x+\dfrac{x^2}{2})^2$, its coefficient of $x^6$ is $\dfrac{1}{4}$, so the number of distinct permutations is ${4 \choose 2} * \dfrac{1}{4} * 6!=1080$.
Calculate all distinct permutations of $1,1,2,2,3,3,4,4$ that contains $3$ pairs of equal consecutive numbers. There are $4 \choose 3$ ways to choose the equal consecutive numbers and take each of them as one number to permute with the rest 2 numbers, so the generate function is $(1+x)^3(1+x+\dfrac{x^2}{2})$, its coefficient of $x^5$ is $\dfrac{1}{2}$, so the number of distinct permutations is ${4 \choose 3} * \dfrac{1}{2} * 5!=240$.
Calculate all distinct permutations of $1,1,2,2,3,3,4,4$ that contains $4$ pairs of equal consecutive numbers. Take each of pair of them as one number, so this is permutation of 4 numbers: $4!=24$.

According to PIE, the result is $2520-2520+1080-240+24=\bbox[1px, border: 1px solid black]{864}$.

PREVIOUSSeptember 2021

NEXTElements of Abstract Algebra Notes